qt widget和qml界面集成到一起
相关文章:

qt widget和qml界面集成到一起
将 Qt Widgets 和 QML 界面集成在一起可以利用 QQuickWidget 或 QQuickView。以下是基本步骤: 使用 QQuickWidget 创建 Qt Widgets 项目: 创建一个基于 Widgets 的应用程序。添加 QQuickWidget: 在你的窗口或布局中添加 QQuickWidget。 例如,可以在 QMainWindow 中使用: …...
BUU30 [网鼎杯 2018]Fakebook1
是一个登录界面,我们先注册一个试试: 用dirsearch扫描出来robots.txt,也发现了flag.php,并下载user.php.bak 源代码内容: <?phpclass UserInfo {public $name "";public $age 0;public $blog &quo…...
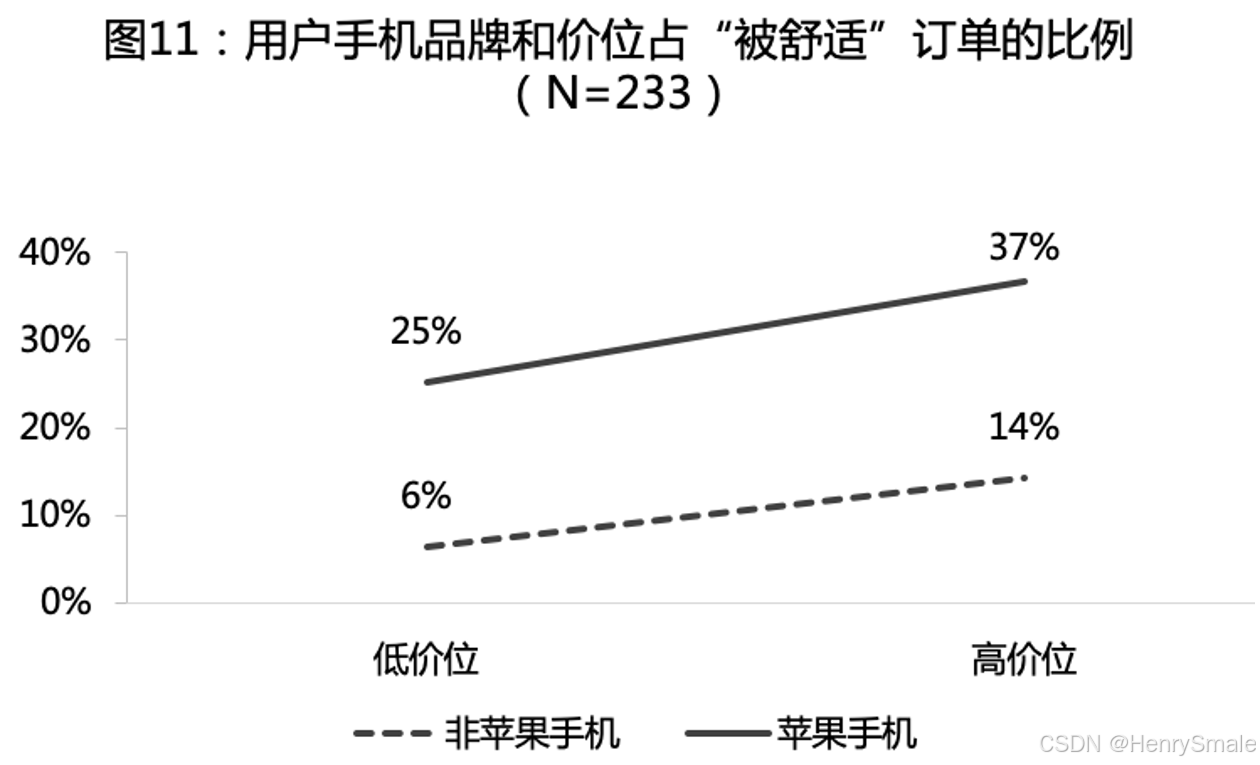
信息科技伦理与道德3-2:智能决策
2.2 智能推荐 推荐算法介绍 推荐系统:猜你喜欢 https://blog.csdn.net/search_129_hr/article/details/120468187 推荐系统–矩阵分解 https://blog.csdn.net/search_129_hr/article/details/121598087 案例一:YouTube推荐算法向儿童推荐不适宜视频 …...

《代码随想录第二十八天》——回溯算法理论基础、组合问题、组合总和III、电话号码的字母组合
《代码随想录第二十八天》——回溯算法理论基础、组合问题、组合总和III、电话号码的字母组合 本篇文章的所有内容仅基于C撰写。 1. 基础知识 1.1 概念 回溯是递归的副产品,它也是遍历树的一种方式,其本质是穷举。它并不高效,但是比暴力循…...

PromptSource官方文档翻译
目录 核心概念解析 提示模板(Prompt Template) P3数据集 安装指南 基础安装(仅使用提示) 开发环境安装(需创建提示) API使用详解 基本用法 子数据集处理 批量操作 提示创建流程 Web界面操作 手…...

USB子系统学习(四)用户态下使用libusb读取鼠标数据
文章目录 1、声明2、HID协议2.1、描述符2.2、鼠标数据格式 3、应用程序4、编译应用程序5、测试6、其它 1、声明 本文是在学习韦东山《驱动大全》USB子系统时,为梳理知识点和自己回看而记录,全部内容高度复制粘贴。 韦老师的《驱动大全》:商…...

Ansible简单介绍及用法
一、简介 Ansible是一个简单的自动化运维管理工具,基于Python语言实现,由Paramiko和PyYAML两个关键模块构建,可用于自动化部署应用、配置、编排task(持续交付、无宕机更新等)。主版本大概每2个月发布一次。 Ansible与Saltstack最大的区别是…...

目前推荐的优秀编程学习网站与资源平台,涵盖不同学习方式和受众需求
一、综合教程与互动学习平台 菜鸟教程 特点:适合零基础新手,提供免费编程语言教程(Python、Java、C/C++、前端等),页面简洁且包含大量代码示例,支持快速上手。适用人群:编程入门者、需要快速查阅语法基础的学习者。W3Schools 特点:专注于Web开发技术(HTML、CSS、JavaS…...
)
软件工程-软件需求规格说明(SRS)
基本介绍 目标 便于用户、分析人员、设计人员进行交流 支持目标软件系统的确认(验收) 控制系统进化过程(追加需求):拥有版本记录表 需要在软件分析完成后,编写完成软件需求说明书。 具体标准可参考GB…...

运维_Mac环境单体服务Docker部署实战手册
Docker部署 本小节,讲解如何将前端 后端项目,使用 Docker 容器,部署到 dev 开发环境下的一台 Mac 电脑上。 1 环境准备 需要安装如下环境: Docker:容器MySQL:数据库Redis:缓存Nginx&#x…...

UE5.5 PCGFrameWork--GPU CustomHLSL
在上一篇UE5.5 PCGFrameWork使用入门-CSDN博客 大致介绍了UE5 PCG框架的基本使用. 本篇探索PCGFrame的高级应用--GPU点云。也就是利用GPU HLSL编程对点云进行操纵,可以大幅度提升点云生成效率。 目前在UE5 PCG框架中,点云GPU的应用大致分为三类: Point…...

RabbitMQ 如何设置限流?
RabbitMQ 的限流(流量控制)主要依赖于 QoS(Quality of Service) 机制,即 prefetch count 参数。这个参数控制每个消费者一次最多能获取多少条未确认的消息,从而避免某个消费者被大量消息压垮。 1. RabbitMQ…...

json格式,curl命令,及轻量化处理工具
一. JSON格式 JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式。它基于一个子集的JavaScript编程语言,使用人类易于阅读的文本格式来存储和表示数据。尽管名字中有“JavaScript”,但JSON是语言无关的,几…...

Postman面试问题
在 API 测试领域,Postman 已成为最流行的工具之一。无论是功能测试、自动化测试,还是接口调试,Postman 都扮演着重要角色。而在软件测试面试中,Postman 相关问题更是高频考点。如果你正在准备面试,赶紧看看这些Postman…...

【JVM详解四】执行引擎
一、概述 Java程序运行时,JVM会加载.class字节码文件,但是字节码并不能直接运行在操作系统之上,而JVM中的执行引擎就是负责将字节码转化为对应平台的机器码让CPU运行的组件。 执行引擎是JVM核心的组成部分之一。可以把JVM架构分成三部分&am…...

esp32 udp 客户端 广播
esp32 udp 客户端 广播 #include "bsp_udpc.h"// #include "com_config.h" // #include "com_xqueue.h"#include "bsp_udpc.h" #define TAG "bsp_udpc"#include <string.h> #include <sys/param.h> #include &q…...

nginx日志存储access日志和error保留180天,每晚把前一天的日志文件压缩成tar.gz
logrotate日志分割时,rotate参数是必须要加的 在logrotate的配置文件中,rotate参数用于指定保留的旧日志文件数量。如果不配置rotate参数,默认是0个,也就是只允许存在一份日志,刚切分出来的日志会马上被删除 l…...

【Java】多线程和高并发编程(四):阻塞队列(上)基础概念、ArrayBlockingQueue
文章目录 四、阻塞队列1、基础概念1.1 生产者消费者概念1.2 JUC阻塞队列的存取方法 2、ArrayBlockingQueue2.1 ArrayBlockingQueue的基本使用2.2 生产者方法实现原理2.2.1 ArrayBlockingQueue的常见属性2.2.2 add方法实现2.2.3 offer方法实现2.2.4 offer(time,unit)方法2.2.5 p…...
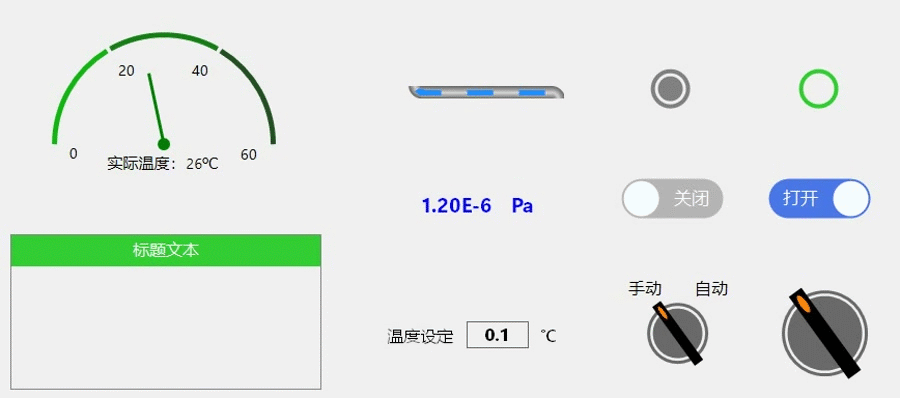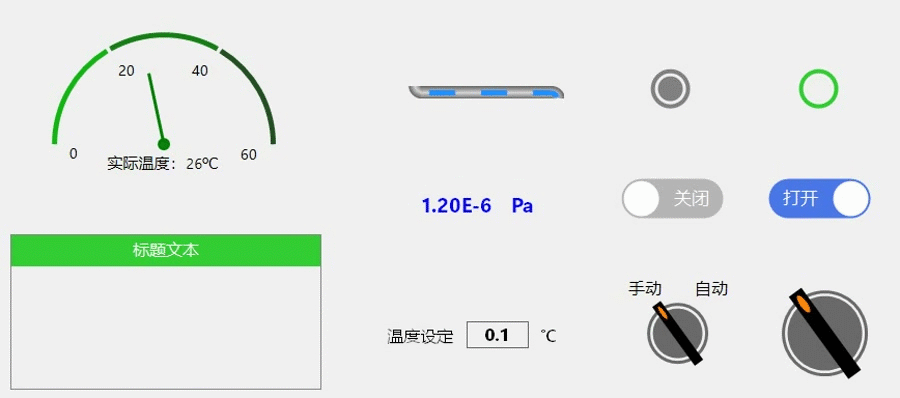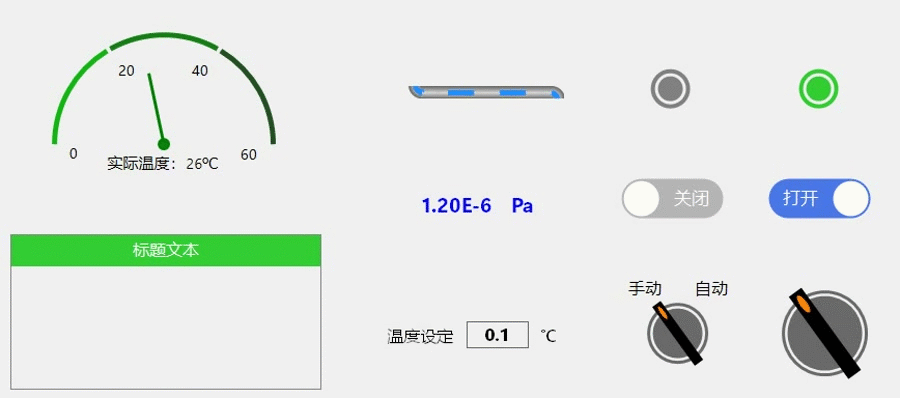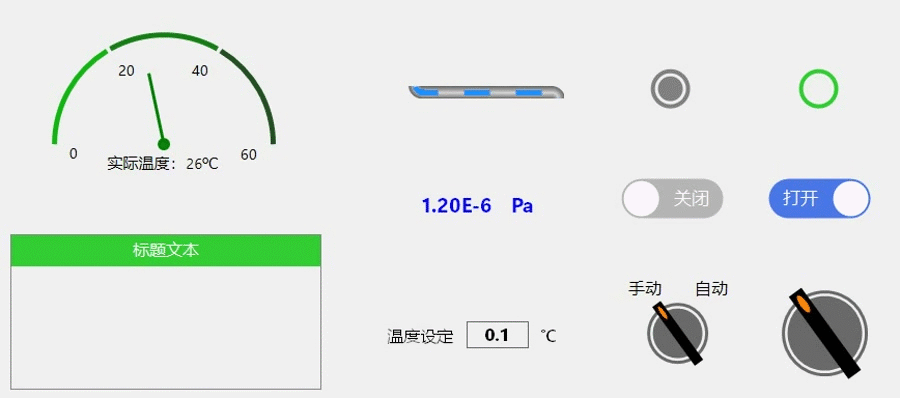
C#控件开发6—旋转按钮
按钮功能:手自动旋转,标签文本显示、点击二次弹框确认(源码在最后边); 【制作方法】 找到控件的中心坐标,画背景外环、内圆;再绘制矩形开关,进行角度旋转即可获得; 【关…...

在亚马逊云科技上云原生部署DeepSeek-R1模型(下)
在本系列的上篇中,我们介绍了如何通过Amazon Bedrock部署并测试使用了DeepSeek模型。在接下来的下篇中小李哥将继续介绍,如何利用亚马逊的AI模型训练平台SageMaker AI中的,Amazon Sagemaker JumpStart通过脚本轻松一键式部署DeepSeek预训练模…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
