【王道数据结构】第六章(下) | 图的应用
目录
一、最小生成树
二、最短路径
三、有向⽆环图描述表达式
四、拓扑排序
五、关键路径
一、最小生成树
1、最小生成树的概念
对于一个带权连通无向图G = (V,E),生成树不,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的最小生成树(Minimum-Spannino-Tree,MST).。
- 最小生成树可能有多个,但边的权值之和总是唯一且最小的。
- 最小生成树的边数 =顶点数 -1。砍掉一条则不连通,增加一条边则会出现回路。
- 如果一个连通图本身就是一棵树,则其最小生成树就是它本身。
- 只有连通图才有生成树,非连通图只有生成森林。
2、求最小生成树的两种方法
- Prim算法
- Kruskal算法
Prim算法(普里姆):从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。时间复杂度: O(V2)适合用于边稠密图
Kruskal算法(克鲁斯卡尔):每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。时间复杂度: O(lEllog2lEl )适合用于边稀疏图
二、最短路径
 1.无权图的单源最短路径问题——BFS算法
1.无权图的单源最短路径问题——BFS算法
使用 BFS算法求无权图的最短路径问题,需要使用三个数组
d[]数组用于记录顶点 u 到其他顶点的最短路径。path[]数组用于记录最短路径从那个顶点过来。visited[]数组用于记录是否被访问过。
代码时间
#define MAX_LENGTH 2147483647 //地图中最大距离,表示正无穷// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){for(i=0; i<G.vexnum; i++){visited[i]=FALSE; //初始化访问标记数组d[i]=MAX_LENGTH; //初始化路径长度path[i]=-1; //初始化最短路径记录}InitQueue(Q); //初始化辅助队列d[u]=0;visites[u]=TREE;EnQueue(Q,u);while(!isEmpty[Q]){ //BFS算法主过程DeQueue(Q,u); //队头元素出队并赋给ufor(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w)){if(!visited[w]){d[w]=d[u]+1;path[w]=u;visited[w]=TREE;EnQueue(Q,w); //顶点w入队}}}
}
2.单源最短路径问题——Dijkstra算法
- BFS算法的局限性:BFS算法求单源最短路径只适⽤于⽆权图,或所有边的权值都相同的图。
- Dijkstra算法能够很好的处理带权图的单源最短路径问题,但不适⽤于有负权值的带权图。
- 使用 Dijkstra算法求最短路径问题,需要使用三个数组:
final[]数组用于标记各顶点是否已找到最短路径。dist[]数组用于记录各顶点到源顶点的最短路径长度。path[]数组用于记录各顶点现在最短路径上的前驱。
代码实现
#define MAX_LENGTH = 2147483647;// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){for(int i=0; i<G.vexnum; i++){ //初始化数组final[i]=FALSE;dist[i]=G.edge[u][i];if(G.edge[u][i]==MAX_LENGTH || G.edge[u][i] == 0)path[i]=-1;elsepath[i]=u;final[u]=TREE;}for(int i=0; i<G.vexnum; i++){int MIN=MAX_LENGTH;int v;// 循环遍历所有结点,找到还没确定最短路径,且dist最⼩的顶点vfor(int j=0; j<G.vexnum; j++){if(final[j]!=TREE && dist[j]<MIN){MIN = dist[j];v = j;}}final[v]=TREE;// 检查所有邻接⾃v的顶点路径长度是否最短for(int j=0; j<G.vexnum; j++){if(final[j]!=TREE && dist[j]>dist[v]+G.edge[v][j]){dist[j] = dist[v]+G.edge[v][j];path[j] = v;}}}
}
3.各顶点间的最短路径问题——Floyd算法
-
Floyd算法:求出每⼀对顶点之间的最短路径,使⽤动态规划思想,将问题的求解分为多个阶段。
-
Floyd算法可以⽤于负权值带权图,但是不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径。
-
Floyd算法使用到两个矩阵:
dist[][]:目前各顶点间的最短路径。path[][]:两个顶点之间的中转点。
-
代码实现:
int dist[MaxVertexNum][MaxVertexNum];
int path[MaxVertexNum][MaxVertexNum];void Floyd(MGraph G){int i,j,k;// 初始化部分for(i=0;i<G.vexnum;i++){for(j=0;j<G.vexnum;j++){dist[i][j]=G.Edge[i][j]; path[i][j]=-1;}}// 算法核心部分for(k=0;k<G.vexnum;k++){for(i=0;i<G.vexnum;i++){for(j=0;j<G.vexnum;j++){if(dist[i][j]>dist[i][k]+dist[k][j]){dist[i][j]=dist[i][k]+dist[k][j];path[i][j]=k;}}}}
}
4.最短路径算法比较:
| BFS算法 | Dijkstra算法 | Floyd算法 | |
|---|---|---|---|
| 无权图 | ✔ | ✔ | ✔ |
| 带权图 | ✘ | ✔ | ✔ |
| 带负权值的图 | ✘ | ✘ | ✔ |
| 带负权回路的图 | ✘ | ✘ | ✘ |
| 时间复杂度 | O(|V|^2)或(|V|+|E|) | O(|V|^2) | O(|V|^3) |
| 通常⽤于 | 求⽆权图的单源最短路径 | 求带权图的单源最短路径 | 求带权图中各顶点间的最短路径 |
三、有向⽆环图描述表达式
1.有向⽆环图:若⼀个有向图中不存在环,则称为有向⽆环图,简称 DAG图(Directed Acyclic Graph)。
DAG描述表达式:((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)
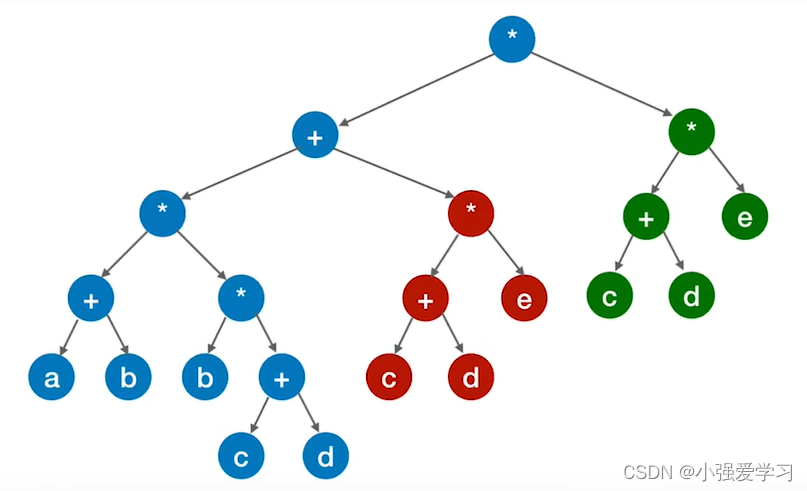
2.有向无环图描述表达式的解题步骤:
- Step 1:把各个操作数不重复地排成一排
- Step 2:标出各个运算符的生效顺序 (先后顺序有点出入无所谓)
- Step 3:按顺序加入运算符,注意“分层”
- Step 4:从底向上逐层检查同层的运算符是否可以合体
四、拓扑排序
1.AOV网(Activity on Vertex Network,用顶点表示活动的网):用DAG图(有向无环图)表示一个工程。顶点表示活动,有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行。

2.拓扑排序:在图论中,由⼀个有向⽆环图的顶点组成的序列,当且仅当满⾜下列条件时,称为该图的⼀个拓扑排序:
- 每个顶点出现且只出现⼀次;
- 若顶点 A 在序列中排在顶点 B 的前⾯,则在图中不存在从顶点 B 到顶点 A 的路径。
- 或定义为:拓扑排序是对有向⽆环图的顶点的⼀种排序,它使得若存在⼀条从顶点 A 到顶点 B 的路径,则在排序中顶点 B 出现在顶点 A 的后⾯。每个 AOV ⽹都有⼀个或多个拓扑排序序列。
3.拓扑排序的实现:
- 从AoV网中选择一个没有前驱 (入度为0) 的顶点并输出
- 从网中删除该顶点和所有以它为起点的有向边。
- 重复D和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止
4.代码实现拓扑排序(邻接表实现):
#define MaxVertexNum 100 //图中顶点数目最大值typedef struct ArcNode{ //边表结点int adjvex; //该弧所指向的顶点位置struct ArcNode *nextarc; //指向下一条弧的指针
}ArcNode;typedef struct VNode{ //顶点表结点VertexType data; //顶点信息ArcNode *firstarc; //指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];typedef struct{AdjList vertices; //邻接表int vexnum,arcnum; //图的顶点数和弧数
}Graph; //Graph是以邻接表存储的图类型// 对图G进行拓扑排序
bool TopologicalSort(Graph G){InitStack(S); //初始化栈,存储入度为0的顶点for(int i=0;i<g.vexnum;i++){if(indegree[i]==0)Push(S,i); //将所有入度为0的顶点进栈}int count=0; //计数,记录当前已经输出的顶点数while(!IsEmpty(S)){ //栈不空,则存入Pop(S,i); //栈顶元素出栈print[count++]=i; //输出顶点ifor(p=G.vertices[i].firstarc;p;p=p=->nextarc){//将所有i指向的顶点的入度减1,并将入度为0的顶点压入栈v=p->adjvex;if(!(--indegree[v]))Push(S,v); //入度为0,则入栈}}if(count<G.vexnum)return false; //排序失败elsereturn true; //排序成功
}
五、关键路径
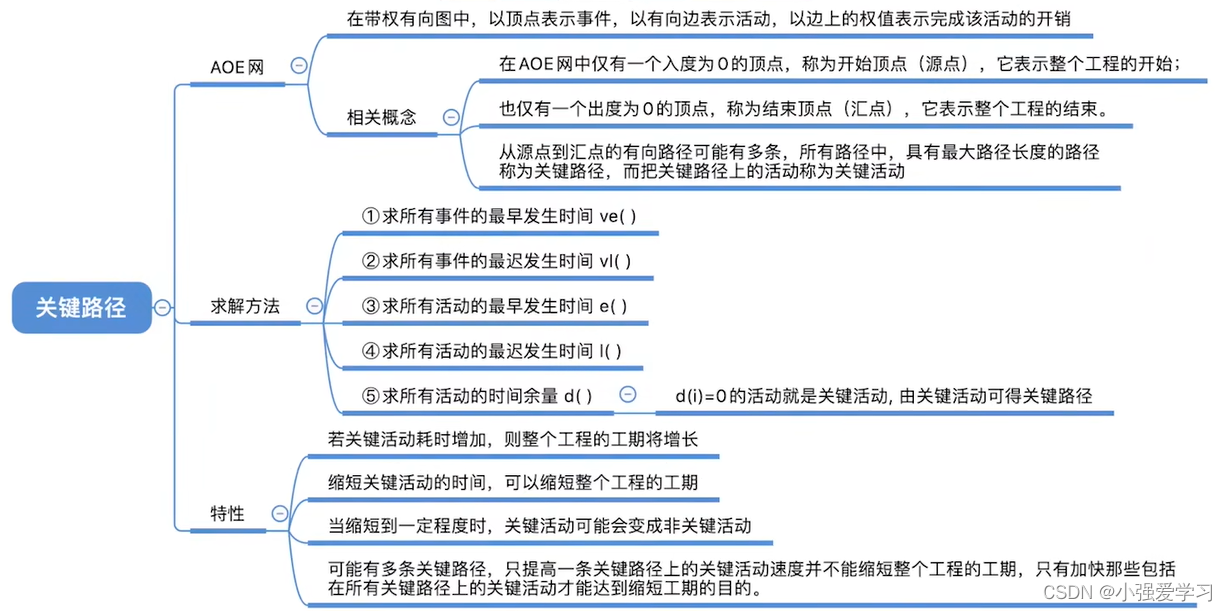
1.AOE 网:在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如 完成活动所需的时间),称之为⽤边表示活动的⽹络,简称 AOE ⽹ (Activity On Edge NetWork)。

2.AOE⽹具有以下两个性质:
- 只有在某顶点所代表的事件发⽣后,从该顶点出发的各有向边所代表的活动才能开始;
- 只有在进⼊某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发⽣。 另外,有些活动是可以并⾏进⾏的。
3.在 AOE ⽹中仅有⼀个⼊度为 0 的顶点,称为开始顶点(源点),它表示整个⼯程的开始; 也仅有⼀个出度为 0 的顶点,称为结束顶点(汇点),它表示整个⼯程的结束。
- 从源点到汇点的有向路径可能有多条,所有路径中,具有最⼤路径⻓度的路径称为关键路径,⽽把关键路径上的活动称为关键活动。
- 完成整个⼯程的最短时间就是关键路径的⻓度,若关键活动不能按时完成,则整个 ⼯程的完成时间就会延⻓。
相关文章:

【王道数据结构】第六章(下) | 图的应用
目录 一、最小生成树 二、最短路径 三、有向⽆环图描述表达式 四、拓扑排序 五、关键路径 一、最小生成树 1、最小生成树的概念 对于一个带权连通无向图G (V,E),生成树不,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所…...
)
Leetcode:518. 零钱兑换 II(C++)
目录 518. 零钱兑换 II 问题描述: 实现代码与解析: 动态规划(完全背包): 原理思路: 377. 组合总和 Ⅳ 问题描述: 实现代码与解析: 动态规划(完全背包࿰…...

Java中类是什么
类(class)是构造对象的模板或蓝图。 我们可以将类想象成制作小甜饼的模具,将对象想象为小甜饼。由类构造(construct)对象的过程称为创建类的实例(instance)。 正如前面所看到的,用Java 编写的所有代码都位于某个类里面。 标准 Java 库提供了几千个类&a…...
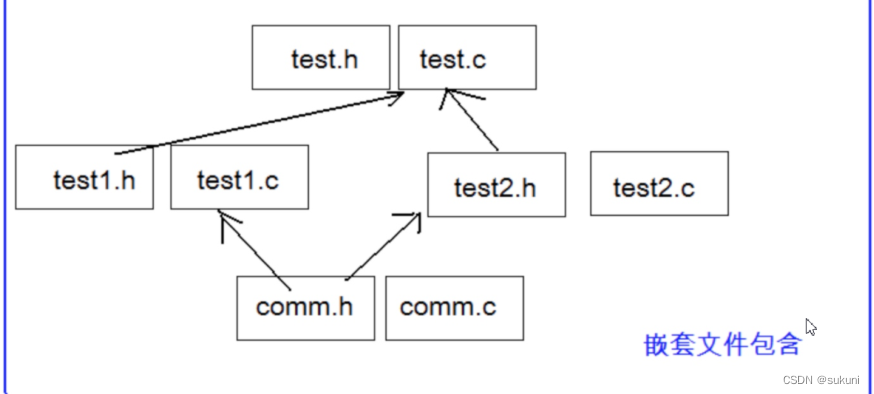
C进阶:预处理
🤖本篇文章主要讲解预处理的知识,即使你是小白也可以看的懂,若你对预处理有所不解,确定不来看看吗?😿 目录 一.代码运行是的两种环境 二.翻译环境 三.预定义符号 四.#define 1.define 定义宏 2.带有…...
侯捷C++系统工程师
前言我相信对于每一个学习C的同学和从业者来说,台湾著名学者侯捷老师的C系列都是不可错过的好视频。侯捷老师在网上已有五门课,分别是:C面向对象开发、STL标准库与泛型编程、C新标准C1&14、C内存管理机制以及C Startup揭秘讲师介绍侯捷老…...
ReentrantReadWriteLock、StampedLock
ReentrantLock、ReentrantReadWriteLock、StampedLock 读写锁 一个资源可以被多个读线程访问,或者被一个写线程访问,但是不能同时存在读写线程。 小口诀:读写互斥,读读共享 锁的演变 无锁-----> 独占锁----->读写锁---…...

Mysql中的事务、锁、日志详解
一、事务 1.事务特性及保证事务特性的原理 原子性:当前事务的操作要么全部成功,要么全部失败。原子性由undo log实现,undo log记录了每次操作之前的数据版本,如果某一操作失败,可以根据undo log回滚到最初状态。一致…...

k8s笔记24--安装metrics-server及错误处理
k8s笔记24--安装metrics-server及错误处理1 介绍2 安装3 常见错误第一次错误 持续 Failed probe第二次错误 bad status code "403 Forbidden"4 说明1 介绍 最近一个同事在老版本的 k8s 上安装metrics-server,pod一直处于running 非就绪状态,经…...
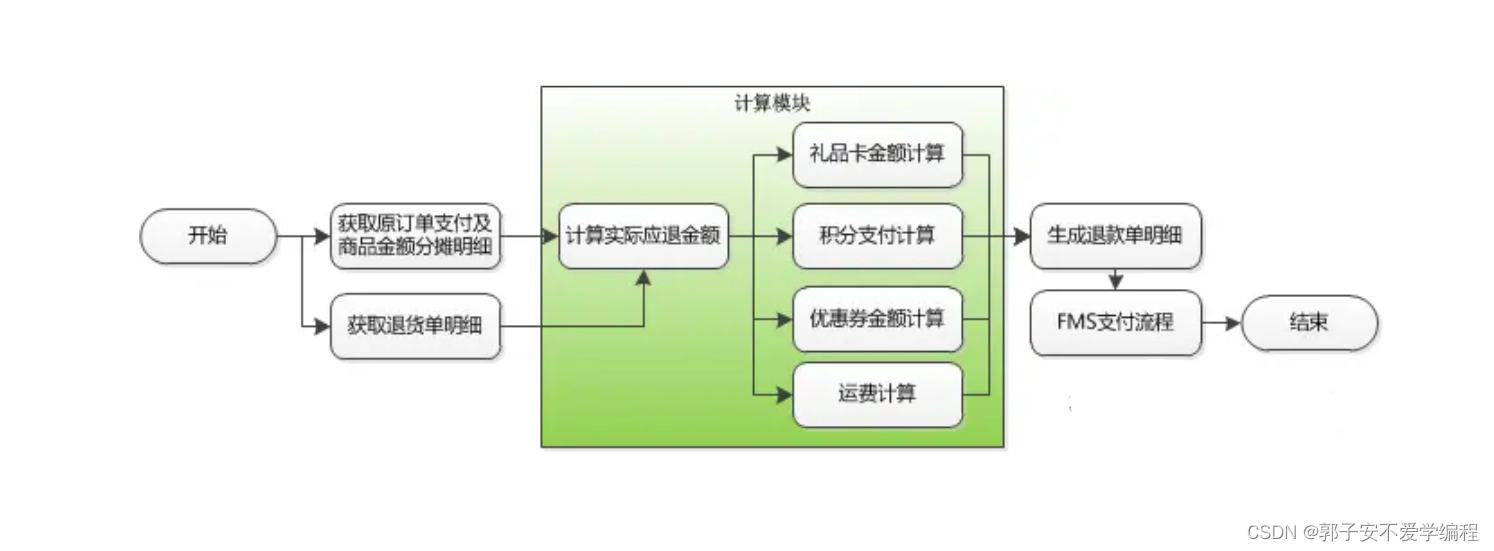
【电商】订单系统--售后的简易流程与系统关系
用户进行了订单签收并不意味着终结,这只是一个新的开始,因为商品送达后可能会由于运输过程包装或商品有破损,商品本质量并非商品详情中所描述的那样等各种原因使用户进行退货或换货;还有一种场景是用户签收后发现有的商品漏发、少…...

低代码开发平台|生产管理-成本核算搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建生产管理-成本核算。1.2、应用场景计算主生产及子生产计划的工序成本、领料成本,统计出总的生产成本金额。2、设置方法2.1、表单搭建1)新建表单【商品信息】,字段设置如下;名称…...

Xshell 安装及使用方法
公网地址:47.XXX.XXX.229 私网地址:172.XXX.128.XXX 用户:root 密码:1234561,百度xshell,下载,安装Xshell 2,填写配置及使用方式 主机:47.XXX.XXX.229 用户:root 密码&a…...

【Axure教程】转盘抽奖原型模板
转盘抽奖是营销活动中很常用的一种方式,在线上我们也可以经常看到转盘抽奖的活动,所以今天作者就教大家在Axure中怎么制作一个转盘抽奖的原型模板。一、效果展示1、可以随机转动轮盘,轮盘停止时,指针对着的奖品高亮显示2、可以重复…...

量子比特大突破!原子薄材料成为“救世主”
(图片来源:网络)量子计算是一项极其复杂的技术,现阶段的一些挑战正严重阻碍着它的发展,尤其是量子比特的小型化和质量问题。IBM计划在2023年实现具有1121个超导量子比特的处理器。以目前的技术手段,要达到这…...
Swagger3 API接口文档规范课程(内含教学视频+源代码)
Swagger3 API接口文档规范课程(内含教学视频源代码) 教学视频源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87431932 目录Swagger3 API接口文档规范课程(内含教学视频源代码)教学视频源代…...

数据库的基本操作
查看数据库语法格式:SHOW {DATABASES | SCHEMAS}[LIKE pattern | WHERE expr]#查看全部数据库mysql> show databases; -------------------- | Database | -------------------- | information_schema | | mysql | | performance_schema …...
分享5个超好用的Vue.js库
开发人员最好的朋友和救星就是这些第三方库,无论是开发新手还是经验丰富的老手,我们都喜欢开源软件包。借助开源库加速Vue项目的开发进度是现代前端开发比较常见的方式,这几个 Vue.js库,建议尽早用上,加速你的项目开发…...

第四章.误差反向传播法—ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现
第四章.误差反向传播法 4.2 ReLU/Sigmoid/Affine/Softmax-with-Loss层的实现 1.ReLU层 1).公式 2).导数: 3).计算图: 4).实现: class ReLU:def __init__(self):self.mask None# 正向传播def forward(self, x):self.mask (x < 0) # 输入…...
Python-第二天 Python基础语法
Python-第二天 Python基础语法一、 字面量1.1 常用的值类型1.1.1 字符串(string)二、注释2.1 注释的作用2.2 注释的分类三、变量3.1 什么是变量3.2 变量的特征四、数据类型4.1 数据类型4.2 type()语句4.3 type()语句的使用方式4.4 变量有类型吗ÿ…...
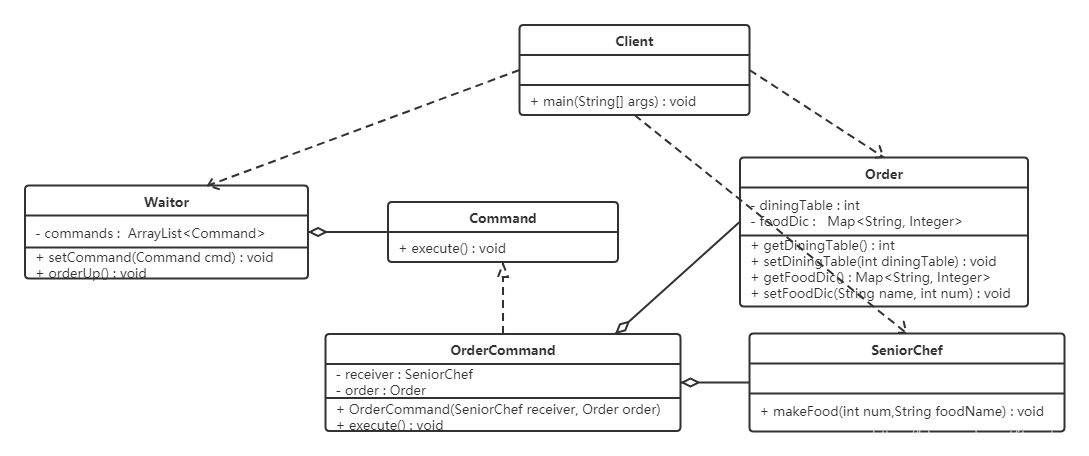
命令模式包含哪些主要角色?怎样实现命令?
命令模式包含以下主要角色:抽象命令类(Command)角色: 定义命令的接口,声明执行的方法。具体命令(Concrete Command)角色:具体的命令,实现命令接口;通常会持有…...

SpringCloud-Feign
Spring Cloud中集成Feign (只是笔记而已 其中有点命名啥的不对应,搜到了就划走吧) Feign--[feɪn]:Web 服务客户端,能够简化 HTTP 接口的调用。 没有Feign的之前服务提供者 package com.springcloudprovide.controller;import com.springclo…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
