机器学习:朴素贝叶斯分类器
贝叶斯决策论是概率框架下实施决策的基本方法,对分类任务来说,在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
贝叶斯定理是贝叶斯决策论的基础,描述了如何根据新的证据更新先验概率,贝叶斯定理:
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac {P(B|A) P(A)} {P(B)} P(A∣B)=P(B)P(B∣A)P(A)
| 后验概率 | P(A|B) | 在观测B的条件下A的概率 | 指在观测到数据之后,对某个假设的概率估计。它是通过贝叶斯定理计算得到的,结合了先验概率和似然概率。(事情已经发生,求这件事情发生的原因是由某个因素引起的可能性的大小。) |
| 似然概率 | P(B|A) | 在A发生的条件下B的概率 | 指在某个假设下,观测数据的概率。它描述了在某个假设下,数据出现的可能性。 |
| 先验概率 | P(A) | 没有观测到B的条件下A的概率 | 指在没有观测到任何数据之前,对某个事件的概率估计。它通常基于先验知识或经验。(根据以往经验或经过数据统计得到的概率。) |
| 边际概率 | P(B) | B的总概率 |
贝叶斯决策论通过结合先验知识和观测数据,使用贝叶斯定理计算后验概率,从而做出最优决策。即:
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) P(c|x) = \frac {P(c) P(x|c)} {P(x)} P(c∣x)=P(x)P(c)P(x∣c)
P©是样本空间中各类样本所占的比例,根据大数定理,当训练集包含充足的独立同分布样本时,P©可以通过各类样本所占的比例来进行估计。
但是对于类条件概率P(x|c)来说,涉及了关于x所有属性的联合概率,因此很难进行估计。
例如:每个样本具有d个属性,每个属性都有10个属性值,那么样本空间将有 1 0 d 10^d 10d种可能值,导致组合爆炸。
朴素贝叶斯对条件概率分布做了条件独立性假设
即,现在有 10 × d 10 \times d 10×d种可能值。
P ( x ∣ c ) = ∏ j = 1 n P ( x j ∣ c ) P(x|c) = \prod_{j=1}^{n}P(x^j|c) P(x∣c)=j=1∏nP(xj∣c)
先验概率:
P ( c k ) = ∑ i N I ( y i = c k ) N P(c_k) = \frac {\sum_i^NI(y_i = c_k)} {N} P(ck)=N∑iNI(yi=ck)
属性值是离散情况下,条件概率为:
P ( x j = a j l ∣ y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) P(x^j = a_{jl}|y = c_k) = \frac {\sum_{i=1}^NI(x_i^{(j)} = a_{jl}, y_i=c_k)} {\sum_{i=1}^{N}I(y_i=c_k)} P(xj=ajl∣y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck)
属性值是连续情况下,条件概率为:
假设概率密度P(x|c)服从正太分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2),通过极大似然估计得到的正态分布均值就是样本均值,方差就是 ( x − μ c ^ ) ( x − μ c ^ ) T (x - \hat{\mu_c})(x - \hat{\mu_c})^T (x−μc^)(x−μc^)T。
这样假设使其问题变得简单,但是估计准确性严重依赖所假设的概率分布形式是否符合潜在的真实数据分布。不过准确性却较高。
例如:

代码示例:
数据处理:将DataFrame转为numpy.array类型,并自定义分出训练集和测试集用来检验正确性。
import pandas as pd
import numpy as np
from io import StringIOdata = '编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜\n\
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是\n\
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是\n\
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是\n\
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是\n\
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是\n\
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是\n\
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是\n\
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是\n\
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否\n\
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否\n\
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否\n\
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否\n\
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否\n\
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否\n\
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否\n\
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否\n\
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否'df = pd.read_csv(StringIO(data))
# print(df.info())def obj_to_int(series: pd.Series):return pd.Categorical(series).codesdef label_encoder(df: pd.DataFrame):for col in df.columns:if df[col].dtype == 'object':df[col] = obj_to_int(df[col])return df# 已完成:2025年2月9日 14点27分
# # 保存处理后的数据
# df = label_encoder(df)
# df.to_csv('data.csv', index=False)# # 已完成:2025年2月9日 14点30分
# # 随机选择三行作为测试集
# test_set = df.sample(n=3, random_state=42)
# # 获取剩余的行作为训练集
# train_set = df.drop(test_set.index)
# # 保存训练集和测试集
# train_set.to_csv('train.csv', index=False)
# test_set.to_csv('test.csv', index=False)def get_train_data():df = pd.read_csv('train.csv')return np.array(df.iloc[:, :])def get_test_data():# 2025年2月9日 16点19分df = pd.read_csv('test.csv')return np.array(df.iloc[0:, :])# 随机选择一半的数据作为训练集# df = pd.read_csv('data.csv')# bool_array = np.random.choice([True, False], size=len(df), p=[0.5, 0.5])# return np.array(df[bool_array].iloc[:, :])
# print(get_train_data())
# print(get_test_data())
朴素贝叶斯:
-
计算先验概率
def get_prior_prob(train_data: np.array):# 先验概率prior_prob = {}# 计算先验概率for i in range(len(train_data)):if train_data[i][-1] not in prior_prob:prior_prob[int(train_data[i][-1])] = 1else:prior_prob[int(train_data[i][-1])] += 1for key in prior_prob:prior_prob[key] /= len(train_data)return prior_prob -
计算条件概率
-
离散值
n = len(train_data[0]) - 1cond_prob = [ {} for i in range(n) ]# 计算条件概率# (特征值, 类别) -> 出现次数fea_res_cnt = [[0,0] for i in range(n)]for i in range(len(train_data)):for j in range(1, n):if int(train_data[i][-1]) == 0:fea_res_cnt[j][0] += 1else: fea_res_cnt[j][1] += 1for i in range(len(train_data)):# 仅计算特征值为离散值的条件概率for j in range(1, n - 2):fea = int(train_data[i][j])res = int(train_data[i][-1])if (fea, res) not in cond_prob[j]:cond_prob[j][(fea, res)] = 1else:cond_prob[j][(fea, res)] += 1 -
连续值:使用极大似然法球的均值、标准差,进行正太分布
# 计算特征值为连续值的条件概率reslist = [ [ [] for i in range(2)] for j in range(2)]for i in range(len(train_data)):for j in range(n - 2, n):res = int(train_data[i][-1])reslist[j - n + 2][res].append(float(train_data[i][j]))for i in range(2):for j in range(2):mean,std = np.mean(reslist[i][j]),np.std(reslist[i][j])cond_prob[i + n - 2][(j, mean, std)] = 0
总的这个函数代码:
def get_cond_prob(train_data: np.array):n = len(train_data[0]) - 1cond_prob = [ {} for i in range(n) ]# 计算条件概率# (特征值, 类别) -> 出现次数fea_res_cnt = [[0,0] for i in range(n)]for i in range(len(train_data)):for j in range(1, n):if int(train_data[i][-1]) == 0:fea_res_cnt[j][0] += 1else: fea_res_cnt[j][1] += 1for i in range(len(train_data)):# 仅计算特征值为离散值的条件概率for j in range(1, n - 2):fea = int(train_data[i][j])res = int(train_data[i][-1])if (fea, res) not in cond_prob[j]:cond_prob[j][(fea, res)] = 1else:cond_prob[j][(fea, res)] += 1# 计算特征值为连续值的条件概率reslist = [ [ [] for i in range(2)] for j in range(2)]for i in range(len(train_data)):for j in range(n - 2, n):res = int(train_data[i][-1])reslist[j - n + 2][res].append(float(train_data[i][j]))for i in range(2):for j in range(2):mean,std = np.mean(reslist[i][j]),np.std(reslist[i][j])cond_prob[i + n - 2][(j, mean, std)] = 0# 计算条件概率for i in range(1, n - 2):for key in cond_prob[i]:cond_prob[i][key] /= fea_res_cnt[i][key[1]]return cond_prob -

-
进行测试
# 正太分布密度概率 def probability_density_function(mean:float, std:float, var:float) -> float:return (1/(std * np.sqrt(2 * np.pi))) * np.
exp(-0.5 * ((var - mean)/std)**2)def test():cond_prob = get_cond_prob(get_train_data())prior_prob = get_prior_prob(get_train_data())test_data = get_test_data()# 预测right_cnt = 0for i in range(len(test_data)):good = bad = 1good = prior_prob[1]bad = prior_prob[0]for j in range(len(cond_prob)):for key in cond_prob[j]:if len(key) == 2:if key[1] == 0:bad *= cond_prob[j][(int(test_data[i][j]), key[1])]else:good *= cond_prob[j].get((int(test_data[i][j]), key[1]), 0) # 有可能出现未知的特征值elif len(key) == 3:if key[0] == 0:bad *= probability_density_function(key[1], key[2], float(test_data[i][j]))else:good *= probability_density_function(key[1], key[2], float(test_data[i][j]))if good > bad:print('good')if int(test_data[i][-1]) == 1:print('right')right_cnt += 1else:print('bad')if int(test_data[i][-1]) == 0:print('right')right_cnt += 1print(f'accuracy: {right_cnt / len(test_data)}')
朴素贝叶斯(Naive Bayes)算法理论与实践 - 简书 (jianshu.com)
相关文章:

机器学习:朴素贝叶斯分类器
贝叶斯决策论是概率框架下实施决策的基本方法,对分类任务来说,在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。 贝叶斯定理是贝叶斯决策论的基础,描述了如何根据新的证据更新先验概率,贝叶斯定理&…...

打开Visual Studio Code的时候发现未检测到适用于linux的windows子系统,那么该问题要如何解决?
两个月没有使用vscode编写代码,今天使用的时候发现了以上的问题导致我的vscode无法编写程序,接下来我将本人解决该问题的思路分享给大家。 首先我们要清楚WSL是适用于linux的window的子系统,是一个在Windows 10\11上能够运行原生Linux二进制可…...

力扣24题——两两交换链表中节点
#题目 #代码 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val val; }* ListNode(int val, ListNode next) { this.val val; this.next next; }* }*/ clas…...

android launcher拖动图标释放错位
由于为了设备流畅把所有动画效果设置为0.5,不设置为0是因为锁屏在开机时会有闪黑屏的现象。在此背景下,测试发现在拖动桌面图标时,在图标动画过程中错位时释放图标,则图标会留在错位的位置,不会自动对齐。 原因就是动…...

window ssh免密码输入
生成本地公钥 打开dos,使用以下命令手动生成一个公钥: ssh-keygen -t rsa Generating public/private rsa key pair. Enter file in which to save the key (C:\Users\aero/.ssh/id_rsa): Enter passphrase (empty for no passphrase): Enter same pas…...

2024年博客之星年度评选—主题文章创作评审文章得分公布
博客之星活动地址:https://www.csdn.net/blogstar2024 创作影响力评审入围名单:https://blogdev.blog.csdn.net/article/details/145189549 目录 主题文章创作评审得分排名 主题文章创作说明 主题文章评选说明 创作影响力评审主题文章创作评审目前排名 博…...

vscode插件Remote - SSH使用教程
Remote - SSH 是一款非常实用的 Visual Studio Code (VSCode) 扩展插件,它允许开发者通过SSH连接到远程服务器,并像在本地一样进行代码编辑和调试。这意味着你可以直接在VS Code中打开位于远程机器上的文件夹,并利用本地安装的VS Code功能,如语法高亮、智能感知、Git集成等…...

自学人工智能大模型,满足7B模型的训练和微调以及推理,预算3万,如何选购电脑
如果你的预算是 3万元人民币,希望训练和微调 7B 参数规模的人工智能大模型(如 LLaMA、Mistral 等),你需要一台高性能的深度学习工作站。在这个预算范围内,以下是推荐的配置: 1. 关键硬件配置 (1) GPU (显卡…...

github不翻墙就可以访问
目录 简介资料准备windows平台设置下载运行git设置firefox设置 ubuntu平台设置下载启动服务设置系统代理git设置firefox设置证书 注意事项 简介 由于github访问不稳定,严重影响了国内软件开发,在网上搜索并验证了一些方法.现在整理出来一个可以正常使用的方法, 在windows和Lin…...
)
十大知识领域中涉及到的工具与技术(三)
简介 整理下十大知识领域中使用到 “ 数据表现 ” 里面所包含的工具与技术,以及在那些过程中有使用。 具体的一些工具与技术 工具与技术—————————————描述1.亲和图用于对大量创意进行分组的技术。与心智图相似。针对某个问题,产生出可联成…...
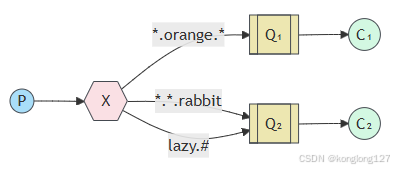
在nodejs中使用RabbitMQ(三)Routing、Topics、Headers
示例一、Routing exchange类型direct,根据消息的routekey将消息直接转发到指定队列。producer.ts 生产者主要发送消息,consumer.ts负责接收消息,同时也都可以创建exchange交换机,创建队列,为队列绑定exchangeÿ…...

设计模式全解(含代码实例)
目录 设计模式概念耦合与解耦 常见-5种全部-23种创建型模式(Creational Patterns)单例模式(Singleton Pattern)工厂方法模式(Factory Method Pattern):抽象工厂模式(Abstract Factor…...

springboot019-爬虫基于网页开发和数据抓取技术的在线新闻聚合平台的设计与实现
💕💕作者: 小九学姐 💕💕个人简介:十年Java,Python美女程序员一枚,精通计算机专业前后端各类框架。 💕💕各类成品Java毕设 。javaweb,ssm…...

#渗透测试#批量漏洞挖掘#LiveBos UploadFile 任意文件上传漏洞
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停止本文章读。 目录 漏洞背景 漏洞成因 影响评估 检测方案 …...

【分布式架构理论3】分布式调用(1):负载均衡
文章目录 零、三种不同的负载均衡一、常见行业负载均衡方案1. 电商与互联网服务2. 金融与支付系统3. 云计算与分布式存储 二、负载均衡策略概述1. 无状态负载均衡(强调公平性)2. 有状态的负载均衡(强调正确性) 三、 总结 零、三种…...

如何安装和运行Zonos:详细步骤指南
如何安装和运行Zonos:详细步骤指南 1. 安装依赖2. 克隆 Zonos 仓库3. 创建 Python 虚拟环境4. 安装 Zonos5. 运行 Zonos6. 总结 Zonos 是一个基于 Python 的语音合成工具,它结合了先进的深度学习技术和语音生成模型,能够生成高质量的语音输出…...

docker学习---第3步:docker实操大模型
文章目录 1.Images2.Container3.DockerfileENTRYPOINT和CMDCOPY和ADDLABLE、EXPOSE和VOLUME卷中的数据是如何做数据备份的? ARG和ENVHEALTHCHECK 跟着b站 胖虎遛二狗学习 Docker动手入门 | 大模型工程师必备技能 (🎉已完结&…...

记录第一次在windows环境编译libuvc库 踩的坑
最近遇到windows下编译libuvc库,实现经usb连接的摄像头拍摄采集。绕了一大圈,记录一下。 首先,作为新手,肯定需要参考大神资料,但是还是踩了坑。 要在windows 环境下安装libuvc的驱动并确保可用,需要经过一系列流程&a…...

快速集成DeepSeek到项目
DeepSeek API-KEY 获取 登录DeekSeek 官网,进入API 开放平台 2. 创建API-KEY 复制API-KEY进行保存,后期API调用使用 项目中集成DeepSeek 这里只展示部分核心代码,具体请查看源码orange-ai-deepseek-biz-starter Slf4j AllArgsConstructo…...

基础连接已经关闭: 服务器关闭了本应保持活动状态的连接
您在进行 HTTP 请求时遇到“基础连接已经关闭: 服务器关闭了本应保持活动状态的连接”的错误,这通常与连接的保持活动(Keep-Alive)设置有关。以下是可能的原因和解决方法: 可能的原因: Keep-Alive 设置: 默…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
