机器学习·逻辑回归
前言
逻辑回归虽然名称中有 “回归”,但实际上用于分类问题。基于线性回归的模型,通过使用逻辑函数(如 Sigmoid 函数)将线性组合的结果映射到0到1之间的概率值,用于表示属于某个类别的可能性。
一、逻辑回归 vs 线性回归
| 特性 | 逻辑回归 | 线性回归 |
|---|---|---|
| 任务类型 | 分类(二分类为主) | 回归(预测连续值) |
| 输出范围 | (0,1)(概率值) | (-∞, +∞) |
| 核心函数 | Sigmoid 函数 | 线性函数 |
| 损失函数 | 对数损失函数(交叉熵) | 均方误差(MSE) |
| 优化目标 | 最大化似然函数 | 最小化预测误差平方和 |
二、核心数学原理
1. Sigmoid 函数
-
公式:
\( \sigma(z) = \frac{1}{1 + e^{-z}} \) -
作用:将线性组合 \( z = w^T x \) 映射到 (0,1) 区间,表示概率。
-
特性:
-
输出值可解释为样本属于正类的概率:\( P(y=1|x) = \sigma(w^T x) \)
-
当 \( z = 0 \) 时,\( \sigma(z) = 0.5 \),为分类决策边界。
-
2. 损失函数(对数损失)
-
公式:
\( J(w) = -\frac{1}{m} \sum_{i=1}^m [y^{(i)} \log(h_w(x^{(i)})) + (1-y^{(i)}) \log(1 - h_w(x^{(i)}))] \) -
特点:
-
凸函数,可通过梯度下降求全局最优解。
-
惩罚预测概率与真实标签的偏离程度。
-
3. 梯度下降
-
权重更新公式:
\( w \leftarrow w - \alpha \cdot \frac{1}{m} X^T (h_w(X) - y) \) -
关键参数:
-
学习率 \( \alpha \):控制步长,需调参避免震荡或收敛过慢。
-
迭代次数:通常结合早停法(如
tol参数)确定终止条件。
-
三、逻辑回归的 Python 实现
1. 手动实现核心代码
import numpy as npdef sigmoid(z):return 1 / (1 + np.exp(-z))def logistic_regression(X, y, lr=0.01, num_iter=10000):m, n = X.shapeX = np.concatenate((np.ones((m, 1)), X), axis=1) # 添加截距项w = np.zeros(n + 1)for _ in range(num_iter):z = np.dot(X, w)h = sigmoid(z)gradient = np.dot(X.T, (h - y)) / mw -= lr * gradientreturn w2. 决策边界可视化
import matplotlib.pyplot as plt# 假设 w 为训练得到的权重 [w0, w1, w2]
x1 = np.linspace(X[:,0].min(), X[:,0].max(), 100)
x2 = -(w[0] + w[1] * x1) / w[2] # 解方程 w0 + w1x1 + w2x2 = 0plt.scatter(X[:,0], X[:,1], c=y)
plt.plot(x1, x2, 'r-')
plt.show()四、Scikit-learn 实现
from sklearn.linear_model import LogisticRegression# 创建模型(带 L2 正则化)
model = LogisticRegression(penalty='l2', C=1.0, max_iter=1000)
model.fit(X_train, y_train)# 评估模型
print("准确率:", model.score(X_test, y_test))
print("权重:", model.coef_)
print("截距:", model.intercept_)五、一些问题
1. 为什么逻辑回归叫“回归”?
-
历史原因:虽然用于分类,但其数学形式继承自线性回归(通过线性组合 \( w^T x \) 建模)。
-
本质区别:通过 Sigmoid 函数将线性输出映射为概率,解决分类问题。
2. 为什么使用对数损失而非均方误差?
-
数学原因:均方误差在逻辑回归中会导致非凸优化问题,难以找到全局最优解。
-
概率解释:对数损失直接衡量预测概率分布与真实分布的差异。
3. 逻辑回归的局限性
-
线性决策边界:无法直接处理非线性可分数据(可通过引入多项式特征解决)。
-
多分类扩展:需借助 One-vs-Rest 或 Softmax 回归(多分类逻辑回归)。
六、应用
-
二分类问题:如垃圾邮件检测、疾病诊断。
-
概率预测:如用户点击广告的概率、信用卡违约概率。
-
特征重要性分析:通过权重系数大小判断特征对结果的影响方向及程度。
七、完整代码+示例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report# ======================
# 1. 生成模拟数据集
# ======================
X, y = make_classification(n_samples=500, # 样本数量n_features=2, # 特征数量n_redundant=0, # 无冗余特征n_clusters_per_class=1, # 每类样本聚集程度random_state=42
)
X = (X - X.mean(axis=0)) / X.std(axis=0) # 标准化数据(提升梯度下降效率)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# ======================
# 2. 手动实现逻辑回归
# ======================
class LogisticRegressionManual:def __init__(self, learning_rate=0.01, n_iters=1000):self.lr = learning_rateself.n_iters = n_itersself.weights = Noneself.bias = Noneself.loss_history = []def _sigmoid(self, z):return 1 / (1 + np.exp(-z))def fit(self, X, y):n_samples, n_features = X.shapeself.weights = np.zeros(n_features)self.bias = 0# 梯度下降优化for _ in range(self.n_iters):linear_model = np.dot(X, self.weights) + self.biasy_pred = self._sigmoid(linear_model)# 计算梯度dw = (1 / n_samples) * np.dot(X.T, (y_pred - y))db = (1 / n_samples) * np.sum(y_pred - y)# 更新参数self.weights -= self.lr * dwself.bias -= self.lr * db# 记录损失loss = -np.mean(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred))self.loss_history.append(loss)def predict_proba(self, X):linear_model = np.dot(X, self.weights) + self.biasreturn self._sigmoid(linear_model)def predict(self, X, threshold=0.5):return (self.predict_proba(X) >= threshold).astype(int)# 训练手动实现的模型
manual_model = LogisticRegressionManual(learning_rate=0.1, n_iters=2000)
manual_model.fit(X_train, y_train)# ======================
# 3. Scikit-learn实现
# ======================
sklearn_model = LogisticRegression(penalty='none', solver='lbfgs', max_iter=2000)
sklearn_model.fit(X_train, y_train)# ======================
# 4. 结果可视化
# ======================
def plot_decision_boundary(model, X, y, title):x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),np.linspace(y_min, y_max, 100))# 预测网格点Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap='coolwarm')plt.title(title)plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plot_decision_boundary(manual_model, X_train, y_train, 'Manual Logistic Regression')plt.subplot(1, 2, 2)
plot_decision_boundary(sklearn_model, X_train, y_train, 'Scikit-learn Logistic Regression')plt.tight_layout()
plt.show()# ======================
# 5. 模型评估
# ======================
# 手动模型评估
y_pred_manual = manual_model.predict(X_test)
print("手动实现模型评估:")
print(f"准确率: {accuracy_score(y_test, y_pred_manual):.4f}")
print(classification_report(y_test, y_pred_manual))# Scikit-learn模型评估
y_pred_sklearn = sklearn_model.predict(X_test)
print("\nScikit-learn模型评估:")
print(f"准确率: {accuracy_score(y_test, y_pred_sklearn):.4f}")
print(classification_report(y_test, y_pred_sklearn))# ======================
# 6. 损失函数变化曲线
# ======================
plt.figure(figsize=(8, 5))
plt.plot(manual_model.loss_history, label='Training Loss')
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Loss During Training (Manual Implementation)')
plt.legend()
plt.show()-
Sigmoid函数:将线性输出映射到(0,1)区间,表示概率。
-
对数损失函数:衡量预测概率与真实标签的差异。
-
梯度下降:通过计算损失函数的梯度更新模型参数。
-
决策边界:由权重和偏置定义的超平面,将不同类别分开。
相关文章:

机器学习·逻辑回归
前言 逻辑回归虽然名称中有 “回归”,但实际上用于分类问题。基于线性回归的模型,通过使用逻辑函数(如 Sigmoid 函数)将线性组合的结果映射到0到1之间的概率值,用于表示属于某个类别的可能性。 一、逻辑回归 vs 线性回…...

C#上位机--结构
引言 在 C# 上位机开发中,我们常常需要处理各种数据,例如从硬件设备采集到的传感器数据、与下位机通信时传输的数据包等。结构(struct)作为 C# 中的一种值类型,在这种场景下有着广泛且重要的应用。它可以将多个相关的…...

hydra.utils.instantiate函数介绍
hydra.utils.instantiate 是 Hydra 提供的一个动态实例化函数,它可以根据 OmegaConf 配置字典(DictConfig) 自动创建 Python 对象(如类、函数等)。 它的主要作用是: ✅ 从配置文件动态创建对象(…...

Qt的QTableWidget样式设置
在 Qt 中,可以通过样式表(QSS)为 QTableWidget 设置各种样式。以下是一些常见的样式设置示例: 1. 基本样式设置 tableWidget->setStyleSheet(// 表格整体样式"QTableWidget {"" background-color: #F0F0F0;…...
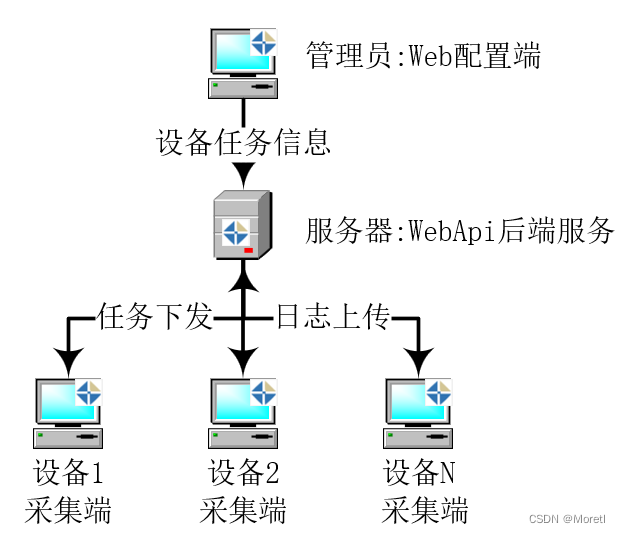
Moretl 增量文件采集工具
永久免费: <下载> <使用说明> 用途 定时全量或增量采集工控机,电脑文件或日志. 优势 开箱即用: 解压直接运行.不需额外下载.管理设备: 后台统一管理客户端.无人值守: 客户端自启动,自更新.稳定安全: 架构简单,兼容性好,通过授权控制访问. 架构 技术架构: Asp…...
(CVE-2024-57241))
dedecms 开放重定向漏洞(附脚本)(CVE-2024-57241)
免责申明: 本文所描述的漏洞及其复现步骤仅供网络安全研究与教育目的使用。任何人不得将本文提供的信息用于非法目的或未经授权的系统测试。作者不对任何由于使用本文信息而导致的直接或间接损害承担责任。如涉及侵权,请及时与我们联系,我们将尽快处理并删除相关内容。 0x0…...

深入理解 MyBatis 框架的核心对象:SqlSession
Mybatis框架中的SqlSession对象详解 引言 MyBatis 是一个优秀的持久层框架,它支持定制化 SQL、存储过程以及高级映射。MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集的工作。MyBatis 可以使用简单的 XML 或注解来配置和映射原生信息࿰…...
)
ndk 编译opencv(去除libandroid.so mediandk依赖)
简单的bash运行 需要关注的: OPENCV_EXTRA_MODULES_PATH : opencv contrib库BUILD_opencv_XXX :添加contrib库后默认是contrib库全部编译,用这个控制需要关闭的NDK的路径 export ANDROID_NDK/media/hello/data/3rd_party/25.2.…...

MySQL索引和其底层数据结构介绍
索引在项目中非常常见,它是一种帮助MySQL高效获取数据的数据结构,主要用来提高数据检索效率,降低数据库的I/O成本。同时,索引列可以对数据进行排序,降低数据排序的成本,也能减少CPU的消耗。就像是书的目录&…...

No module named ‘posepile.util‘
目录 No module named posepile.util 解决方法: No module named posepile.util 错误代码: import posepile.datasets3d as ds3d pip install git+https://github.com/isarandi/PosePile.git. And then, I executed the following command, " python -m metrabs_py…...

SQL布尔盲注、时间盲注
一、布尔盲注 布尔盲注(Boolean-based Blind SQL Injection)是一种SQL注入技术,用于在应用程序不直接显示数据库查询结果的情况下,通过构造特定的SQL查询并根据页面返回的不同结果来推测数据库中的信息。这种方法依赖于SQL查询的…...

RocketMQ与kafka如何解决消息丢失问题?
0 前言 消息丢失基本是分布式MQ中需要解决问题,消息丢失时保证数据可靠性的范畴。如何保证消息不丢失程序员面试中几乎不可避免的问题。本文主要说明RocketMQ和Kafka在解决消息丢失问题时,在生产者、Broker和消费者之间如何解决消息丢失问题。 1.Rocket…...

Uniapp 获取定位详解:从申请Key到实现定位功能
文章目录 前言一、申请定位所需的 Key1.1 注册高德开发者账号1.2 创建应用1.3 添加 Key 二、在 Uniapp 中配置定位功能2.1 引入高德地图 SDK2.2 获取定位权限 三、实现定位功能3.1 使用 uni.getLocation 获取位置3.2 处理定位失败的情况3.3 持续定位3.4 停止持续定位 四、总结 …...

【Vue3 入门到实战】14. telePort 和 Suspense组件
目录 编辑 1. telePort 2. 异步组件Suspense 3. 总结 1. telePort telePort 允许你将子组件渲染到 DOM 中的任何位置,而不仅仅是在其父组件的范围内。这对于模态框(modals)、提示框(tooltips)和其他需要脱…...

Golang的并发编程案例详解
Golang的并发编程案例详解 一、并发编程概述 并发编程是指程序中有多个独立的执行线索,并且这些线索在时间上是重叠的。在 Golang 中,并发是其核心特性之一,通过 goroutine 和 channel 来支持并发编程,使得程序可以更高效地利用计…...

IS-IS 泛洪机制 | LSP 处理流程
IS-IS 泛洪机制 作为一种链路状态路由协议,IS-IS 与 OSPF 类似,在学习和计算路由之前,区域中的路由器首先需交换链路状态信息,最终使所有路由器的链路状态数据库达到一致状态,这就如同每台路由器都拥有一张相同的网络…...
)
原型模式详解(Java)
原型模式(Prototype Pattern),作为一种极具代表性的创建型设计模式,其核心思想在于通过复制,亦即克隆现有的对象,来达成创建新对象的目的,而非依赖传统的构造函数途径。这一模式巧妙地基于现有对…...

内存条2R×4 2400和4R×4 2133的性能差异
内存条2R4 2400和4R4 2133的性能差异 2R4 2400 和 4R4 2133 是两种不同的内存条规格,主要在Rank数量和频率上有所不同,具体性能差异如下: 1. Rank数量 2R4:表示内存条有2个Rank,每个Rank有4个内存芯片。4R4ÿ…...

安装并配置 MySQL
MySQL 是世界上最流行的开源关系型数据库管理系统之一,因其高性能、可靠性和易用性而被广泛应用于各种规模的企业级应用中。本文将详细介绍如何在不同的操作系统上安装和配置 MySQL,帮助你快速搭建起一个功能完善的数据库环境。 选择适合你的安装方式 …...

常用的网络安全设备
一、 WAF 应用防火墙 范围:应用层防护软件 作用: 通过特征提取和分块检索技术进行模式匹配来达到过滤,分析,校验网络请求包的目的,在保证正常网络应用功能的同时,隔绝或者阻断无效或者非法的攻击请求 可…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
