傅里叶变换推导
基本模型
假设在二维直角坐标系中,可以用相互垂直的基向量
和
表示:

假设:
假设在
上的投影为
,那么:
所以:
用公式表达:
但是在实际中,基向量和
不一定长度都是1,重新推导一下:
假设:
那么:
两边乘以:
分子部分其实就是求在
上的投影与
的乘积,所以:
带入数据:
大功告成。
结论:
从二维到无限维
二维模型如下:
| 向量 | 维度1的投影 | 维度2的投影 |
| 2 | 3 | |
| 1 | 0 | |
| 0 | 1 |
扩展到三维:
| 向量 | 维度1的投影 | 维度2的投影 | 维度3的投影 |
| c1 | c2 | c3 | |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 0 | 1 |
可以看到,有多少个维度就要有多少个基向量,每个基向量的维度和
相等。
扩展到无限维:
| 向量 | 维度1的投影 | 维度2的投影 | 维度3的投影 | 维度n的投影 |
| c1 | c2 | c3 | cn | |
| 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 1 |
把函数当成无限维向量
把函数的t当成无限维,它的值分布在各自的维度上:
| 函数 | ||||
于是:
这里有个容易让人困惑的点:
前面的各个基向量都是这样的:
| 向量 | 维度1的投影 | 维度2的投影 | 维度3的投影 | 维度n的投影 |
| 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 1 |
每个向量只在自己的维度有值,在别的维度为0。
那现在的函数在别的维度上等于0吗?
不一定,但是没错。
首先各个维度的基向量是正交(垂直)的,比如:
这里的函数其实也是正交的:
两边乘以:
在傅里叶变换中:
各个基函数=
其中是步长的意思,任你选取,n=1,2,...
总的意思就是f(t)可以表示成很多正交的、不同频率(一个频率就是一个维度)的三角函数之和。
可以证明:
与
正交,
与
正交。
于是:
好了,已知了,
怎么求?
由前面的公式:
可以推导出:
套用之前两边乘以dt的方法:
带入,
:
这便是傅里叶级数了。
其它
各个基函数必须是两两正交的,不然所有推导都是错的。
好多资料说两个函数的正交等于它们的内积:
但是由向量的点积推出来应该是这样才对:
可这样也是不对的,不存在这种操作。在我的推导中用了这个等式,但是我分子分母约掉dt了,所以避开了。
相关文章:
傅里叶变换推导
基本模型 假设在二维直角坐标系中,可以用相互垂直的基向量和表示: 假设: 假设在上的投影为,那么: 所以: 用公式表达: 但是在实际中,基向量和不一定长度都是1,重新推导一…...

扣子工作流中禁止同类别的图像流节点,不能超过4个
一、问题1不能在一个工作流中超过4个图像的并行节点 1、现象 本来想着在扣子中一次生成多张图片。 然后问了扣子小助手 2、图像节点限制 扣子给了如下反馈 近期图像流上线了并发限额,具体规则如下: 针对对象:单用户维度,非 bot…...

Java 语言深度剖析与实践应用
一、引言 Java 作为一种广泛应用于各种领域的编程语言,自 1995 年诞生以来,凭借其跨平台性、面向对象特性、丰富的类库以及强大的生态系统,在软件开发行业占据着重要地位。无论是企业级应用开发、移动应用开发、大数据处理还是分布式系统构建…...

1.14学习总结
日常刷题单 刷了题目后,对于排序方法更加熟练,手搓代码的速度也得到了提高。 感觉字符串还不熟练,高精度更是云里雾里,上升空间极大。 同时看见今晚有个入门难度的测试,去练了练手,想看看自己是什么成分&…...

C++蓝桥杯基础篇(三)
片头 哈喽!小伙伴们,大家好~,今天我们来学习蓝桥杯基础篇(三),继续练习相关习题,准备好了吗?我们开始啦~ 一、while循环 可以简单理解为循环版的if语句。if语句是判断1次࿰…...

微信小程序的制作
制作微信小程序的过程大致可以分为几个步骤:从环境搭建、项目创建,到开发、调试和发布。下面我会为你简要介绍每个步骤。 1. 准备工作 在开始开发微信小程序之前,你需要确保你已经完成了以下几个步骤: 注册微信小程序账号&…...

Sass更新:@import——>@use
背景:将一个公共的CSS样式文件导入到任意一个组件中进行使用 一、创建并使用CSS公共样式文件 1、在目录的assets目录下创建一个style文件夹,里面存放一个.scss文件(例:mixin.scss) 2、文件内以mixin来设置名为flex的…...
Python使用Flask结合DeepSeek开发
一、背景 我之前关于DeepSeek使用ollama部署的文章大家可以把DeepSeek大模型部署起来。那么ollama还提供了可以调用对应部署模型的API接口。我们可以基于这些接口,做自己的二次开发。使用pythonflaskollama就可以进行模型对话调用。并且前端采用SSE的技术࿰…...

python中的抽象类在项目中的实际应用
抽象类在项目中的实际应用主要体现在 规范代码结构、强制子类实现某些方法、提供部分通用功能,让代码更稳定、易维护。 举个例子:数据校验器 假设你在做一个 用户输入校验系统,需要支持 数字校验、字符串校验 和 邮箱校验。如果不用抽象类&…...
)
New Game--(单调队列)
I - New Game 有一种新的游戏,Monocarp 想要玩。这个游戏使用一副包含 n 张牌的牌堆,其中第 i 张牌上写有一个整数 a_i。 在游戏开始时,Monocarp 可以在第一轮选择牌堆中的任意一张牌。在接下来的每一轮中,Monocarp 可以选择一张…...

mapbox V3 新特性,添加下雪效果
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:mapbox 从入门到精通 文章目录 一、🍀前言1.1 ☘️mapboxgl.Map 地图对象…...

无人机遥感在农林信息提取中的实现方法与GIS融合制图教程
遥感技术作为一种空间大数据手段,能够从多时、多维、多地等角度,获取大量的农情数据。数据具有面状、实时、非接触、无伤检测等显著优势,是智慧农业必须采用的重要技术之一。 一:综合态势分析 1.1 研究区及作物品种分析 ÿ…...
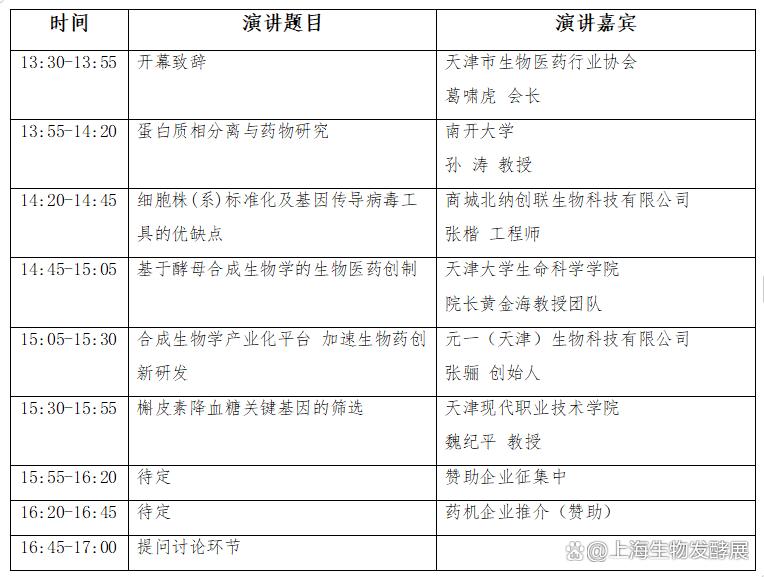
生物发酵展与2025生物医药创新技术与应用发展论坛同期盛大举办
近日,备受瞩目的生物发酵展与2025生物医药创新技术与应用发展论坛暨展览会宣布将同期盛大举办。这一消息标志着生物科技领域两大盛会的强强联合,将为全球生物科技与医药行业带来前所未有的交流与合作机遇。 生物发酵展作为生物科技领域的知名展会&#x…...

Jenkins 配置 Git Repository 五
Jenkins 配置 Git Repository 五 这里包含了 Freestyle project 任务类型 和 Pipeline 任务类型 关于 Git 仓库的配置,如下 不同的任务类型,只是在不同的模块找到 配置 Git 仓库 找到 Git 仓库配置位置之后,所有的任务类型配置都是一样的 …...

记录阿里云CDN配置
网站接入CDN全流程,共4步!-阿里云开发者社区 1、开通阿里云CDN服务 2、添加加速域名 3、验证域名归属权 4、域名添加CDN生成的CNAME解析 按照官网描述增加。细节点: 1. 域名和泛域名区别 2.开启https,要用nginx的证书,和项…...

mapbox 从入门到精通 - 目录
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:mapbox 从入门到精通 文章目录 一、🍀总目录1.1 ☘️ mapbox基础1.2 ☘️…...

mysql中general_log日志详解
介绍 1.记录范围:这个log里面会记录MySQL所有的SQL语句,不管是查询语句,还是DML语句,还是DDL语句,还是DCL语句,这些语句统统都会被记录在general log文件中。就连我们连接和断开MySQL数据库的这些语句。 2…...

算法与数据结构:从基础到深入
1. 数组 (Array) 定义 一组连续内存空间存储的相同类型元素的集合。特点:通过下标(索引)快速访问元素,但大小固定(静态数组)或可扩展(动态数组)。 核心操作 操作时间复杂度说明访…...

基于千兆5G网关的5G急救车方案
伴随5G网络的全面建成,5G技术的低延时、高速率、广接入等优势,为各行各业都带来了新一轮技术升级。在医疗救援方面,救护车是链接病患与医院的重要纽带,得益于5G物联网的融合应用,救护车也快速向联网化、信息化、智能化…...

【C#】的WPF或是WinForm实现Ctrl+ 的快捷键组合使用
在C#中,无论是WPF还是WinForms应用程序,处理快捷键(例如 Ctrl )通常涉及检测键盘输入并执行相应的命令或方法。 WPF 实现 在WPF中,可以通过设置一个控件的 InputBindings 属性来绑定快捷键。 <Window x:Class&qu…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
