ZOJ 1011 NTA
原题目链接
1011 NTA
NTA(非确定性树自动机)是一种树形结构装置,该装置内置有一套运行规则,通过这些规则,装置可以产生若干个信号,这些信号组成一个信号系统,在这样的系统中,一个信号为起始信号,若干个信号为可接受信号,其余信号为辅助信号。如果一对信号中的两个信号都是可接受的,则称该对信号为可接受对。
这里讨论的树都是二叉树,每个非叶子节点都有两个后继。在任何一棵有限树中,每个节点都有一个信号传递元素。当信号到达一个节点时,信号遇到信号传递物质,引发信号反应,产生多对信号。然后设备非确定性地选择一对信号发送给它的后继。信号对中的第一个信号发送给左边的后继节点,第二个信号发送给右边的后继节点。
NTA 的整个操作如下:
该装置首先向根节点发出起始信号,根据根节点的信号传输物质,非确定性地选择一对信号,将第一对信号发送给左子树,将第二对信号发送给右子树,然后两对信号分别在相应的节点遇到信号传输物质,产生另外两对信号,如此循环往复,直至到达叶子节点。
如果信号到达一个叶子,并且该叶子能够产生一对可接受的信号,我们就说该叶子是“可摇动的”。如果所有叶子都是“可摇动的”,则从根到叶子的信号传输被认为是有效的。如果存在这样的有效传输,则具有信号传输物质的树结构是有效的。如果所有传输都是无效的,则树是无效的。
为简单起见,我们用连续的小写字母“a”、“b”、“c”等表示信号传输元件。NTA 的信号是连续的数字 0、1、2、… 等等。第一个信号 0 始终是起始信号。因此,4 信号 NTA 的信号为“0”、“1”、“2”和“3”。接受信号排列在数字序列的末尾,因此,如果 4 信号 NTA 有两个接受信号,则接受信号为“2”和“3”。信号的转换规则基于转换表。例如,下表描述了具有四个信号“0”、“1”、“2”、“3”和三个信号传输元件“a”、“b”和“c”的转换表。
| T | a | b | c |
|---|---|---|---|
| 0 | (1,2) | (2,1) | (1,0) |
| 1 | (2,2) | (0,2),(1,0) | (3,2) |
| 2 | (2,2) | (2,3) | (1,2) |
| 3 | (1,2) | (2,1) | (3,2) |
在这个转换表中,信号对某些信号传输元件的反应是确定性的,而其他反应则是非确定性的。在上面的例子中,如果信号“1”到达具有传输元件“b”的节点,则反应是非确定性的。
现在你的任务是编写一个程序来判断含有某种信号传递物质的树结构是否有效。
输入
输入文件包含几个案例。每个案例都描述了一系列 NTA 描述和一些初始树配置。每个案例的第一行由三个整数 n、m 和 k 组成。整数 n 表示信号的数量,m 表示接受信号的数量,k 表示信号传输元件的数量。接下来的 nk 行按行主序描述转换表。信号到信号传输元件的每个转换都在单独的一行中给出。在这样的行上,每两个数字代表一个可能的转换。
接下来是树结构的描述。对于每个树结构,在单独的一行中给出一个数字 L,以指示树的级别。接下来的 L+1 行包含字母序列,描述树结构。每行描述一个级别。两个连续字母之间存在一个空格。第 0 级首先开始。在树结构中,空节点用“*”标记。L=-1 的树结构终止该 NTA 的树结构配置,不应判断此结构。
输入以 n=0、m=0 和 k=0 开头的描述结束。不应处理此描述。
注意:在每种情况下,NTA 最多有 l5 个信号和 10 个字符。每棵树的级别不超过 10。
输出
对于每个 NTA 描述,打印 NTA 编号(NTA1、NTA2 等),后跟冒号。然后对于 NTA 的每个初始树配置,打印单词“有效”或“无效”。
在 NTA 案例之间打印空白行。
示例输入
4 2 3
1 2
2 1
1 0
2 2
0 2 1 0
3 2
2 2
2 3
1 2
1 2
2 1
3 2
3
a
b c
a b c b
b a b a c a * *
2
b
a b
b c * *
-1
0 0 0
样本输入的输出
NTA1:
Valid
Invalid
c++代码
#include<bits/stdc++.h>using namespace std;class tree{
public:char val;int code;tree* left;tree* right;tree(char val){this->val = val;this->code = -1;this->left = NULL;this->right = NULL;}
};bool dfs(tree* root, vector<vector<vector<int>>>& trans, int* left, int* right){vector<int> middle = trans[root->code][root->val - 'a'];if (root->left == NULL && root->right == NULL){for (int i = 0; i < middle.size(); i += 2){if (middle[i] >= * left && middle[i] <= *right&& middle[i + 1] >= * left && middle[i + 1] <= * right) return true;}return false;}for (int i = 0; i < middle.size(); i += 2){root->left->code = middle[i];root->right->code = middle[i + 1];bool key1 = false, key2 = false;key1 = dfs(root->left, trans, left, right);if (key1) key2 = dfs(root->right, trans, left, right);if (key1 && key2) return true;}return false;
}int main(){int n, m, k, L, count = 0;while(cin >> n >> m >> k){getchar();count++;if (n == 0 && m == 0 && k == 0) break;vector<vector<vector<int>>> trans(n, vector<vector<int>>(k));for (int i = 0; i < n; i++){for (int j = 0; j < k; j++){while(true){char a = (char)getchar();if (a == '\n') break;if (a == ' ') continue;trans[i][j].push_back(a - '0');}}}if (count != 1) cout << endl;cout << "NTA" << count << ":" << endl;while(cin >> L){getchar();if (L == -1) break;vector<vector<tree*>> roots(L + 1);for (int i = 0; i < L + 1; i++){while(true){char a = (char)getchar();if (a == '\n') break;if (a == ' ') continue;if (a == '*') roots[i].push_back(NULL);else roots[i].push_back(new tree(a));}}for (int i = 0; i < L + 1; i++){int z = roots[i].size();for (int j = 0; j < z; j++){if (i != L && roots[i][j] != NULL){roots[i][j]->left = roots[i + 1][2 * j];roots[i][j]->right = roots[i + 1][2 * j + 1];}}}roots[0][0]->code = 0;int right = n - 1;int left = n - m;if (dfs(roots[0][0], trans, &left , &right)) cout << "Valid" << endl;else cout << "Invalid" << endl;}}return 0;
}//by wqs
题目解析
题目涉及一个名为 NTA(非确定性树自动机)的设备,该设备基于一组转换规则将信号传递下去,最终判断树结构是否有效。具体来说,设备根据信号传递规则,向二叉树的各个节点传递信号,信号传递的有效性取决于每个叶子节点是否能够接受一对“有效的信号对”。
树是一个二叉树,每个非叶子节点有两个子节点。信号传递过程中,从根节点开始传递信号,根节点通过转换规则将信号分发到两个子节点。这个过程会一直递归到叶子节点。
转移规则可以是确定性的(一个信号只能产生一个新的信号对),也可以是非确定性的(一个信号可以产生多个不同的信号对)。
当信号到达叶子节点时,该节点被认为是“可摇动”的,只有当该节点能产生一个有效的信号对(两个信号都为接受信号时),才认为该叶子节点是可摇动的。
如果从根节点到所有叶子节点的信号传递都能满足每个叶子节点的可摇动条件(即每个叶子节点的信号对都为接受信号对),则该树结构是有效的。
否则该树结构为无效。
样例理解
ZOJ 1011 NTA第一个样例解释
ZOJ 1011 NTA 第二个样例解释
实现思路
1、获得转移表
vector<vector<vector<int>>> trans(n, vector<vector<int>>(k));//转移表初始化for (int i = 0; i < n; i++){for (int j = 0; j < k; j++){while(true){char a = (char)getchar();if (a == '\n') break;if (a == ' ') continue;trans[i][j].push_back(a - '0');//获得转移表}}
}
2、创建层序遍历树形数组
输入是按层输入的,根据这个特点可以得出层序遍历树形数组
vector<vector<tree*>> roots(L + 1); //初始化,roots[0]表示第一层结点,roots[1]表示第二层结点,以此类推for (int i = 0; i < L + 1; i++){while(true){char a = (char)getchar();if (a == '\n') break;if (a == ' ') continue;if (a == '*') roots[i].push_back(NULL);else roots[i].push_back(new tree(a));}
}
3、根据层序遍历树形数组创建树形结构
for (int i = 0; i < L + 1; i++){int z = roots[i].size();for (int j = 0; j < z; j++){if (i != L && roots[i][j] != NULL){roots[i][j]->left = roots[i + 1][2 * j];roots[i][j]->right = roots[i + 1][2 * j + 1];}}
}//roots[i][j]的左孩子是roots[i + 1][2 * j],右孩子是roots[i + 1][2 * j + 1]
//这样roots[0][0]就是我们的根节点,已经创建好了
4、深度优先搜索
bool dfs(tree* root, vector<vector<vector<int>>>& trans, int* left, int* right){//root当前根节点,trans转换表,left,right有效信号的区间范围vector<int> middle = trans[root->code][root->val - 'a'];if (root->left == NULL && root->right == NULL){//叶子结点for (int i = 0; i < middle.size(); i += 2){if (middle[i] >= * left && middle[i] <= *right&& middle[i + 1] >= * left && middle[i + 1] <= * right) return true;//只要有一对有效的就是可摇动}return false;//没有一对有效的信号,足以说明此条路,树是无效的}for (int i = 0; i < middle.size(); i += 2){root->left->code = middle[i];root->right->code = middle[i + 1];bool key1 = false, key2 = false;key1 = dfs(root->left, trans, left, right);//判断左子树是否有效if (key1) key2 = dfs(root->right, trans, left, right);//判断右子树是否有效if (key1 && key2) return true;//左子树有效并且右子树有效则这棵树有效}return false;//所有的路这棵树都无效,可以得出这棵树无效
}
相关文章:

ZOJ 1011 NTA
原题目链接 1011 NTA NTA(非确定性树自动机)是一种树形结构装置,该装置内置有一套运行规则,通过这些规则,装置可以产生若干个信号,这些信号组成一个信号系统,在这样的系统中,一个信…...
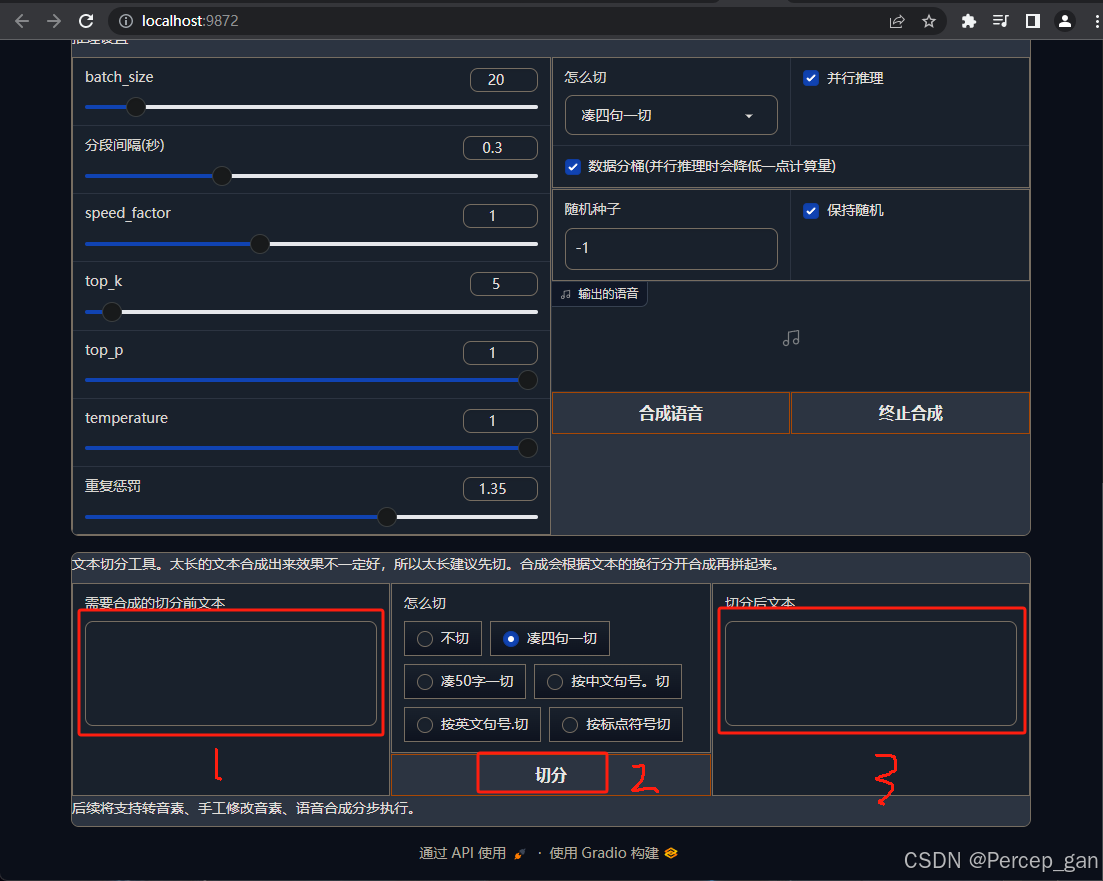
使用 GPT-SoVITS 克隆声音,很详细
使用 GPT-SoVITS 克隆声音,很详细 一、前言二、下载三、启动四、克隆声音1、准备克隆音频2、分离人声伴奏3、音频分割4、语音降噪5、ASR工具6、语音文本校对标注工具7、训练模型8、微调训练9、推理 一、前言 最近对文本转语言很感兴趣,但对直接在网站上…...

Flask和Django相比哪个更适合新手?
Flask 与 Django:哪个更适合新手? 对于新手来说,选择 Flask 还是 Django 主要取决于你的具体需求和项目复杂度。以下是两者的详细对比,帮助你做出选择: 1. Flask 优点 简单易用:Flask 是一个轻量级的微框架,代码简洁,易于理解和上手。适合初学者快速入门。灵活性高:…...

2. 图片性能优化
图片性能优化 图片懒加载 如何判断图片出现在了当前视口 (即如何判断我们能够看到图片)如何控制图片的加载 原生实现 <img src"shanyue.jpg" loading"lazy" />loading"lazy" 延迟加载图像,直到它和视…...

多模态本地部署和ollama部署Llama-Vision实现视觉问答
文章目录 一、模型介绍二、预期用途1. 视觉问答(VQA)与视觉推理2. 文档视觉问答(DocVQA)3. 图像字幕4. 图像-文本检索5. 视觉接地 三、本地部署1. 下载模型2. 模型大小3. 运行代码 四、ollama部署1. 安装ollama2. 安装 Llama 3.2 Vision 模型3. 运行 Llama 3.2-Vision 五、效果…...

cuML机器学习GPU库
cuML安装官网:Installation Guide - RAPIDS Docs 转载:Linux下cuML库的安装与Jupyter集成调试教程-CSDN博客...

机器学习数学基础:24.随机事件与概率
一、教程目标 本教程致力于帮助零基础或基础薄弱的学习者,全面掌握概率论与数理统计的基础公式,透彻理解核心概念,熟练学会应用解题技巧,最终能够轻松应对期末或考研考试。 二、适用人群 特别适合那些对概率论与数理统计知识了…...

CAS单点登录(第7版)27.开发人员
如有疑问,请看视频:CAS单点登录(第7版) 开发人员 Javadocs文档 group org.apereo.cas has published 42 artifact(s) with total 8210 version(s) org.apereo.cas org apereo.cas 小组已出版 42 件作品,共 8210 个版…...

DeepSeek+即梦 做AI视频
DeepSeek做AI视频 制作流程第一步:DeepSeek 生成视频脚本和分镜 第二步:生成分镜图片绘画提示词第三步:生成分镜图片第四步:使用可灵 AI 工具,将生成的图片转成视频。第五步:剪映成短视频 DeepSeek 真的强&…...

OpenMetadata 获取 MySQL 数据库表血缘关系详解
概述 OpenMetadata 是一个开源的元数据管理平台,支持端到端的血缘关系追踪。对于 MySQL 数据库,OpenMetadata 通过解析表的外键约束、视图定义及查询日志(可选)构建表级血缘。本文结合源码分析其实现机制。 环境配置与数据摄取 1. 配置文件示例(YAML) source:type: my…...

计算机组成原理—— 总线系统(十二)
不要害怕失败,因为每一次跌倒都是站起来的前奏;不要畏惧未知,因为在探索的过程中你会发现未曾预见的美好。你的每一步努力都在为未来的成功铺路,即使现在看不到成果,但请相信积累的力量。那些看似平凡的努力࿰…...

详解如何使用Pytest内置Fixture tmp_path 管理临时文件
关注开源优测不迷路 大数据测试过程、策略及挑战 测试框架原理,构建成功的基石 在自动化测试工作之前,你应该知道的10条建议 在自动化测试中,重要的不是工具 临时目录在测试中起着至关重要的作用,它为执行和验证代码提供了一个可控…...

Banana Pi OpenWRT One 官方路由器的第一印象
OpenWRT One是OpenWRT开源社区推出的首款官方开发板,与Banana Pi社区共同设计,由Banana Pi制造和发行。路由器采用蓝色铝合金外壳,质感极佳,视觉效果远超宣传图。整体设计简洁,呈长方形,虽然不是特别时尚&a…...

Golang GORM系列:GORM事务及错误处理
在数据库管理领域,确保数据完整性至关重要。GORM是健壮的Go对象关系映射库,它为开发人员提供了维护数据一致性和优雅地处理错误的基本工具。本文是掌握GORM事务和错误处理的全面指南。我们将深入研究如何使用事务来保证原子性,并探索有效处理…...

NLLB 与 ChatGPT 双向优化:探索翻译模型与语言模型在小语种应用的融合策略
作者:来自 vivo 互联网算法团队- Huang Minghui 本文探讨了 NLLB 翻译模型与 ChatGPT 在小语种应用中的双向优化策略。首先介绍了 NLLB-200 的背景、数据、分词器和模型,以及其与 LLM(Large Language Model)的异同和协同关系。接着…...

ASP.NET Core SixLabors.ImageSharp v1.0 的图像实用程序类 web示例
这个小型实用程序库需要将 NuGet SixLabors.ImageSharp包(版本 1.0.4)添加到.NET Core 3.1/ .NET 6 / .NET 8项目中。它与Windows、Linux和 MacOS兼容。 这已针对 ImageSharp v3.0.1 进行了重新设计。 它可以根据百万像素数或长度乘以宽度来调整图像大…...

ffmpeg configure 研究1-命令行参数的分析
author: hjjdebug date: 2025年 02月 14日 星期五 17:16:12 CST description: ffmpeg configure 研究1 ./configure 命令行参数的分析 文章目录 1 configure 对命令行参数的分析,在4019行1.1 函数名称: is_in1.2. 函数名称: enable1.3. 函数名称: set_all 2 执行退出判断的关键…...

数据结构与算法之排序算法-归并排序
排序算法是数据结构与算法中最基本的算法之一,其作用就是将一些可以比较大小的数据进行有规律的排序,而想要实现这种排序就拥有很多种方法~ 那么我将通过几篇文章,将排序算法中各种算法细化的,详尽的为大家呈现出来: …...

高血压危险因素分析(项目分享)
高血压危险因素分析(项目分享) 高血压作为一种极为常见的慢性疾病,正严重威胁着大众健康。它的发病机制较为复杂,涉及多个方面的因素。 在一份临床采集的数据的基础上,我们通过数据分析手段深入观察一下 BMI…...

java集合框架之Map系列
前言 首先从最常用的HashMap开始。HashMap是基于哈希表实现的,使用数组和链表(或红黑树)的结构。在Java 8之后,当链表长度超过阈值时会转换为红黑树,以提高查询效率。哈希冲突通过链地址法解决。需要明确的是ÿ…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
