【动态规划篇】:当回文串遇上动态规划--如何用二维DP“折叠”字符串?
✨感谢您阅读本篇文章,文章内容是个人学习笔记的整理,如果哪里有误的话还请您指正噢✨
✨ 个人主页:余辉zmh–CSDN博客
✨ 文章所属专栏:动态规划篇–CSDN博客

文章目录
- 一.回文串类DP
- 核心思想(判断所有子串是否是回文子串)
- 二.例题
- 1.回文子串
- 2.最长回文子串
- 3.分割回文串4
- 4.分割回文串2
- 5.最长回文子序列
- 6.让字符串成为回文串的最少插入次数
一.回文串类DP
核心思想(判断所有子串是否是回文子串)
1.状态表示:
定义二维数组dp[i][j],表示字符串s区间[i,j]的子串是否是回文串,其中i位置的字符是子串的起始位置,j位置的字符是子串的结束位置,存储每一个子串的信息,是dp[i][j]为true,不是为false。
2.状态转移方程:
- 如果两端的字符
s[i]==s[j],分为三种情况:- 如果子串长度为1,则下标
i==j,说明字串是一个单独的字符,则一定是回文子串,dp[i][j]=true。 - 如果子串长度为2,则下标
i+1=j,说明子串是两个相邻的字符,并且前提条件两个字符相同,所以也一定是回文子串,dp[i][j]=true。 - 如果子串长度大于2,则下标
j-i>2,需要检查内部区间[i+1,j-1]部分的子串是否是回文子串,如果是并且两端的字符也相等,所以区间[i,j]部分的字串也是回文子串,dp[i][j]=true;如果不是,那区间[i,j]部分的字串也就一定不是回文子串,dp[i][j]=false。
- 如果子串长度为1,则下标
- 如果两端的字符
s[i]!=s[j],则区间[i,j]的子串一定不是回文子串,dp[i][j]=false。
3.初始化:
单个字符一定是回文子串,所以初始值可以设置为true。
4.填表顺序:
根据状态转移方程来决定,当前状态dp[i][j]需要用到前一个状态dp[i+1][j-1],在二维数组中,位于[i,j]位置的左下角,所以填表时,需要从最后一行到第一行,其中每一行按照从左往右的顺序。
因为下标i<=j,所以二维数组中,只需填表斜对角线的上半部分即可。
5.返回值:
需要根据题意来决定。
注意:上面讲解的是关于如何判断所有子串是否是回文子串,并不是每一道的解决步骤都是这样,具体解决方式需要根据题意来决定,但所有的回文串类DP都是在此基础上变形,所以该思想对于解决回文串类DP非常重要。
二.例题
1.回文子串
题目:

算法原理:
题意要求统计所有的回文子串个数,所以可以用二维数组状态表dp[i][j]存储所有子串是否是回文子串的信息,是为true,不是为false。所以最后填完状态表后只需遍历一遍,统计true的个数即可。
代码实现:
int countSubstrings(string s){int n = s.size();//状态表示 dp[i][j]表示以i位置字符为开头,j位置字符为结尾的子串是否是回文子串//状态表中会存储每个子串是否是回文子串的信息vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;//填表顺序 从最后一行到第一行 因为当前状态值需要用到左下角的状态值for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if(s[i]==s[j]){if (i == j || i + 1 == j || dp[i + 1][j - 1] == true){dp[i][j] = true;}}//如果当前子串是回文子串,个数加一if (dp[i][j] == true){ret += 1;}}}//返回值return ret;
}
2.最长回文子串
题目:

算法原理:
题意要求找到最长回文子串并返回,所以在次之前依然需要找到所有的回文子串才能找到最长长度的那个,还是用二维数组状态表dp[i][j]存储所有子串的信息,在填表的时候,如果当前区间的子串是回文子串,就判断是否更新最长长度,注意还要保留最长回文子串的起始位置。
代码实现:
string longestPalindrome(string s){int n = s.size();//状态表示 dp[i][j]表示以i位置字符为开头,j位置字符为结尾的子串是否是回文子串//状态表中会存储每个子串是否是回文子串的信息vector<vector<int>> dp(n, vector<int>(n));int maxlen = 0;int begin = 0;//填表for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if(s[i]==s[j]){if (i == j || i + 1 == j || dp[i + 1][j - 1] == true){dp[i][j] = true;}}if (dp[i][j] == true){//更新最长的长度和开头下标maxlen = max(maxlen, j - i + 1);if (maxlen == j - i + 1){begin = i;}}}}//返回值return s.substr(begin, maxlen);
}
3.分割回文串4
题目:

算法原理:
根据题意要求,需要将原字符串分割成三个回文字符串,所以依然需要知道所有的回文子串,还是用二维数组状态表dp[i][j]存储所有子串的信息。
假设原字符串分成三个区间的字符串,[0,i-1],[i,j],[j+1,n-1]区间,并且i>=1,j<=n-2(因为[0,i-1]区间和[j+1,n-1]区间的字符串至少长度为1),如果存在[i,j]区间的字符串是回文串,并且[0,i-1]区间和[j+1,n-1]的字符串也是回文串,就能分成三个,反之则不存在。
代码实现:
bool checkPartitioning(string s){int n = s.size();//状态表示vector<vector<bool>> dp(n, vector<bool>(n));//填表for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){if (i == j || i + 1 == j || dp[i + 1][j - 1] == true){dp[i][j] = true;}}}}//返回值 分割成三个回文子串 [0,i-1],[i,j],[j+1,n-1]for (int i = 1; i < n - 1; i++){for (int j = i; j < n - 1; j++){if (dp[0][i - 1] == true && dp[i][j] == true && dp[j + 1][n - 1] == true){return true;}}}return false;
}
4.分割回文串2
题目:

算法原理:
根据题意还是需要先知道所有子串是否是回文子串,所以先预处理状态表dp[i][j],找到所有区间的回文子串。
定义一个一维数组min_cut[i]状态表,
状态表示:[0,i]区间内的字符串,分割成回文子串最小的分割次数。
状态转移方程:分为两种情况,
如果[0,i]区间内的字符串已经是回文子串,最小分割次数就为0,min_cut[i]=0;
如果[0,i]区间内的字符串不是回文子串,用下标j遍历区间[0,i],如果区间[j,i]字符串是回文子串,判断区间[0,j-1]的字符串分割成回文子串的最小分割次数,也就是找到min_cut[j-1]的最小值然后加一。
最后返回值就是区间[0,n-1]的字符串分割成回文子串的最小分割数,也就是min_cut[n-1]。
代码实现:
int minCut(string s){int n = s.size();//先获取每个子串是否是回文子串的信息,存放到二维状态表中vector<vector<bool>> dp(n, vector<bool>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){if (i == j || i + 1 == j || dp[i + 1][j - 1] == true){dp[i][j] = true;}}}}//状态表示 min_cut[i]表示[0,i]区间内的子串,分割成回文子串最小的分割次数//初始化 因为要去前状态中的最小值,所以状态表中全部先初始化为最大值vector<int> min_cut(n, INT_MAX);//填表for (int i = 0; i < n; i++){if (dp[0][i] == true){min_cut[i] = 0;}else{for (int j = i; j > 0; j--){if (dp[j][i] == true){//状态转移方程min_cut[i] = min(min_cut[j - 1] + 1, min_cut[i]);}}}}//返回值return min_cut[n - 1];
}
5.最长回文子序列
题目:

算法原理:
本道题有点不同,需要找到的是回文子序列,关键点:回文子序列是允许字符不连续的,因此需要灵活利用状态转移。
状态表示:二维数组dp[i][j],表示s字符串[i,j]区间内,最长回文子序列的长度。
状态转移方程:分为两种情况,
如果两端的字符s[i]==s[j]:
如果下标i==j,说明单独的一个字符表示回文子序列,不存在区间[i+1,j-1],长度直接为1。
如果下标i+1==j,说明两端的字符表示回文子序列,不存在区间[i+1,j-1],长度直接为2。
如果下标j-i>2,可以将这两个字符加入回文子序列的两端,因此找到区间[i+1,j-1]内的最长回文子序列长度然后加2,dp[i][j]=dp[i+1][j-1]+2。
如果两度的字符s[i]!=s[j]:
无法同时包含这两个字符,需要舍弃左端或者右端的字符,然后找剩余区间中的最长回文子序列长度,dp[i][j]=max(dp[i+1][j],dp[i][j-1])。
填表顺序:计算当前状态dp[i][j]的值,需要先知道前三个状态的值,dp[i+1][j-1],dp[i+1][j],dp[i][j-1],在二维数组中分别位于当前位置的左下角,左侧和下侧。因此填表时需要从最后一行到第一行,其中每一行从左往右。
代码实现:
int longestPalindromeSubseq(string s){int n = s.size();//状态表示 dp[i][j]表示[i,j]区间内,最长回文子序列的长度vector<vector<int>> dp(n, vector<int>(n));//填表 从上往下,其中每一行从左往右for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){//如果当前两个位置的字符相等,找区间内的最长回文子序列的长度if (s[i] == s[j]){if (i == j){dp[i][j] = 1;}else if (i + 1 == j){dp[i][j] = 2;}else{dp[i][j] = dp[i + 1][j - 1] + 2;}}//如果当前两个位置的字符不相等,找[i+1,j]和[i,j-1]两个区间内的最长回文子序列的长度else{dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);}}}//返回值return dp[0][n - 1];
}
6.让字符串成为回文串的最少插入次数
题目:

算法原理:
状态表示:二维数组dp[i][j],表示s字符串[i,j]区间内字符串成为回文串的最少插入次数
状态转移方程:分为两种情况,
如果两端的字符s[i]==s[j]:
如果下标i==j,说明单独的一个字符表示长度为1的回文串,不用再插入字符,次数直接为0。
如果下标i+1==j,说明两端的字符表示长度为2的回文串,不用再插入字符,长次数还是为0。
如果下标j-i>2,可以将这两个字符直接加入回文串的两端,因此找到区间[i+1,j-1]内的回文子串最少插入次数,dp[i][j]=dp[i+1][j-1]。
如果两度的字符s[i]!=s[j]:
无法同时包含这两个字符,需要舍弃左端的字符然后在左侧插入一个右端的字符或者舍弃右端的字符然后在右侧插入一个左端的字符,然后找剩余区间中的回文子串最少插入次数,dp[i][j]=max(dp[i+1][j]+1,dp[i][j-1]+1)。
填表顺序:计算当前状态dp[i][j]的值,需要先知道前三个状态的值,dp[i+1][j-1],dp[i+1][j],dp[i][j-1],在二维数组中分别位于当前位置的左下角,左侧和下侧。因此填表时需要从最后一行到第一行,其中每一行从左往右。
代码实现:
int minInsertions(string s){int n = s.size();//状态表示 dp[i][j]表示[i,j]区间内字符串成为回文串的最少插入次数vector<vector<int>> dp(n, vector<int>(n));//填表 从最后一行到第一行,其中每一行从左往右for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){if (i == j || i + 1 == j){dp[i][j] = 0;}else{dp[i][j] = dp[i + 1][j - 1];}}else{dp[i][j] = min(dp[i][j - 1] + 1, dp[i + 1][j] + 1);}}}//返回值return dp[0][n - 1];
}
以上就是关于回文串类DP例题的讲解,如果哪里有错的话,可以在评论区指正,也欢迎大家一起讨论学习,如果对你的学习有帮助的话,点点赞关注支持一下吧!!!

相关文章:

【动态规划篇】:当回文串遇上动态规划--如何用二维DP“折叠”字符串?
✨感谢您阅读本篇文章,文章内容是个人学习笔记的整理,如果哪里有误的话还请您指正噢✨ ✨ 个人主页:余辉zmh–CSDN博客 ✨ 文章所属专栏:动态规划篇–CSDN博客 文章目录 一.回文串类DP核心思想(判断所有子串是否是回文…...

JENKINS(全面)
一.linux系统中JENKINS的安装 注意:安装jenkins需要安装jdk,而且具体版本的jenkins有相对应的jdk版本。可参考以下链接。 Redhat Jenkins 软件包https://pkg.jenkins.io/redhat-stable/https://pkg.jenkins.io/redhat-stable/https://pkg.jenkins.io/r…...

Promise详解大全:介绍、九个方法使用和区别、返回值详解
Promise的介绍 Promise是异步编程的一种解决方案,它的构造函数是同步执行的,then 方法是异步执行的,所以Promise创建后里面的函数会立即执行,构造函数中的resolve和reject只有第一次执行有效,,也就是说Pro…...

尚硅谷爬虫note004
一、urllib库 1. python自带,无需安装 # _*_ coding : utf-8 _*_ # Time : 2025/2/11 09:39 # Author : 20250206-里奥 # File : demo14_urllib # Project : PythonProject10-14#导入urllib.request import urllib.request#使用urllib获取百度首页源码 #1.定义一…...

Debezium系列之:时区转换器,时间戳字段转换到指定时区
Debezium系列之:时区转换器,时间戳字段转换到指定时区 示例:基本配置应用TimezoneConverter SMT的效果示例:高级配置配置选项当Debezium发出事件记录时,记录中的时间戳字段的时区值可能会有所不同,这取决于数据源的类型和配置。为了在数据处理管道和应用程序中保持数据一…...

ubuntu20.04声音设置
step1:打开pavucontrol,设置Configuration和Output Devices, 注意需要有HDMI / DisplayPort (plugged in)这个图标。如果没有,就先选择Configuration -> Digital Stereo (HDMI 7) Output (unplugged) (unvailable),…...

如何设置Python爬虫的User-Agent?
在Python爬虫中设置User-Agent是模拟浏览器行为、避免被目标网站识别为爬虫的重要手段。User-Agent是一个HTTP请求头,用于标识客户端软件(通常是浏览器)的类型和版本信息。通过设置合适的User-Agent,可以提高爬虫的稳定性和成功率…...

深度学习框架探秘|TensorFlow:AI 世界的万能钥匙
在人工智能(AI)蓬勃发展的时代,各种强大的工具和框架如雨后春笋般涌现,而 TensorFlow 无疑是其中最耀眼的明星之一。它不仅被广泛应用于学术界的前沿研究,更是工业界实现 AI 落地的关键技术。今天,就让我们…...

C++:高度平衡二叉搜索树(AVLTree) [数据结构]
目录 一、AVL树 二、AVL树的理解 1.AVL树节点的定义 2.AVL树的插入 2.1更新平衡因子 3.AVL树的旋转 三、AVL的检查 四、完整代码实现 一、AVL树 AVL树是什么?我们对 map / multimap / set / multiset 进行了简单的介绍,可以发现,这几…...

建筑兔零基础自学python记录18|实战人脸识别项目——视频检测07
本次要学视频检测,我们先回顾一下图片的人脸检测建筑兔零基础自学python记录16|实战人脸识别项目——人脸检测05-CSDN博客 我们先把上文中代码复制出来,保留红框的部分。 然后我们来看一下源代码: import cv2 as cvdef face_detect_demo(…...

【MySQL数据库】Ubuntu下的mysql
目录 1,安装mysql数据库 2,mysql默认安装路径 3,my.cnf配置文件? 4,mysql运用的相关指令及说明 5,数据库、表的备份和恢复 mysql是一套给我们提供数据存取的,更加有利于管理数据的服务的网络程序。下…...
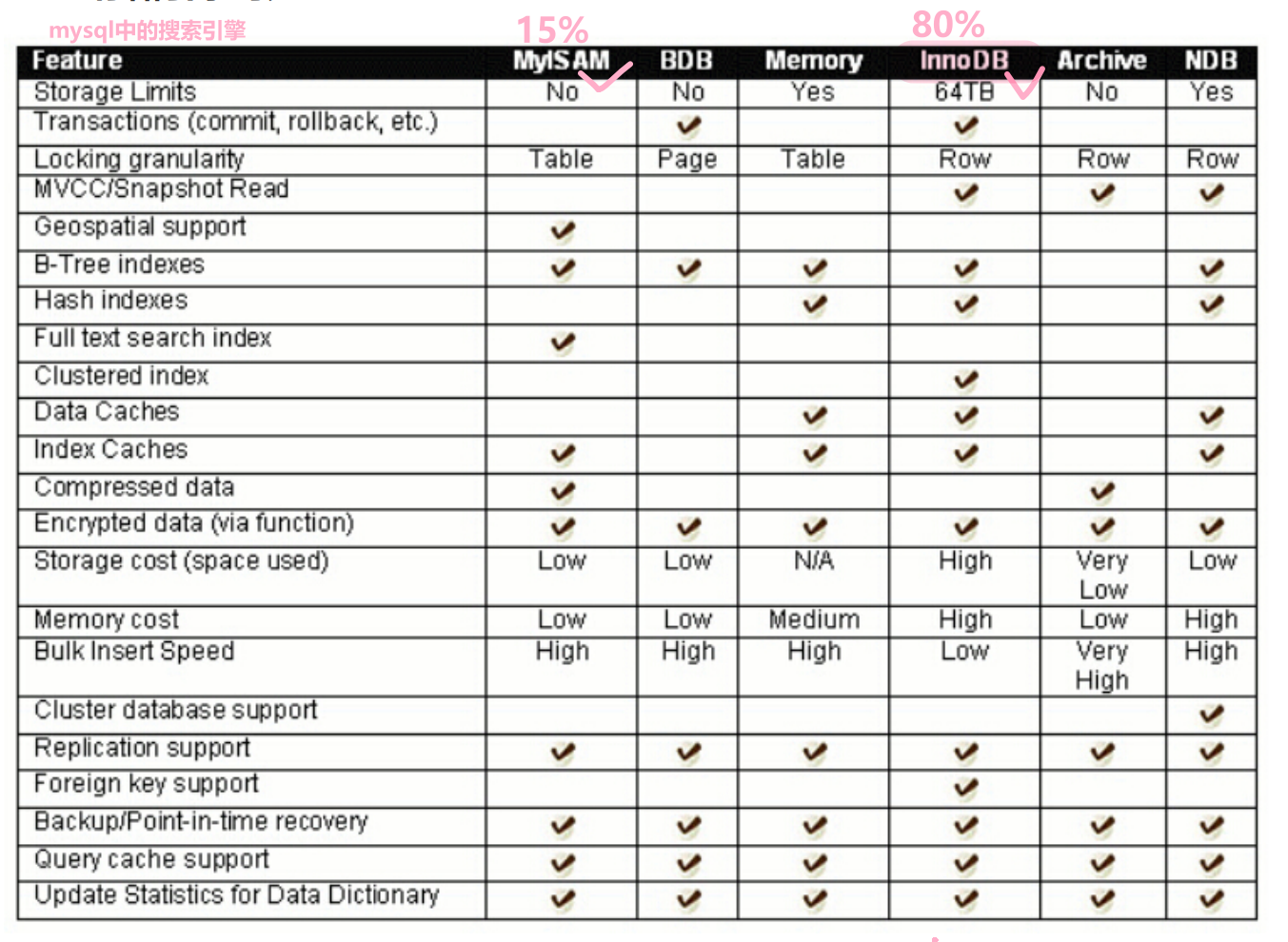
[MySQL#1] database概述 常见的操作指令 MySQL架构 存储引擎
#1024程序员节|征文# 目录 一. 数据库概念 0.连接服务器 1. 什么是数据库 口语中的数据库 为什么数据不直接以文件形式存储,而需要使用数据库呢? 总结 二. ??基础操作 三. 主流数据库 四. 基础知识 服务器,数据库&…...

1.从零开始学会Vue--{{基础指令}}
全新专栏带你快速掌握Vue2Vue3 1.插值表达式{{}} 插值表达式是一种Vue的模板语法 我们可以用插值表达式渲染出Vue提供的数据 1.作用:利用表达式进行插值,渲染到页面中 表达式:是可以被求值的代码,JS引擎会将其计算出一个结果 …...

VS2022中.Net Api + Vue 从创建到发布到IIS
VS2022中.Net Api Vue 从创建到发布到IIS 前言一、先决条件二、创建项目三、运行项目四、增加API五、发布到IIS六、设置Vue的发布 前言 最近从VS2019 升级到了VS2022,终于可以使用官方的.Net Vue 组合了,但是使用过程中还是有很多问题,这里记录一下. 一、先决条件 Visual …...

RFID技术在制造环节的应用与价值
在现代制造业中,信息化和智能化已经成为企业提升竞争力的重要手段。RFID技术因其非接触式、远距离和高效识别的特点,广泛应用于生产的多个环节。本文将详细解读生产过程中RFID的关键应用场景,并结合实际案例,展示其为制造业带来的…...

(前端基础)HTML(一)
前提 W3C:World Wide Web Consortium(万维网联盟) Web技术领域最权威和具有影响力的国际中立性技术标准机构 其中标准包括:机构化标准语言(HTML、XML) 表现标准语言(CSS) 行为标准…...

Linux文件管理:硬链接与软链接
文章目录 1. 硬链接的设计目的(1)节省存储空间(2)提高文件管理效率(3)数据持久性(4)文件系统的自然特性 2. 软链接的设计目的**(1)跨文件系统引用****&#x…...

pnpm, eslint, vue-router4, element-plus, pinia
利用 pnpm 创建 vue3 项目 pnpm 包管理器 - 创建项目 Eslint 配置代码风格(Eslint用于规范纠错,prettier用于美观) 在 设置 中配置保存时自动修复 提交前做代码检查 husky是一个 git hooks工具(git的钩子工具,可以在特定实际执行特…...

在软件产品从开发到上线过程中,不同阶段可能出现哪些问题,导致软件最终出现线上bug
在软件产品从开发到上线的全生命周期中,不同阶段都可能因流程漏洞、技术疏忽或人为因素导致线上问题。以下是各阶段常见问题及典型案例: 1. 需求分析与设计阶段 问题根源:业务逻辑不清晰或设计缺陷 典型问题: 需求文档模糊&#…...

Spring Boot中如何自定义Starter
文章目录 Spring Boot中如何自定义Starter概念和作用1. 概念介绍2. 作用和优势2.1 简化依赖管理2.2 提供开箱即用的自动配置2.3 标准化和模块化开发2.4 提高开发效率2.5 提供灵活的配置覆盖3. 应用场景创建核心依赖1. 确定核心依赖的作用2. 创建 starter-core 模块2.1 依赖管理…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
