C++自研游戏引擎-碰撞检测组件-八叉树AABB检测算法实现
八叉树碰撞检测是一种在三维空间中高效处理物体碰撞检测的算法,其原理可以类比为一个管理三维空间物体的智能系统。这个示例包含两个部分:八叉树部分用于宏观检测,AABB用于微观检测。AABB可以更换为均值或节点检测来提高检测精度。
八叉树的构建
- 确定根节点范围
首先要为整个碰撞检测系统确定一个初始范围,这就像是为所有参与碰撞检测的物体划定一个 “活动区域”。这个范围是一个能够完全容纳所有待检测物体的三维立方体空间,它构成了八叉树的根节点。 - 递归分割空间
为了更高效地管理和查找物体,八叉树会对这个初始的大立方体空间进行递归分割。具体做法是沿着三个坐标轴的中点,将大立方体分割成八个小立方体,每个小立方体对应根节点的一个子节点。之后,系统会检查每个子节点所包含的物体数量:
若某个子节点中的物体数量小于预设的阈值,就认为该区域内的物体分布较为稀疏,无需再进行分割,这些物体就存储在该节点中。
若物体数量超过阈值,说明该区域物体较为密集,需要进一步细分。于是会将这个节点的空间继续分割成八个更小的子空间,并对每个子空间重复上述检查过程,直到满足停止条件。
碰撞检测过程 - 插入物体
在将物体的轴对齐包围盒(AABB)插入八叉树时,系统会从根节点开始判断物体的 AABB 与当前节点的空间是否相交:
如果不相交,表明该物体不在当前节点所管理的空间范围内,无需在此节点存储该物体。
如果相交,则将物体插入当前节点。若当前节点已经被分割成子节点,系统会进一步判断物体的 AABB 与哪个子节点的空间相交,并将物体插入对应的子节点中。 - 查询碰撞
当需要检测某个物体(用其 AABB 表示)是否与其他物体发生碰撞时,系统会从八叉树的根节点开始查询:
若该物体的 AABB 与当前节点的空间不相交,说明该节点及其子节点中的物体都不可能与该物体发生碰撞,无需继续检查该节点及其子树。
若相交,则检查当前节点中存储的物体的 AABB 与该物体的 AABB 是否相交。
若当前节点有子节点,系统会递归地对每个子节点进行相同的查询操作,直到遍历完所有可能发生碰撞的节点。
八叉树碰撞检测的优缺点
优点
高效性:通过对三维空间进行递归分割,八叉树将碰撞检测的范围缩小到可能发生碰撞的区域,避免了对所有物体进行两两比较,从而显著减少了不必要的计算,提高了碰撞检测的效率。在处理大量物体的场景中,这种优势更为明显。
适应性:八叉树能够根据物体在空间中的实际分布情况自适应地进行空间划分,对于物体分布不均匀的场景也能有效地组织和管理物体。
缺点
构建和维护成本较高:构建八叉树需要对空间进行递归分割,并将物体分配到相应的节点中,这需要一定的时间和空间开销。特别是在物体频繁移动或新增、删除物体的场景中,需要不断更新八叉树的结构,增加了维护成本。
存在精度问题:使用 AABB 来近似表示物体可能会导致一定的精度损失,尤其是对于形状复杂的物体,AABB 可能无法精确地描述其外形,从而产生误判。
C++代码
#include <iostream>
#include <vector>
#include <memory>// 定义三维向量结构体
struct Vec3 {float x, y, z;Vec3(float x = 0, float y = 0, float z = 0) : x(x), y(y), z(z) {}
};// 定义 AABB 结构体
struct AABB {Vec3 min;Vec3 max;AABB(const Vec3& min, const Vec3& max) : min(min), max(max) {}// 判断两个 AABB 是否相交bool intersects(const AABB& other) const {return (min.x <= other.max.x && max.x >= other.min.x) &&(min.y <= other.max.y && max.y >= other.min.y) &&(min.z <= other.max.z && max.z >= other.min.z);}
};// 定义八叉树节点类
class OctreeNode {
public:AABB bounds;std::vector<AABB> objects;std::vector<std::unique_ptr<OctreeNode>> children;OctreeNode(const AABB& bounds) : bounds(bounds) {}// 插入 AABB 到节点中void insert(const AABB& object) {if (children.empty()) {if (objects.size() < 8) {objects.push_back(object);} else {split();insert(object);}} else {for (auto& child : children) {if (child->bounds.intersects(object)) {child->insert(object);}}}}// 分割节点void split() {Vec3 center((bounds.min.x + bounds.max.x) / 2, (bounds.min.y + bounds.max.y) / 2, (bounds.min.z + bounds.max.z) / 2);children.resize(8);children[0] = std::make_unique<OctreeNode>(AABB(bounds.min, center));children[1] = std::make_unique<OctreeNode>(AABB(Vec3(center.x, bounds.min.y, bounds.min.z), Vec3(bounds.max.x, center.y, center.z)));children[2] = std::make_unique<OctreeNode>(AABB(Vec3(bounds.min.x, center.y, bounds.min.z), Vec3(center.x, bounds.max.y, center.z)));children[3] = std::make_unique<OctreeNode>(AABB(Vec3(center.x, center.y, bounds.min.z), Vec3(bounds.max.x, bounds.max.y, center.z)));children[4] = std::make_unique<OctreeNode>(AABB(Vec3(bounds.min.x, bounds.min.y, center.z), Vec3(center.x, center.y, bounds.max.z)));children[5] = std::make_unique<OctreeNode>(AABB(Vec3(center.x, bounds.min.y, center.z), Vec3(bounds.max.x, center.y, bounds.max.z)));children[6] = std::make_unique<OctreeNode>(AABB(Vec3(bounds.min.x, center.y, center.z), Vec3(center.x, bounds.max.y, bounds.max.z)));children[7] = std::make_unique<OctreeNode>(AABB(center, bounds.max));for (const auto& object : objects) {for (auto& child : children) {if (child->bounds.intersects(object)) {child->insert(object);}}}objects.clear();}// 检测与指定 AABB 的碰撞void query(const AABB& object, std::vector<AABB>& result) const {if (bounds.intersects(object)) {for (const auto& obj : objects) {if (obj.intersects(object)) {result.push_back(obj);}}for (const auto& child : children) {child->query(object, result);}}}
};// 定义八叉树类
class Octree {
public:std::unique_ptr<OctreeNode> root;Octree(const AABB& bounds) : root(std::make_unique<OctreeNode>(bounds)) {}// 插入 AABB 到八叉树中void insert(const AABB& object) {root->insert(object);}// 检测与指定 AABB 的碰撞std::vector<AABB> query(const AABB& object) const {std::vector<AABB> result;root->query(object, result);return result;}
};// 示例使用
int main() {// 定义八叉树的边界AABB octreeBounds(Vec3(0, 0, 0), Vec3(100, 100, 100));Octree octree(octreeBounds);// 插入一些 AABBoctree.insert(AABB(Vec3(10, 10, 10), Vec3(20, 20, 20)));octree.insert(AABB(Vec3(30, 30, 30), Vec3(40, 40, 40)));// 定义一个查询的 AABBAABB queryAABB(Vec3(15, 15, 15), Vec3(25, 25, 25));// 进行碰撞检测std::vector<AABB> collisions = octree.query(queryAABB);// 输出碰撞结果std::cout << "Collisions found: " << collisions.size() << std::endl;for (const auto& collision : collisions) {std::cout << "Collision: min(" << collision.min.x << ", " << collision.min.y << ", " << collision.min.z << "), max("<< collision.max.x << ", " << collision.max.y << ", " << collision.max.z << ")" << std::endl;}return 0;
}
相关文章:

C++自研游戏引擎-碰撞检测组件-八叉树AABB检测算法实现
八叉树碰撞检测是一种在三维空间中高效处理物体碰撞检测的算法,其原理可以类比为一个管理三维空间物体的智能系统。这个示例包含两个部分:八叉树部分用于宏观检测,AABB用于微观检测。AABB可以更换为均值或节点检测来提高检测精度。 八叉树的…...

spring boot对接clerk 实现用户信息获取
在现代Web应用中,用户身份验证和管理是一个关键的功能。Clerk是一个提供身份验证和用户管理的服务,可以帮助开发者快速集成这些功能。在本文中,我们将介绍如何使用Spring Boot对接Clerk,以实现用户信息的获取。 1.介绍 Clerk提供…...

一种动态地址的查询
背景 当我们注入一个进程,通过函数地址进行call时经常会遇到这样的一个问题。对方程序每周四会自动更新。更新后之前的函数地址就变化了,然后需要重新找地址。所以,我就使用了一个动态查询的方式。 第一步:先为需要call的函数生…...

周雨彤:用角色与生活,诠释审美的艺术
提到内娱审美优秀且持续在线的女演员,周雨彤绝对是其中最有代表性的一个。 独树一帜的表演美学 作为新生代演员中的实力派代表,周雨彤凭借细腻的表演和对角色的深度共情,在荧幕上留下了多个令人难忘的“出圈”形象。在《我在他乡挺好的》中…...

使用jks给空apk包签名
1、在平台官方下载空的apk包(上传应用时有提醒下载) 2、找到jdk目录,比如C:\Program Files\Java\jdk1.8\bin,并把下载的空包apk和jks文件放到bin下 3、以管理员身份运行cmd,如果不是管理员会签名失败 4、用cd定位到…...

500. 键盘行 771. 宝石与石头 简单 find接口的使用
500. 键盘行1 给你一个字符串数组 words ,只返回可以使用在 美式键盘 同一行的字母打印出来的单词。键盘如下图所示。 请注意,字符串 不区分大小写,相同字母的大小写形式都被视为在同一行。 美式键盘 中: 第一行由字符 "qwer…...

仙剑世界手游新手攻略 仙剑世界能用云手机玩吗
欢迎来到《仙剑世界》手游的仙侠世界!作为新手玩家,以下是一些详细的攻略和建议,帮助你快速上手并享受游戏的乐趣。 一、新手职业推荐 1.轩辕:这是一个偏辅助的职业,可以给队友提供输出加成等增益效果,不过…...

[题解]2024CCPC重庆站-小 C 的神秘图形
Sources:K - 小 C 的神秘图形Abstract:给定正整数 n ( 1 ≤ n ≤ 1 0 5 ) n(1\le n\le 10^5) n(1≤n≤105),三进制字符串 n 1 , n 2 ( ∣ n 1 ∣ ∣ n 2 ∣ n ) n_1,n_2(|n_1||n_2|n) n1,n2(∣n1∣∣n2∣n),按如下方法…...
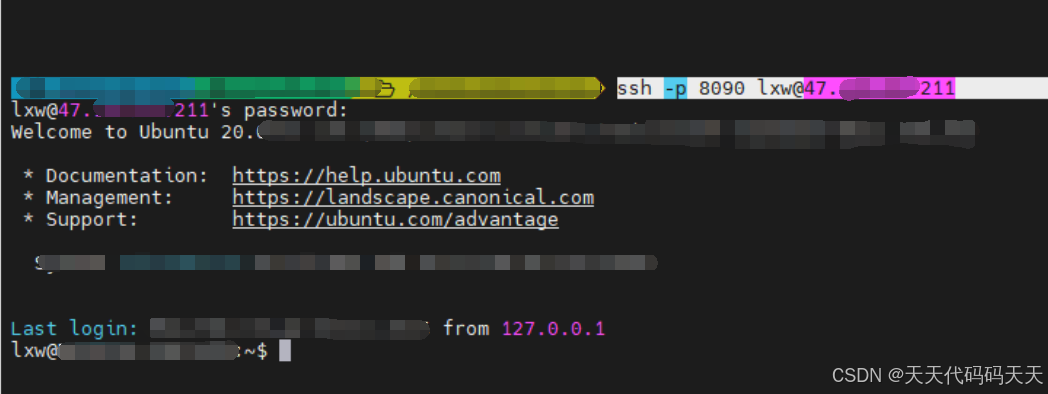
NPS内网穿透SSH使用手册
1、说明 nps-一款轻量级、高性能、功能强大的内网穿透代理服务器 github地址:https://github.com/ehang-io/nps 官网文档地址:https://ehang-io.github.io/nps/#/?idnps 2、服务端 下载地址:https://github.com/ehang-io/nps/releases 下…...
大幂计算和大阶乘计算【C语言】
大幂计算: #include<stdio.h> long long int c[1000000]{0}; int main() {long long a,b,x1;c[0]1;printf("请输入底数:");scanf("%lld",&a);printf("请输入指数:");scanf("%lld",&b…...

【Linux】详谈 进程控制
目录 一、进程是什么 二、task_struct 三、查看进程 四、创建进程 4.1 fork函数的认识 4.2 2. fork函数的返回值 五、进程终止 5.1. 进程退出的场景 5.2. 进程常见的退出方法 5.2.1 从main返回 5.2.1.1 错误码 5.2.2 exit函数 5.2.3 _exit函数 5.2.4 缓冲区问题补…...

Linux top 命令
作用 top 是一个实时系统监控工具,用于查看系统的资源使用情况和进程状态。 示例 以下是一些常用的 top 命令示例: top :动态显示结果,每 3 秒刷新一次。 top -d 2:动态显示结果,每 2 秒刷新一次。 top …...

Leetcode 424-替换后的最长重复字符
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。 在执行上述操作后,返回 包含相同字母的最长子字符串的长度。 题解 可以先做LCR 167/Leetcode 03再做本题 滑动窗口&…...

《StyleDiffusion:通过扩散模型实现可控的解耦风格迁移》学习笔记
paper:2308.07863 目录 摘要 1、介绍 2、相关工作 2.1 神经风格迁移(NST) 2.2 解耦表示学习(DRL) 2.3 扩散模型(Diffusion Models) 3、方法 3.1 风格移除模块 3.2 风格转移模块 3.3 …...

Django 创建表时 “__str__ ”方法的使用
在 Django 模型中,__str__ 方法是一个 Python 特殊方法(也称为“魔术方法”),用于定义对象的字符串表示形式。它的作用是控制当对象被转换为字符串时,应该返回什么样的内容。 示例: 我在初学ModelForm时尝…...

图像处理之CSC
CSC 是 Color Space Conversion(色彩空间转换)的缩写,它涉及图像处理中的亮度、饱和度、对比度和色度等参数的调整。这些参数是图像处理中的核心概念,通常用于描述和操作图像的颜色信息。 以下是亮度、饱和度、对比度和色度与 CS…...

C语言数组之二维数组
C语言 主要内容 数组 二维数组 数组 二维数组 定义 二维数组本质上是一个行列式的组合,也就是说二维数组由行和列两部分组成,属于多维数组。二维数组数据是通过行列进行解读。二维数组可被视为一个特殊的一维数组,相当于二维数组又是一…...

PyTorch 源码学习:阅读经验 代码结构
分享自己在学习 PyTorch 源码时阅读过的资料。本文重点关注阅读 PyTorch 源码的经验和 PyTorch 的代码结构。因为 PyTorch 不同版本的源码实现有所不同,所以笔者在整理资料时尽可能按版本号升序,版本号见标题前[]。最新版本的源码实现还请查看 PyTorch 仓…...

vite+vue3开发低版本浏览器不支持es6语法的问题排坑笔记
重要提示:请首先完整阅读完文章内容后再操作,以免不必要的时间浪费!切记!!!在使用vitevue3开发unapp项目时,发现低版本浏览器不兼容es6的语法,如“?.” “??” 等,为了…...
函数,格式输出符)
C语言中printf()函数,格式输出符
在 C 语言中,printf() 函数的格式输出符(格式说明符)用于控制输出的格式和数据类型。以下是常见的格式说明符及其用法: 基本格式符 打印各种类型的值 格式输出符数据类型说明%dint输出有符号十进制整数%uunsigned int输出无符号…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

VSCode 没有添加Windows右键菜单
关键字:VSCode;Windows右键菜单;注册表。 文章目录 前言一、工程环境二、配置流程1.右键文件打开2.右键文件夹打开3.右键空白处打开文件夹 三、测试总结 前言 安装 VSCode 时没有注意,实际使用的时候发现 VSCode 在 Windows 菜单栏…...
