【时间复杂度和空间复杂度】
常见的时间复杂度
计算方法1、确定输入规模:
输入规模通常用 n 表示,例如数组长度、链表长度等。2、分析算法的执行步骤:
计算每个操作的执行次数。
确定操作的执行次数与输入规模的关系。3、忽略常数和低阶项:
在大O表示法中,常数和低阶项可以忽略,只保留最高阶项。
例如,O(3n² + 2n + 1) 简化为 O(n²)。举例:
假设有一个算法,其执行步骤如下:arr = [1, 2, 3, 4, 5]
for i in arr: # O(n)for j in arr: # O(n)print(i, j)外层循环:执行 n 次。
内层循环:每次外层循环执行 n 次。
总执行次数:n * n = n²。
时间复杂度:O(n²)。
-
O(1):常数时间复杂度
-
不论输入规模如何,算法的执行时间是固定的。
-
示例:访问数组的某个元素。
arr = [1, 2, 3] print(arr[1]) # 时间复杂度为 O(1)
-
-
O(n):线性时间复杂度
-
算法的执行时间与输入规模成正比。
-
示例:遍历一个数组。
arr = [1, 2, 3, 4, 5] for i in arr:print(i) # 时间复杂度为 O(n)
-
-
O(n²):二次时间复杂度
-
算法的执行时间与输入规模的平方成正比。
-
示例:嵌套循环。
arr = [1, 2, 3, 4, 5] for i in arr:for j in arr:print(i, j) # 时间复杂度为 O(n²)
-
-
O(log n):对数时间复杂度
-
算法的执行时间与输入规模的对数成正比。
-
示例:二分查找。
def binary_search(arr, target):left, right = 0, len(arr) - 1while left <= right:mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] < target:left = mid + 1else:right = mid - 1return -1 # 时间复杂度为 O(log n)
-
-
O(n log n):线性对数时间复杂度
-
算法的执行时间与输入规模的对数成正比。
-
示例:快速排序、归并排序。
def merge_sort(arr):if len(arr) <= 1:return arrmid = len(arr) // 2left = merge_sort(arr[:mid])right = merge_sort(arr[mid:])return merge(left, right) # 时间复杂度为 O(n log n)
-
空间复杂度
定义:空间复杂度是指算法在运行过程中消耗的内存资源量级,通常用输入规模(如数组长度、链表长度等)来表示。
表示方法:空间复杂度也用大O符号(O)表示,例如 O(1)、O(n)、O(n²) 等。
计算方法1)确定输入规模:
输入规模通常用 n 表示,例如数组长度、链表长度等。2)分析算法使用的额外内存:
计算算法中使用的额外空间(如变量、数组、递归栈等)。
确定额外空间的使用量与输入规模的关系。3)忽略常数和低阶项:
在大O表示法中,常数和低阶项可以忽略,只保留最高阶项。
例如,O(3n² + 2n + 1) 简化为 O(n²)。
假设有一个算法,其执行步骤如下:
Python复制
def merge_sort(arr):if len(arr) <= 1:return arrmid = len(arr) // 2left = merge_sort(arr[:mid]) # 创建左半部分数组right = merge_sort(arr[mid:]) # 创建右半部分数组return merge(left, right) # 合并两个数组-
递归调用:每次递归调用会创建两个子数组。
-
空间复杂度:
-
每次递归调用创建的子数组占用 O(n) 的空间。
-
递归深度为 O(log n)。
-
总空间复杂度为 O(n)(递归栈空间)。
-
常见的空间复杂度
-
O(1):常数空间复杂度
-
不论输入规模如何,算法使用的额外内存是固定的。
-
示例:交换两个变量的值。
a, b = 1, 2 a, b = b, a # 空间复杂度为 O(1)
-
-
O(n):线性空间复杂度
-
算法使用的额外内存量与输入规模成正比。
-
示例:复制一个数组。
arr = [1, 2, 3, 4, 5] new_arr = arr[:] # 空间复杂度为 O(n)
-
-
O(n²):二次空间复杂度
-
算法使用的额外内存量与输入规模的平方成正比。
-
示例:创建一个二维数组。
arr = [[0] * n for _ in range(n)] # 空间复杂度为 O(n²)
-
相关文章:

【时间复杂度和空间复杂度】
常见的时间复杂度 计算方法1、确定输入规模: 输入规模通常用 n 表示,例如数组长度、链表长度等。2、分析算法的执行步骤: 计算每个操作的执行次数。 确定操作的执行次数与输入规模的关系。3、忽略常数和低阶项: 在大O表示法中&am…...

王炸 用AI+飞书 分解 一键生成 项目计划表模版
效果图: 各字段设置: 以下是一个使用 AI(DeepSeeker) 飞书多维表格分解项目待办模板的示例,你可以根据实际情况进行调整和优化: 列表中需要选择对象,且选择输出结果(记得控制字符长度…...

VisionMaster4.4 python脚本 图像处理 转换函数 爱之初体验
最近有接触过一丢丢VM4.3的模块开发. 一直有把python图像处理部分模块移植进来的打算 不过时间不够没来得及折腾.偶尔发现4.4支持py脚本 于是拿来折腾.一下午. 发现4.4支持python脚本,好开心. 首先安装VM4.4 注意一定要是4.4 打开后拖了一个模块. 但是发现import numpy imp…...

线程池的使用 + MD5加密 + 枚举类
文章目录 1、线程池的使用2、MD5算法的使用3、多用枚举类 整理下近期干活儿遇到的一些坑。 1、线程池的使用 不合理点1:jstack线程转储发现,有几万个线程,查看代码发现,线程池放在方法内部或者循环体中创建,尽管方法…...

[qt5学习笔记]Application Example示例程序源码解析
开发环境问题 vs2022下直接打开ui、ts文件失败 解决办法如下图, 设置designer独立运行。估计是嵌入运行存在些许bug。 同理,ts编辑工具linguist也存在这个问题。 qrc rc的编辑嵌入编辑都正常,但分离式更稳定可靠。 qt creator编译失败 原…...

【在时光的棋局中修行——论股市投资的诗意哲学】
在时光的棋局中修行——论股市投资的诗意哲学 引子:数字之海与星辰之约 在经纬交织的K线图里,我常看见银河倾泻的轨迹。那些跳动的数字如同繁星坠落,在午夜时分编织着财富的密码。炒股之道,是理性与诗意的交响,是数据…...

IB网络错误检查工具ibqueryerrors
ibqueryerrors 是一个用于查询 InfiniBand 网络中错误统计信息的工具。它可以帮助网络管理员识别和诊断网络问题,如丢包、重传和其他通信错误。这个工具通常是 InfiniBand 管理软件包的一部分,例如 OpenSM(Open Subnet Manager)。…...
「vue3-element-admin」Vue3 + TypeScript 项目整合 Animate.css 动画效果实战指南
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall ︱vue3-element-admin︱youlai-boot︱vue-uniapp-template 🌺 仓库主页: GitCode︱ Gitee ︱ Github 💖 欢迎点赞 👍 收藏 ⭐评论 …...

论文阅读 DOES END-TO-END AUTONOMOUS DRIVING REALLY NEED PERCEPTION TASKS?
端到端的强势来袭,好久了~~~ 简单翻译:端到端真的需要感知任务嘛? code https://github.com/PeidongLi/SSR. https://arxiv.org/pdf/2409.18341 1. 摘要 端到端自动驾驶(E2EAD)方法通常依赖于监督式感知任务来提取显…...
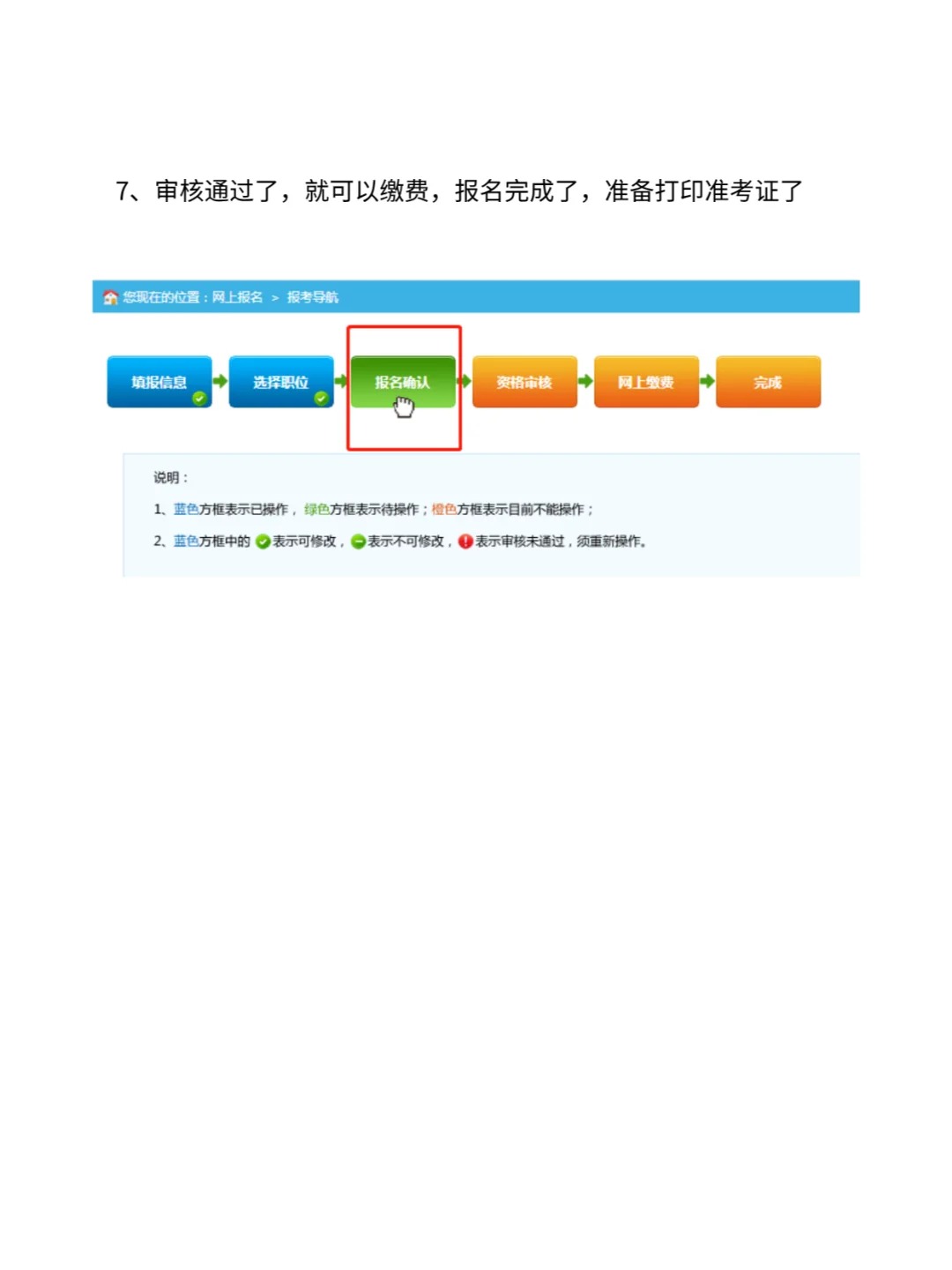
25年黑龙江省考报名流程详细教程
2025年黑龙江省考报名马上就要开始报名啦! 有想要参加黑龙江省考报名的同学,可以提前了解一下考试报名流程,熟悉考试报名照要求! 一、考试时间安排 报名时间:2月18日9:00至2月23日17:00 缴费时间:2月18日…...

基于SpringBoot的小区运动中心预约管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

部署postgresql_exporter监控pgsql
部署exporter配置监控job配置告警规则 一键部署脚本 #!/bin/bash# 定义变量 PG_HOST"xx.ap-southeast-1.rds.amazonaws.com" PG_PORT"5432" PG_PASSWORD"bagayalu321" PG_USER"monitor_user" EXPORTER_VERSION"0.16.0" #…...

Mac本地部署deepseek
Ollama 运行deepseek需要本地运行工具ollama,安装路径如下 ollama官方网站 (https://ollama.com/download) 下载Mac版ollama,点击移至application下面 DeepSeek R1 14b 通过ollama安装deepseek,对应的运行指令可通过 deepseek本地部署列表…...

huggingface+下载deepseek8b lamda+本地部署 笔记
步骤倒过来 1.python hf_download.py --model unsloth/DeepSeek-R1-Distill-Llama-8B-GGUF model后加模型名(HF-Mirror中查) 【huggingface模型下载不下来?这里教你万能解决办法~huggingface小白使用指南。】 https://www.bilibili.com/video…...

中上211硕对嵌入式AI感兴趣,如何有效规划学习路径?
今天给大家分享的是一位粉丝的提问,中上211硕对嵌入式AI感兴趣,如何有效规划学习路径? 接下来把粉丝的具体提问和我的回复分享给大家,希望也能给一些类似情况的小伙伴一些启发和帮助。 同学提问: 中上211,…...

Jedis 客户端 用于java连接redis服务
<dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId...

车载诊断数据库 --- 通用性诊断数据库ODX
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 简单,单纯,喜欢独处,独来独往,不易合同频过着接地气的生活,除了生存温饱问题之外,没有什么过多的欲望,表面看起来很高冷,内心热情,如果你身…...
)
docker 基础命令使用(ubuntu)
docker 状态查询 docker ps docker ps -adocker --version docker info docker --help docker run --help docker ps --help ...docker 操作镜像命令 docker imagesdocker rmi 镜像id/镜像名docker 操作容器命令 docker ps docker ps -adocker run 命令 # 端口映射 -p 参数…...

IDEA集成DeepSeek
引言 随着数据量的爆炸式增长,传统搜索技术已无法满足用户对精准、高效搜索的需求。 DeepSeek作为新一代智能搜索技术,凭借其强大的语义理解与深度学习能力,正在改变搜索领域的游戏规则。 对于 Java 开发者而言,将 DeepSeek 集成…...

Unity 接入Luabn记录图解
Luban 文档及链接项目目录UnityEditor 导表工具 文档及链接 官方文档 最新版本 项目目录 接入的方法有很多,我这里随便找了一种 https://gitee.com/focus-creative-games/luban_examples.git如上图,git拉去后,只保留圈起来的2个文件夹。…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
