机器学习_13 决策树知识总结
决策树是一种直观且强大的机器学习算法,广泛应用于分类和回归任务。它通过树状结构的决策规则来建模数据,易于理解和解释。今天,我们就来深入探讨决策树的原理、实现和应用。
一、决策树的基本概念
1.1 决策树的工作原理
决策树是一种基于树结构的模型,通过一系列的决策规则将数据划分为不同的类别或预测目标值。它的基本工作流程如下:
-
根节点:从整个数据集开始。
-
分支节点:根据某个特征的值将数据集分割成多个子集。
-
叶子节点:最终的预测结果,包含类别标签(分类问题)或目标值(回归问题)。
-
预测:对于新样本,从根节点开始,根据特征值沿着树的分支向下遍历,直到到达叶子节点,叶子节点的值即为预测结果。
1.2 决策树的优势
-
易于理解和解释:决策树的规则直观,易于可视化。
-
处理多种数据类型:可以处理数值型和分类型数据。
-
无需特征缩放:对特征的尺度不敏感,不需要进行标准化或归一化。
1.3 决策树的局限性
-
容易过拟合:如果树的深度过大,可能会过度拟合训练数据,导致泛化能力差。
-
对数据敏感:对数据中的噪声和异常值较为敏感。
-
计算复杂度高:尤其是当特征数量较多时,训练时间可能会较长。
二、决策树的构建与划分准则
2.1 划分准则
在构建决策树时,选择合适的划分准则至关重要。常见的划分准则包括:
-
信息增益(Information Gain):基于信息论的概念,选择使熵(Entropy)减少最多的特征进行划分。信息增益越大,表示划分后的数据更加纯净。
-
基尼不纯度(Gini Impurity):衡量节点的纯度,选择使基尼不纯度降低最多的特征进行划分。基尼不纯度越低,表示节点的纯度越高。
-
均方误差(Mean Squared Error, MSE):用于回归问题,选择使均方误差最小的特征进行划分。
2.2 如何选择最佳划分准则
-
信息增益:偏向于选择取值较多的特征,适合特征数量较少的情况。
-
基尼不纯度:计算简单,适合处理多分类问题,对特征的选择较为平衡。
-
均方误差:适用于回归问题,能够有效衡量预测值与真实值之间的差异。
三、决策树的实现与案例
3.1 Python实现
以下是使用Python和Scikit-Learn库实现决策树分类的代码示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target# 创建并拟合决策树分类器
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X, y)# 可视化决策树
plt.figure(figsize=(12, 8))
tree.plot_tree(clf,feature_names=iris.feature_names,class_names=iris.target_names.tolist(),filled=True,rounded=True)
plt.show()3.2 案例分析
假设我们有一组数据,记录了患者的年龄、性别、症状和是否患有某种疾病。我们希望通过决策树模型预测患者是否患病。
-
数据准备:收集患者的年龄、性别、症状等特征,以及是否患病的标签。
-
模型训练:使用决策树分类器拟合数据,选择合适的划分准则(如基尼不纯度)。
-
模型评估:通过可视化决策树,理解模型的决策规则;计算准确率、召回率等指标,评估模型性能。
-
预测应用:根据模型预测新患者的患病概率,为医疗诊断提供参考。
四、决策树的优化与剪枝
4.1 过拟合问题
决策树容易过拟合,尤其是在树的深度较大时。为了避免过拟合,可以采取以下方法:
-
限制树的深度:设置最大深度参数(
max_depth),控制树的生长。 -
增加最小样本数:设置每个叶子节点的最小样本数(
min_samples_leaf)和分裂节点的最小样本数(min_samples_split),防止过度细分。 -
剪枝:通过剪枝操作减少树的复杂度,提高泛化能力。
4.2 剪枝方法
-
预剪枝(Pre-pruning):在树生长过程中提前停止,例如设置最大深度或最小样本数。
-
后剪枝(Post-pruning):先让树完全生长,然后剪掉一些分支。常见的后剪枝方法包括成本复杂度剪枝(Cost-Complexity Pruning)。
五、决策树的评估指标
5.1 常用评估指标
-
准确率(Accuracy):预测正确的样本数占总样本数的比例。
-
精确率(Precision):预测为正类的样本中实际为正类的比例。
-
召回率(Recall):实际为正类的样本中预测为正类的比例。
-
F1分数:精确率和召回率的调和平均值,综合考虑了精确率和召回率。
通过这些评估指标,我们可以全面地评价决策树模型的性能,选择最适合问题的模型。
👏觉得文章对自己有用的宝子可以收藏文章并给小编点个赞!
👏想了解更多统计学、数据分析、数据开发、数据治理、机器学习算法、深度学习等有关知识的宝子们,可以关注小编,希望以后我们一起成长!
相关文章:

机器学习_13 决策树知识总结
决策树是一种直观且强大的机器学习算法,广泛应用于分类和回归任务。它通过树状结构的决策规则来建模数据,易于理解和解释。今天,我们就来深入探讨决策树的原理、实现和应用。 一、决策树的基本概念 1.1 决策树的工作原理 决策树是一种基于…...

请解释一下Standford Alpaca格式、sharegpt数据格式-------deepseek问答记录
1 Standford Alpaca格式 json格式数据。Stanford Alpaca 格式是一种用于训练和评估自然语言处理(NLP)模型的数据格式,特别是在指令跟随任务中。它由斯坦福大学的研究团队开发,旨在帮助模型理解和执行自然语言指令。以下是该格式的…...

ubuntu 安装管理多版本python3 相关问题解决
背景:使用ubuntu 22.04 默认python 未3.10.编译一些模块的时候发现需要降级到python3.9.于是下载安装 下载: wget https://www.python.org/ftp/python/3.9.16/Python-3.9.16.tgz解压与编译 tar -xf Python-3.9.16.tgz cd Python-3.9.16 ./configure -…...

滑动窗口算法篇:连续子区间与子串问题
1.滑动窗口原理 那么一谈到子区间的问题,我们可能会想到我们可以用我们的前缀和来应用子区间问题,但是这里对于子区间乃至子串问题,我们也可以尝试往滑动窗口的思路方向去进行一个尝试,那么说那么半天,滑动窗口是什么…...

Python爬虫实战:股票分时数据抓取与存储 (1)
在金融数据分析中,股票分时数据是投资者和分析师的重要资源。它能够帮助我们了解股票在交易日内的价格波动情况,从而为交易决策提供依据。然而,获取这些数据往往需要借助专业的金融数据平台,其成本较高。幸运的是,通过…...

【设计模式】【行为型模式】访问者模式(Visitor)
👋hi,我不是一名外包公司的员工,也不会偷吃茶水间的零食,我的梦想是能写高端CRUD 🔥 2025本人正在沉淀中… 博客更新速度 👍 欢迎点赞、收藏、关注,跟上我的更新节奏 🎵 当你的天空突…...

基于实例详解pytest钩子pytest_generate_tests动态生成测试的全过程
关注开源优测不迷路 大数据测试过程、策略及挑战 测试框架原理,构建成功的基石 在自动化测试工作之前,你应该知道的10条建议 在自动化测试中,重要的不是工具 作为一名软件开发人员,你一定深知有效测试策略的重要性,尤其…...

Copilot基于企业PPT模板生成演示文稿
关于copilot创建PPT,咱们写过较多文章了: Copilot for PowerPoint通过文件创建PPT Copilot如何将word文稿一键转为PPT Copilot一键将PDF转为PPT,治好了我的精神内耗 测评Copilot和ChatGPT-4o从PDF创建PPT功能 Copilot for PPT全新功能&a…...

2025百度快排技术分析:模拟点击与发包算法的背后原理
一晃做SEO已经15年了,2025年还有人问我如何做百度快速排名,我能给出的答案就是:做好内容的前提下,多刷刷吧!百度的SEO排名算法一直是众多SEO从业者研究的重点,模拟算法、点击算法和发包算法是百度快速排名的…...

七星棋牌全开源修复版源码解析:6端兼容,200种玩法全面支持
本篇文章将详细讲解 七星棋牌修复版源码 的 技术架构、功能实现、二次开发思路、搭建教程 等内容,助您快速掌握该棋牌系统的开发技巧。 1. 七星棋牌源码概述 七星棋牌修复版源码是一款高度自由的 开源棋牌项目,该版本修复了原版中的多个 系统漏洞&#…...

解锁原型模式:Java 中的高效对象创建之道
系列文章目录 后续补充~~~ 文章目录 一、引言1.1 软件开发中的对象创建困境1.2 原型模式的登场 二、原型模式的核心概念2.1 定义与概念2.2 工作原理剖析2.3 与其他创建型模式的差异 三、原型模式的结构与角色3.1 抽象原型角色3.2 具体原型角色3.3 客户端角色3.4 原型管理器角色…...

DeepSeek从入门到精通:揭秘 AI 提示语设计误区与 AI 幻觉(新手避坑指南)
文章目录 引言常见陷阱与应对策略:新手必知的提示词设计误区缺乏迭代陷阱:期待一次性完美结果过度指令与模糊指令陷阱:当细节缺乏重点或意图不明确假设偏见陷阱:当前 AI 只听你想听的幻觉生成陷阱:当AI自信地胡说八道忽…...

Jenkins同一个项目不同分支指定不同JAVA环境
背景 一些系统应用,会为了适配不同的平台,导致不同的分支下用的是不同的gradle,导致需要不同的JAVA环境来编译,比如a分支需要使用JAVA11, b分支使用JAVA17。 但是jenkins上,一般都是Global Tool Configuration 全局所有环境公用一个JAVA_HOME。 尝试过用 Build 的Execut…...
从入门到精通:Postman 实用指南
Postman 是一款超棒的 API 开发工具,能用来测试、调试和管理 API,大大提升开发效率。下面就给大家详细讲讲它的安装、使用方法,再分享些实用技巧。 一、安装 Postman 你能在 Postman 官网(https://www.postman.com )下…...

win32汇编环境,对话框中使用月历控件示例二
;运行效果 ;win32汇编环境,对话框中使用月历控件示例二 ;以下示例有2个操作,即将每周的开始日进行改变,将默认的周日开始改为周一开始,同时实现点击哪个日期,则设定为哪个日期 ;直接抄进RadAsm可编译运行。重要部分加备注。 ;下面为asm文件 ;>>>>>>>&…...
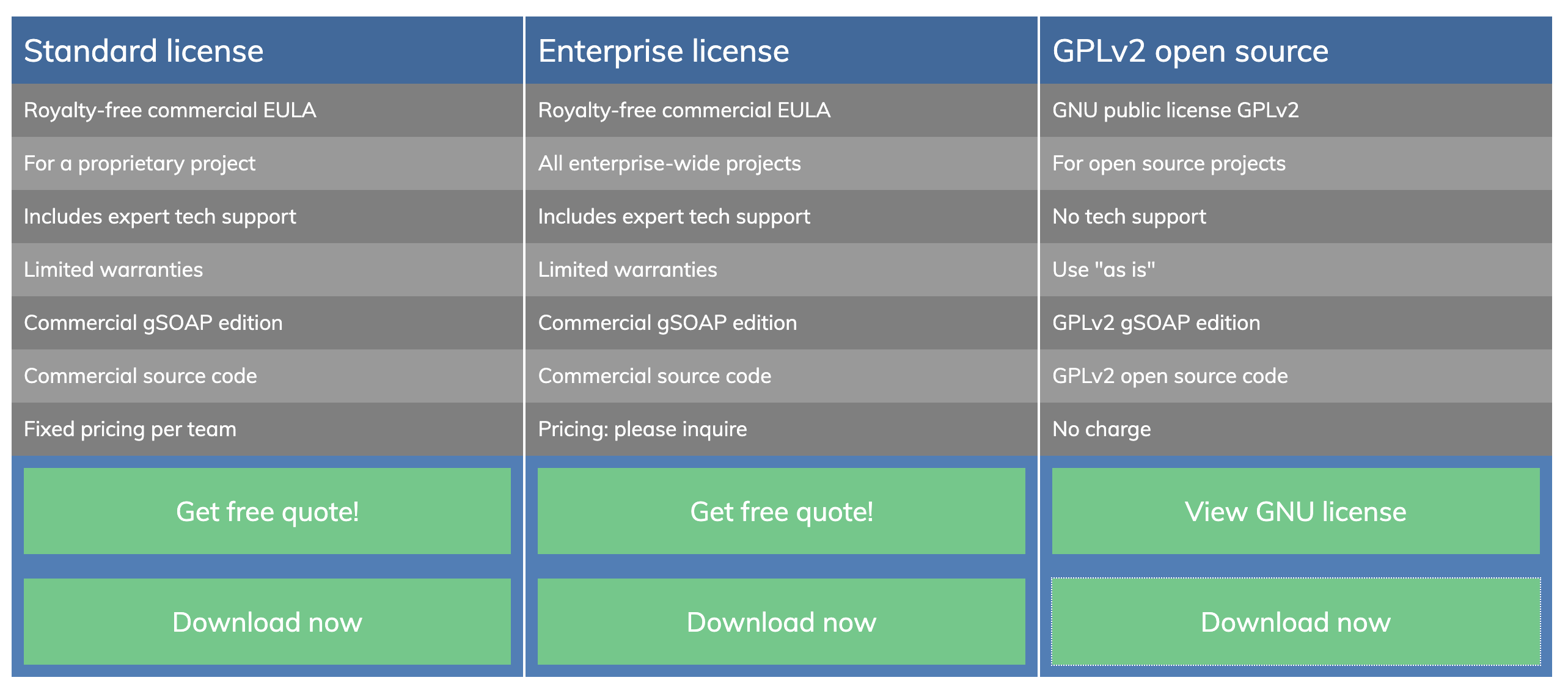
gsoap实现webservice服务
gsoap实现webservice服务 在实现Web服务时,使用gSOAP是一个很好的选择,因为它提供了强大的工具和库来创建SOAP和RESTful服务。gSOAP是一个C和C语言开发的库,它支持SOAP协议的各种版本,包括SOAP 1.1和SOAP 1.2。下面是如何使用gSO…...

容联云联络中心AICC:深度整合DeepSeek,业务验证结果公开
容联云重磅推出AICC3.2版本,实现了智能化的升级与外呼效率的突破——深度整合DeepSeek-R1大模型、预测式外呼在数据分析侧的增强、全渠道路由能力、一键多呼效率的强化。 同时,全面接入DeepSeek-R1的容联云 AICC3.2 ,目前已与某知名汽车金融企…...

腿足机器人之七- 逆运动学
腿足机器人之七- 逆运动学 基本概念腿部运动的数学表示坐标系定义以及自由度说明正运动学模型 逆运动学求解几何解法数值迭代法雅可比矩阵法基础双足机器人步态规划中的雅可比法应用 工程挑战与解决方案实际应用中的工具和算法多解问题高自由度机器人(如Atlas的28自…...

快速点位排查问题的方法
一、核心思路:缩小问题范围 1. 分治法(Divide and Conquer) 原理:将复杂系统拆分为独立模块,逐层验证。示例: 网络问题:检查客户端 → 本地网络 → 服务器 → 数据库。代码问题:注…...

【前端】Vue组件库之Element: 一个现代化的 UI 组件库
文章目录 前言一、官网1、官网主页2、设计原则3、导航4、组件 二、核心功能:开箱即用的组件生态1、丰富的组件体系2、特色功能亮点 三、快速上手:三步开启组件化开发1、安装(使用Vue 3)2、全局引入3、按需导入(推荐&am…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
