算法——结合实例了解Minimax算法(极小化极大算法)
计算机科学中最有趣的事情之一就是编写一个人机博弈的程序。有大量的例子,最出名的是编写一个国际象棋的博弈机器。但不管是什么游戏,程序趋向于遵循一个被称为Minimax算法,伴随着各种各样的子算法在一块。本篇将简要介绍 minimax 算法,并通过实例分析帮助大家更好的理解。
一、概念
Minimax算法又名极小化极大算法,是一种找出失败的最大可能性中的最小值的算法。Minimax算法常用于棋类等由两方较量的游戏和程序,这类程序由两个游戏者轮流,每次执行一个步骤。我们众所周知的五子棋、象棋等都属于这类程序,所以说Minimax算法是基于搜索的博弈算法的基础。该算法是一种零总和算法,即一方要在可选的选项中选择将其优势最大化的选择,而另一方则选择令对手优势最小化的方法。
(1)Minimax是一种悲观算法,即假设对手每一步都会将我方引入从当前看理论上价值最小的格局方向,即对手具有完美决策能力。因此我方的策略应该是选择那些对方所能达到的让我方最差情况中最好的,也就是让对方在完美决策下所对我造成的损失最小。
(2)Minimax不找理论最优解,因为理论最优解往往依赖于对手是否足够愚蠢,Minimax中我方完全掌握主动,如果对方每一步决策都是完美的,则我方可以达到预计的最小损失格局,如果对方没有走出完美决策,则我方可能达到比预计的最悲观情况更好的结局。总之我方就是要在最坏情况中选择最好的。
二、实例分析
实例一、井字棋中的应用
- 游戏规则和局面评估:井字棋是在 3×3 的棋盘上进行的游戏,玩家轮流在空格中放置自己的棋子(假设一方为 X,另一方为 O),率先将自己的三个棋子连成一线(横、竖或斜)的玩家获胜。如果棋盘填满后仍未出现连成一线的情况,则为平局。我们可以为每个局面定义一个评估值:如果 X 获胜,评估值为 + 1;如果 O 获胜,评估值为 - 1;如果是平局,评估值为 0。
- 构建游戏树:以 X 玩家为先手开始构建游戏树。在根节点处,X 玩家有 9 种可能的落子位置,每个位置对应一个子节点。对于每个子节点,O 玩家又有 8 种可能的落子位置,依此类推,直到游戏结束(出现获胜局面或平局)。
- Minimax 算法执行过程
- 叶节点评估:当到达游戏结束的局面(叶节点)时,根据游戏结果赋予评估值,如 X 获胜则评估值为 + 1,O 获胜则为 - 1,平局为 0。
- 回溯计算:从叶节点开始回溯,假设当前轮到 X 玩家(Max 玩家)决策,在其所处的节点,它会选择子节点中评估值最大的那个作为自己的最优策略。若当前轮到 O 玩家(Min 玩家)决策,它会选择子节点中评估值最小的那个。比如,在某个中间节点,X 玩家的三个子节点评估值分别为 - 1、0、1,那么 X 玩家会选择评估值为 1 的子节点对应的走法。
| |
---|---|---| |
---|---|---| | 假设当前棋盘为空,X 玩家考虑第一步的走法。算法会模拟所有可能的后续情况:
- X 选择左上角:然后 O 可能有多种回应,假设 O 选择中心位置。接着 X 再走,可能形成不同局面,继续模拟下去直到游戏结束,得到一个评估值。
- X 选择其他位置:同样依次模拟后续 O 的走法和 X 的应对,直到得出所有以 X 第一步不同走法为根节点的子树的评估值。假设经过计算,X 选择左上角后最终的评估值最高,那么算法就会认为 X 的第一步最优走法是左上角。
局限性和改进方向
- 局限性:Minimax 算法的时间复杂度和空间复杂度较高,随着游戏树的深度和广度增加,计算量呈指数级增长。在复杂的游戏中,如国际象棋、围棋等,可能无法在合理时间内计算出所有可能。
- 改进方向:为了减少计算量,可以采用 α-β 剪枝技术,在搜索过程中剪掉一些不可能影响最终结果的分支。还可以结合启发式函数,对局面进行更快速的评估,减少不必要的搜索深度。
实例二、纸币面值最大化最小
题目:现在考虑这样一个游戏:有三个盘子A、B和C,每个盘子分别放有三张纸币。A放的是1、20、50;B放的是5、10、100;C放的是1、5、20。单位均为“元”。有甲、乙两人,两人均对三个盘子和上面放置的纸币有可以任意查看。
游戏分三步:
(1)甲从三个盘子中选取一个。
(2)乙从甲选取的盘子中拿出两张纸币交给甲。
(3)甲从乙所给的两张纸币中选取一张,拿走。
其中甲的目标是最后拿到的纸币面值尽量大,乙的目标是让甲最后拿到的纸币面值尽量小。
基本思路:一般解决博弈类问题的自然想法是将格局组织成一棵树,树的每一个节点表示一种格局,而父子关系表示由父格局经过一步可以到达子格局。Minimax也不例外,它通过对以当前格局为根的格局树搜索来确定下一步的选择。而一切格局树搜索算法的核心都是对每个格局价值的评价。
解题:下图是上述示例问题的格局树:

注意,由于示例问题格局数非常少,我们可以给出完整的格局树。这种情况下我可以找到Minimax算法的全局最优解。而真实情况中,格局树非常庞大,即使是计算机也不可能给出完整的树,因此我们往往只搜索一定深度,这时只能找到局部最优解。
我们从甲的角度考虑。其中正方形节点表示轮到我方(甲),而三角形表示轮到对方(乙)。经过三轮对弈后(我方-对方-我方),将进入终局。黄色叶结点表示所有可能的结局。从甲方看,由于最终的收益可以通过纸币的面值评价,我们自然可以用结局中甲方拿到的纸币面值表示终格局的价值。
下面考虑倒数第二层节点,在这些节点上,轮到我方选择,所以我们应该引入可选择的最大价值格局,因此每个节点的价值为其子节点的最大值:

这些轮到我方的节点叫做max节点,max节点的值是其子节点最大值。
倒数第三层轮到对方选择,假设对方会尽力将局势引入让我方价值最小的格局,因此这些节点的价值取决于子节点的最小值。这些轮到对方的节点叫做min节点。
最后,根节点是max节点,因此价值取决于叶子节点的最大值。最终完整赋值的格局树如下:

总结一下Minimax算法的步骤:
(1)首先确定最大搜索深度D,D可能达到终局,也可能是一个中间格局。
(2)在最大深度为D的格局树叶子节点上,使用预定义的价值评价函数对叶子节点价值进行评价。
(3)自底向上为非叶子节点赋值。其中max节点取子节点最大值,min节点取子节点最小值。
(4)每次轮到我方时(此时必处在格局树的某个max节点),选择价值等于此max节点价值的那个子节点路径。
在上面的例子中,根节点的价值为20,表示如果对方每一步都完美决策,则我方按照上述算法可最终拿到20元,这是我方在Minimax算法下最好的决策。格局转换路径如下图红色路径所示:

注意几点:
(1)真实问题一般无法构造出完整的格局树,所以需要确定一个最大深度D,每次最多从当前格局向下计算D层。
(2)因为上述原因,Minimax一般是寻找一个局部最优解而不是全局最优解,搜索深度越大越可能找到更好的解,但计算耗时会呈指数级膨胀。
(3)也是因为无法一次构造出完整的格局树,所以真实问题中Minimax一般是边对弈边计算局部格局树,而不是只计算一次,但已计算的中间结果可以缓存。
三、伪代码
def minimax(node, depth, is_maximizing):if depth == 0 or node是终止节点:return 评估值if is_maximizing:value = -∞for child in node的子节点:value = max(value, minimax(child, depth-1, False))return valueelse:value = +∞for child in node的子节点:value = min(value, minimax(child, depth-1, True))return value
四、关键点
-
评估函数:需准确反映局面优劣(如棋子价值、位置优势)。
-
效率优化:实际应用中需结合剪枝(如Alpha-Beta剪枝)减少计算量。
-
深度限制:受计算资源限制,通常设置搜索深度。
总结
Minimax算法通过模拟对手最优策略,为当前玩家提供最稳健的决策。其核心是交替最小化与最大化收益,确保在最坏情况下争取最好结果。虽然理论完备,但实际应用需结合启发式评估和优化策略以提高效率。
相关文章:

算法——结合实例了解Minimax算法(极小化极大算法)
计算机科学中最有趣的事情之一就是编写一个人机博弈的程序。有大量的例子,最出名的是编写一个国际象棋的博弈机器。但不管是什么游戏,程序趋向于遵循一个被称为Minimax算法,伴随着各种各样的子算法在一块。本篇将简要介绍 minimax 算法&#…...

使用 DeepSeek 生成商城流程图
步骤 1.下载 mermaid 2.使用 DeepSeek 生成 mermaid 格式 3.复制内容到 4.保存备用。 结束。...

什么是GraphQL?
如果你在寻找漏洞利用方式,请参考下面的文章 GraphQL API 漏洞 |网络安全学院 GitHub - swisskyrepo/PayloadsAllTheThings: A list of useful payloads and bypass for Web Application Security and Pentest/CTF GraphQL 查询(Query) GraphQL 既不是…...

Spring Boot 的约定优于配置,你的理解是什么?
Spring Boot 的“约定优于配置”:开发效率的革命性提升 在软件开发中,开发者常常需要花费大量时间编写繁琐的配置文件,尤其是在传统的 Java EE 或 Spring 框架中。而 Spring Boot 通过“约定优于配置”(Convention Over Configur…...

C#开源大型商城系统之B2B2C+O2O一体化_OctShop
一、应用背景与引言 在当今数字化商业的浪潮中,电子商务平台的构建成为众多企业拓展业务、提升竞争力的关键举措。C# 语言以其强大的功能、高效的性能以及良好的开发框架支持,在商城系统开发领域占据着重要地位。独立开源的大型 C# 商城系统,…...

gitte远程仓库修改后,本地没有更新,本地与远程仓库不一致
问题 :gitte远程仓库修改后,本地没有更新,本地与远程仓库不一致 现象: [cxqiZwz9fjj2ssnshikw14avaZ rpc]$ git push Username for https://gitee.com: beihangya Password for https://beihangyagitee.com: To https://gitee.c…...

【对比】Pandas 和 Polars 的区别
Pandas vs Polars 对比表 特性PandasPolars开发语言Python(Cython 实现核心部分)Rust(高性能系统编程语言)性能较慢,尤其在大数据集上(内存占用高,计算效率低)极快,利用…...

el-input无法输入0.0001的小数,自动转换为0在vue3中的bug
今天遇到个bug,el-input中只能输入0.1或者输入0.1再加上00成为0.001,不能直接输入0.001,否则自动转换为0。需要去掉 v-model.number后面的 .number 源代码: <el-table-column label"实发数量" width"120"…...

Ubuntu 下 systemd 介绍
系列文章目录 Linux内核学习 Linux 知识(1) Linux 知识(2) WSL Ubuntu QEMU 虚拟机 Linux 调试视频 PCIe 与 USB 的补充知识 vscode 使用说明 树莓派 4B 指南 设备驱动畅想 Linux内核子系统 Linux 文件系统挂载 QEMU 通过网络实现…...
畅用七个模型架构)
BERT文本分类(PyTorch和Transformers)畅用七个模型架构
(PyTorch)BERT文本分类:七种模型架构 🌟 1. 介绍 使用BERT完成文本分类任务(如情感分析,新闻文本分类等等)对于NLPer已经是很基础的工作了!虽说已迈入LLM时代,但是BERT…...

两步在 Vite 中配置 Tailwindcss
第一步:安装依赖 npm i -D tailwindcss tailwindcss/vite第二步:引入 tailwindcss 更改配置 // src/main.js import tailwindcss/index// vite.config.js import vue from vitejs/plugin-vue import tailwindcss from tailwindcss/viteexport default …...

【vmware虚拟机安装教程】
以下是在VMware Workstation Pro上安装虚拟机的详细教程: 准备工作 下载VMware Workstation Pro 访问VMware官网下载并安装VMware Workstation Pro(支持Windows和Linux系统)。安装完成后,确保已激活软件(试用版或正式…...

文字转语音(三)FreeTTS实现
项目中有相关的功能,就简单研究了一下。 说明 FreeTTS 是一个基于 Java 的开源文本转语音(TTS)引擎,旨在将文字内容转换为自然语音输出。 FreeTTS 适合对 英文语音质量要求低、预算有限且需要离线运行 的场景,但若需…...

string类详解(上)
文章目录 目录1. STL简介1.1 什么是STL1.2 STL的版本1.3 STL的六大组件 2. 为什么学习string类3. 标准库中的string类3.1 string类3.2 string类的常用接口说明 目录 STL简介为什么学习string类标准库中的string类string类的模拟实现现代版写法的String类写时拷贝 1. STL简介 …...

Visual Studio Code使用ai大模型编成
1、在Visual Studio Code搜索安装roo code 2、去https://openrouter.ai/settings/keys官网申请个免费的配置使用...

外贸跨境订货系统流程设计、功能列表及源码输出
在全球化的商业环境下,外贸跨境订货系统对于企业拓展国际市场、提升运营效率至关重要。该系统旨在为外贸企业提供一个便捷、高效、安全的订货平台,实现商品展示、订单管理、物流跟踪等功能,满足跨境业务的多样化需求。以下将详细阐述外贸订货…...

TraeAi上手体验
一、Trae介绍 由于MarsCode 在国内由于规定限制,无法使用 Claude 3.5 Sonnet 模型,字节跳动选择在海外推出 Trae,官网:https://www.trae.ai/。 二、安装 1.下载安装Trae-Setup-x64.exe 2.注册登录 安装完成后,点击登…...

深入解析 vLLM:高性能 LLM 服务框架的架构之美(一)原理与解析
修改内容时间2.4.1处理请求的流程,引用更好的流程图2025.02.11首发2025.02.08 深入解析 vLLM:高性能 LLM 服务框架的架构之美(一)原理与解析 深入解析 vLLM:高性能 LLM 服务框架的架构之美(二)…...

thingboard告警信息格式美化
原始报警json内容: { "severity": "CRITICAL","acknowledged": false,"cleared": false,"assigneeId": null,"startTs": 1739801102349,"endTs": 1739801102349,"ackTs": 0,&quo…...

redis解决高并发看门狗策略
当一个业务执行时间超过自己设定的锁释放时间,那么会导致有其他线程进入,从而抢到同一个票,所有需要使用看门狗策略,其实就是开一个守护线程,让守护线程去监控key,如果到时间了还未结束,就会将这个key重新s…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
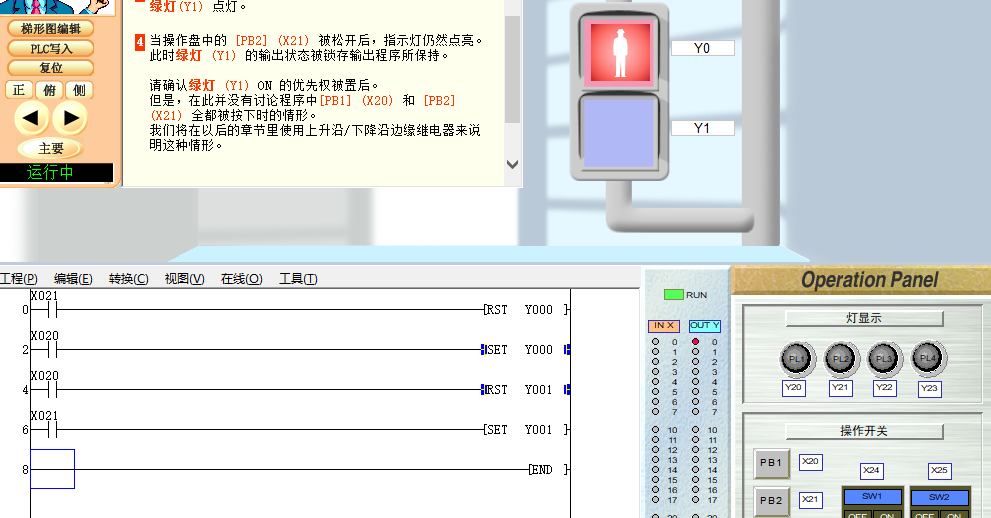
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...
