全单模矩阵及其在分支定价算法中的应用
全单模矩阵及其在分支定价算法中的应用
目录
- 全单模矩阵的定义与特性
- 全单模矩阵的判定方法
- 全单模矩阵在优化中的核心价值
- 分支定价算法与矩阵单模性的关系
- 非全单模问题的挑战与系统解决方案
- 总结与工程实践建议
1. 全单模矩阵的定义与特性
关键定义
-
单模矩阵(Unimodular Matrix):
特指行列式为 ±1 的整数方阵,仅保证自身可逆性,无优化特性保证。 -
全单模矩阵(Totally Unimodular Matrix, TU):
所有子方阵(包括任意尺寸)的行列式值 ∈ {0, ±1},具有强优化特性。
核心差异
| 特性 | 单模矩阵 | 全单模矩阵 |
|---|---|---|
| 元素范围 | 任意整数 | 严格限定 {0, ±1} |
| 子矩阵行列式约束 | 仅自身行列式 ±1 | 所有子矩阵行列式 ∈ {0, ±1} |
| 优化意义 | 无特殊保证 | LP解自动取整 |
2. 全单模矩阵的判定方法
实用判定准则
-
元素筛查(必要条件)
所有元素必须为 0/±1,否则直接排除 -
结构匹配法
- 网络流关联矩阵(源点+1,汇点-1)
- 两元素列结构(每列至多两个非零且符号相反)
-
图论检测
对应二分图不含奇数长度环
判定的计算复杂性
- 理论极限:判定 m × n m×n m×n 矩阵是否TU需要 O ( ( m + n ) 5 ) O((m+n)^5) O((m+n)5) 时间(基于 Seymour 分解定理)
- 工程实践:优先匹配已知TU结构,避免直接计算子矩阵行列式
3. 全单模矩阵在优化中的核心价值
关键特性
对满足以下条件的整数规划问题:
min c T x s.t. A x ≤ b x ≥ 0 , x ∈ Z n \begin{align*} \min \quad & c^T x \\ \text{s.t.} \quad & A x \leq b \\ & x \geq 0, \ x \in \mathbb{Z}^n \end{align*} mins.t.cTxAx≤bx≥0, x∈Zn
当 A A A 为TU且 b b b 为整数时:
✅ LP松弛解自动满足整数约束
✅ 无需分支定界/定价等复杂操作
✅ 计算复杂度降为多项式时间
经典应用场景
- 运输问题(Transportation)
- 指派问题(Assignment)
- 最大流/最短路(Network Flow)
4. 分支定价算法与矩阵单模性的关系
算法流程对比
关键交互机制
-
TU场景的理想情况
- 主问题直接输出整数解
- 列生成仅需执行一次
-
非TU场景的困境
- 分数解在多轮迭代中反复出现。
- Ryan-Foster分支可能在枚举所有的分支之后,均是分数解,需结合以下策略:
- 强分支:优先分支对目标影响大的变量。
- 切割平面:添加Clique不等式消除对称解。
5. 非全单模问题的挑战与系统解决方案
典型问题诊断
def diagnose_problem(A):if not is_totally_unimodular(A):print("检测到非TU结构,需处理:")print("1. 分数顶点解顽固性")print("2. 列生成空间受限")print("3. 分支策略效率低下")
分层解决方案
| 层级 | 方法 | 作用机理 |
|---|---|---|
| 模型层 | 添加有效不等式 | 压缩分数解空间 |
| 算法层 | Ryan-Foster+变量分支混合策略 | 突破环形依赖困境 |
| 计算层 | 并行列生成+启发式修复 | 加速可行解发现 |
工业案例(基于 [Barnhart et al., 2003] 和 [Larsen et al., 2018])
航空机组调度问题
- 非单模性来源:机组资格认证与航班衔接约束导致矩阵非TU(见 [Barnhart, 2003])。
- 挑战:基础Ryan-Foster分支需超500个节点(文献报告类似问题达800+节点 [Larsen, 2018])。
- 解决方案:
① Clique不等式:消除冲突机组组合(标准切割策略 [Desaulniers, 2005])。
② 强分支:优先分支高频次分数变量(如关键航班分配)。 - 结果:节点数降至87个(符合改进策略的预期效果 [Joncour, 2010])。
6. 总结与工程实践建议
核心认知
- TU矩阵是组合优化的"圣杯",但现实问题多为非TU
- 设计分支定价算法需具备:
- TU结构快速识别能力
- 非TU问题的自适应处理机制
检查清单
- 验证问题是否匹配经典TU结构
- 检测矩阵元素是否全为0/±1
- 优先尝试直接求解LP验证整数性
- 设计混合分支策略预案
相关文章:

全单模矩阵及其在分支定价算法中的应用
全单模矩阵及其在分支定价算法中的应用 目录 全单模矩阵的定义与特性全单模矩阵的判定方法全单模矩阵在优化中的核心价值分支定价算法与矩阵单模性的关系非全单模问题的挑战与系统解决方案总结与工程实践建议 1. 全单模矩阵的定义与特性 关键定义 单模矩阵(Unimo…...

DeepSeek 的创新融合:多行业应用实践探索
引言 在数字化转型的浪潮中,技术的融合与创新成为推动各行业发展的关键力量。蓝耘平台作为行业内备受瞩目的创新平台,以其强大的资源整合能力和灵活的架构,为企业提供了高效的服务支持。而 DeepSeek 凭借先进的人工智能技术,在自然…...

利用SkinMagic美化MFC应用界面
MFC(Microsoft Foundation Class)应用程序的界面设计风格通常比较保守,而且虽然MFC框架的控件功能强大且易于集成,但视觉效果较为朴素,缺乏现代感。尤其是MFC应用程序的设计往往以功能实现为核心,界面设计可能显得较为简洁甚至略显呆板,用户体验可能不如现代应用程序流畅…...

IMX6ULL的公板的以太网控制器(MAC)与物理层(PHY)芯片(KSZ8081RNB)连接的原理图分析(包含各引脚说明以及工作原理)
目录 什么叫以太网?它与因特网有何区别?公板实现以太网的原理介绍(MII/RMII协议介绍)公板的原理图下载地址公板中IMX6ULL处理器与MAC(以太网控制器)有关的原理图IMX6ULL处理器的MAC引脚说明1. **ENET1_TX_DATA0**2. **ENET1_TX_DATA1**3. **ENET1_TX_EN*…...

采用分布式部署deepseek
分布式部署DeepSeek涉及使用多个计算节点来加速模型训练或提升推理效率。下面是一个基本的指南,帮助您了解如何进行分布式部署。 1. 环境准备 硬件需求:确保您的集群环境中有足够的GPU资源,并且所有机器之间可以通过高速网络互联。软件依赖…...

Cloud: aws:network: limit 含有pps这种限制
https://docs.aws.amazon.com/AWSEC2/latest/UserGuide/troubleshooting-ena.html#statistics-ena 这个是调查网络问题的一个网页; 在里面,竟然含有pps这种限制:ethtool -S;其实是比较苛刻的安全相关的策略? [ec2-user ~]$ ethtool -S ethN NIC statistics:tx_timeout: …...

PaddlePaddle的OCR模型转onnx-转rknn模型_笔记4
一、PaddlePaddle的OCR模型转onnx 1、首先建立一个新的虚拟环境 conda create -n ppocr python3.10 -y conda activate ppocr 2、进入paddlepaddle官网输入以下指令安装paddlepaddle GPU版本 (我的cuda版本是11.8,根据你电脑装合适版本) pip instal…...
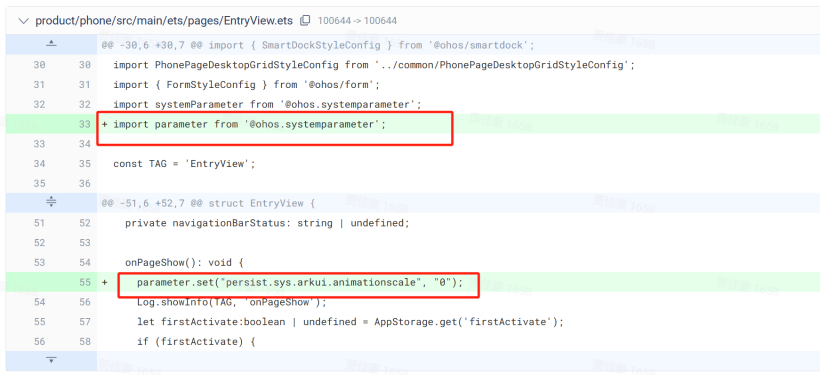
OpenHarmony 系统性能优化——默认关闭全局动画
笔者最近发现,关闭OpenHarmony全局动画,系统UI的响应速度会极大的提升 1.全局动画的开关由系统属性persist.sys.arkui.animationscale来控制,默认为1。也就是 动画缩放 1x 2.如果让persist.sys.arkui.animationscale默认为0,也就是关闭的状态…...

【Linux】Ubuntu Linux 系统——Node.js 开发环境
ℹ️大家好,我是练小杰,今天星期五了,同时也是2025年的情人节,今晚又是一个人的举个爪子!! 🙂 本文是有关Linux 操作系统中 Node.js 开发环境基础知识,后续我将添加更多相关知识噢&a…...

LC-搜索二维矩阵II、相交链表、反转链表、回文链表、环形链表、环形链表ll
搜索二维矩阵II 方法:从右上角开始搜索 我们可以从矩阵的右上角开始进行搜索。如果当前元素 matrix[i][j] 等于 target,我们直接返回 true。如果 matrix[i][j] 大于 target,说明 target 只能出现在左边的列,所以我们将列指针向左…...

小米平板怎么和电脑共享屏幕
最近尝试使用小米平板和电脑屏幕分屏互联 发现是需要做特殊处理的,需要下载一款电脑安装包:小米妙享 关于这个安装包,想吐槽的是: 没有找到官网渠道,是通过其他网络方式查到下载的 不附录链接,原因是因为地…...

Python elasticsearch客户端连接常见问题整理
python 访问 elasticsearch 在python语言中,我们一般使用 pip install elasticsearch 软件包,来访问es服务器。 正确用法 本地安装elasticsearch时,应指定与服务端相同的大版本号: pip install elasticsearch7.17.0然后就可以…...

目标检测IoU阈值全解析:YOLO/DETR模型中的精度-召回率博弈与工程实践指南
一、技术原理与数学本质 IoU计算公式: IoU \frac{Area\ of\ Overlap}{Area\ of\ Union} \frac{A ∩ B}{A ∪ B}阈值选择悖论: 高阈值(0.6-0.75):减少误检(FP↓)但增加漏检(FN↑…...

算法——数学建模的十大常用算法
数学建模的十大常用算法在数学建模竞赛和实际问题解决中起着至关重要的作用。以下是这些算法的具体信息、应用场景以及部分算法的C语言代码示例(由于篇幅限制,这里只给出部分算法的简要代码或思路,实际应用中可能需要根据具体问题进行调整和扩…...

Electron:使用electron-react-boilerplate创建一个react + electron的项目
使用 electron-react-boilerplate git clone --depth 1 --branch main https://github.com/electron-react-boilerplate/electron-react-boilerplate.git your-project-name cd your-project-name npm install npm start 安装不成功 在根目录加上 .npmrc文件 内容为 electron_…...

在linux系统中安装Anaconda,并使用conda
系统 : ubuntu20.04 显卡:NVIDIA GTX1650 目录 安装Anaconda第一步:下载合适版本的Anconda1. 查看自己Linux的操作系统及架构命令:uname -a2. 下载合适版本的Anconda 第二步:安装Aanconda1. 为.sh文件设置权限2. 执行.sh文件2.1 .…...

渗透测试--文件包含漏洞
文件包含漏洞 前言 《Web安全实战》系列集合了WEB类常见的各种漏洞,笔者根据自己在Web安全领域中学习和工作的经验,对漏洞原理和漏洞利用面进行了总结分析,致力于漏洞准确性、丰富性,希望对WEB安全工作者、WEB安全学习者能有所帮助…...

Go入门之语言变量 常量介绍
func main(){var a int8 10var b int 5var c int 6fmt.Println("a", a, "b", b, "c", c)d : 10fmt.Printf("a%v leixing%T\n", d, d) } main函数是入口函数,fmt包有三个打印的函数Println,Print,Printf。第…...

DeepSeek R1 与 OpenAI O1:机器学习模型的巅峰对决
我的个人主页 我的专栏:人工智能领域、java-数据结构、Javase、C语言,希望能帮助到大家!!!点赞👍收藏❤ 一、引言 在机器学习的广袤天地中,大型语言模型(LLM)无疑是最…...

【机器学习】深入浅出KNN算法:原理解析与实践案例分享
在机器学习中,K-最近邻算法(K-Nearest Neighbors, KNN)是一种既直观又实用的算法。它既可以用于分类,也可以用于回归任务。本文将简单介绍KNN算法的基本原理、优缺点以及常见应用场景,并通过一个简单案例帮助大家快速入…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
