Git如何将一个分支的内容同步到另一个分支
在 Git 中,可以通过多种方法将一个分支的内容同步到另一个分支。以下是几种常用的方法:
1. 使用 merge 命令
这是最常见的方法,将一个分支的更改合并到另一个分支。
# 切换到目标分支
git checkout target-branch# 合并源分支的内容
git merge source-branch
2. 使用 rebase 命令
rebase 可以将一个分支的更改应用到另一个分支的基础之上,从而保持更清晰的提交历史。
# 切换到源分支
git checkout source-branch# 进行 rebase
git rebase target-branch# 切换回目标分支
git checkout target-branch# 合并变基后的源分支
git merge source-branch
3. 使用 cherry-pick 命令
如果只想将源分支中的特定提交应用到目标分支,可以使用 cherry-pick。
# 切换到目标分支
git checkout target-branch# 应用特定的提交
git cherry-pick <commit-hash>
4. 使用 reset 命令(谨慎使用)
如果目标分支的当前状态不需要保留,可以使用 reset 来强制将其重置为源分支的状态。
# 切换到目标分支
git checkout target-branch# 强制重置
git reset --hard source-branch
5. 同步远程分支
如果需要将更改推送到远程分支,可以在合并或 rebase 后使用:
git push origin target-branch
相关文章:

Git如何将一个分支的内容同步到另一个分支
在 Git 中,可以通过多种方法将一个分支的内容同步到另一个分支。以下是几种常用的方法: 1. 使用 merge 命令 这是最常见的方法,将一个分支的更改合并到另一个分支。 # 切换到目标分支 git checkout target-branch# 合并源分支的内容 git m…...

[C#]C# winform部署yolov12目标检测的onnx模型
yolov12官方框架:github.com/sunsmarterjie/yolov12 【测试环境】 vs2019 netframework4.7.2 opencvsharp4.8.0 onnxruntime1.16.3 【效果展示】 【调用代码】 using System; using System.Collections.Generic; using System.ComponentModel; using System.…...

51c大模型~合集69
我自己的原文哦~ https://blog.51cto.com/whaosoft/12221979 #7项基于SAM万物分割模型研究工作 1、CC-SAM: SAM with Cross-feature Attention and Context for Ultrasound Image Segmentation #ECCV2024 #SAM #图像分割 #医学图像 Segment Anything Model (SAM) 在自…...

2025寒假周报4
2025寒假天梯训练7-CSDN博客 眨眼间寒假训练就告一段落了,准备回校继续战斗了。这周练了3场OI赛制的篮球杯,感觉非常糟糕,不像天梯赛,天梯赛打起来非常舒适顺畅,一直都不喜欢OI赛制,打着非常不稳定..还需要…...

自学Java-AI结合GUI开发一个石头迷阵的游戏
自学Java-AI结合GUI开发一个石头迷阵的游戏 准备环节1、创建石头迷阵的界面2、打乱顺序3、控制上下左右移动4、判断是否通关5、统计移动步骤,重启游戏6、拓展问题 准备环节 技术: 1、GUI界面编程 2、二维数组 3、程序流程控制 4、面向对象编程 ∙ \bulle…...

buuctf-[极客大挑战 2019]Knife题解
一个很简单的web题,进入界面 网页名还加白给的shell,并且给的提示也很明显,给了一个一句话木马再加上菜刀,很怀疑是一个webshell题,那么直接打开蚁剑测试连接拿shell 用提示的一句话木马的密码,测试链接发现…...

Spring MVC 对象转换器:初级开发者入门指南
Spring MVC 对象转换器:初级开发者入门指南 为什么需要对象转换器? 在 Web 应用中,我们经常需要处理不同类型的对象。例如:前端数据到后端对象 :用户通过表单提交的数据通常是HttpServletRequest 对象,我们…...

语音直播交友app出海:语音直播交友系统软件源码搭建国际化发展技术层面分析
随着移动互联网的普及和全球社交需求的增长以及国内如火如荼的Ai大模型引起的全球发展热潮,语音直播软件出海成为了具有巨大发展潜力的业务领域。以下是一些关键的技术方向,将为语音直播软件在国际市场的成功推广及搭建合作奠定基础。 通信技术 实时语音…...
Web Scraper,强大的浏览器爬虫插件!
Web Scraper是一款功能丰富的浏览器扩展爬虫工具,有着直观的图形界面,无需编写代码即可自定义数据抓取规则,高效地从网页中提取结构化数据,而且它支持灵活的数据导出选项,广泛应用于电商监控、内容聚合、市场调研等多元…...

EasyRTC:基于WebRTC与P2P技术,开启智能硬件音视频交互的全新时代
在数字化浪潮的席卷下,智能硬件已成为我们日常生活的重要组成部分,从智能家居到智能穿戴,从工业物联网到远程协作,设备间的互联互通已成为不可或缺的趋势。然而,高效、低延迟且稳定的音视频交互一直是智能硬件领域亟待…...

go 定时任务 gocron timer
选型推荐(DeepSeek) 简单任务调度: 推荐使用 cron 或 gocron,它们轻量且易用。 复杂任务调度: 推荐使用 go-quartz,支持任务依赖和持久化。 分布式任务调度: 推荐使用 asynq,基于 Redis 实现,适合分布式…...

uniapp引入uview组件库(可以引用多个组件)
第一步安装 npm install uview-ui2.0.31 第二步更新uview npm update uview-ui 第三步在main.js中引入uview组件库 第四步在uni.scss中引入import "uview-ui/theme.scss"样式 第五步在文件中使用组件...

MySQL主从架构
MySQL主从架构 MySQL REPLICATION 在实际生产环境中,如果对数据库的读和写都在一个数据库服务器中操作。无论是在安全性、高可用性,还是高并发等各个方面都是完全不能满足实际需求的,因此,一般来说都是通过主从复制(…...

科普mfc100.dll丢失怎么办?有没有简单的方法修复mfc100.dll文件
当电脑频繁弹窗提示“mfc100.dll丢失”或应用程序突然闪退时,这个看似普通的系统文件已成为影响用户体验的核心痛点。作为微软基础类库(MFC)的核心组件,mfc100.dll直接关联着Visual Studio 2010开发的大量软件运行命脉。从工业设计…...
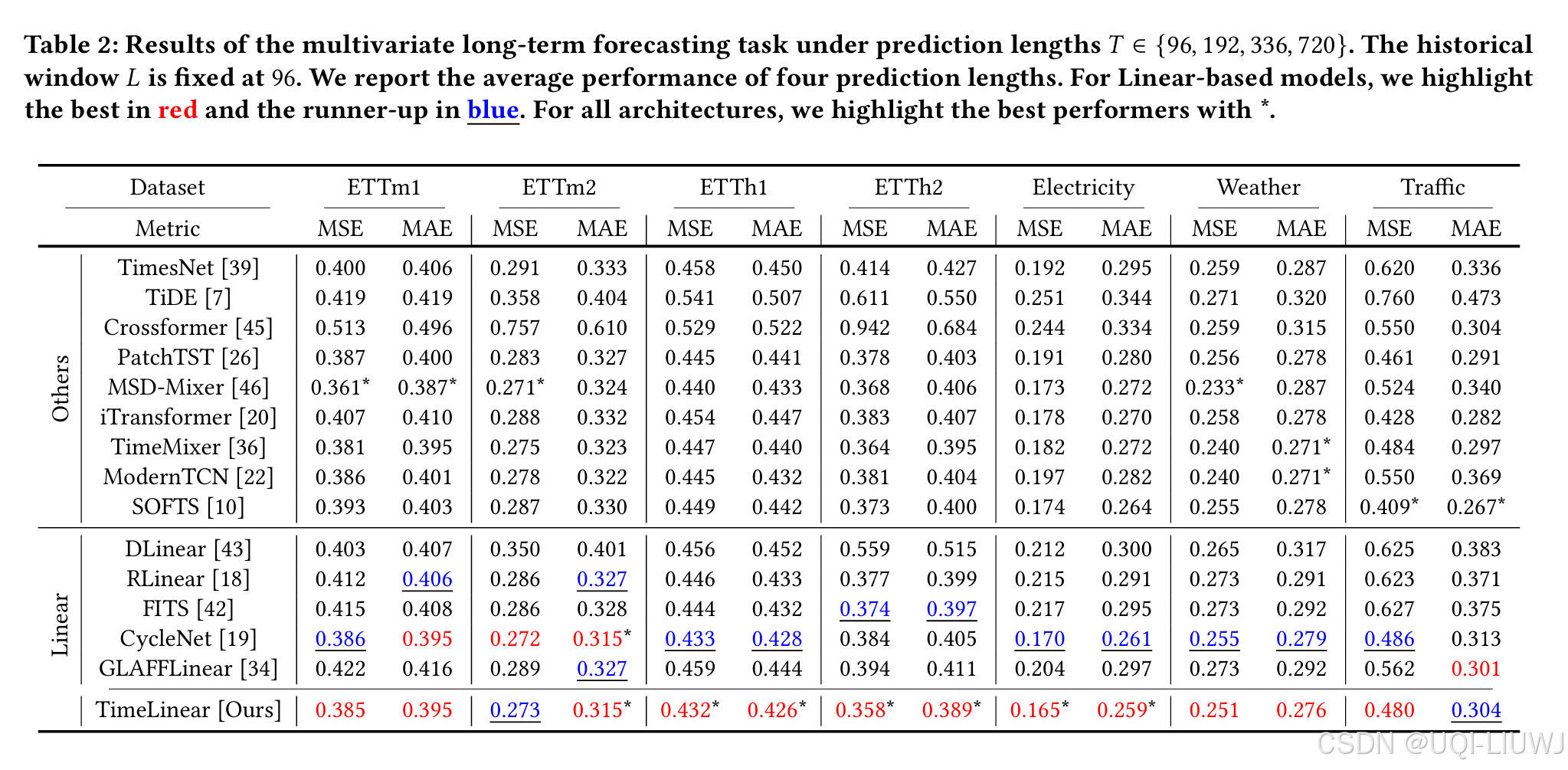
论文笔记:How Much Can Time-related Features Enhance Time Series Forecasting?
202412arxiv 许多时间序列预测方法靠变量建模,却忽略了时间戳相关特征(如季节、月份、星期几、小时、分钟等) ——>论文尝试仅基于时间戳进行预测(这个仅我觉得其实不是很严谨,还是用了时间序列变量的数据【不可能…...

Qt学习(六) 软件启动界面 ,注册表使用 ,QT绘图, 视图和窗口绘图,Graphics View绘图框架:简易CAD
一 软件启动界面 注册表使用 知识点1:这样创建的界面是不可以拖动的,需要手动创建函数来进行拖动,以下的3个函数是从父类继承过来的函数 virtual void mousePressEvent(QMouseEvent *event);virtual void mouseReleaseEvent(QMouseEvent *eve…...
--WebAssembly 基础入门)
JavaScript系列(80)--WebAssembly 基础入门
WebAssembly 基础入门 🚀 WebAssembly(简称Wasm)是一种低级的类汇编语言,它具有紧凑的二进制格式,能够以接近原生的性能在现代Web浏览器中运行。让我们深入了解这项革命性的技术。 WebAssembly 概述 🌟 &…...

蓝桥杯刷题2.21|笔记
参考的是蓝桥云课十四天的那个题单,不知道我发这个有没有问题,如果有问题找我我立马删文。(参考蓝桥云课里边的题单,跟着大佬走,应该是没错滴,加油加油) 一、握手问题 #include <iostream&g…...

053 性能压测 单机锁 setnx
文章目录 性能压测-压力测试索引thymeleafnginx减少数据库查询(代码有bug)缓存 安全单机锁(防止缓存击穿)setnx pom.xml 性能压测-压力测试 1 响应时间(Response Time: RT):响应时间指用户从客…...

【天线】IFA天线知识点摘抄
MIFA天线的尺寸与性能关系 1,辐射效率 天线越小,辐射效率越低。唯一好处是减少PCB占用空间 2,带宽 一般MIFA天线在2.4G频段内的带宽:S11≤-10dB的范围为2.44GHz230MHz。较小的尺寸可能会限制带宽 3,增益 MIFA天线的…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
