信息学奥赛一本通 1520:【 例 1】分离的路径 | 洛谷 P2860 [USACO06JAN]Redundant Paths G
【题目链接】
ybt 1520:【 例 1】分离的路径
洛谷 P2860 [USACO06JAN]Redundant Paths G
【题目考点】
1. 图论:割边(桥) 边双连通分量
【解题思路】
每个草场是一个顶点,草场之间的双向路是无向边,该图是无向图。建新的道路,就是添加边。
“每对草场之间已经有至少一条路径”,表示该图是连通图。
“同一对草场之间,可能已经有两条不同的道路”,表示图中可能有重边。
“使每一对草场之间都会至少有两条相互分离的路径”,而且“两条路径相互分离,是指两条路径没有一条重合的道路”,也就是希望最后图中任何两个顶点之间都有两条边不重复的路径,这样的图就是边双连通图。
求的是最少增加的路径的数目。
该题抽象后可以描述为:给定一个无向图,求最少添加几条边可以使该图变为边双连通图。
如果两顶点处于一个边双连通分量中,那么这两顶点之间就一定不需要添加边,因为两顶点之间已经存在两条边不重复的路径。因此只有两顶点在不同的边双连通分量中,才需要考虑是否需要在两顶点之间添加边。
这里可以考虑将图中每个边双连通分量变为一个顶点,也就是“缩点”,缩点后的图一定不存在双连通分量,是无环连通图,也就是树。
反证:如果缩点后存在环,那么环上多个顶点处于一个双连通分量中,在原图中该环连接的所有双连通分量应该同属于一个双连通分量,应该缩为一个点而不是多个点。
考虑要想使缩点后的树变为双连通图,需要添加最少多少条边。
树上任意两顶点连线后,就会形成一个环,该环就是一个双连通分量。
由于环上的顶点都是度为2的顶点,因此树上叶子结点,也就是度为1的顶点要想处于一个环上,必须在度为1的顶点上连接新的边,使该顶点度变为2。
因此每次添加一条边连接两个度为1的顶点,让这两个顶点在树上的路径加上新的边形成一个环。
每两个度为1的顶点需要添加一条边,如果剩下单独一个顶点,也需要在该顶点上增加一条到其它顶点的边。
如果叶子结点数量为 d d d,那么需要添加边的数量为 ⌈ d 2 ⌉ \lceil \frac{d}{2} \rceil ⌈2d⌉,也就是 d + 1 2 \frac{d+1}{2} 2d+1
【题解代码】
解法1:Tarjan算法直接求边双连通分量
#include <bits/stdc++.h>
using namespace std;
#define N 5005
int n, m, fa[N], ebc[N], en, deg[N];
vector<int> edge[N];
int dfn[N], low[N], ts;
stack<int> stk;
void tarjan(int u)
{int t, fromEdge = 0;//fromEdge:从fa[u]到u的边的数量 dfn[u] = low[u] = ++ts;stk.push(u);for(int v : edge[u]){if(dfn[v] == 0){fa[v] = u;tarjan(v);low[u] = min(low[u], low[v]);}else if(v != fa[u] || ++fromEdge > 1)//如果fromEdge==2,那么(u, fa[u])存在重边,更新low[u]后可以保证(u,fa[u])不是桥 low[u] = min(low[u], dfn[v]);}if(dfn[u] == low[u]){en++;do{t = stk.top();stk.pop();ebc[t] = en;}while(t != u);}
}
int main()
{int f, t, degOneCt = 0;cin >> n >> m;for(int i = 1; i <= m; ++i){cin >> f >> t;edge[f].push_back(t);edge[t].push_back(f);}for(int v = 1; v <= n; ++v) if(dfn[v] == 0)tarjan(v);for(int u = 1; u <= n; ++u)for(int v : edge[u]) if(ebc[v] != ebc[u])deg[ebc[v]]++, deg[ebc[u]]++;for(int i = 1; i <= en; ++i)//<u, v>, <v, u>统计两次,顶点的度应该除以2 deg[i] /= 2;for(int i = 1; i <= en; ++i) if(deg[i] == 1)//统计度为1的双连通分量的数量 degOneCt++;cout << (degOneCt+1)/2;return 0;
}
解法2:Tarjan算法先求桥,再求双连通分量
#include <bits/stdc++.h>
using namespace std;
#define N 5005
int n, m, fa[N], ebc[N], en, deg[N];
vector<int> edge[N];
int dfn[N], low[N], ts;
bool bridge[N], vis[N];//bridge[i]:(i, fa[i])是否是桥
bool isBridge(int u, int v)
{return fa[u] == v && bridge[u] || fa[v] == u && bridge[v];
}
void tarjan(int u)
{int t, fromEdge = 0;//fromEdge:从fa[u]到u的边的数量 dfn[u] = low[u] = ++ts;for(int v : edge[u]){if(dfn[v] == 0){fa[v] = u;tarjan(v);low[u] = min(low[u], low[v]);if(dfn[u] < low[v])bridge[v] = true;//(u,v)是桥 }else if(v != fa[u] || ++fromEdge > 1)//如果fromEdge==2,那么(u, fa[u])存在重边,更新low[u]后可以保证(u,fa[u])不是桥 low[u] = min(low[u], dfn[v]);}
}
void dfs(int u)
{vis[u] = true;ebc[u] = en;for(int v : edge[u]) if(!vis[v] && !isBridge(u, v))dfs(v);
}
int main()
{int f, t, degOneCt = 0;cin >> n >> m;for(int i = 1; i <= m; ++i){cin >> f >> t;edge[f].push_back(t);edge[t].push_back(f);}for(int v = 1; v <= n; ++v) if(dfn[v] == 0)tarjan(v);for(int v = 1; v <= n; ++v) if(!vis[v]){++en;dfs(v); }for(int u = 1; u <= n; ++u)for(int v : edge[u]) if(ebc[v] != ebc[u])deg[ebc[v]]++, deg[ebc[u]]++;for(int i = 1; i <= en; ++i)//<u, v>, <v, u>统计两次,顶点的度应该除以2 deg[i] /= 2;for(int i = 1; i <= en; ++i) if(deg[i] == 1)//统计度为1的双连通分量的数量 degOneCt++;cout << (degOneCt+1)/2;return 0;
}
相关文章:

信息学奥赛一本通 1520:【 例 1】分离的路径 | 洛谷 P2860 [USACO06JAN]Redundant Paths G
【题目链接】 ybt 1520:【 例 1】分离的路径 洛谷 P2860 [USACO06JAN]Redundant Paths G 【题目考点】 1. 图论:割边(桥) 边双连通分量 【解题思路】 每个草场是一个顶点,草场之间的双向路是无向边,该…...

架构师面试(六):熔断和降级
问题 在千万日活的电商系统中,商品列表页服务通过 RPC 调用广告服务;经过统计发现,在最近10秒的时间里,商品列表页服务在对广告服务的调用中有 98% 的调用是超时的; 针对这个场景,下面哪几项的说法是正确的…...

使用 DeepSeek 生成流程图、甘特图与思维导图:结合 Typora 和 XMind 的高效工作流
在现代工作与学习中,可视化工具如流程图、甘特图和思维导图能够极大地提升信息整理与表达的效率。本文将详细介绍如何使用 DeepSeek 生成 Mermaid 文本,结合 Typora 快速生成流程图和甘特图,并通过 Markdown 格式生成思维导图,最终…...

粘贴到Word里的图片显示不全
粘贴到Word里的图片显示不全,可从Word设置、图片本身、软件与系统等方面着手解决,具体方法如下: Word软件设置 经实践发现,图片在word行距的行距出现问题,可以按照如下调整行距进行处理 修改段落行距: 选…...

【C语言】结构体内存对齐问题
1.结构体内存对齐 我们已经基本掌握了结构体的使用了。那我们现在必须得知道结构体在内存中是如何存储的?内存是如何分配的?所以我们得知道如何计算结构体的大小?这就引出了我们今天所要探讨的内容:结构体内存对齐。 1.1 对齐规…...

【蓝桥杯单片机】第十三届省赛第二场
一、真题 二、模块构建 1.编写初始化函数(init.c) void Cls_Peripheral(void); 关闭led led对应的锁存器由Y4C控制关闭蜂鸣器和继电器 2.编写LED函数(led.c) void Led_Disp(unsigned char ucLed); 将ucLed取反的值赋给P0 开启锁存器 关闭锁存…...
)
类与对象(5)
上一章是类与对象(4)-CSDN博客 深入了构造函数和静态成员,大概讲解了类型转换 最后一章最后一章 友元 在 C 中,友元提供了一种突破类的访问控制(封装)的方式。通过友元,外部的函数或类可以访…...

AI知识架构之数据采集
数据采集 数据格式: 结构化数据:以固定格式和结构存储,如数据库中的表以及 Excel 表格,易于查询和分析。半结构化数据:有一定结构但不如结构化数据严格,XML 常用于数据交换,JSON 在 Web 应用中广泛用于数据传输和存储。非结构化数据:无预定义结构,文本、图像、音频和视…...

细说STM32F407单片机2个ADC使用DMA同步采集各自的1个输入通道的方法
目录 一、示例说明 二、工程配置 1、RCC、DEBUG、CodeGenerator 2、USART6 3、TIM3 (1)Mode (2)参数设置 (3) TRGO (4)ADC1_IN0 1)ADCs_Common_Settings 2&a…...
)
C# 将非托管Dll嵌入exe中(一种实现方法)
一、环境准备 电脑系统:Windows 10 专业版 20H2 IDE:Microsoft Visual Studio Professional 2022 (64 位) - Current 版本 17.11.4 其他: 二、测试目的 将基于C++创建DLL库,封装到C#生成的exe中。 一般C++创建的库,在C#中使用,都是采用DllImport导入的,且要求库处…...

完美解决:.vmx 配置文件是由 VMware 产品创建,但该产品与此版 VMware Workstation 不兼容
参考文章:该产品与此版 VMware Workstation 不兼容,因此无法使用 问题描述 当尝试使用 VMware Workstation 打开别人的虚拟机时,可能会遇到以下报错: 此问题常见于以下场景: 从其他 VMware 版本(如 ESX…...

使用大语言模型对接OA系统,实现会议室预定功能
随着人工智能技术的不断进步,越来越多的企业开始借助 AI 助手来提高工作效率,尤其是在日常事务的自动化处理中。比如,在许多公司里,会议室的预定是一个常见且频繁的需求,通常需要员工手动检查空闲时间并做出选择。而通…...

Ryu控制器:L2交换功能实现案例
基于 Ryu控制器 在 VM1--OVS--VM2 的简单拓扑中实现流量自动下发(流表动态安装)的完整案例。通过该案例,当VM1与VM2首次通信时,Ryu控制器会动态学习路径并下发流表,后续流量将直接由交换机转发,无需控制器介…...

动手学深度学习2025.2.23-预备知识之-线性代数
3.线性代数 (1)向量维数和张量维数的区别: (2)普通矩阵乘法: 要求左矩阵的列数等于右矩阵的行数 import torch # 创建两个矩阵 A torch.tensor([[1, 2], [3, 4]], dtypetorch.float32) B torch.tensor([[5, 6], [7, 8]], d…...
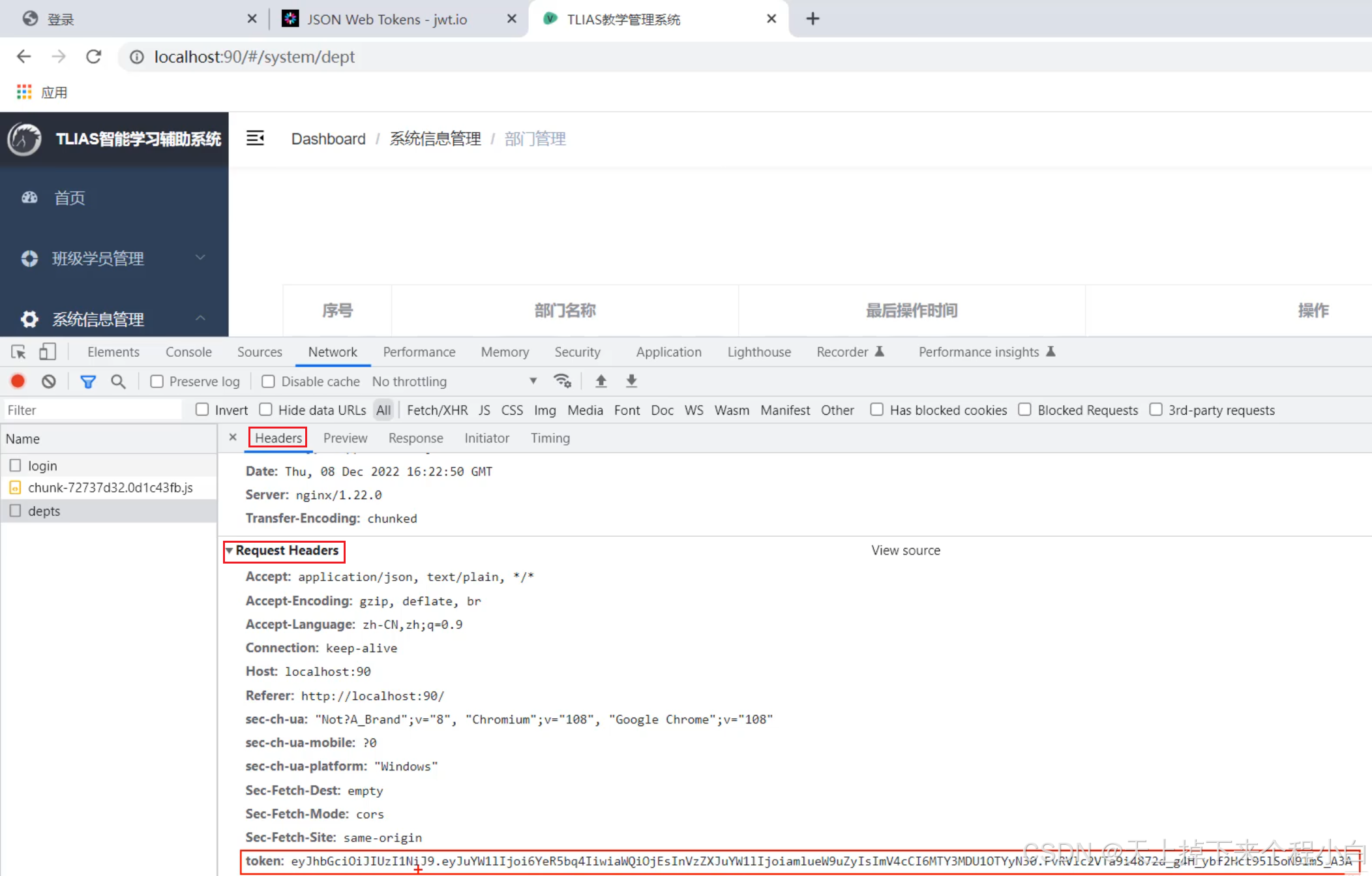
登录-07.JWT令牌-登录后下发令牌
一.思路 我们首先完成令牌生成。 在响应数据这一块 该响应数据是一个标准的Result结构,其中"data"的值就是一个JWT令牌。因此我们只需要将生成的JWT令牌封装在Result当中然后返回给前端即可。 备注是给前端看的,不用管。以后我们做校验时&…...

机器学习实战(7):聚类算法——发现数据中的隐藏模式
第7集:聚类算法——发现数据中的隐藏模式 在机器学习中,聚类(Clustering) 是一种无监督学习方法,用于发现数据中的隐藏模式或分组。与分类任务不同,聚类不需要标签,而是根据数据的相似性将其划…...

【数据序列化协议】Protocol Buffers
一、为什么需要序列化? 数据跨平台/语言交互: 不同编程语言(如 Java、Python、Go)的数据结构不兼容,序列化提供统一的数据表示。例如:Java 的 HashMap 和 Python 的 dict 需转换为通用格式(如 …...

基于 Python 的电影市场预测分析系统设计与实现(源码 + 文档)
大家好,今天要和大家聊的是一款基于 Python 的“电影市场预测分析”系统的设计与实现。项目源码以及部署相关事宜请联系我,文末附上联系方式。 项目简介 基于 Python 的“电影市场预测分析”系统主要面向以下用户角色:电影制片方、电影发行…...

计算机三级网络技术知识汇总【6】
第六章 交换机及其配置 1. 交换机基础 1.1 基本概念 局域网交换机是一种基于 MAC 地址识别,完成转发数据帧功能的一种网络连接设备。 工作在数据链路层,根据进入端口数据帧中的 MAC 地址进行数据帧的过滤、转发(也是交换机的工作原理&…...
)
2025教育与科研领域实战全解析:DeepSeek赋能细分场景深度指南(附全流程案例与资源)
🚀 2025教育与科研领域实战全解析:DeepSeek赋能细分场景深度指南(附全流程案例与资源)🚀 📚 目录 DeepSeek在教育与科研中的核心价值教学场景应用:从备课到课堂管理的全流程革新科研场景应用:从数据分析到论文写作的智能跃迁师生协同创新:AI赋能的个性化学习与科研…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
