AcWing 1230.K倍区间
AcWing 1230. K倍区间
题目描述
给定一个长度为 NNN 的数列,A1,A2,…ANA_1, A_2, … A_NA1,A2,…AN ,如果其中一段连续的子序列 Ai,Ai+1,…AjA_i, A_{i+1}, … A_jAi,Ai+1,…Aj 之和是 KKK 的倍数,我们就称这个区间 [i,j][i,j][i,j] 是 KKK 倍区间。
你能求出数列中总共有多少个 KKK 倍区间吗?
输入格式
第一行包含两个整数 NNN 和 KKK。
以下 NNN 行每行包含一个整数 AiA_iAi。
输出格式
输出一个整数,代表 KKK 倍区间的数目。
数据范围
1≤N,K≤1000001≤N,K≤1000001≤N,K≤100000,
1≤Ai≤1000001≤A_i≤1000001≤Ai≤100000
输入样例:
5 2
1
2
3
4
5
输出样例:
6
思路
求区间 [l,r][l,r][l,r] 的和是 kkk 的倍数的个数。
求区间和,我们可以通过 前缀和 来求出。
定义 sum[i] 表示第 111 个元素到第 iii 个元素的和,那么 s[r] - s[l-1] 就是区间 [l,r][l,r][l,r] 的和。
若满足条件:区间 [l,r][l,r][l,r] 的和是k的倍数,即 (s[r] - s[l-1]) % k == 0 ,等价于 s[r] % k == s[l-1] % k 。
说人话,这也就意味着:
如果
s[r] mod k和s[l - 1] mod k的余数相等,那么s[r] - s[l - 1]的差值必然是 kkk 的倍数。比如:13 % 7 == 20 % 7,则 (20 - 7) % 7 == 0
那么题目就是要我们求 前缀和%k==0 的组合有多少种。
用 cnt[i] 存储目前为止前缀和相同的个数,iii 表示这个前缀和的值。
每次用 res 来递加 cnt[i] 相同的个数,前面有几个 前缀和的值 和 当前前缀和 相等,那么这个前缀和就能和前面每一个组成一个组合,所以要 res += cnt[s[i]] ,然后再加上现在的前缀和,即 cnt[s[i]]++ 。
初始化 cnt[0] = 1 ,因为当 s[i] == 0 时,这个前缀和本身就是 kkk 的倍数,不需要再跟别的前缀和组合,计算结果时就要加上这一个。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
const int N = 1e5 + 10;int n, k;
ll s[N];
ll cnt[N];int main()
{cin >> n >> k;ll res = 0;cnt[0] = 1;for (int i = 1; i <= n; i++){cin >> s[i];s[i] = (s[i] + s[i - 1]) % k; //每次前缀和都取模res += cnt[s[i]]; //和前面每一个都组合一下cnt[s[i]]++; //现在又多了一个}cout << res << endl;return 0;
}
相关文章:

AcWing 1230.K倍区间
AcWing 1230. K倍区间 题目描述 给定一个长度为 NNN 的数列,A1,A2,…ANA_1, A_2, … A_NA1,A2,…AN ,如果其中一段连续的子序列 Ai,Ai1,…AjA_i, A_{i1}, … A_jAi,Ai1,…Aj 之和是 KKK 的倍数,我们就称这个区间 [i,j][i,j][i,…...
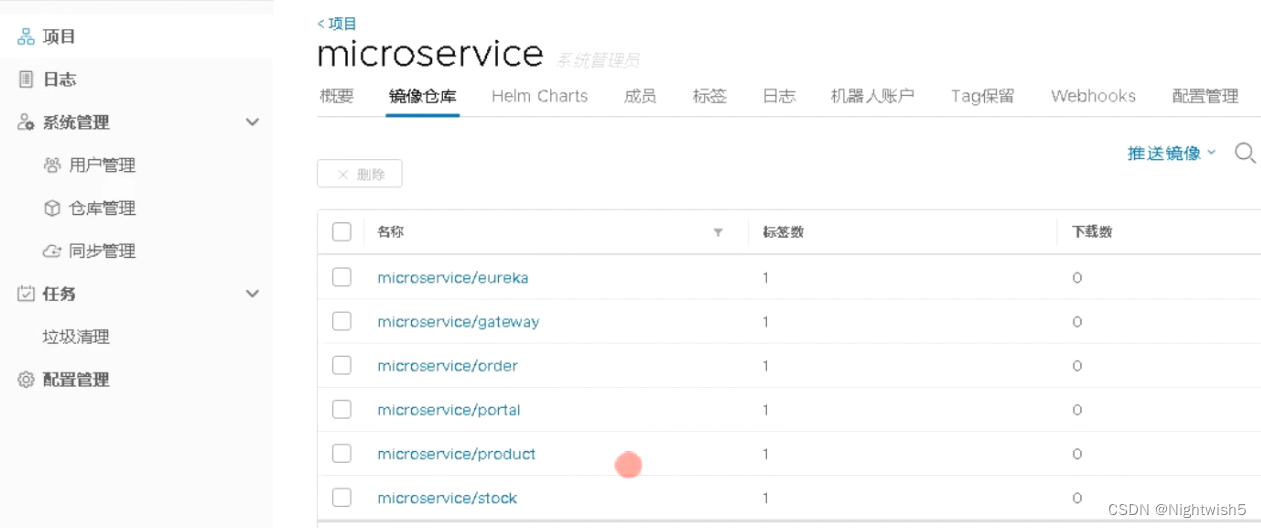
kubernetes集群部署springcloud项目【AL】【未写完】
kubernetes集群部署springcloud项目【AL】 (先手工做,非自动化) #环境: 192.168.73.138 master 192.168.73.139 node1 192.168.73.140 node2 192.168.73.137 harbor、mysqlgit clone https://github.com/lizhenliang/simple-…...
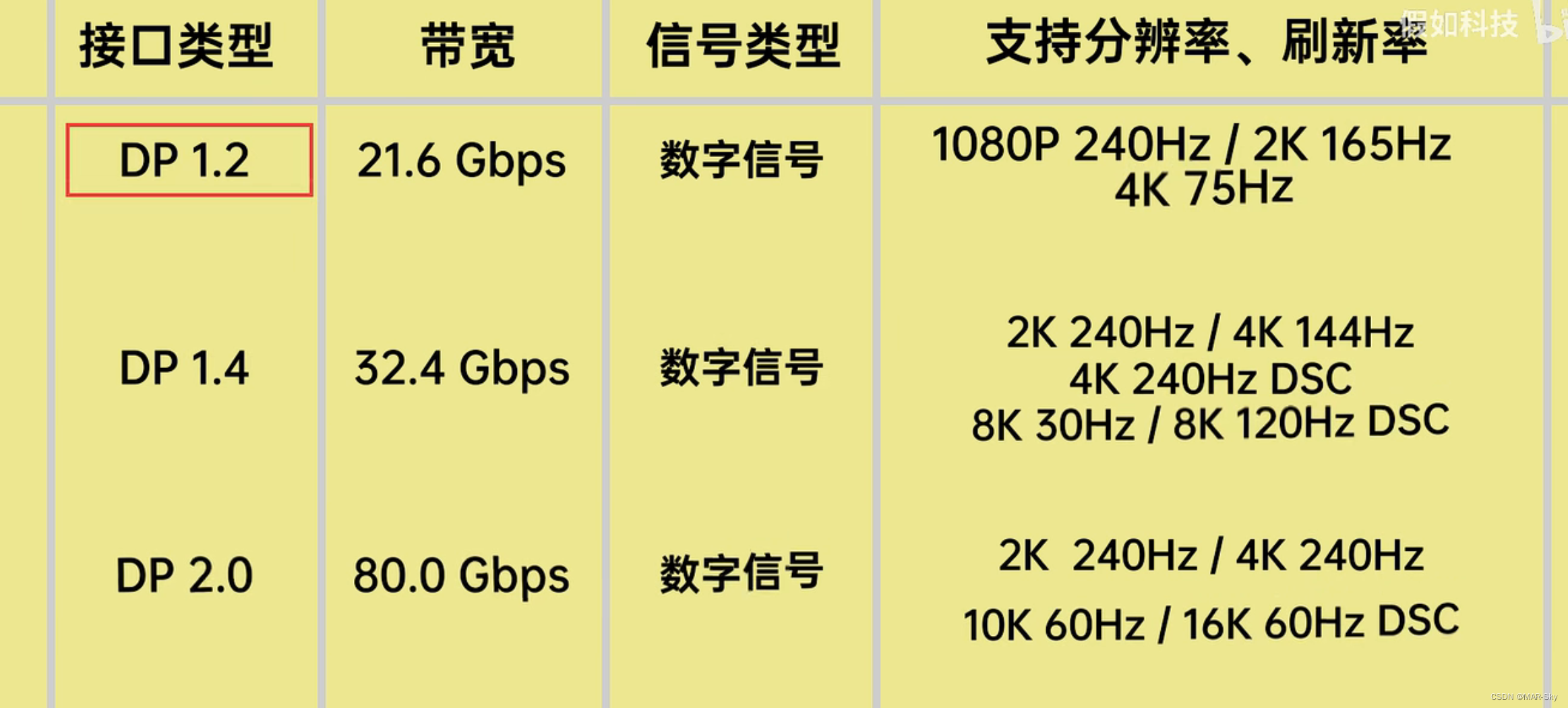
各种音频接口比较
时间 参考:https://www.bilibili.com/video/BV1SL4y1q7GZ/?spm_id_from333.337.search-card.all.click&vd_source00bd76f9d6dc090461cddd9f0deb2d51, https://blog.csdn.net/weixin_43794311/article/details/128941346 接口名字时间公司支持格式…...
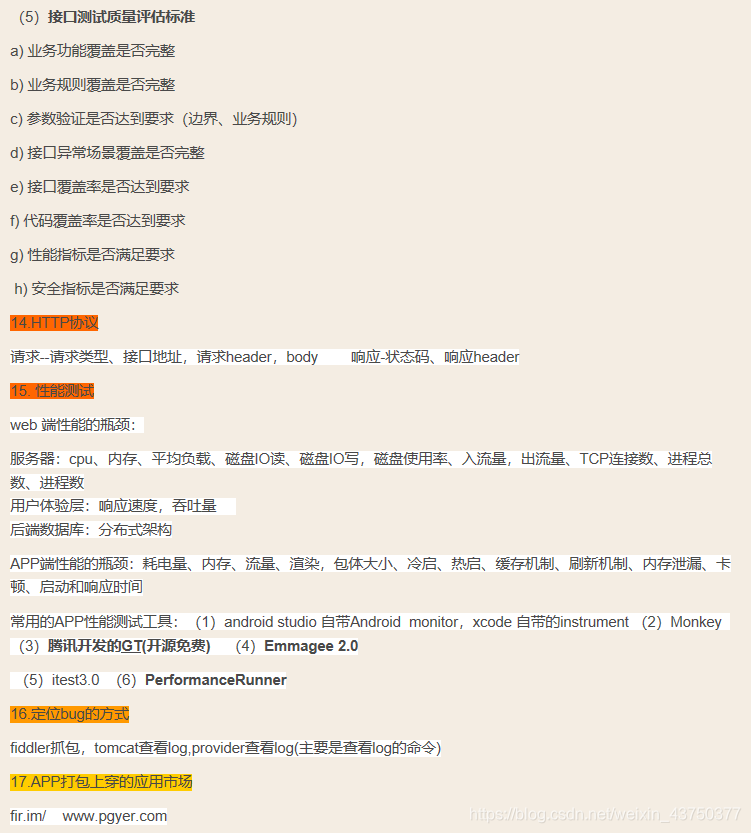
软件测试面试理论(超详细)
【面试理论知识】1、你的测试职业发展是什么? 测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前3年积累测试经验,按如何做好测试工程师的要点去要求自己…...
)
c++学习笔记-二进制文件操作(哔站-黑马程序员c++教学视频)
一、基本概念 以二进制的方式对文件进行读写操作 打开方式指定为 ios::binary 优点:可以写入自己定义的数据类型 1、写文件 二进制方式写文件:流对象调用成员write 函数原型:ostream& write(const char * buffer,int len);参数解释…...

内网渗透(二十三)之Windows协议认证和密码抓取-Mimikatz介绍和各种模块使用方法
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Nginx if的使用教程
if指令该指令用来支持条件判断,并根据条件判断结果选择不同的Nginx配置。语法if (condition){...}默认值—位置server、locationcondition为判定条件,可以支持以下写法:1. 变量名。如果变量名对应的值为空字符串或"0",i…...
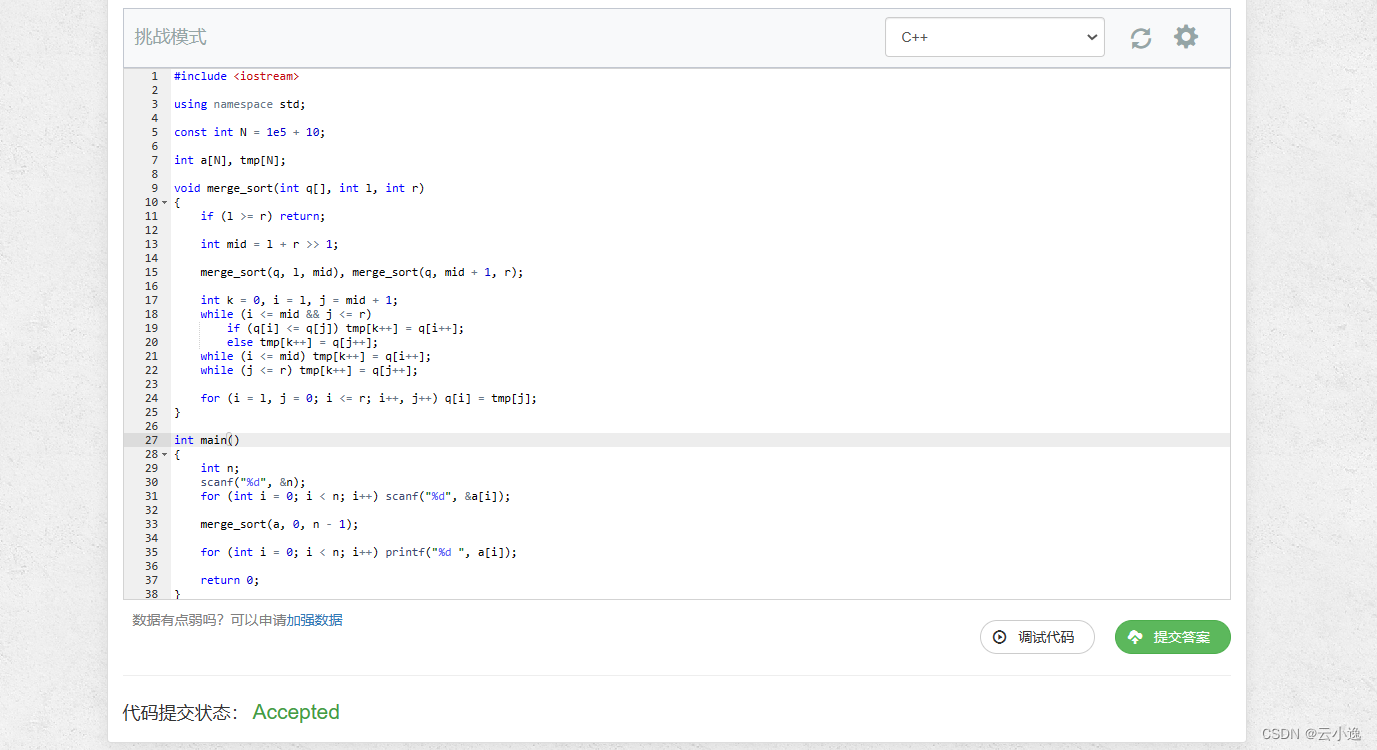
备考蓝桥杯【快速排序和归并排序】
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Taro使用微信OCR插件无法调用onSuccess回调问题
Taro使用微信插件无法调用onSuccess回调问题小程序后台添加插件在开放社区购买相应的套餐详细步骤1.在app.config.js中添加如下代码2.在页面的page.config.js添加插件3.使用ocr-navigator识别身份证小程序后台添加插件 在开放社区购买相应的套餐 购买地址 详细步骤 1.在app.…...
【Java】代码块的细节你搞懂了吗(基础知识七)
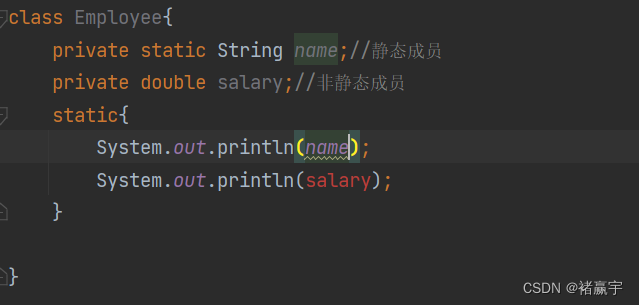
希望像唠嗑一样,one step one futher。 目录 (1)代码块的应用场景 (2)代码块的细节 1.static 代码块只加载一次 2.当调用类的静态成员时,类会加载 3. 使用类的静态成员时,static代码块会被执…...
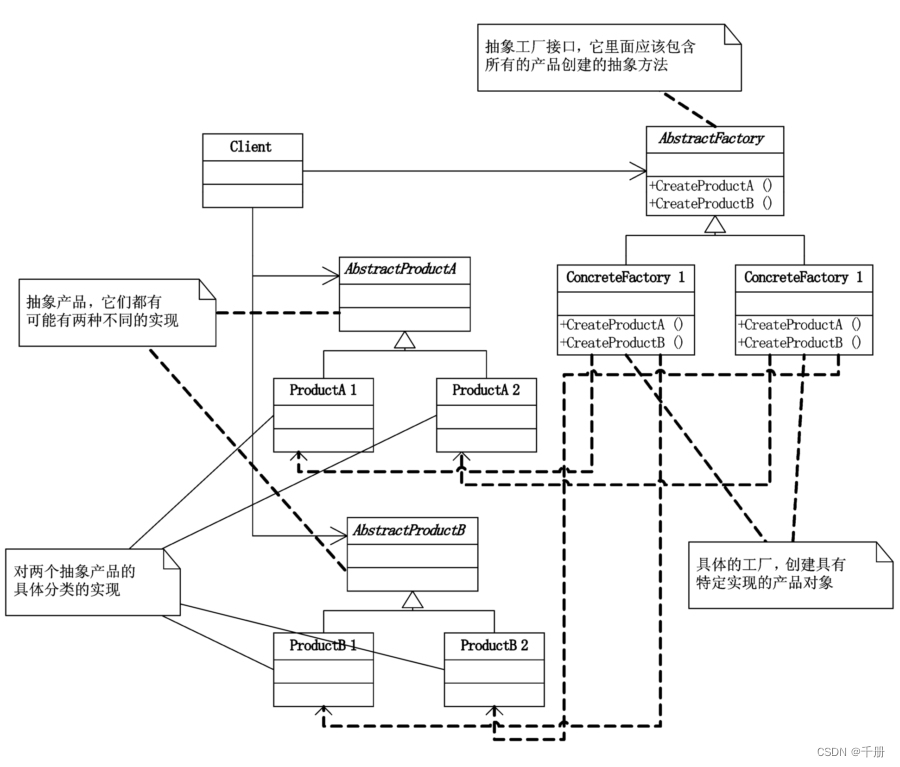
设计模式C++实现12:抽象工厂模式
参考大话设计模式; 详细内容参见大话设计模式一书第十五章,该书使用C#实现,本实验通过C语言实现。 抽象工厂模式(Abstract Factory),提供一个创建一系列相关或相互依赖对象的接口,而无需指定它们…...
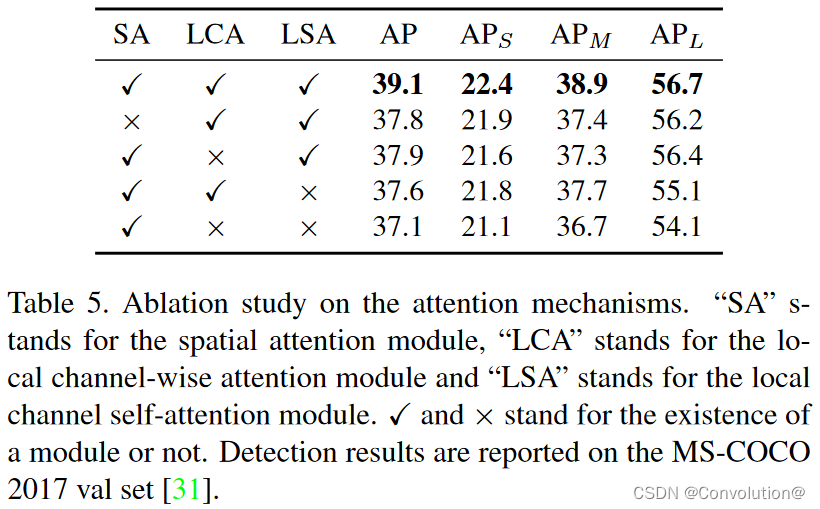
目标检测论文阅读:GraphFPN算法笔记
标题:GraphFPN: Graph Feature Pyramid Network for Object Detection 会议:ICCV2021 论文地址:https://ieeexplore.ieee.org/document/9710561/ Abstract 特征金字塔已经被证明在需要多尺度特征的图像理解任务中是强大的。SOTA的多尺度特征…...
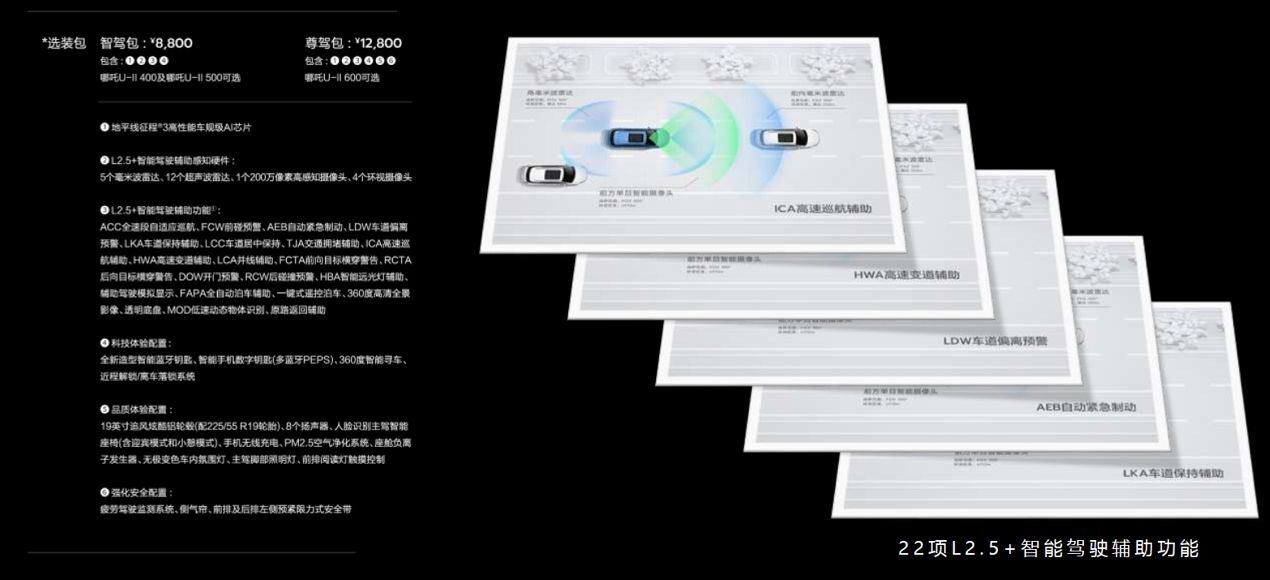
实测2023款哪吒U-II,智驾功能对女司机很友好
最近,我们受邀试驾了2023款哪吒U-II。这是一款A级新能源SUV,是哪吒U的改款车型。哪吒U系列自2020年3月上市到2023年1月,累计销售数量达76688台,也因此被称为15万级智能天花板。2023款哪吒U-II的一大亮点是:针对以往哪吒…...

Python自动化测试【软件测试最全教程(附笔记、学习路线)】,看完即就业
最近看到很多粉丝在后台私信我,叫我做一期Python自动化测试的教程,其实关于这个问题,我也早就在着手准备了,我录制了一整套完整的Python自动化测试的教程,上传到网盘里了,大家有兴趣的可以去文末交流群免费…...

2023/2/13总结
今天主要学习了哈夫曼树。 哈夫曼树 哈夫曼树是二叉树的一种,它是一种WPL最优二叉树。 叶子结点(也称叶节点):指的是自己下面不再连接有节点的节点(即末端),称为叶子节点(又称为终…...

webSock前端
1.什么是webSocket WebSocket是一种在单个TCP连接上进行全双工通信的协议。允许服务端主动向客户端推送数据。 2.如何使用webSocket WebSocket 构造函数WebSocket 对象作为一个构造函数,用于新建 WebSocket 实例。 代码如下: let ws = new WebSocket(网址); 2.websock事件: …...
)
AcWing 3956. 截断数组(每日一题)
AcWing 3956. 截断数组 题目描述 给定一个长度为 nnn 的数组 a1,a2,…,ana_1, a_2, …, a_na1,a2,…,an 。 现在,要将该数组从中间截断,得到三个非空子数组。 要求,三个子数组内各元素之和都相等。 请问,共有多少种不同…...

Android 一体机研发之修改系统设置————屏幕亮度
Android 一体机研发之修改系统设置————屏幕亮度 Android 一体机研发之修改系统设置————声音 Android 一体机研发之修改系统设置————自动锁屏 前言 最近工作略微有点儿空闲,抽空给大家总结一下:近期一直搞得一体机app研发,适用…...

C++通用算法
1.概述根据名字就知道如何使用相关算法,比如copy函数,就是复制的意思,它需要一个范围,以及要复制的位置copy(begin, end, container_begin);#include <iostream> #include<vector> #include<algorithm> #includ…...

Springboot停机方式
1. 介绍 简单的说,就是向应用进程发出停止指令之后,能保证正在执行的业务操作不受影响,直到操作运行完毕之后再停止服务。应用程序接收到停止指令之后,会进行如下操作: 1.停止接收新的访问请求 2.正在处理的请求&…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
