数据结构——TreeMap、TreeSet与HashMap、HashSet
目录
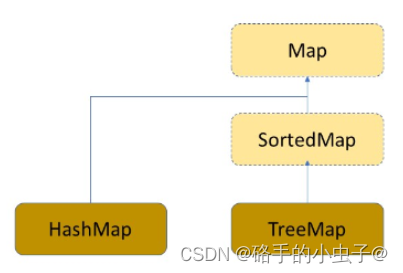
一、Map
1、定义
2、常用方法
3、注意
二、TreeMap
三、HashMap
1、定义
2、冲突定义
3、冲突避免方法——哈希函数设计
(1)、直接定制法(常用)
(2)、除留余数法(常用)
(3)、平方取中法
(4)、折叠法
(5)、随机数法
(6)、数学分析法
5、冲突避免方法——闭散列
(1)、线性探测
(2)、线性探测
6、冲突避免方法——开散列/哈希桶
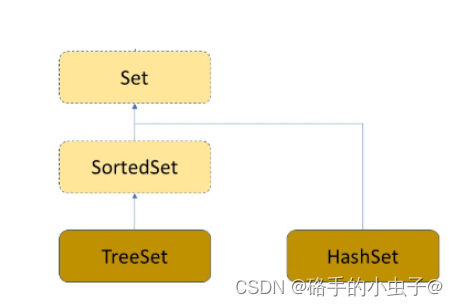
四、Set
1、定义
2、常用方法
3、注意
五、TreeSet
六、HashSet
一、Map
1、定义
Map是一个接口类,该类没有继承自Collection,该类中存储的是<K,V>结构的键值对,并且K一定是唯一的,不能重复。
2、常用方法
V get(Object key)返回 key 对应的 value
V getOrDefault(Object key, V defaultValue)返回 key 对应的 value,key 不存在,返回默认值
V put(K key, V value)设置 key 对应的 value
V remove(Object key)删除 key 对应的映射关系
Set<K> keySet()返回所有 key 的不重复集合
Collection<V> values()返回所有 value 的可重复集合
Set<Map.Entry<K, V>> entrySet()返回所有的 key-value 映射关系
boolean containsKey(Object key)判断是否包含 key
boolean containsValue(Object value)判断是否包含 value
3、注意
- Map是一个接口,不能直接实例化对象,如果要实例化对象只能实例化其实现类TreeMap或者HashMap
- Map中存放键值对的Key是唯一的,value是可以重复的
- 在TreeMap中插入键值时,key不能为空,否则就会抛NullPointerException异常,value可以为空。但是HashMap的key和value都可以为空。
- Map中的Key可以全部分离出来,存储到Set中来进行访问(因为Key不能重复)。
- Map中的value可以全部分离出来,存储在Collection的任何一个子集合中(value可能有重复)。
- Map中键值对的Key不能直接修改,value可以修改,如果要修改key,只能先将该key删除掉,然后再来进行重新插入。
二、TreeMap
里面是一个集合 ,TreeMap的底层代码是一个Map集合接口
| Map底层结构 | TreeMap |
| 底层结构 | 红黑树 |
| 插入/删除/查找时间复杂度 | O(1) |
| 是否有序 | 关于Key有序 |
| 线程安全 | 不安全 |
| 插入/删除/查找区别 | 需要进行元素比较 |
| 比较与覆写 | key必须能够比较,否则会抛ClassCastException异常 |
| 应用场景 | 需要Key有序场景下 |
三、HashMap
1、定义
不经过任何比较,一次直接从表中得到要搜索的元素。 如果构造一种存储结构,通过某种函
数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
| Set底层结构 | HashSet |
| 底层结构 | 哈希桶 |
| 插入/删除/查找时间复杂度 | O(1) |
| 是否有序 | 不一定有序 |
| 线程安全 | 不安全 |
| 插入/删除/查找区别 | 先计算key哈希地址,然后进行插入和删除 |
| 比较与覆写 | 自定义类型需要覆写equals和hashCode方法 |
| 应用场景 | key是否有序不关心,需要更高的时间性能 |
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即O(log2N),搜索的效率取决于搜索过程中元素的比较次数。
- 插入元素:根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
- 搜索元素:对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功。
该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(HashTable)(或者称散列表)
2、冲突定义
对于两个数据元素的关键字 和 (i != j),有 != ,但有:Hash( ) == Hash( ),即:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
3、冲突避免方法——哈希函数设计
哈希表底层数组的容量往往是小于实际要存储的关键字的数量的,因此冲突的发生是必然的,所以我们能做的应该是尽量的降低冲突率。
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
(1)、直接定制法(常用)
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B 优点:简单、均匀 缺点:需要事先知道关键字的分布情况 使用场景:适合查找比较小且连续的情况 面试题:字符串中第一个只出现一次字符
(2)、除留余数法(常用)
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址
(3)、平方取中法
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址; 再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况
(4)、折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
(5)、随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数函数。通常应用于关键字长度不等时采用此法
(6)、数学分析法
设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均匀的情况
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
5、冲突避免方法——闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢?
(1)、线性探测
比如上面的场景,现在需要插入元素44,先通过哈希函数计算哈希地址,下标为4,因此44理论上应该插在该位置,但是该位置已经放了值为4的元素,即发生哈希冲突。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
插入
- 通过哈希函数获取待插入元素在哈希表中的位置
- 如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素
- 采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。
(2)、线性探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为:Hi=(H0+i^2)%m,或者:Hi=(H0-i^2)%m。其中i,2,3...,H0是通过散列函数Hash(x)对元素的关键码key进行计算得到的位置,m是表的大小。
因此:比散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷
6、冲突避免方法——开散列/哈希桶
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
开散列中每个桶中放的都是发生哈希冲突的元素,开散列,可以认为是把一个在大集合中的搜索问题转化为在小集合中做搜索了
四、Set
1、定义
Set是继承自Collection的一个接口类,Set中只存储了key,并且要求key一定要唯一。Set最大的功能就是对集合中的元素进行去重
2、常用方法
boolean add(E e) 添加元素,但重复元素不会被添加成功
void clear() 清空集合
boolean contains(Object o) 判断 o 是否在集合中
Iterator<E> iterator()
返回迭代器
boolean remove(Object o)
删除集合中的 o
int size() 返回set中元素的个数
boolean isEmpty()
检测set是否为空,空返回true,否则返回false
Object[] toArray()
将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)
集合c中的元素是否在set中全部存在,是返回true,否则返回false
boolean addAll(Collection<? extends E> c)将集合c中的元素添加到set中,可以达到去重的效果
3、注意
- TreeSet的底层是使用Map来实现的,其使用key与Object的一个默认对象作为键值对插入到Map中的
- 实现Set接口的常用类有TreeSet和HashSet,还有一个LinkedHashSet,LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。
- Set中的Key不能修改,如果要修改,先将原来的删除掉,然后再重新插入
- TreeSet中不能插入null的key,HashSet可以。
- TreeSet和HashSet的区别
五、TreeSet
TreeSet的底层是TreeMap,去掉重复的元素,key的重复不会再搜索树中出现
TreeSet继承了Set,Set又继承了Collection
| Set底层结构 | TreeMap |
| 底层结构 | 红黑树 |
| 插入/删除/查找时间复杂度 | O(log2N) |
| 是否有序 | 关于Key有序 |
| 线程安全 | 不安全 |
| 插入/删除/查找区别 | 按照红黑树的特性来进行插入和删除 |
| 比较与覆写 | key必须能够比较,否则会抛出ClassCastException异常 |
| 应用场景 | 需要Key有序场景下 |
注:
将Map与Set联系起来Set<Map.Entry<String,Integer>> entries=map.entrySet();才能使用Iterable中迭代打印,foreach打印等方法,Map一系中是独立出来并没有实现在下面的关系图中,TreeSet弥补了当前的缺陷。
六、HashSet
| Set底层结构 | HashSet |
| 底层结构 | 哈希桶 |
| 插入/删除/查找时间复杂度 | O(1) |
| 是否有序 | 不一定有序 |
| 线程安全 | 不安全 |
| 插入/删除/查找区别 | 先计算key哈希地址,然后进行插入和删除 |
| 比较与覆写 | 自定义类型需要覆写equals和hashCode方法 |
| 应用场景 | key是否有序不关心,需要更高的时间性能 |
相关文章:

数据结构——TreeMap、TreeSet与HashMap、HashSet
目录 一、Map 1、定义 2、常用方法 3、注意 二、TreeMap 三、HashMap 1、定义 2、冲突定义 3、冲突避免方法——哈希函数设计 (1)、直接定制法(常用) (2)、除留余数法(常用) (3)、平方取中法 &…...
Spring Boot学习篇(十三)
Spring Boot学习篇(十三) shiro安全框架使用篇(五) 1 准备工作 1.1 在SysUserMapper.xml中书写自定义标签 <select id"findRoles" resultType"string">select name from sys_role where id (select roleid from sys_user_role where userid (S…...

微软Bing的AI人工只能对话体验名额申请教程
微软Bing 免费体验名额申请教程流程ChatGPT这东西可太过火了。国外国内,圈里圈外都是人声鼎沸。微软,谷歌,百度这些大佬纷纷出手。连看个同花顺都有GPT概念了,搞技术,做生意的看来都盯上了 流程 下面就讲一下如何申…...
怎么打造WhatsApp Team?SaleSmartly(ss客服)告诉你
关键词:WhatsApp Team SaleSmartly(ss客服) 您是否正在寻找一种让您的团队能够在 WhatsApp协作消息传递的解决方案?拥有了 WhatsApp Team,不仅效率提升,还可以在智能聊天工具中比如SaleSmartly(ss客服&…...

IPV4地址的原理和配置
第三章:IP地址的配置 IPv4(Internet Protocol Version 4)协议族是TCP/IP协议族中最为核心的协议族。它工作在TCP/IP协议栈的网络层,该层与OSI参考模型的网络层相对应。网络层提供了无连接数据传输服务,即网络在发送分…...
软件测试面试准备——(一)Selenium(1)基础问题及自动化测试
滴滴面试:1. 自己负责哪部分功能?农餐对接系统分为了两大子系统,一个是个人订餐系统,二是餐馆、个人与农产品供应商进行农产品交易系统。我主要负责组织测试人员对该系统进行测试。我们测试分为两个阶段:一、功能测试阶…...

AcWing 1230.K倍区间
AcWing 1230. K倍区间 题目描述 给定一个长度为 NNN 的数列,A1,A2,…ANA_1, A_2, … A_NA1,A2,…AN ,如果其中一段连续的子序列 Ai,Ai1,…AjA_i, A_{i1}, … A_jAi,Ai1,…Aj 之和是 KKK 的倍数,我们就称这个区间 [i,j][i,j][i,…...
kubernetes集群部署springcloud项目【AL】【未写完】
kubernetes集群部署springcloud项目【AL】 (先手工做,非自动化) #环境: 192.168.73.138 master 192.168.73.139 node1 192.168.73.140 node2 192.168.73.137 harbor、mysqlgit clone https://github.com/lizhenliang/simple-…...
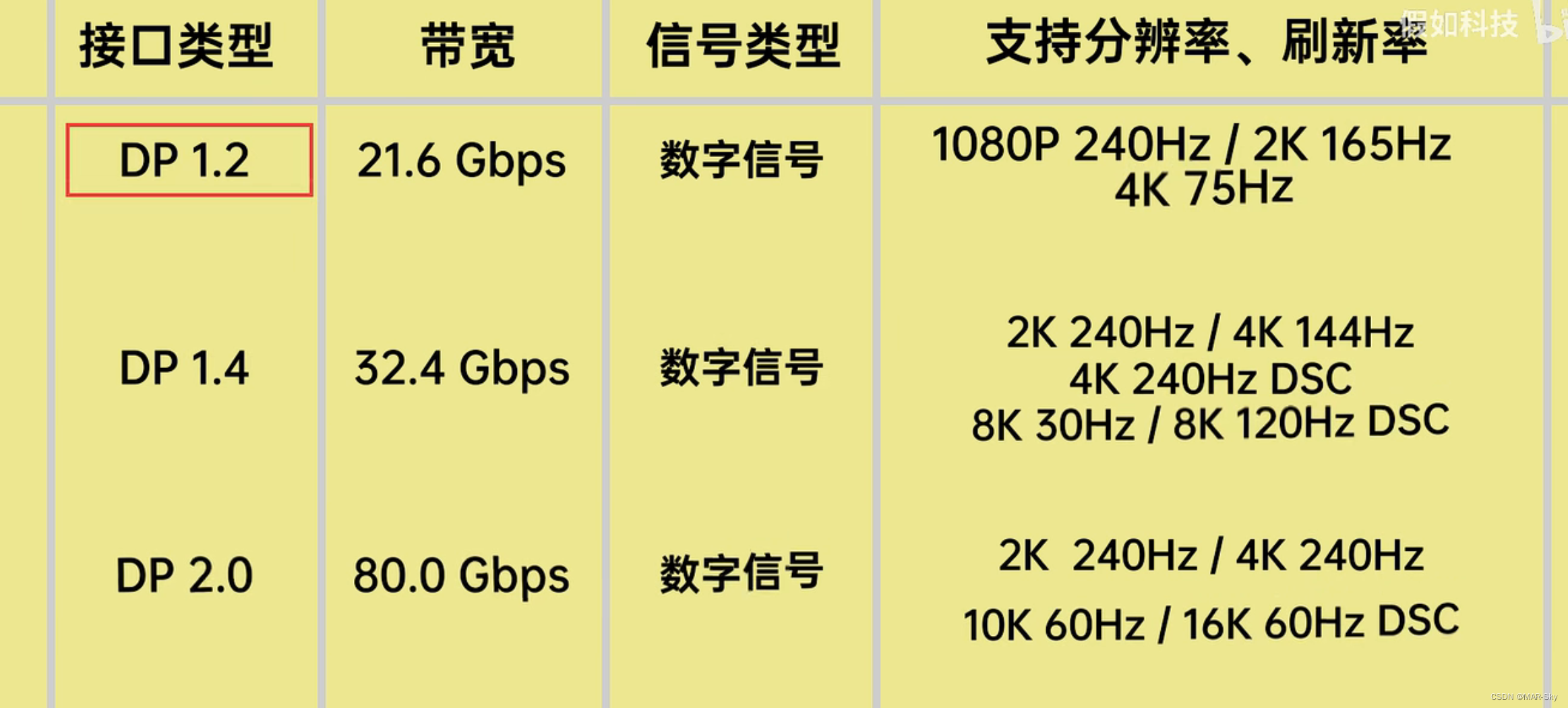
各种音频接口比较
时间 参考:https://www.bilibili.com/video/BV1SL4y1q7GZ/?spm_id_from333.337.search-card.all.click&vd_source00bd76f9d6dc090461cddd9f0deb2d51, https://blog.csdn.net/weixin_43794311/article/details/128941346 接口名字时间公司支持格式…...
软件测试面试理论(超详细)
【面试理论知识】1、你的测试职业发展是什么? 测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前3年积累测试经验,按如何做好测试工程师的要点去要求自己…...
)
c++学习笔记-二进制文件操作(哔站-黑马程序员c++教学视频)
一、基本概念 以二进制的方式对文件进行读写操作 打开方式指定为 ios::binary 优点:可以写入自己定义的数据类型 1、写文件 二进制方式写文件:流对象调用成员write 函数原型:ostream& write(const char * buffer,int len);参数解释…...

内网渗透(二十三)之Windows协议认证和密码抓取-Mimikatz介绍和各种模块使用方法
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Nginx if的使用教程
if指令该指令用来支持条件判断,并根据条件判断结果选择不同的Nginx配置。语法if (condition){...}默认值—位置server、locationcondition为判定条件,可以支持以下写法:1. 变量名。如果变量名对应的值为空字符串或"0",i…...
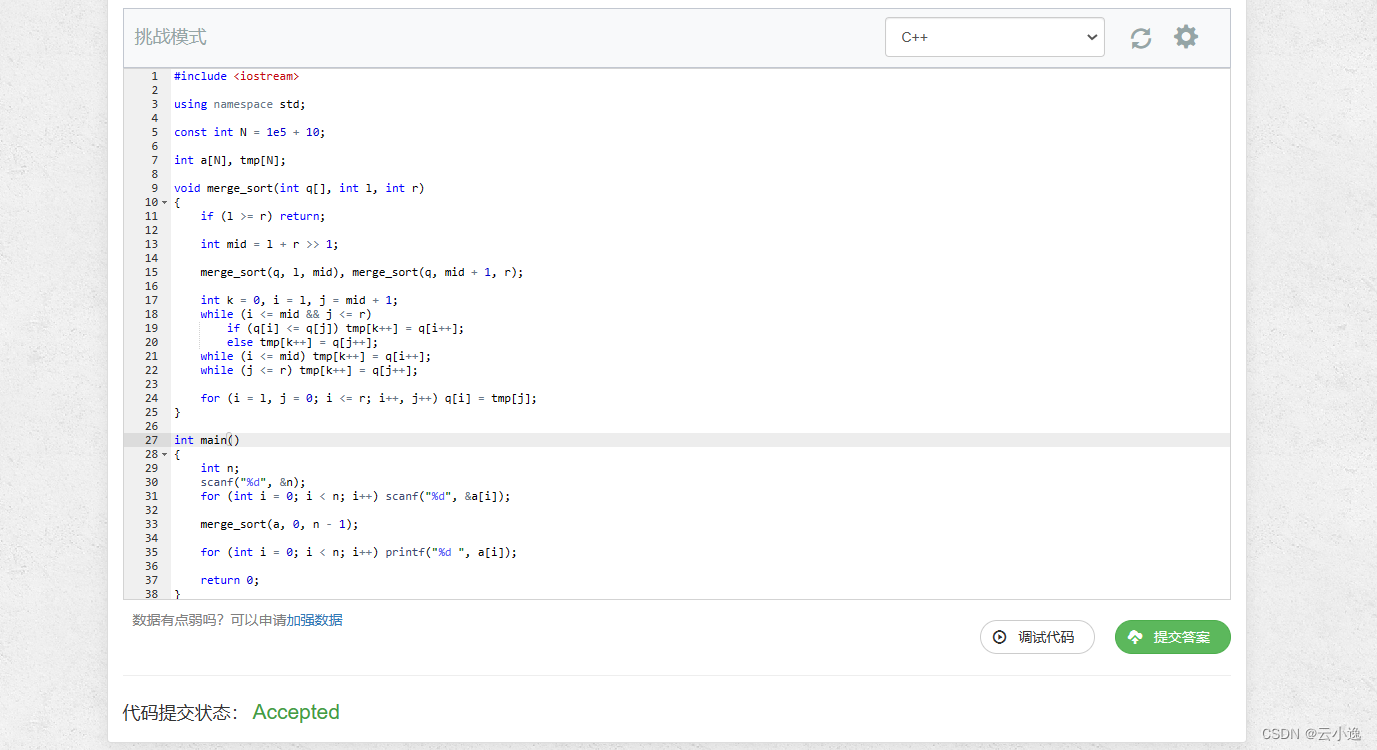
备考蓝桥杯【快速排序和归并排序】
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Taro使用微信OCR插件无法调用onSuccess回调问题
Taro使用微信插件无法调用onSuccess回调问题小程序后台添加插件在开放社区购买相应的套餐详细步骤1.在app.config.js中添加如下代码2.在页面的page.config.js添加插件3.使用ocr-navigator识别身份证小程序后台添加插件 在开放社区购买相应的套餐 购买地址 详细步骤 1.在app.…...
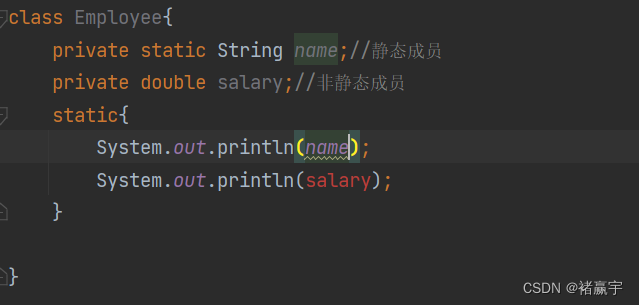
【Java】代码块的细节你搞懂了吗(基础知识七)
希望像唠嗑一样,one step one futher。 目录 (1)代码块的应用场景 (2)代码块的细节 1.static 代码块只加载一次 2.当调用类的静态成员时,类会加载 3. 使用类的静态成员时,static代码块会被执…...
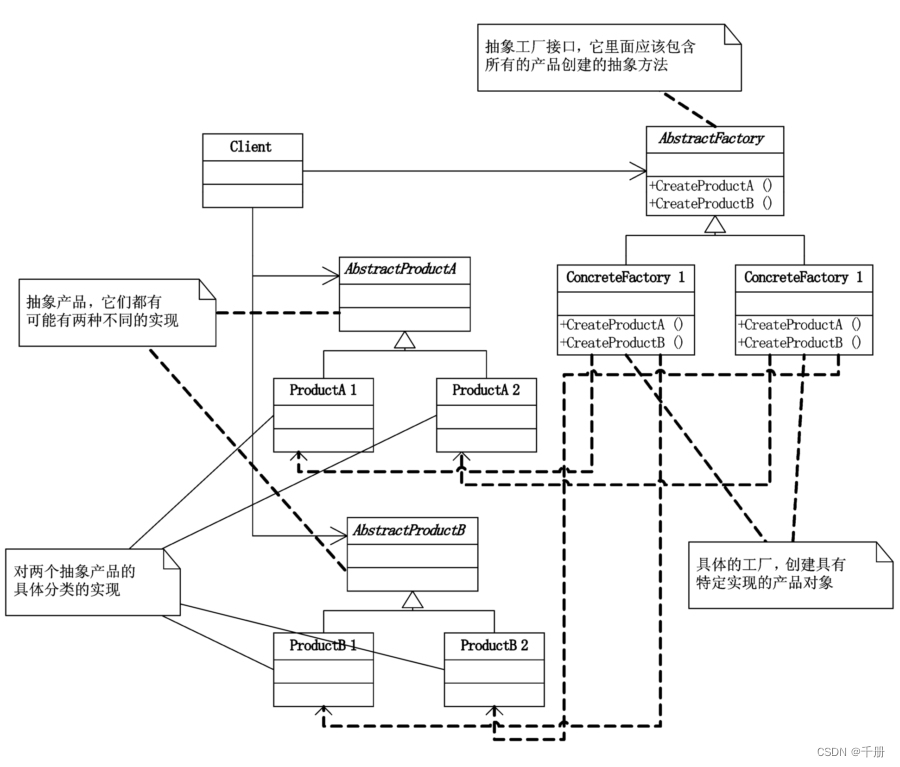
设计模式C++实现12:抽象工厂模式
参考大话设计模式; 详细内容参见大话设计模式一书第十五章,该书使用C#实现,本实验通过C语言实现。 抽象工厂模式(Abstract Factory),提供一个创建一系列相关或相互依赖对象的接口,而无需指定它们…...
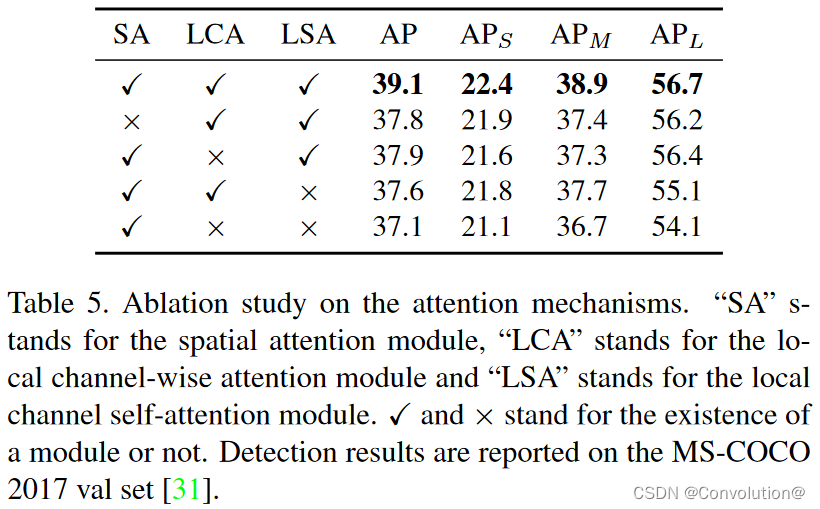
目标检测论文阅读:GraphFPN算法笔记
标题:GraphFPN: Graph Feature Pyramid Network for Object Detection 会议:ICCV2021 论文地址:https://ieeexplore.ieee.org/document/9710561/ Abstract 特征金字塔已经被证明在需要多尺度特征的图像理解任务中是强大的。SOTA的多尺度特征…...
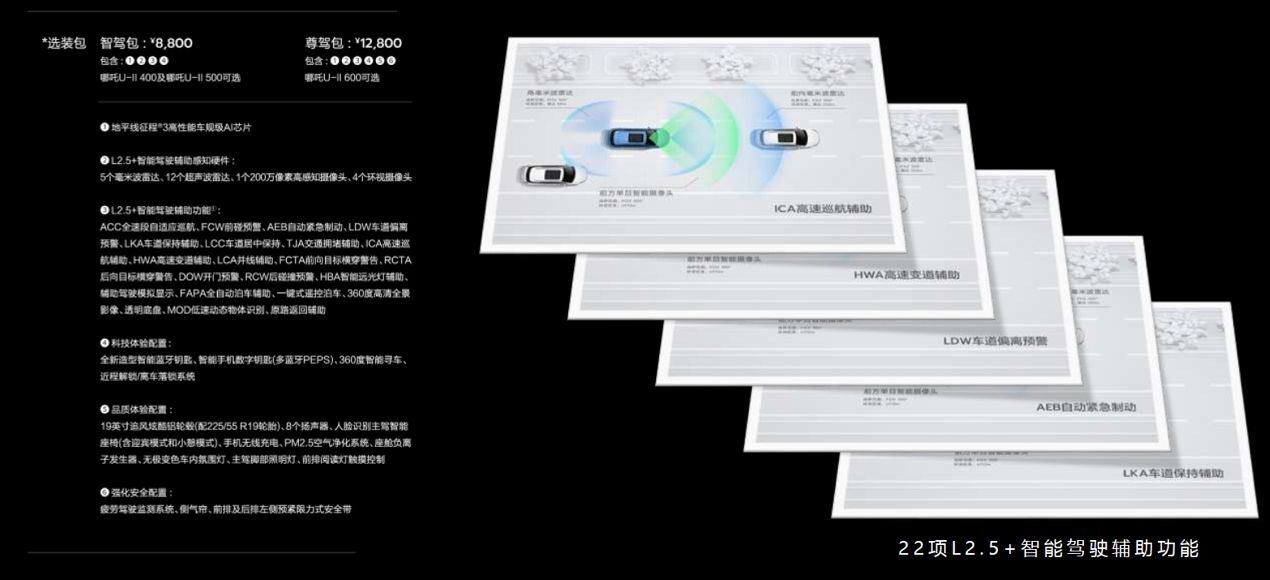
实测2023款哪吒U-II,智驾功能对女司机很友好
最近,我们受邀试驾了2023款哪吒U-II。这是一款A级新能源SUV,是哪吒U的改款车型。哪吒U系列自2020年3月上市到2023年1月,累计销售数量达76688台,也因此被称为15万级智能天花板。2023款哪吒U-II的一大亮点是:针对以往哪吒…...

Python自动化测试【软件测试最全教程(附笔记、学习路线)】,看完即就业
最近看到很多粉丝在后台私信我,叫我做一期Python自动化测试的教程,其实关于这个问题,我也早就在着手准备了,我录制了一整套完整的Python自动化测试的教程,上传到网盘里了,大家有兴趣的可以去文末交流群免费…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
