第16届蓝桥杯模拟赛3 python组个人题解
第16届蓝桥杯模拟赛3 python组
思路和答案不保证正确
1.填空
如果一个数 p 是个质数,同时又是整数 a 的约数,则 p 称为 a 的一个质因数。
请问, 2024 的最大的质因数是多少?
因为是填空题,所以直接枚举2023~2 ,第一个即是质数也是2024的因数的数就是答案。
def isprime(x):for i in range(2,int(x ** 0.5)+1):if(x % i == 0):return Falsereturn True
for i in range(2023,1,-1):if(2024 % i == 0 and isprime(i)):print(i)
# 23
# 11
# 2
2.填空
对于两个整数 a, b,既是 a 的整数倍又是 b 的整数倍的数称为 a 和 b 的公倍数。公倍数中最小的正整数称为 a 和 b 的最小公倍数。
请问, 2024 和 1024 的最小公倍数是多少?
经典求lcm: l c m ( a , b ) = a ∗ b g c d ( a ∗ b ) lcm(a,b) = \frac{a * b}{ gcd(a* b)} lcm(a,b)=gcd(a∗b)a∗b
def gcd(x,y):if(y == 0): return xreturn gcd(y,x % y)
def lcm(x,y):return x * y // gcd(x,y)
print(lcm(2024,1024))
## 259072
(python3.9版本以后的math库中含有lcm函数可以直接调用)
import math
print(math.lcm(2024,1024))
## 259072
3.填空
如果一个数 p 是个质数,同时又是整数 a 的约数,则 p 称为 a 的一个质因数。
请问, 2024 的所有质因数的和是多少?
第一个填空使用的代码已经计算出了2024的质因数为:23,11,8,4,2 ,加到一起就可以了
def isprime(x):for i in range(2,int(x ** 0.5)+1):if(x % i == 0):return Falsereturn True
s = 0
for i in range(2023,1,-1):if(2024 % i == 0 and isprime(i)):s = s + i
print(s)
## 36
4.填空
请问,在不超过 2024 的数中,最大的质数是多少?
枚举2023~2,找到第一个质数
def isprime(x):for i in range(2,int(x ** 0.5)+1):if(x % i == 0):return Falsereturn True
s = 0
for i in range(2023,1,-1):if(isprime(i)):print(i)break
## 2017
5.填空
如果两个整数 a, b 除了 1 以外,没有其它的公约数,则称整数 a 与 b 互质。
请问,与 2024 互质的数中(包括1),第 2024 小的数是多少?
while循环从1开始找满足 g c d ( x , 2024 ) = = 1 gcd(x,2024) == 1 gcd(x,2024)==1 的数,找第2024个
def gcd(x,y):if(y == 0): return xreturn gcd(y,x % y)
cnt = 0
p = 0
while(cnt < 2024):p += 1if(gcd(p,2024) == 1):cnt += 1
print(p)
## 4655
6.填空
对于字符串 S=ANQNANBNQNANQNQNBNINQNQNANQNINANQNANBNQNANQNQNBNBNQNQNANQNINANQNANBNQNANQNQNBNINQNQNANQNINBNQNANBNQN ,请找到 S 的一个长度不超过 10 的子串 A,使得(A的长度)乘以(A在S中出现的次数)最大。
请问这个子串是什么?(如果有多个满足条件的,请回答字典序最小的)。
字符串不长,直接枚举所有长度不超过10的子串,然后将他们的出现次数记录在字典中,然后在字典中找答案就好
s = "ANQNANBNQNANQNQNBNINQNQNANQNINANQNANBNQNANQNQNBNBNQNQNANQNINANQNANBNQNANQNQNBNINQNQNANQNINBNQNANBNQN"
dic = {}
for length in range(1,11):for i in range(0,len(s) - length):dic[s[i:i+length]] = dic.get(s[i:i+length],0) + 1
ansstr = ""
ansnum = 0
for s,cnt in dic.items():num = cnt * len(s)if(num > ansnum) or (num == ansnum and s < ansstr):ansstr = sansnum = num
print(ansstr)
# NQN
7.填空
如果一个字符串中只包含字符 0 和字符 1,则称为一个 01 串(包含全为 0 的串和全为 1 的串)。
请问有多少个长度为 24 的 01 串,满足任意 5 个连续的位置中不超过 3 个位置的值为 1 。
长度为24的01串总共有 2 24 2^{24} 224 个,大约 1.7 ∗ 1 0 7 1.7*10^7 1.7∗107 , 可以花点时间暴力枚举所有的字符串(反正是填空题)
import time
def check(x):lst = []for i in range(0,24):if(x & ( 1 << i)):lst.append(i)if(len(lst)<=2):return Truefor i in range(len(lst)-2):if(lst[i+2] - lst[i]<= 4):return Falsereturn True
ans = 0
tik = time.time()
for x in range(1<<24):# 这些01串可以用0~(2**24-1)的二进制数表示if(check(x)):ans += 1
tok = time.time()
print(tok-tik) # 花了25.859452724456787秒运行程序
print(ans) # 最终答案是162165
也可以使用dfs来解决本题:
import time
lis = [] # 存储当前数的1的位置
ans = 0
def dfs(step):global ansif(step == 25):ans += 1return if(len(lis) < 2 or step - lis[-2] > 4):lis.append(step) # 选1dfs(step + 1) lis.pop() # 还原现场dfs(step + 1) # 选0
tic = time.time()
dfs(1)
tok = time.time()
print(tok - tic)# 花了0.04025077819824219秒运行程序
print(ans) # 最终答案是162165
8. 玉米地
题意
【问题描述】
小蓝种了一块玉米地,玉米地长 n 米,宽 m 米,每平方米产玉米 a 千克。请问小蓝的玉米地一共能产多少千克玉米?
【输入格式】
输入三行。第一行包含一个正整数 n ,第二行包含一个正整数 m ,第三行包含一个正整数 a 。
【输出格式】
输出一行,包含一个整数,表示答案。
【样例输入】
20
24
900
【样例输出】
432000
【评测用例规模与约定】
对于所有评测用例,1 <= n <= 1000, 1 <= m <= 1000, 1 <= a <= 2000。
思路
直接输出 n ∗ m ∗ a n*m*a n∗m∗a
n = int(input())
m = int(input())
a = int(input())
print(n * m * a)
9.再创新高
题意
###【问题描述】
小蓝有一个数组 a[1], a[2], …, a[n], 一个“再创新高”的位置是指一个位置 p ,a[p] 的值比之前每个位置的值都大。
请求出小蓝的数组中有多少个再创新高的位置。
【输入格式】
输入的第一行包含一个整数 n 。
第二行包含 n 个整数,相邻数之间使用一个空格分隔,依次表示 a[1], a[2], …, a[n] 。
【输出格式】
输出一行,包含一个整数,表示答案。
【样例输入】
8
1 2 3 4 5 6 6 6
【样例输出】
6
【样例输入】
9
3 2 1 6 5 4 9 8 7
【样例输出】
3
【评测用例规模与约定】
对于 30% 的评测用例,1 <= n <= 100,0 <= a[i] <= 1000。
对于 60% 的评测用例,1 <= n <= 1000,0 <= a[i] <= 1000。
对于所有评测用例,1 <= n <= 10000,0 <= a[i] <= 1000000。
思路
枚举数组,不断记录max值,每当max更新就让答案加一
n = int(input())
lst = list(map(int,input().split()))
mx = -1
ans = 0
for x in lst:if(x > mx):ans += 1mx = x
print(ans)
10.四个字符串拼接
题意
【问题描述】
给定四个字符串 a, b, c, d,请将这四个字符串按照任意顺序依次连接拼成一个字符串。
请问拼成的字符串字典序最小是多少?
【输入格式】
输入四行,每行包含一个字符串。
【输出格式】
输出一行包含一个字符串,表示答案。
【样例输入】
LAN
LAN
QIAO
BEI
【样例输出】
BEILANLANQIAO
【评测用例规模与约定】
对于所有评测用例,输入的字符串非空串,由大写字母组成,长度不超过 1000 。
思路
四个字符串拼接只有 A 4 4 A_4^4 A44 种可能,直接枚举所有可能的情况,找到最小的字符串即可。
将四个字符串装入一个列表中,然后使用itertools库中的permutations函数来生成所有可能的排列
import itertools
lst = []
for i in range(4):s = input()lst.append(s)
per = itertools.permutations(lst) # 生成一个包含所有排列情况的可迭代对象
ans = "".join(lst) # 拼接列表中的字符串
for i in per:ans = min(ans,"".join(i))
print(ans)
更好的解法
如果字符串数量增多,全排列的数量会大大增长导致我们无法枚举所有的可能。我们可以考虑直接找到最优的字符串。
我们假设字符串目前拼接顺序如下S1,a,b,S2 ,其中a,b 是单元字符串,而S1,S2则分别表示其他字符串拼接后的串。现在我们考虑交换a和b的位置能否使得整个字符串的字典序更小:
显而易见当a+b<b+a时,a在前时字典序更小,b+a<a+b 时交换a和b的位置能够使得最终的字符串字典序更小。 (此处的+ 表示字符串的拼接,> , < 表示字典序比较)
于是我们按照上述的比较规则对这个字符串数组进行排序,最终的顺序就是答案
from functools import cmp_to_key
lst = []
for i in range(4):s = input()lst.append(s)
def cmp(s1,s2): # 比较函数if(s1+s2 < s2+s1):return -1 # -1表示不需要交换位置elif(s1+s2 > s2+s1):return 1 # 1表示需要交换位置else :return 0
lst.sort(key = cmp_to_key(cmp))
print("".join(lst))
11.领取礼物
题意
【问题描述】
蓝桥村正在给村民们发放礼物。礼物通过一个礼物发放机完成。
村民们在机器前排着队领取礼物。
每个礼物有一个价值 v[i] ,有的高,有的低。每位村民有自己对于礼物的期望值 e[i] 。
礼物发放机每次会显示一个礼物,如果礼物的价值大于等于村民的期望值,村民就会高兴地把礼物拿走,并离开礼物发放机。如果礼物的价值比村民的期望值低,村民会让这个礼物取消,并让礼物发放机显示下一个礼物,并重新检查是否满足期望。村民会重复让礼物发放机显示下⼀个礼物,直到礼物发放机没有更多可以显示的礼物或礼物的价值大于等于自己的期望值。
如果礼物发放机中的所有礼物都显示完了,那么还没领到礼物的村民就无法领取礼物了。
如果所有的村民都领到了礼物,而礼物发放机还有礼物显示,村民们也不会再领取礼物。
现在,小蓝知道了每位村民的期望值,也知道了礼物发放机上礼物的显示顺序,请问总共有多少村民拿到了礼物?
【输入格式】
输入的第一行包含一个整数 n ,表示村民的个数。
第二行包含 n 个整数,相邻数之间使用一个空格分隔,依次表示排队的每位村民的期望值 e[i] 。
第三行包含一个整数 m ,表示礼物发放机会显示的礼物个数。
第四行包含 m 个整数,相邻数之间使用一个空格分隔,依次表示礼物发放机显示的礼物的价值 v[i] 。
【输出格式】
输出一行,包含一个整数,表示答案。
【样例输入】
6
6 5 5 3 6 0
9
9 9 8 2 4 4 3 5 3
【样例输出】
4
【样例说明】
前 4 位村民依次取到了第 1, 2, 3, 5 件礼物。后面的礼物未能满足第 5 位村民。
【评测用例规模与约定】
对于 30% 的评测用例,1 <= n, m <= 20 , 0 <= e[i], v[i] <= 100 。
对于 60% 的评测用例,1 <= n, m <= 300 , 0 <= e[i], v[i] <= 10000 。
对于所有评测用例,1 <= n, m <= 10000 , 0 <= e[i], v[i] <= 1000000 。
思路
模拟礼物分发的过程即可
使用for循环按顺序枚举每个村民,对于每个村民使用while循环来查找符合的礼物。
当所有村民都领到礼物,或者所有的礼物都分发完就结束循环
n = int(input())
villager = list(map(int,input().split()))
m = int(input())
gift = list(map(int,input().split()))
p = 0 # 现在分发到哪个礼物了
ans = 0
for x in villager:while(p < len(gift) and gift[p] < x):p += 1if(p == len(gift)):# 如果所有礼物都发完了breakans += 1 # 有合适的礼物给他p += 1
print(ans)
12. 十字矩阵
题意
【问题描述】
小蓝有一个 n 行 m 列的矩阵 a [ i ] [ j ] a[i][j] a[i][j],他想着矩阵中找出一个“十”字形状的区域,使得区域内的值的和最大。
一个“十”字形状的区域可以由两个行号 r 1 r1 r1 、 r 2 r2 r2 和两个列号 c 1 c1 c1 、 c 2 c2 c2 表示。“十”字的区域内包括第 r 1 r1 r1 行到 r 2 r2 r2 行的所有元素,以及第 c 1 c1 c1 列到 c 2 c2 c2 列的所有元素,既不在这几行也不在这几列的元素不在区域内。
为了保证是一个“十”字的形状,必须满足 1 < r 1 < = r 2 < n , 1 < c 1 < = c 2 < m 1 < r1 <= r2 < n,1 < c1 <= c2 < m 1<r1<=r2<n,1<c1<=c2<m。
【输入格式】
输入的第一行包含两个整数 $n, m $,分别表示行数和列数。
接下来 n n n 行,每行包含 m m m整数,相邻数之间使用一个空格分隔,依次表示矩阵的每行每列的值,本部分的第 i i i 行第 j j j 列表示 a [ i ] [ j ] a[i][j] a[i][j] 。
【输出格式】
输出一行包含一个整数,表示最大的和。
【样例输入】
5 6
1 -1 2 -2 3 -3
-1 2 -2 3 -3 4
2 -2 3 -3 4 -4
-2 3 -3 4 -4 5
3 -3 4 -4 5 -5
【样例输出】
14
【样例说明】
有两种方法可以得到最大的和。第一种是取 r 1 = 2 , r 2 = 4 , c 1 = 3 , c 2 = 5 r1=2, r2=4, c1=3, c2=5 r1=2,r2=4,c1=3,c2=5,第二种是取$ r1=2, r2=4, c1=5, c2=5 $。
【评测用例规模与约定】
对于 30% 的评测用例, 3 < = n , m < = 30 , − 1000 < = a [ i ] [ j ] < = 1000 3 <= n, m <= 30 ,-1000 <= a[i][j] <= 1000 3<=n,m<=30,−1000<=a[i][j]<=1000 。
对于 60% 的评测用例, 3 < = n , m < = 100 , − 1000 < = a [ i ] [ j ] < = 1000 3 <= n, m <= 100 ,-1000 <= a[i][j] <= 1000 3<=n,m<=100,−1000<=a[i][j]<=1000 。
对于所有评测用例,$3 <= n <= 100, 3 <= m <= 5000 ,-1000 <= a[i][j] <= 1000 $。
思路
部分分
本题难度明显高于其他题目,可以考虑拿部分分:
暴力枚举所有十字的可能情况,然后使用二维前缀和来计算这个十字中所有数的加和。时间复杂度( O ( n 2 m 2 ) O(n^2m^2) O(n2m2)
n,m = list(map(int,input().split()))
matrix = []
matrix.append([0] * (m+1))
# 让matrix的有效数据从下标1开始,便于进行前缀和计算
for i in range(n):lst = [0]lst = lst + list(map(int,input().split()))matrix.append(lst)
# 求二维前缀和
for i in range(1,n+1):for j in range(1,m+1):matrix[i][j] = matrix[i][j] + matrix[i-1][j] + matrix[i][j-1] - matrix[i-1][j-1]
ans = -1e9
for r1 in range(2,n): ## 枚举十字for r2 in range(r1,n):for c1 in range(2,m):for c2 in range(c1,m):## 计算十字的数字总和sm = 0sm += matrix[r2][m] - matrix[r1-1][m] # 十字的横sm += matrix[n][c2] - matrix[n][c1-1] # 十字的竖sm -= matrix[r2][c2] - matrix[r1-1][c2] - matrix[r2][c1-1] + matrix[r1-1][c1-1]# 减去重叠部分ans = max(ans,sm)
print(ans)
满分
观察满分的数据范围,发现n没有变大, 只有m变大了。
我们可以枚举 r 1 , r 2 r1,r2 r1,r2 的取值,当 r 1 , r 2 r1,r2 r1,r2 确定后, 本题就变为了“在一个一维数组中找和最大的子数组”问题。
这个子问题的复杂度是 O ( m ) O(m) O(m) 的,于是我们的总的复杂度就降到了 O ( n 2 m ) O(n^2m) O(n2m)
如何用 O ( n ) O(n) O(n)算法求解一维数组的最大子数组和?
例题:最大子数组和(leetcode)
对数组进行前缀和 s u m sum sum,那么子数组lst[l~r] 即 sum[r] - sum[l-1] ,显而易见当r确定后, 最小的 s u m [ l − 1 ] sum[l-1] sum[l−1] 能产生最大的 sum[r] - sum[l-1], 于是我们可以枚举右端点r, 左端点 l l l通过记录最小值得出。
n,m = list(map(int,input().split()))
matrix = []
matrix.append([0] * (m+1))
# 让matrix的有效数据从下标1开始,便于进行前缀和计算
for i in range(n):lst = [0]lst = lst + list(map(int,input().split()))matrix.append(lst)
pre = matrix.copy()
# 求二维前缀和
for i in range(1,n+1):for j in range(1,m+1):pre[i][j] = pre[i][j] + pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1]ans = -1e9
for r1 in range(2,n):for r2 in range(r1,n):x = pre[r2][m] - pre[r1-1][m] # 十字的横summ = [0] # 二维前缀和压缩到一维,并减去"横"for col in range(1,m+1):summ.append(pre[n][col] - (pre[r2][col] - pre[r1-1][col])minn = 0res = -1e9 # 子数组最大和for i in range(1,len(summ)):res = max(res,summ[i]-minn)minn = min(minn,summ[i])ans = max(ans,res + x)
print(ans)
相关文章:

第16届蓝桥杯模拟赛3 python组个人题解
第16届蓝桥杯模拟赛3 python组 思路和答案不保证正确 1.填空 如果一个数 p 是个质数,同时又是整数 a 的约数,则 p 称为 a 的一个质因数。 请问, 2024 的最大的质因数是多少? 因为是填空题,所以直接枚举2023~2 &am…...

企业知识管理战略整合新路径
跨部门知识协同机制 现代企业知识管理的核心挑战在于突破组织孤岛效应,跨部门知识协同机制的构建需依托结构化流程与智能化工具的融合。通过建立标准化知识元数据体系,企业可实现文档分类、版本控制及权限管理的统一规范,其中Baklib作为云端…...

GO 快速升级Go版本
由于底层依赖升级了,那我们也要跟着升,go老版本已经不足满足需求了,必须要将版本升级到1.22.0以上 查看当前Go版本 命令查看go版本 go version [rootlocalhost local]# go version go version go1.21.4 linux/amd64 [rootlocalhost local]# …...

RBAC授权
4 RBAC授权 4.1 什么是RBAC 在Kubernetes中,所有资源对象都是通过API进行操作,他们保存在etcd里。而对etcd的操作我们需要通过访问kube-apiserver来实现,上面的Service Account其实就是APIServer的认证过程,而授权的机制是通过RBA…...

搜广推校招面经三十一
vivo策略算法 一、机器学习中 L1 和 L2 正则化的原理 见【搜广推校招面经二十五】 L1 正则化将某些特征权重置0实现模型简化,而 L2 正则化主要通过平滑权重来实现模型简化。 1.1. 正则化的原理 正则化的核心思想是在损失函数中加入一个惩罚项(Regula…...

【JavaWeb13】了解ES6的核心特性,对于提高JavaScript编程效率有哪些潜在影响?
文章目录 🌍一. ES6 新特性❄️1. ES6 基本介绍❄️2. 基本使用2.1 let 声明变量2.2 const 声明常量/只读变量2.3 解构赋值2.4 模板字符串2.5 对象拓展运算符2.6 箭头函数 🌍二. Promise❄️1. 基本使用❄️2. 如何解决回调地狱问题2.1回调地狱问题2.2 使…...

C++知识整理day9——继承(基类与派生类之间的转换、派生类的默认成员函数、多继承问题)
文章目录 1.继承的概念和定义2.基类与派生类之间的转换3.继承中的作用域4.派生类的默认成员函数5.实现一个不能被继承的类6.继承与友元7.继承与静态成员8.多继承和菱形继承问题8.1 继承分类及菱形继承8.2 虚继承 1.继承的概念和定义 概念: 继承(inheritance)机制是⾯…...
函数)
pyautogui库的screenshot()函数
# 方法一 screenshot pyautogui.screenshot() screenshot.save("screenshot.png")# 方法二 # 获取屏幕分辨率 screen_width, screen_height pyautogui.size()# 截取桌面屏幕 screenshot pyautogui.screenshot(region(0, 0, screen_width, screen_height)) screens…...
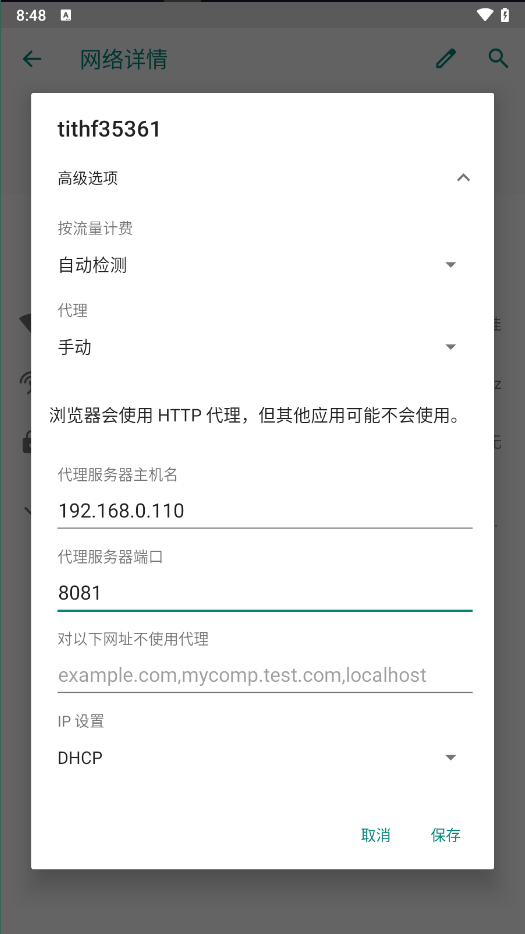
App测试--逍遥模拟器抓包问题
一、环境 逍遥模拟器、burp、adb、openssl(kali)。 二、配置 1.burp证书转换 下载证书 将burp证书复制进kali,使用kali的openssl(自带),执行以下命令。 openssl x509 -inform der -in cacert.der -out burp.pem openssl x509 -subject_hash_old -in…...

STM32 HAL库0.96寸OLED显示液晶屏
本文介绍了使用STM32 HAL库通过I2C协议驱动0.96寸OLED显示屏的方法。首先概述了OLED的基本特性和应用,然后详细讲解了汉字点阵生成的方法,并提供了完整的代码示例,包括初始化、清屏、字符串显示和自定义汉字显示函数。这些代码实现了在STM32F…...

动态表头导出EasyExcel
在 Spring Boot 中结合 EasyExcel 实现动态表头导出(无实体类,表头和字段(前端传表名,字段值动态查询,返回List<Map<String,Object>>)由前端传递)可以通过以下步骤实现。以下是完整…...

【前端】react+ts 轮播图的实现
一、场景描述 在很多网站的页面中都有轮播图,所以我想利用react.js和ts实现一个轮播图。自动轮播图已经在前面实现过了,如:https://blog.csdn.net/weixin_43872912/article/details/145622444?sharetypeblogdetail&sharerId145622444&a…...

清华大学出品DeepSeek 四部教程全收录(附下载包),清华deepseek文档下载地址
文章目录 前言一、清华大学deepseek教程(四部)二、清华大学deepseek教程全集1.清华大学第一版《DeepSeek:从入门到精通》2.清华大学第二版《DeepSeek赋能职场》3.清华大学第三版《普通人如何抓住DeepSeek红利》4.清华大学第四版:D…...

Android 布局系列(三):RelativeLayout 使用指南
引言 在 Android 开发中,布局管理是构建用户界面的核心。RelativeLayout 曾经是 Android 中非常流行的一种布局方式,广泛应用于各种项目中。它通过相对位置关系组织视图元素,使得我们可以根据父容器或者其他视图的位置来灵活调整子视图的布局…...

ubuntu20.04音频aplay调试
1、使用指定声卡,aplay 播放命令 aplay -D plughw:1,0 test2.wav2、 录音 arecord -Dhw:1,0 -d 10 -f cd -r 44100 -c 2 -t wav test.wav3、各个参数含义 -D 指定声卡编号 plughw:0,0 //0,0代表card0,device0,可以通过arecord -l获取 -f 录音格式 S16_LE…...

前缀和代码解析
前缀和是指数组一定范围的数的总和,常见的有两种,一维和二维,我会用两道题来分别解析 一维 DP34 【模板】前缀和 题目: 题目解析: 暴力解法 直接遍历数组,遍历到下标为 l 时,开始进行相加,直到遍历到下标为 r ,最后返回总和.这样做的时间复杂度为: O(n) public class Main …...
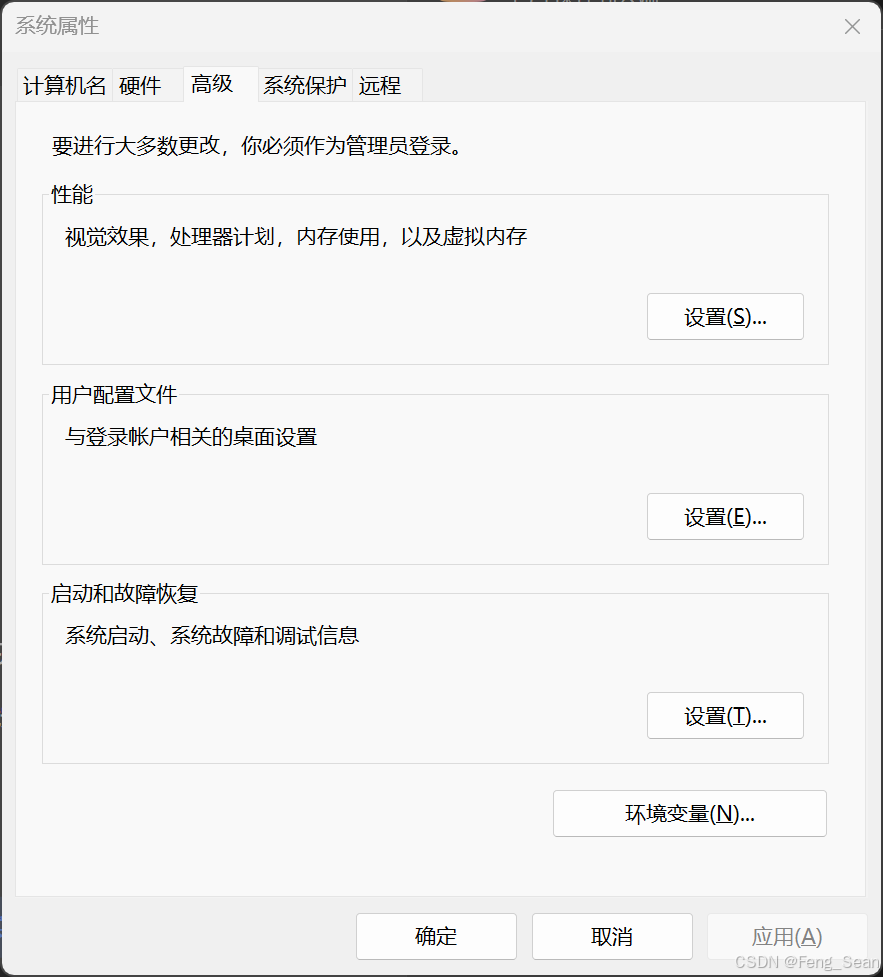
Windows 环境下安装 Anaconda 并配置
安装Anaconda 1. 下载安装包 官网下载:https://www.anaconda.com/download/success 也可以从国内镜像仓库下载: 中国科学技术大学 https://mirrors.ustc.edu.cn/ 清华大学开源软件镜像站 https://mirrors.tuna.tsinghua.edu.cn/ 2. 安装过程 双…...

大模型在尿潴留风险预测及围手术期方案制定中的应用研究
目录 一、引言 1.1 研究背景与意义 1.2 研究目的 1.3 研究方法与数据来源 二、大模型预测尿潴留的原理与方法 2.1 相关大模型介绍 2.2 模型构建与训练 2.3 模型评估指标与验证 三、术前尿潴留风险预测及方案制定 3.1 术前风险因素分析 3.2 大模型预测结果分析 3.3 …...

JavaScript 简单类型与复杂类型
在JavaScript中,根据数据存储的方式不同,变量可以分为两大类:简单类型(也称为基本数据类型或原始类型)和复杂类型(也称为引用数据类型)。理解这两者的区别对于编写高效且无误的代码至关重要。本…...

AI绘画软件Stable Diffusion详解教程(1):Windows系统本地化部署操作方法(专业版)
一、事前准备 1、一台配置不错的电脑,英伟达显卡,20系列起步,建议显存6G起步,安装win10或以上版本,我的显卡是40系列,16G显存,所以跑大部分的模型都比较快; 2、科学上网࿰…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
