python pickle模块
pickle 是 Python 的一个标准模块,它实现了基本的二进制协议,用于对象的序列化和反序列化。序列化是指将对象转换为字节流的过程,这样对象就可以被保存到文件中或通过网络传输。反序列化是指将字节流转换回对象的过程。
使用 pickle 序列化对象
要将一个对象序列化(即保存到文件中),你可以使用 pickle.dump() 函数。这个函数接受两个必需的参数:要序列化的对象和保存对象的文件对象(通常是一个打开的文件,模式为 'wb',表示写入二进制数据)。
import pickle# 创建一个要序列化的对象
data = {'name': 'Alice', 'age': 30, 'is_student': False}# 打开一个文件用于写入
with open('data.pkl', 'wb') as file:# 使用 pickle.dump() 将对象序列化并写入文件pickle.dump(data, file)
使用 pickle 反序列化对象
要从文件中反序列化(即读取并转换回对象)一个对象,你可以使用 pickle.load() 函数。这个函数接受一个必需的参数:一个包含序列化对象的文件对象(通常是一个打开的文件,模式为 'rb',表示读取二进制数据)。
import pickle# 打开一个包含序列化对象的文件用于读取
with open('data.pkl', 'rb') as file:# 使用 pickle.load() 从文件中读取并反序列化对象loaded_data = pickle.load(file)# 打印反序列化后的对象
print(loaded_data)
注意事项
-
安全性:
pickle序列化的数据可以被执行,因此从不受信任的来源加载数据可能是不安全的。恶意数据可以包含代码,当反序列化时会被执行。 -
兼容性:
pickle序列化的数据是与 Python 版本相关的。在不同版本的 Python 之间,序列化的数据可能不兼容。 -
性能:虽然
pickle对于简单的对象序列化来说通常足够快,但对于大型或复杂的数据结构,它可能不是最优的选择。 -
替代方案:对于需要跨语言或跨平台兼容性的场景,可能需要考虑使用其他序列化格式,如 JSON(使用
json模块)、XML、MessagePack 等。 -
高级用法:
pickle还提供了更高级的功能,如自定义对象的序列化行为(通过实现特殊方法如__getstate__()和__setstate__())、协议版本的选择(控制序列化的格式和兼容性)等。
总的来说,pickle 是一个强大且灵活的序列化工具,但在使用时需要注意安全性和兼容性等问题。
相关文章:

python pickle模块
pickle 是 Python 的一个标准模块,它实现了基本的二进制协议,用于对象的序列化和反序列化。序列化是指将对象转换为字节流的过程,这样对象就可以被保存到文件中或通过网络传输。反序列化是指将字节流转换回对象的过程。 使用 pickle 序列化对…...

第16届蓝桥杯模拟赛3 python组个人题解
第16届蓝桥杯模拟赛3 python组 思路和答案不保证正确 1.填空 如果一个数 p 是个质数,同时又是整数 a 的约数,则 p 称为 a 的一个质因数。 请问, 2024 的最大的质因数是多少? 因为是填空题,所以直接枚举2023~2 &am…...

企业知识管理战略整合新路径
跨部门知识协同机制 现代企业知识管理的核心挑战在于突破组织孤岛效应,跨部门知识协同机制的构建需依托结构化流程与智能化工具的融合。通过建立标准化知识元数据体系,企业可实现文档分类、版本控制及权限管理的统一规范,其中Baklib作为云端…...

GO 快速升级Go版本
由于底层依赖升级了,那我们也要跟着升,go老版本已经不足满足需求了,必须要将版本升级到1.22.0以上 查看当前Go版本 命令查看go版本 go version [rootlocalhost local]# go version go version go1.21.4 linux/amd64 [rootlocalhost local]# …...

RBAC授权
4 RBAC授权 4.1 什么是RBAC 在Kubernetes中,所有资源对象都是通过API进行操作,他们保存在etcd里。而对etcd的操作我们需要通过访问kube-apiserver来实现,上面的Service Account其实就是APIServer的认证过程,而授权的机制是通过RBA…...

搜广推校招面经三十一
vivo策略算法 一、机器学习中 L1 和 L2 正则化的原理 见【搜广推校招面经二十五】 L1 正则化将某些特征权重置0实现模型简化,而 L2 正则化主要通过平滑权重来实现模型简化。 1.1. 正则化的原理 正则化的核心思想是在损失函数中加入一个惩罚项(Regula…...

【JavaWeb13】了解ES6的核心特性,对于提高JavaScript编程效率有哪些潜在影响?
文章目录 🌍一. ES6 新特性❄️1. ES6 基本介绍❄️2. 基本使用2.1 let 声明变量2.2 const 声明常量/只读变量2.3 解构赋值2.4 模板字符串2.5 对象拓展运算符2.6 箭头函数 🌍二. Promise❄️1. 基本使用❄️2. 如何解决回调地狱问题2.1回调地狱问题2.2 使…...

C++知识整理day9——继承(基类与派生类之间的转换、派生类的默认成员函数、多继承问题)
文章目录 1.继承的概念和定义2.基类与派生类之间的转换3.继承中的作用域4.派生类的默认成员函数5.实现一个不能被继承的类6.继承与友元7.继承与静态成员8.多继承和菱形继承问题8.1 继承分类及菱形继承8.2 虚继承 1.继承的概念和定义 概念: 继承(inheritance)机制是⾯…...
函数)
pyautogui库的screenshot()函数
# 方法一 screenshot pyautogui.screenshot() screenshot.save("screenshot.png")# 方法二 # 获取屏幕分辨率 screen_width, screen_height pyautogui.size()# 截取桌面屏幕 screenshot pyautogui.screenshot(region(0, 0, screen_width, screen_height)) screens…...
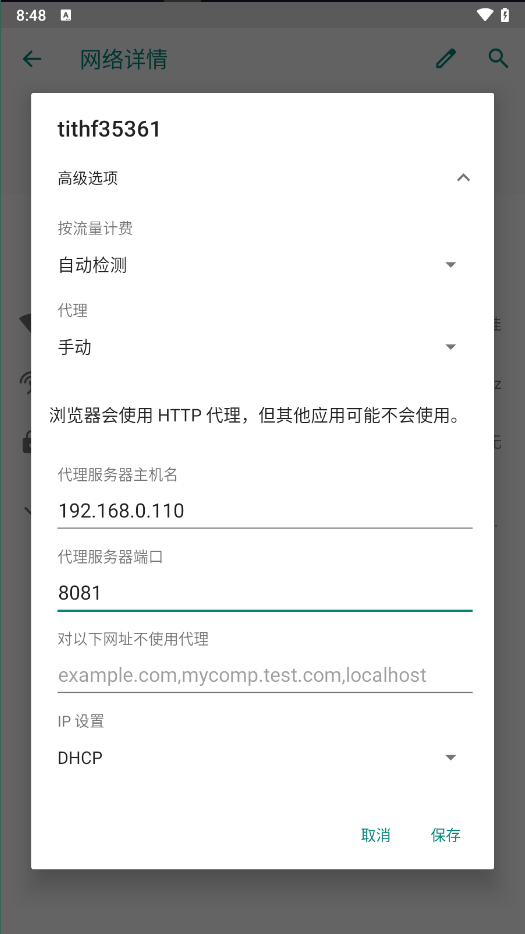
App测试--逍遥模拟器抓包问题
一、环境 逍遥模拟器、burp、adb、openssl(kali)。 二、配置 1.burp证书转换 下载证书 将burp证书复制进kali,使用kali的openssl(自带),执行以下命令。 openssl x509 -inform der -in cacert.der -out burp.pem openssl x509 -subject_hash_old -in…...

STM32 HAL库0.96寸OLED显示液晶屏
本文介绍了使用STM32 HAL库通过I2C协议驱动0.96寸OLED显示屏的方法。首先概述了OLED的基本特性和应用,然后详细讲解了汉字点阵生成的方法,并提供了完整的代码示例,包括初始化、清屏、字符串显示和自定义汉字显示函数。这些代码实现了在STM32F…...

动态表头导出EasyExcel
在 Spring Boot 中结合 EasyExcel 实现动态表头导出(无实体类,表头和字段(前端传表名,字段值动态查询,返回List<Map<String,Object>>)由前端传递)可以通过以下步骤实现。以下是完整…...

【前端】react+ts 轮播图的实现
一、场景描述 在很多网站的页面中都有轮播图,所以我想利用react.js和ts实现一个轮播图。自动轮播图已经在前面实现过了,如:https://blog.csdn.net/weixin_43872912/article/details/145622444?sharetypeblogdetail&sharerId145622444&a…...

清华大学出品DeepSeek 四部教程全收录(附下载包),清华deepseek文档下载地址
文章目录 前言一、清华大学deepseek教程(四部)二、清华大学deepseek教程全集1.清华大学第一版《DeepSeek:从入门到精通》2.清华大学第二版《DeepSeek赋能职场》3.清华大学第三版《普通人如何抓住DeepSeek红利》4.清华大学第四版:D…...

Android 布局系列(三):RelativeLayout 使用指南
引言 在 Android 开发中,布局管理是构建用户界面的核心。RelativeLayout 曾经是 Android 中非常流行的一种布局方式,广泛应用于各种项目中。它通过相对位置关系组织视图元素,使得我们可以根据父容器或者其他视图的位置来灵活调整子视图的布局…...

ubuntu20.04音频aplay调试
1、使用指定声卡,aplay 播放命令 aplay -D plughw:1,0 test2.wav2、 录音 arecord -Dhw:1,0 -d 10 -f cd -r 44100 -c 2 -t wav test.wav3、各个参数含义 -D 指定声卡编号 plughw:0,0 //0,0代表card0,device0,可以通过arecord -l获取 -f 录音格式 S16_LE…...

前缀和代码解析
前缀和是指数组一定范围的数的总和,常见的有两种,一维和二维,我会用两道题来分别解析 一维 DP34 【模板】前缀和 题目: 题目解析: 暴力解法 直接遍历数组,遍历到下标为 l 时,开始进行相加,直到遍历到下标为 r ,最后返回总和.这样做的时间复杂度为: O(n) public class Main …...
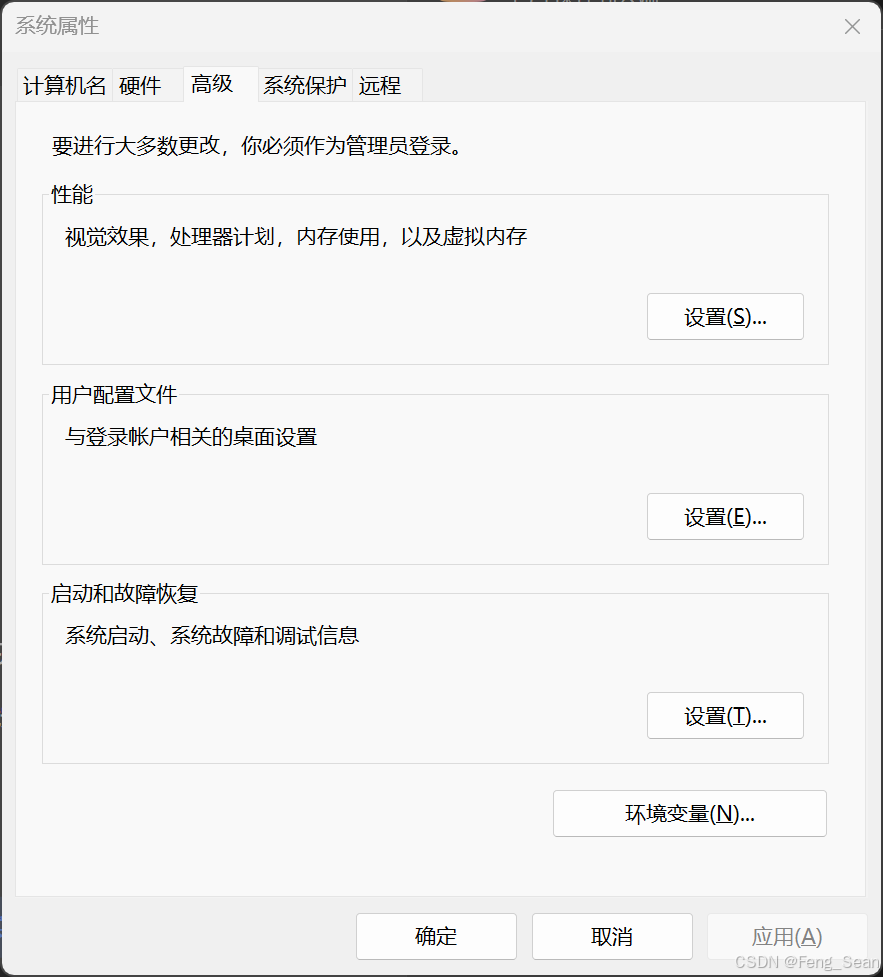
Windows 环境下安装 Anaconda 并配置
安装Anaconda 1. 下载安装包 官网下载:https://www.anaconda.com/download/success 也可以从国内镜像仓库下载: 中国科学技术大学 https://mirrors.ustc.edu.cn/ 清华大学开源软件镜像站 https://mirrors.tuna.tsinghua.edu.cn/ 2. 安装过程 双…...

大模型在尿潴留风险预测及围手术期方案制定中的应用研究
目录 一、引言 1.1 研究背景与意义 1.2 研究目的 1.3 研究方法与数据来源 二、大模型预测尿潴留的原理与方法 2.1 相关大模型介绍 2.2 模型构建与训练 2.3 模型评估指标与验证 三、术前尿潴留风险预测及方案制定 3.1 术前风险因素分析 3.2 大模型预测结果分析 3.3 …...

JavaScript 简单类型与复杂类型
在JavaScript中,根据数据存储的方式不同,变量可以分为两大类:简单类型(也称为基本数据类型或原始类型)和复杂类型(也称为引用数据类型)。理解这两者的区别对于编写高效且无误的代码至关重要。本…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
