Fisher信息矩阵(Fisher Information Matrix,简称FIM)
Fisher信息矩阵简介
Fisher信息矩阵(Fisher Information Matrix,简称FIM)是统计学和信息理论中的一个重要概念,广泛应用于参数估计、统计推断和机器学习领域。它以统计学家罗纳德·费希尔(Ronald Fisher)的名字命名,反映了概率分布对参数变化的敏感度,是衡量模型参数估计不确定性的核心工具。
什么是Fisher信息矩阵?
Fisher信息矩阵是一个对称的方阵,用于描述概率密度函数(或概率质量函数)在其参数下的信息含量。简单来说,它告诉我们通过观测数据能够获得多少关于未知参数的信息。对于一个参数化的概率分布 ( p ( x ∣ θ ) p(x|\theta) p(x∣θ) ),其中 ( θ \theta θ ) 是参数向量,Fisher信息矩阵 ( I ( θ ) I(\theta) I(θ) ) 的定义基于对数似然函数的二阶导数。
数学定义
假设我们有一个概率密度函数 ( p ( x ∣ θ ) p(x|\theta) p(x∣θ) ),其中 ( θ = ( θ 1 , θ 2 , … , θ k ) \theta = (\theta_1, \theta_2, \dots, \theta_k) θ=(θ1,θ2,…,θk) ) 是 ( k k k ) 维参数向量。Fisher信息矩阵 ( I ( θ ) I(\theta) I(θ) ) 的元素可以通过以下两种等价的方式定义:
-
基于期望的定义:
I ( θ ) i j = E [ ∂ log p ( x ∣ θ ) ∂ θ i ∂ log p ( x ∣ θ ) ∂ θ j ∣ θ ] I(\theta)_{ij} = E\left[ \frac{\partial \log p(x|\theta)}{\partial \theta_i} \frac{\partial \log p(x|\theta)}{\partial \theta_j} \bigg| \theta \right] I(θ)ij=E[∂θi∂logp(x∣θ)∂θj∂logp(x∣θ) θ]
这里,( E [ ⋅ ] E[\cdot] E[⋅] ) 表示在给定 ( θ \theta θ ) 下的期望,( ∂ log p ( x ∣ θ ) ∂ θ i \frac{\partial \log p(x|\theta)}{\partial \theta_i} ∂θi∂logp(x∣θ) ) 是对数似然函数对第 ( i i i ) 个参数的偏导数,也称为得分函数(score function)。 -
基于二阶导数的定义(在一定条件下等价):
I ( θ ) i j = − E [ ∂ 2 log p ( x ∣ θ ) ∂ θ i ∂ θ j ∣ θ ] I(\theta)_{ij} = -E\left[ \frac{\partial^2 \log p(x|\theta)}{\partial \theta_i \partial \theta_j} \bigg| \theta \right] I(θ)ij=−E[∂θi∂θj∂2logp(x∣θ) θ]
这是对数似然函数的二阶偏导数的负期望值,通常称为Hessian矩阵的期望。
这两种定义在正则条件下(例如,分布满足可微性和期望的可交换性)是等价的。
一个简单例子
为了更好地理解,假设我们有一个正态分布 ( N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2) ),其中参数 ( θ = ( μ , σ 2 ) \theta = (\mu, \sigma^2) θ=(μ,σ2) )。我们来计算它的Fisher信息矩阵:
对数似然函数
对于单个观测值 ( x x x ):
log p ( x ∣ μ , σ 2 ) = − 1 2 log ( 2 π σ 2 ) − ( x − μ ) 2 2 σ 2 \log p(x|\mu, \sigma^2) = -\frac{1}{2} \log (2\pi \sigma^2) - \frac{(x - \mu)^2}{2\sigma^2} logp(x∣μ,σ2)=−21log(2πσ2)−2σ2(x−μ)2
计算得分函数
- 对 ( μ \mu μ ) 求偏导:
∂ log p ∂ μ = x − μ σ 2 \frac{\partial \log p}{\partial \mu} = \frac{x - \mu}{\sigma^2} ∂μ∂logp=σ2x−μ - 对 ( σ 2 \sigma^2 σ2 ) 求偏导:
∂ log p ∂ σ 2 = − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 \frac{\partial \log p}{\partial \sigma^2} = -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} ∂σ2∂logp=−2σ21+2(σ2)2(x−μ)2
Fisher信息矩阵元素
- ( I 11 = E [ ( x − μ σ 2 ) 2 ] = 1 σ 2 I_{11} = E\left[ \left( \frac{x - \mu}{\sigma^2} \right)^2 \right] = \frac{1}{\sigma^2} I11=E[(σ2x−μ)2]=σ21 ),因为 ( E [ ( x − μ ) 2 ] = σ 2 E[(x - \mu)^2] = \sigma^2 E[(x−μ)2]=σ2 )。
- ( I 22 = E [ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) 2 ] = 1 2 ( σ 2 ) 2 I_{22} = E\left[ \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right)^2 \right] = \frac{1}{2(\sigma^2)^2} I22=E[(−2σ21+2(σ2)2(x−μ)2)2]=2(σ2)21 )。计算过程见下文。
- ( I 12 = I 21 = E [ x − μ σ 2 ⋅ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) ] = 0 I_{12} = I_{21} = E\left[ \frac{x - \mu}{\sigma^2} \cdot \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right) \right] = 0 I12=I21=E[σ2x−μ⋅(−2σ21+2(σ2)2(x−μ)2)]=0 )(交叉项期望为零)。计算过程见下文。
于是,Fisher信息矩阵为:
I ( θ ) = [ 1 σ 2 0 0 1 2 ( σ 2 ) 2 ] I(\theta) = \begin{bmatrix} \frac{1}{\sigma^2} & 0 \\ 0 & \frac{1}{2(\sigma^2)^2} \end{bmatrix} I(θ)=[σ21002(σ2)21]
Fisher信息矩阵的性质
- 正定性:如果模型是可识别的(即不同参数对应不同分布),Fisher信息矩阵通常是正定的,这意味着它可以用来衡量参数估计的“曲率”。
- 对角元素:对角线上的元素 ( I i i I_{ii} Iii ) 表示单个参数 ( θ i \theta_i θi ) 的信息量。
- 独立性:如果参数之间是独立的(得分函数的交叉项期望为零),矩阵将是对角矩阵。
应用
-
Cramér-Rao下界:
Fisher信息矩阵的一个重要应用是提供参数估计方差的下界。对于一个无偏估计器 ( θ ^ \hat{\theta} θ^ ),其协方差矩阵满足:
Cov ( θ ^ ) ≥ I ( θ ) − 1 \text{Cov}(\hat{\theta}) \geq I(\theta)^{-1} Cov(θ^)≥I(θ)−1
其中 ( I ( θ ) − 1 I(\theta)^{-1} I(θ)−1 ) 是Fisher信息矩阵的逆矩阵。这表明,估计器的精度受限于Fisher信息。 -
最大似然估计:
在最大似然估计(MLE)中,Fisher信息矩阵的逆可以用来近似估计参数的协方差矩阵,尤其是在大样本情况下。 -
机器学习:
在深度学习中,Fisher信息矩阵被用于优化算法(如自然梯度下降)和模型正则化,帮助理解损失函数的几何结构。
总结
Fisher信息矩阵是统计学中的一个强大工具,它连接了概率分布、参数估计和信息理论。通过量化数据中包含的参数信息,它为我们提供了理解模型行为和估计精度的基础。尽管计算复杂,但在许多实际问题中,它可以通过数值方法或近似来实现。
如果你需要更深入的探讨或具体例子,请告诉我,我可以进一步扩展!
I 22 I_{22} I22复杂计算过程
以下是关于Fisher信息矩阵元素 ( I 22 I_{22} I22 ) 的计算过程
第一部分:计算 ( I 22 I_{22} I22 )
给出的表达式是:
I 22 = E [ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) 2 ] I_{22} = E\left[ \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right)^2 \right] I22=E[(−2σ21+2(σ2)2(x−μ)2)2]
并提到它等于 ( 1 2 ( σ 2 ) 2 \frac{1}{2(\sigma^2)^2} 2(σ2)21 )。让我们一步步验证这个计算过程,假设 ( x ∼ N ( μ , σ 2 ) x \sim N(\mu, \sigma^2) x∼N(μ,σ2) ),因为Fisher信息矩阵通常在正态分布的背景下计算。
步骤 1:定义对数似然函数
对于来自正态分布 ( N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2) ) 的单个观测值 ( x x x ),概率密度函数为:
p ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) p(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right) p(x∣μ,σ2)=2πσ21exp(−2σ2(x−μ)2)
对数似然函数为:
log p ( x ∣ μ , σ 2 ) = − 1 2 log ( 2 π σ 2 ) − ( x − μ ) 2 2 σ 2 \log p(x | \mu, \sigma^2) = -\frac{1}{2} \log (2\pi \sigma^2) - \frac{(x - \mu)^2}{2\sigma^2} logp(x∣μ,σ2)=−21log(2πσ2)−2σ2(x−μ)2
步骤 2:对 ( σ 2 \sigma^2 σ2 ) 求偏导数
由于 ( I 22 I_{22} I22 ) 对应参数 ( θ 2 = σ 2 \theta_2 = \sigma^2 θ2=σ2 ),我们需要计算:
∂ log p ∂ σ 2 \frac{\partial \log p}{\partial \sigma^2} ∂σ2∂logp
- 第一项:( − 1 2 log ( 2 π σ 2 ) = − 1 2 log 2 π − 1 2 log σ 2 -\frac{1}{2} \log (2\pi \sigma^2) = -\frac{1}{2} \log 2\pi - \frac{1}{2} \log \sigma^2 −21log(2πσ2)=−21log2π−21logσ2 )
∂ ∂ σ 2 ( − 1 2 log σ 2 ) = − 1 2 ⋅ 1 σ 2 = − 1 2 σ 2 \frac{\partial}{\partial \sigma^2} \left( -\frac{1}{2} \log \sigma^2 \right) = -\frac{1}{2} \cdot \frac{1}{\sigma^2} = -\frac{1}{2\sigma^2} ∂σ2∂(−21logσ2)=−21⋅σ21=−2σ21
(这里使用了链式法则:( d d σ 2 log σ 2 = 1 σ 2 \frac{d}{d\sigma^2} \log \sigma^2 = \frac{1}{\sigma^2} dσ2dlogσ2=σ21 )。)
- 第二项:( − ( x − μ ) 2 2 σ 2 -\frac{(x - \mu)^2}{2\sigma^2} −2σ2(x−μ)2 )
∂ ∂ σ 2 ( − ( x − μ ) 2 2 σ 2 ) = − ( x − μ ) 2 2 ⋅ ( − 1 ) ( σ 2 ) − 2 = ( x − μ ) 2 2 ( σ 2 ) 2 \frac{\partial}{\partial \sigma^2} \left( -\frac{(x - \mu)^2}{2\sigma^2} \right) = -\frac{(x - \mu)^2}{2} \cdot (-1) (\sigma^2)^{-2} = \frac{(x - \mu)^2}{2(\sigma^2)^2} ∂σ2∂(−2σ2(x−μ)2)=−2(x−μ)2⋅(−1)(σ2)−2=2(σ2)2(x−μ)2
因此:
∂ log p ∂ σ 2 = − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 \frac{\partial \log p}{\partial \sigma^2} = -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} ∂σ2∂logp=−2σ21+2(σ2)2(x−μ)2
这与给出的期望内的表达式一致.
步骤 3:对偏导数平方
I 22 = E [ ( ∂ log p ∂ σ 2 ) 2 ] = E [ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) 2 ] I_{22} = E\left[ \left( \frac{\partial \log p}{\partial \sigma^2} \right)^2 \right] = E\left[ \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right)^2 \right] I22=E[(∂σ2∂logp)2]=E[(−2σ21+2(σ2)2(x−μ)2)2]
展开平方:
( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) 2 = ( − 1 2 σ 2 ) 2 + 2 ( − 1 2 σ 2 ) ( ( x − μ ) 2 2 ( σ 2 ) 2 ) + ( ( x − μ ) 2 2 ( σ 2 ) 2 ) 2 \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right)^2 = \left( -\frac{1}{2\sigma^2} \right)^2 + 2 \left( -\frac{1}{2\sigma^2} \right) \left( \frac{(x - \mu)^2}{2(\sigma^2)^2} \right) + \left( \frac{(x - \mu)^2}{2(\sigma^2)^2} \right)^2 (−2σ21+2(σ2)2(x−μ)2)2=(−2σ21)2+2(−2σ21)(2(σ2)2(x−μ)2)+(2(σ2)2(x−μ)2)2
逐项简化:
-
( ( − 1 2 σ 2 ) 2 = 1 4 ( σ 2 ) 2 \left( -\frac{1}{2\sigma^2} \right)^2 = \frac{1}{4(\sigma^2)^2} (−2σ21)2=4(σ2)21 )
-
( 2 ( − 1 2 σ 2 ) ( ( x − μ ) 2 2 ( σ 2 ) 2 ) = − ( x − μ ) 2 2 ( σ 2 ) 3 2 \left( -\frac{1}{2\sigma^2} \right) \left( \frac{(x - \mu)^2}{2(\sigma^2)^2} \right) = -\frac{(x - \mu)^2}{2(\sigma^2)^3} 2(−2σ21)(2(σ2)2(x−μ)2)=−2(σ2)3(x−μ)2 )
-
( ( ( x − μ ) 2 2 ( σ 2 ) 2 ) 2 = ( x − μ ) 4 4 ( σ 2 ) 4 \left( \frac{(x - \mu)^2}{2(\sigma^2)^2} \right)^2 = \frac{(x - \mu)^4}{4(\sigma^2)^4} (2(σ2)2(x−μ)2)2=4(σ2)4(x−μ)4 )
因此:
I 22 = E [ 1 4 ( σ 2 ) 2 − ( x − μ ) 2 2 ( σ 2 ) 3 + ( x − μ ) 4 4 ( σ 2 ) 4 ] I_{22} = E\left[ \frac{1}{4(\sigma^2)^2} - \frac{(x - \mu)^2}{2(\sigma^2)^3} + \frac{(x - \mu)^4}{4(\sigma^2)^4} \right] I22=E[4(σ2)21−2(σ2)3(x−μ)2+4(σ2)4(x−μ)4]
步骤 4:计算期望
由于 ( σ 2 \sigma^2 σ2 ) 是参数(常数),我们对 ( x x x ) 取期望:
-
( E [ 1 4 ( σ 2 ) 2 ] = 1 4 ( σ 2 ) 2 E\left[ \frac{1}{4(\sigma^2)^2} \right] = \frac{1}{4(\sigma^2)^2} E[4(σ2)21]=4(σ2)21 ) (常数)
-
( E [ − ( x − μ ) 2 2 ( σ 2 ) 3 ] = − 1 2 ( σ 2 ) 3 E [ ( x − μ ) 2 ] E\left[ -\frac{(x - \mu)^2}{2(\sigma^2)^3} \right] = -\frac{1}{2(\sigma^2)^3} E[(x - \mu)^2] E[−2(σ2)3(x−μ)2]=−2(σ2)31E[(x−μ)2] )
-
( E [ ( x − μ ) 4 4 ( σ 2 ) 4 ] = 1 4 ( σ 2 ) 4 E [ ( x − μ ) 4 ] E\left[ \frac{(x - \mu)^4}{4(\sigma^2)^4} \right] = \frac{1}{4(\sigma^2)^4} E[(x - \mu)^4] E[4(σ2)4(x−μ)4]=4(σ2)41E[(x−μ)4] )
对于 ( x ∼ N ( μ , σ 2 ) x \sim N(\mu, \sigma^2) x∼N(μ,σ2) ):
-
( E [ ( x − μ ) 2 ] = 方差 = σ 2 E[(x - \mu)^2] = \text{方差} = \sigma^2 E[(x−μ)2]=方差=σ2 )
-
( E [ ( x − μ ) 4 ] = 3 ( σ 2 ) 2 E[(x - \mu)^4] = 3(\sigma^2)^2 E[(x−μ)4]=3(σ2)2 ) (正态分布的四阶中心矩)
代入:
I 22 = 1 4 ( σ 2 ) 2 − 1 2 ( σ 2 ) 3 ⋅ σ 2 + 1 4 ( σ 2 ) 4 ⋅ 3 ( σ 2 ) 2 I_{22} = \frac{1}{4(\sigma^2)^2} - \frac{1}{2(\sigma^2)^3} \cdot \sigma^2 + \frac{1}{4(\sigma^2)^4} \cdot 3(\sigma^2)^2 I22=4(σ2)21−2(σ2)31⋅σ2+4(σ2)41⋅3(σ2)2
= 1 4 ( σ 2 ) 2 − 1 2 ( σ 2 ) 2 + 3 4 ( σ 2 ) 2 = \frac{1}{4(\sigma^2)^2} - \frac{1}{2(\sigma^2)^2} + \frac{3}{4(\sigma^2)^2} =4(σ2)21−2(σ2)21+4(σ2)23
= ( 1 4 − 2 4 + 3 4 ) 1 ( σ 2 ) 2 = 2 4 1 ( σ 2 ) 2 = 1 2 ( σ 2 ) 2 = \left( \frac{1}{4} - \frac{2}{4} + \frac{3}{4} \right) \frac{1}{(\sigma^2)^2} = \frac{2}{4} \frac{1}{(\sigma^2)^2} = \frac{1}{2(\sigma^2)^2} =(41−42+43)(σ2)21=42(σ2)21=2(σ2)21
这证实了:
I 22 = 1 2 ( σ 2 ) 2 I_{22} = \frac{1}{2(\sigma^2)^2} I22=2(σ2)21
这个计算依赖于对偏导数平方后展开,并利用正态分布的矩,结果如上所示。
第二部分:两个偏导的乘积是否等价于平方?
两个偏导的乘积等价成平方了吗?让我们在 ( θ = ( μ , σ 2 ) \theta = (\mu, \sigma^2) θ=(μ,σ2) ) 的Fisher信息矩阵背景下解释这个问题。
Fisher信息矩阵元素
-
( I 11 = E [ ( ∂ log p ∂ μ ) 2 ] I_{11} = E\left[ \left( \frac{\partial \log p}{\partial \mu} \right)^2 \right] I11=E[(∂μ∂logp)2] )
-
( I 12 = I 21 = E [ ∂ log p ∂ μ ∂ log p ∂ σ 2 ] I_{12} = I_{21} = E\left[ \frac{\partial \log p}{\partial \mu} \frac{\partial \log p}{\partial \sigma^2} \right] I12=I21=E[∂μ∂logp∂σ2∂logp] )
-
( I 22 = E [ ( ∂ log p ∂ σ 2 ) 2 ] I_{22} = E\left[ \left( \frac{\partial \log p}{\partial \sigma^2} \right)^2 \right] I22=E[(∂σ2∂logp)2] ) (如上计算)
对角元素是平方,非对角元素是乘积。
解答交叉项期望为零
为什么 ( I 12 = I 21 = E [ x − μ σ 2 ⋅ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) ] = 0 I_{12} = I_{21} = E\left[ \frac{x - \mu}{\sigma^2} \cdot \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right) \right] = 0 I12=I21=E[σ2x−μ⋅(−2σ21+2(σ2)2(x−μ)2)]=0 )?
背景
在Fisher信息矩阵中,( I i j I_{ij} Iij ) 表示参数 ( θ i \theta_i θi ) 和 ( θ j \theta_j θj ) 的信息关联。对于正态分布 ( N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2) ),我们令 ( θ 1 = μ \theta_1 = \mu θ1=μ ),( θ 2 = σ 2 \theta_2 = \sigma^2 θ2=σ2 )。这里,( I 12 I_{12} I12 ) 是交叉项,定义为:
I 12 = E [ ∂ log p ∂ μ ⋅ ∂ log p ∂ σ 2 ] I_{12} = E\left[ \frac{\partial \log p}{\partial \mu} \cdot \frac{\partial \log p}{\partial \sigma^2} \right] I12=E[∂μ∂logp⋅∂σ2∂logp]
它衡量了 ( μ \mu μ ) 和 ( σ 2 \sigma^2 σ2 ) 之间的信息相关性。如果 ( I 12 = 0 I_{12} = 0 I12=0 ),说明这两个参数在信息上是“正交”的,也就是说,一个参数的得分函数(score function)与另一个参数的得分函数在期望上是无关的。
计算过程
步骤 1:计算交叉项 ( I 12 I_{12} I12 )
I 12 = E [ ∂ log p ∂ μ ⋅ ∂ log p ∂ σ 2 ] = E [ x − μ σ 2 ⋅ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) ] I_{12} = E\left[ \frac{\partial \log p}{\partial \mu} \cdot \frac{\partial \log p}{\partial \sigma^2} \right] = E\left[ \frac{x - \mu}{\sigma^2} \cdot \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right) \right] I12=E[∂μ∂logp⋅∂σ2∂logp]=E[σ2x−μ⋅(−2σ21+2(σ2)2(x−μ)2)]
展开乘积:
x − μ σ 2 ⋅ ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 ) = x − μ σ 2 ⋅ ( − 1 2 σ 2 ) + x − μ σ 2 ⋅ ( x − μ ) 2 2 ( σ 2 ) 2 \frac{x - \mu}{\sigma^2} \cdot \left( -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} \right) = \frac{x - \mu}{\sigma^2} \cdot \left( -\frac{1}{2\sigma^2} \right) + \frac{x - \mu}{\sigma^2} \cdot \frac{(x - \mu)^2}{2(\sigma^2)^2} σ2x−μ⋅(−2σ21+2(σ2)2(x−μ)2)=σ2x−μ⋅(−2σ21)+σ2x−μ⋅2(σ2)2(x−μ)2
= − x − μ 2 ( σ 2 ) 2 + ( x − μ ) 3 2 ( σ 2 ) 3 = -\frac{x - \mu}{2(\sigma^2)^2} + \frac{(x - \mu)^3}{2(\sigma^2)^3} =−2(σ2)2x−μ+2(σ2)3(x−μ)3
因此:
I 12 = E [ − x − μ 2 ( σ 2 ) 2 + ( x − μ ) 3 2 ( σ 2 ) 3 ] I_{12} = E\left[ -\frac{x - \mu}{2(\sigma^2)^2} + \frac{(x - \mu)^3}{2(\sigma^2)^3} \right] I12=E[−2(σ2)2x−μ+2(σ2)3(x−μ)3]
由于期望是线性的,我们可以分开计算:
I 12 = − 1 2 ( σ 2 ) 2 E [ x − μ ] + 1 2 ( σ 2 ) 3 E [ ( x − μ ) 3 ] I_{12} = -\frac{1}{2(\sigma^2)^2} E[x - \mu] + \frac{1}{2(\sigma^2)^3} E[(x - \mu)^3] I12=−2(σ2)21E[x−μ]+2(σ2)31E[(x−μ)3]
步骤 2:计算正态分布的矩
对于 ( x ∼ N ( μ , σ 2 ) x \sim N(\mu, \sigma^2) x∼N(μ,σ2) ):
-
( E [ x − μ ] = 0 E[x - \mu] = 0 E[x−μ]=0 ) (一阶中心矩,因为均值为 ( μ \mu μ ))
-
( E [ ( x − μ ) 3 ] = 0 E[(x - \mu)^3] = 0 E[(x−μ)3]=0 ) (三阶中心矩,由于正态分布是对称的,奇数阶中心矩为零)
代入:
I 12 = − 1 2 ( σ 2 ) 2 ⋅ 0 + 1 2 ( σ 2 ) 3 ⋅ 0 = 0 I_{12} = -\frac{1}{2(\sigma^2)^2} \cdot 0 + \frac{1}{2(\sigma^2)^3} \cdot 0 = 0 I12=−2(σ2)21⋅0+2(σ2)31⋅0=0
所以:
I 12 = 0 I_{12} = 0 I12=0
这就是为什么交叉项期望为零。
解释:为什么会是零?
这个结果的背后有深刻的统计意义:
-
正态分布的对称性:
- ( x − μ x - \mu x−μ ) 的分布是对称的(服从 ( N ( 0 , σ 2 ) N(0, \sigma^2) N(0,σ2) )),其奇数阶中心矩(如 ( E [ x − μ ] E[x - \mu] E[x−μ] ) 和 ( E [ ( x − μ ) 3 ] E[(x - \mu)^3] E[(x−μ)3] ))都为零。
- ( ∂ log p ∂ μ = x − μ σ 2 \frac{\partial \log p}{\partial \mu} = \frac{x - \mu}{\sigma^2} ∂μ∂logp=σ2x−μ ) 是线性项,期望为零。
- ( ∂ log p ∂ σ 2 = − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 \frac{\partial \log p}{\partial \sigma^2} = -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} ∂σ2∂logp=−2σ21+2(σ2)2(x−μ)2 ) 包含常数项和二次项,乘以奇数项 ( x − μ x - \mu x−μ ) 后,奇数阶的部分在期望下消失。
-
参数的正交性:
- 在正态分布中,( μ \mu μ ) 和 ( σ 2 \sigma^2 σ2 ) 的得分函数是“正交”的,意味着它们提供的信息在统计上是独立的。
- 当 ( I 12 = 0 I_{12} = 0 I12=0 ),Fisher信息矩阵是对角矩阵,表明 ( μ \mu μ ) 和 ( σ 2 \sigma^2 σ2 ) 的估计不会相互干扰。
-
直观理解:
- ( x − μ σ 2 \frac{x - \mu}{\sigma^2} σ2x−μ ) 表示数据偏离均值的程度,是随机的正负波动。
- ( − 1 2 σ 2 + ( x − μ ) 2 2 ( σ 2 ) 2 -\frac{1}{2\sigma^2} + \frac{(x - \mu)^2}{2(\sigma^2)^2} −2σ21+2(σ2)2(x−μ)2 ) 与方差相关,是关于偏差大小的量。
- 这两者乘积的正负波动在对称分布下互相抵消,期望为零。
验证:另一种方法(二阶导数)
Fisher信息矩阵也可以用二阶导数的负期望定义:
I 12 = − E [ ∂ 2 log p ∂ μ ∂ σ 2 ] I_{12} = -E\left[ \frac{\partial^2 \log p}{\partial \mu \partial \sigma^2} \right] I12=−E[∂μ∂σ2∂2logp]
计算二阶混合偏导:
∂ ∂ σ 2 ( x − μ σ 2 ) = ( x − μ ) ⋅ ( − 1 ) ( σ 2 ) − 2 = − x − μ ( σ 2 ) 2 \frac{\partial}{\partial \sigma^2} \left( \frac{x - \mu}{\sigma^2} \right) = (x - \mu) \cdot (-1) (\sigma^2)^{-2} = -\frac{x - \mu}{(\sigma^2)^2} ∂σ2∂(σ2x−μ)=(x−μ)⋅(−1)(σ2)−2=−(σ2)2x−μ
I 12 = − E [ − x − μ ( σ 2 ) 2 ] = 1 ( σ 2 ) 2 E [ x − μ ] = 0 I_{12} = -E\left[ -\frac{x - \mu}{(\sigma^2)^2} \right] = \frac{1}{(\sigma^2)^2} E[x - \mu] = 0 I12=−E[−(σ2)2x−μ]=(σ2)21E[x−μ]=0
这与得分函数方法一致,进一步确认 ( I 12 = 0 I_{12} = 0 I12=0 )。
结论
( I 12 = 0 I_{12} = 0 I12=0 ) 是因为正态分布的奇数阶中心矩为零,导致 ( ∂ log p ∂ μ \frac{\partial \log p}{\partial \mu} ∂μ∂logp ) 和 ( ∂ log p ∂ σ 2 \frac{\partial \log p}{\partial \sigma^2} ∂σ2∂logp ) 的乘积在期望下抵消。这反映了 ( μ \mu μ ) 和 ( σ 2 \sigma^2 σ2 ) 在信息上的独立性,是正态分布的一个重要特性。
后记
2025年2月24日21点43分于上海,在Grok3大模型辅助下完成。
相关文章:
)
Fisher信息矩阵(Fisher Information Matrix,简称FIM)
Fisher信息矩阵简介 Fisher信息矩阵(Fisher Information Matrix,简称FIM)是统计学和信息理论中的一个重要概念,广泛应用于参数估计、统计推断和机器学习领域。它以统计学家罗纳德费希尔(Ronald Fisher)的名…...

Vue2+Three.js加载并展示一个三维模型(提供Gitee源码)
目录 一、案例截图 二、安装Three.js 三、代码实现 四、Gitee源码 一、案例截图 二、安装Three.js npm install three 三、代码实现 模型资源我是放在public文件夹下面的: 完整代码: <template><div><div ref"container&qu…...

Linux红帽:RHCSA认证知识讲解(三)Linux基础指令与Vim编辑器的使用
Linux红帽:RHCSA认证知识讲解(三)Linux基础指令与Vim编辑器的使用 前言一、Linux基础指令二、Linux 文件系统层次结构概念三、通过路径指定文件四、使用命令行工具管理文件五、Vim 的安装方式六、Vim 的操作模式七、红帽建议掌握的 Vim 键和命…...

python读取sqlite温度数据,并画出折线图
需求: 在Windows下请用python画出折线图,x轴是时间,y轴是温度temperature 和体感温度feels_like_temperature 。可以选择县市近1小时,近1天,近1个月的。sqlite文件weather_data.db当前目录下,建表结构如下…...

《论企业集成平台的理解与应用》审题技巧 - 系统架构设计师
企业集成平台的理解与应用——论文写作框架 一、考点概述 本论题“企业集成平台的理解与应用”主要考察的是计算机软件测试工程师对于企业集成平台(EIP)的深入理解以及在实际项目中的应用能力。论题涵盖了以下几个核心内容: 首先ÿ…...

UE Python笔记
插件 官方 商城 Python Editorhttps://www.fab.com/listings/f4c99ba0-1a86-4f6a-b19d-2fd13f15961b GitHUB 好像只更新到了2020年4.2x的版本。可能有大佬改了5.x的版本。也希望分享给我一份。谢谢 https://github.com/20tab/UnrealEnginePython 学习笔记 网上教程一大堆。…...

使用django调用deepseek api,搭建ai网站
一、deepseek简介 DeepSeek是一家人工智能公司,专注于开发先进的人工智能模型和技术。以下是关于DeepSeek的一些详细介绍: 1.公司背景 DeepSeek由杭州深度求索人工智能基础技术研究有限公司开发,致力于通过创新的技术和算法,推…...

YOLOv12 ——基于卷积神经网络的快速推理速度与注意力机制带来的增强性能结合
概述 实时目标检测对于许多实际应用来说已经变得至关重要,而Ultralytics公司开发的YOLO(You Only Look Once,只看一次)系列一直是最先进的模型系列,在速度和准确性之间提供了稳健的平衡。注意力机制的低效阻碍了它们在…...

两台互通的服务器使用Docker部署一主两从MySQL8.0.35
文章目录 1. 使用Docker Overlay网络(需Swarm模式)在服务器1(172.25.0.19)上:在服务器2(172.25.0.20)上:创建 overlay 网络(172.25.0.19): 2. 部署…...

Java23种设计模式案例
目录 一、概述 二、创建型模式 (Creational Patterns) 单例模式 (Singleton Pattern) 工厂方法模式 (Factory Method Pattern) 抽象工厂模式 (Abstract Factory Pattern) 建造者模式 (Builder Pattern) 原型模式 (Prototype Pattern) 三、结构型模式 (Structu…...
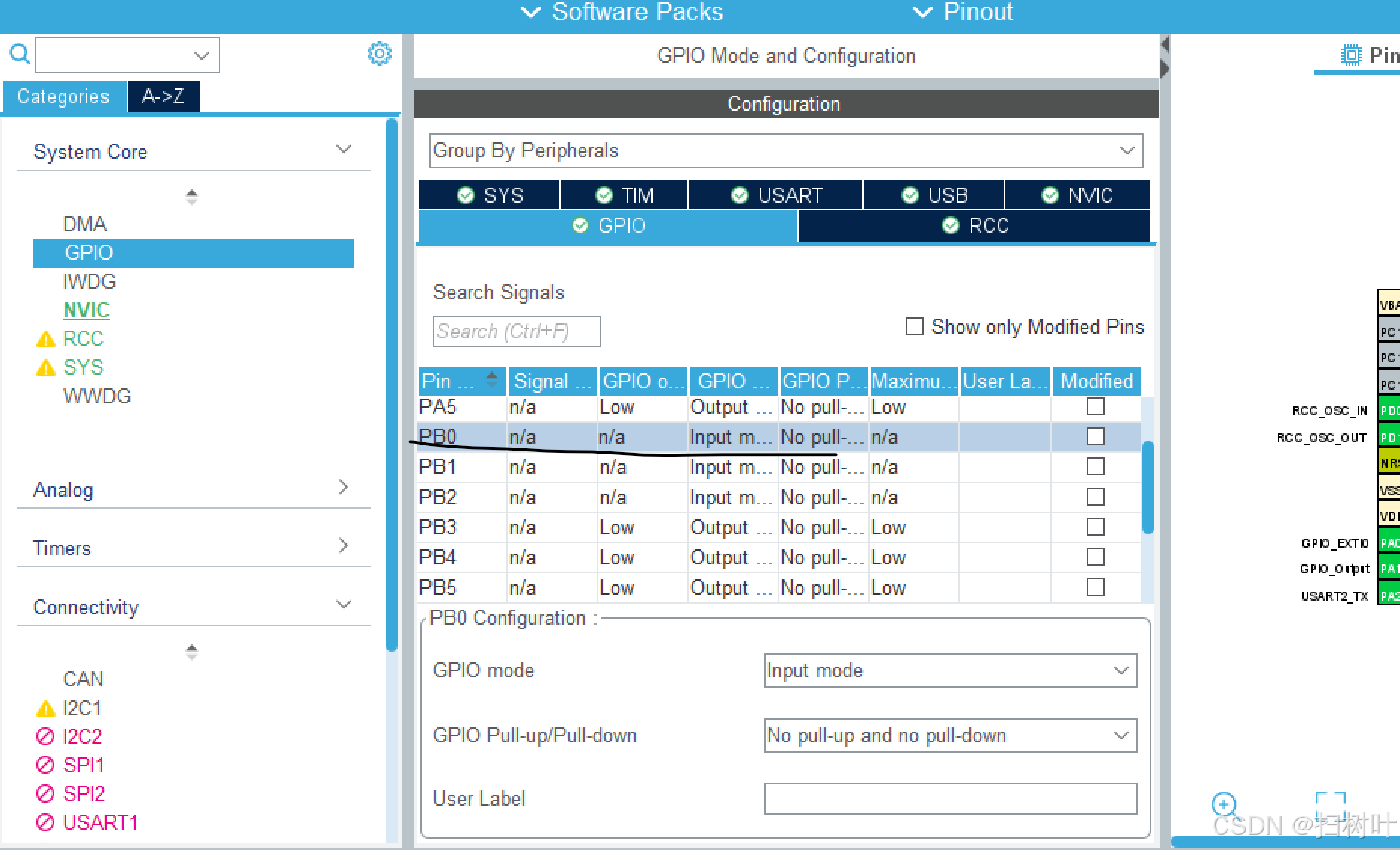
stm32hal库寻迹+蓝牙智能车(STM32F103C8T6)
简介: 这个小车的芯片是STM32F103C8T6,其他的芯片也可以照猫画虎,基本配置差不多,要注意的就是,管脚复用,管脚的特殊功能,(这点不用担心,hal库每个管脚的功能都会给你罗列,很方便的.)由于我做的比较简单,只是用到了几个简单外设.主要是由带霍尔编码器电机的车模,电机…...

JavaScript知识点4
1.解释一下这段JavaScript代码 var fruits ["Apple", "Orange", "Apple", "Mango"]; var a fruits.indexOf("Apple",-1); console.log("index"a); 输出的a值为-1,indexOf的第二个参数是-1…...

形式化数学编程在AI医疗中的探索路径分析
一、引言 1.1 研究背景与意义 在数字化时代,形式化数学编程和 AI 形式化医疗作为前沿领域,正逐渐改变着我们的生活和医疗模式。形式化数学编程是一种运用数学逻辑和严格的形式化语言来描述和验证程序的技术,它通过数学的精确性和逻辑性,确保程序的正确性和可靠性。在软件…...

QT 引入Quazip和Zlib源码工程到项目中,无需编译成库,跨平台,加密压缩,带有压缩进度
前言 最近在做项目时遇到一个需求,需要将升级的文件压缩成zip,再进行传输; 通过网络调研,有许多方式可以实现,例如QT私有模块的ZipReader、QZipWriter;或者第三方库zlib或者libzip或者quazip等࿱…...

Ubuntu 安装 Nginx并配置反向代理
Ubuntu版本:Ubuntu 24.04.2 LTS 一、安装Nginx 更新系统软件包 安装前需确保系统处于最新状态,避免依赖冲突 sudo apt update && sudo apt upgrade -y 安装Nginx主程序 Ubuntu官方仓库已包含稳定版Nginx,直接安装即可 sudo…...

GitHub SSH连接问题解决指南
🔍 GitHub SSH连接问题解决指南 问题描述 遇到错误:ssh: connect to host github.com port 22: Connection refused 说明您的网络环境无法访问GitHub的SSH端口22,常见原因: 防火墙/网络运营商限制(国内常见…...
 获取当前线程ID实现)
C++ 跨平台的 GetCurrentThreadId() 获取当前线程ID实现
支持:C11 及早前标准库版本,而无需使用:std::this_thread::get_id()。 支持:NDK/ANDROID、Windows、Linux、MacOS X 等多个操作系统平台。 int64_t GetCurrentThreadId() noexcept { #if defined(_WIN32) || defined(_WIN64)retu…...

钉钉MAKE AI生态大会思考
1. 核心特性 1.1 底层模型开放 除原有模型通义千问外,新接入猎户星空、智普、MinMax、月之暗面、百川智能、零一万物。 1.2 AI搜索 AI搜索贯通企业和个人散落在各地的知识(聊天记录、文档、会议、日程、知识库、项目等),通过大模型对知识逻辑化,直接生成搜索的答案,并…...
SQL笔记#复杂查询
一、视图 1、视图和表 使用试图时会执行SELECT语句并创建一张临时表。视图中保存的是SELECT语句;表中保存的是实际数据。 2、创建视图的方法 CREATE VIEW 视图名称(<视图列名1>,<视图列名2>,……) AS <SELECT语句> CREATE VIEW ProductSum (prod…...

【Linux】基于UDP/TCP套接字编程与守护进程
目录 一、网路套接字编程 (一)基础概念 1、源IP地址与目的IP地址 2、端口号 3、TCP与UDP 4、网络字节序 (二)套接字编程接口 1、socket 常见API 2、sockaddr结构 (三)UDP套接字 1、UDP服务器创建…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
