穷举vs暴搜vs深搜vs回溯vs剪枝(典型算法思想)—— OJ例题算法解析思路

回溯算法的模版
void backtrack(vector<int>& path, vector<int>& choice, ...)
{// 满⾜结束条件if (/* 满⾜结束条件 */) {// 将路径添加到结果集中res.push_back(path);return;}// 遍历所有选择for (int i = 0; i < choices.size(); i++) {// 做出选择path.push_back(choices[i]);// 做出当前选择后继续搜索backtrack(path, choices);// 撤销选择path.pop_back();}
}



目录
回溯算法的模版
一、46. 全排列 - 力扣(LeetCode)
算法代码:
1. 类的成员变量
2. permute 函数
3. dfs 函数
4. 回溯的核心思想
5. 代码的优化空间
6. 代码的复杂度分析
7. 代码的改进版本
总结
二、78. 子集 - 力扣(LeetCode)
递归流程:
解法一:算法代码(剪枝->回溯->递归出口)
1. 类的成员变量
2. subsets 函数
3. dfs 函数
4. 回溯的核心思想
5. 代码的优化空间
6. 代码的复杂度分析
7. 代码的改进版本(避免重复子集)
改进点:
8. 总结
解法二:算法代码(回溯->剪枝->递归出口)
1. 类的成员变量
2. subsets 函数
3. dfs 函数
4. 代码的核心思想
5. 代码的优化空间
6. 代码的复杂度分析
7. 代码的改进版本(避免重复子集)
改进点:
8. 总结
一、46. 全排列 - 力扣(LeetCode)

算法代码:
class Solution {vector<vector<int>> ret;vector<int> path;bool check[7];public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums) {if (path.size() == nums.size()) {ret.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (!check[i]) {path.push_back(nums[i]);check[i] = true;dfs(nums);// 回溯 -> 恢复现场path.pop_back();check[i] = false;}}}
};
1. 类的成员变量
-
ret:用于存储所有可能的排列结果,类型为vector<vector<int>>。 -
path:用于存储当前正在构建的排列,类型为vector<int>。 -
check:用于标记某个元素是否已经被使用过,类型为bool数组,大小为 7(假设输入数组的长度不超过 7)。
2. permute 函数
-
这是主函数,接收一个整数数组
nums作为输入,并返回所有可能的排列。 -
调用
dfs(nums)开始深度优先搜索。 -
最终返回
ret,即所有排列的结果。
3. dfs 函数
-
这是递归函数,用于生成所有可能的排列。
-
递归终止条件:如果
path的大小等于nums的大小,说明当前path已经是一个完整的排列,将其加入到ret中,并返回。 -
递归过程:
-
遍历
nums数组中的每一个元素。 -
如果当前元素没有被使用过(
check[i] == false),则将其加入到path中,并标记为已使用。 -
递归调用
dfs,继续生成下一个位置的元素。 -
回溯:在递归返回后,撤销当前的选择(即从
path中移除最后一个元素,并将check[i]重新标记为未使用),以便尝试其他可能的排列。
-
4. 回溯的核心思想
-
回溯是一种通过递归来尝试所有可能的选择,并在每一步撤销选择以回到上一步的算法。
-
在这段代码中,回溯体现在
path.pop_back()和check[i] = false这两行代码上。它们的作用是撤销当前的选择,以便尝试其他可能的排列。
5. 代码的优化空间
-
check数组的大小是固定的 7,这意味着如果nums的大小超过 7,代码将无法正确处理。可以将check数组的大小动态设置为nums.size()。 -
可以使用
std::swap来直接在原数组上进行排列,从而减少path和check的使用,进一步优化空间复杂度。
6. 代码的复杂度分析
-
时间复杂度:O(n!),其中 n 是
nums的大小。因为全排列的数量是 n!。 -
空间复杂度:O(n!),用于存储所有排列的结果。递归栈的深度为 n,因此递归的空间复杂度为 O(n)。
7. 代码的改进版本
class Solution {vector<vector<int>> ret;public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int start) {if (start == nums.size()) {ret.push_back(nums);return;}for (int i = start; i < nums.size(); i++) {swap(nums[start], nums[i]);dfs(nums, start + 1);swap(nums[start], nums[i]); // 回溯}}
};在这个改进版本中,我们直接在原数组上进行排列,减少了 path 和 check 的使用,从而优化了空间复杂度。
总结

这段代码通过深度优先搜索和回溯的思想,实现了全排列的生成。代码的核心在于递归和回溯的处理,通过撤销选择来尝试所有可能的排列。
二、78. 子集 - 力扣(LeetCode)

递归流程:


解法一:算法代码(剪枝->回溯->递归出口)
// 解法⼀:
class Solution {vector<vector<int>> ret;vector<int> path;public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos) {if (pos == nums.size()) {ret.push_back(path);return;}// 选path.push_back(nums[pos]);dfs(nums, pos + 1);path.pop_back(); // 恢复现场// 不选dfs(nums, pos + 1);}
};
1. 类的成员变量
-
ret:用于存储所有子集的结果,类型为vector<vector<int>>。 -
path:用于存储当前正在构建的子集,类型为vector<int>。
2. subsets 函数
-
这是主函数,接收一个整数数组
nums作为输入,并返回所有可能的子集。 -
调用
dfs(nums, 0)开始深度优先搜索,0表示从数组的第一个元素开始处理。 -
最终返回
ret,即所有子集的结果。
3. dfs 函数
-
这是递归函数,用于生成所有可能的子集。
-
递归终止条件:如果
pos等于nums的大小,说明已经处理完所有元素,此时path中存储的就是一个子集,将其加入到ret中,并返回。 -
递归过程:
-
选择当前元素:
-
将
nums[pos]加入到path中。 -
递归调用
dfs(nums, pos + 1),继续处理下一个元素。 -
在递归返回后,撤销选择(即从
path中移除最后一个元素),以便尝试不选择当前元素的情况。
-
-
不选择当前元素:
-
直接递归调用
dfs(nums, pos + 1),跳过当前元素,继续处理下一个元素。
-
-
4. 回溯的核心思想
-
回溯是一种通过递归来尝试所有可能的选择,并在每一步撤销选择以回到上一步的算法。
-
在这段代码中,回溯体现在
path.pop_back()这一行代码上。它的作用是撤销当前的选择,以便尝试不选择当前元素的情况。
5. 代码的优化空间
-
如果输入数组
nums中包含重复元素,这段代码会生成重复的子集。可以通过排序和剪枝来避免重复子集的生成。 -
可以将
path改为引用传递,减少拷贝的开销。
6. 代码的复杂度分析
-
时间复杂度:O(2^n),其中 n 是
nums的大小。因为每个元素有两种选择(选或不选),总共有 2^n 个子集。 -
空间复杂度:O(n),递归栈的深度为 n。结果存储空间不计入空间复杂度。
7. 代码的改进版本(避免重复子集)
如果输入数组 nums 中包含重复元素,可以通过排序和剪枝来避免生成重复的子集。改进后的代码如下:
class Solution {vector<vector<int>> ret;vector<int> path;public:vector<vector<int>> subsets(vector<int>& nums) {sort(nums.begin(), nums.end()); // 排序,便于剪枝dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos) {ret.push_back(path); // 每次递归都加入当前子集for (int i = pos; i < nums.size(); i++) {if (i > pos && nums[i] == nums[i - 1]) continue; // 剪枝,避免重复path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back(); // 回溯}}
};改进点:
-
排序:先对
nums排序,使得相同的元素相邻。 -
剪枝:在递归过程中,如果当前元素和前一个元素相同,并且不是第一次遇到该元素,则跳过,避免重复子集。
-
提前加入子集:在每次递归开始时,直接将当前
path加入到ret中,这样可以避免在递归终止时才加入子集。
8. 总结
这段代码通过深度优先搜索和回溯的思想,实现了求解数组的所有子集。代码的核心在于对每个元素的选择和不选择两种情况的分支处理,并通过回溯撤销选择以尝试其他可能性。如果输入数组包含重复元素,可以通过排序和剪枝来优化,避免生成重复子集。
解法二:算法代码(回溯->剪枝->递归出口)
// 解法⼆:
class Solution {vector<vector<int>> ret;vector<int> path;public:vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos) {ret.push_back(path);for (int i = pos; i < nums.size(); i++) {path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back(); // 恢复现场}}
};
1. 类的成员变量
-
ret:用于存储所有子集的结果,类型为vector<vector<int>>。 -
path:用于存储当前正在构建的子集,类型为vector<int>。
2. subsets 函数
-
这是主函数,接收一个整数数组
nums作为输入,并返回所有可能的子集。 -
调用
dfs(nums, 0)开始深度优先搜索,0表示从数组的第一个元素开始处理。 -
最终返回
ret,即所有子集的结果。
3. dfs 函数
-
这是递归函数,用于生成所有可能的子集。
-
递归过程:
-
将当前子集加入结果:
-
在每次递归调用开始时,直接将当前
path加入到ret中。这是因为path在每一层递归中都表示一个有效的子集。
-
-
遍历数组元素:
-
从当前位置
pos开始遍历nums数组。 -
将当前元素
nums[i]加入到path中,表示选择该元素。 -
递归调用
dfs(nums, i + 1),继续处理下一个元素。 -
在递归返回后,撤销选择(即从
path中移除最后一个元素),以便尝试其他可能的子集。
-
-
4. 代码的核心思想
-
子集的生成:
-
子集的生成可以看作是对每个元素的选择或不选择。
-
通过递归和回溯,代码枚举了所有可能的选择组合。
-
-
提前加入子集:
-
在每次递归调用开始时,直接将当前
path加入到ret中。这是因为path在每一层递归中都表示一个有效的子集,无需等到递归终止才加入。
-
5. 代码的优化空间
-
如果输入数组
nums中包含重复元素,这段代码会生成重复的子集。可以通过排序和剪枝来避免重复子集的生成。 -
可以将
path改为引用传递,减少拷贝的开销。
6. 代码的复杂度分析
-
时间复杂度:O(2^n),其中 n 是
nums的大小。因为每个元素有两种选择(选或不选),总共有 2^n 个子集。 -
空间复杂度:O(n),递归栈的深度为 n。结果存储空间不计入空间复杂度。
7. 代码的改进版本(避免重复子集)
如果输入数组 nums 中包含重复元素,可以通过排序和剪枝来避免生成重复的子集。改进后的代码如下:
class Solution {vector<vector<int>> ret;vector<int> path;public:vector<vector<int>> subsets(vector<int>& nums) {sort(nums.begin(), nums.end()); // 排序,便于剪枝dfs(nums, 0);return ret;}void dfs(vector<int>& nums, int pos) {ret.push_back(path); // 将当前子集加入结果for (int i = pos; i < nums.size(); i++) {if (i > pos && nums[i] == nums[i - 1]) continue; // 剪枝,避免重复path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back(); // 回溯}}
};改进点:
-
排序:先对
nums排序,使得相同的元素相邻。 -
剪枝:在递归过程中,如果当前元素和前一个元素相同,并且不是第一次遇到该元素,则跳过,避免重复子集。
8. 总结
这段代码通过深度优先搜索和回溯的思想,实现了求解数组的所有子集。与解法一相比,解法二的代码更加简洁,直接通过循环和递归来生成所有子集。如果输入数组包含重复元素,可以通过排序和剪枝来优化,避免生成重复子集。代码的核心思想是对每个元素的选择和不选择进行枚举,并通过回溯撤销选择以尝试其他可能性。
重点:
递归的本质
递归是一种通过函数调用自身来解决问题的编程技巧。在递归过程中,问题的规模会逐渐减小,直到达到一个终止条件。递归的核心思想是分治,即将一个大问题分解为若干个小问题,然后分别解决这些小问题。
在子集问题中,递归的作用是对每个元素做出决策(选或不选),从而生成所有可能的子集。
为什么解法一不需要 for 循环?
在解法一中,递归的逻辑是对每个元素做出“选”或“不选”的决策。具体来说:
-
对于当前元素
nums[pos],有两种选择:-
选择它:将其加入
path,然后递归处理下一个元素(pos + 1)。 -
不选择它:直接递归处理下一个元素(
pos + 1)。
-
-
递归的终止条件是
pos == nums.size(),表示已经处理完所有元素。
这种递归逻辑已经隐含了对所有元素的遍历,因此不需要显式的 for 循环。
为什么解法二需要 for 循环?
在解法二中,递归的逻辑是显式地遍历数组中的元素,依次生成子集。具体来说:
-
for循环从pos开始遍历数组nums,表示从当前位置开始选择元素。 -
对于每个元素
nums[i],将其加入path,然后递归处理下一个元素(i + 1)。 -
在递归返回后,通过
path.pop_back()回溯,恢复现场,尝试下一个元素。
这种递归逻辑通过 for 循环显式地遍历元素,确保每个元素都有机会被选中,并且避免生成重复的子集。
递归和 for 循环的关系
-
递归的本质是遍历:递归确实可以遍历所有元素,但遍历的方式可以是隐式的(如解法一)或显式的(如解法二)。
-
是否需要
for循环:取决于递归的逻辑设计。如果递归的逻辑已经隐含了对所有元素的遍历(如解法一),则不需要for循环;如果需要显式地遍历元素(如解法二),则需要for循环。
两种解法的对比
| 特性 | 解法一(无 for 循环) | 解法二(有 for 循环) |
|---|---|---|
| 递归逻辑 | 对每个元素做出“选”或“不选”的决策 | 显式遍历元素,生成子集 |
是否需要 for 循环 | 否 | 是 |
| 代码结构 | 更简洁 | 更直观 |
| 时间复杂度 | O(2^n) | O(2^n) |
为什么解法二需要 for 循环?
解法二的递归逻辑是通过 for 循环显式地遍历元素,确保每个元素都有机会被选中,并且避免生成重复的子集。具体来说:
-
显式遍历元素:
for循环从pos开始遍历数组nums,表示从当前位置开始选择元素。 -
避免重复子集:通过
for循环从pos开始遍历,可以避免生成重复的子集。例如,如果已经选择了nums[1],那么后续的子集只能从nums[2]开始选择,而不能回头选择nums[0]。 -
生成所有子集:通过
for循环和递归的结合,确保所有可能的子集都被生成。
总结
-
递归确实可以遍历所有元素,但遍历的方式可以是隐式的(如解法一)或显式的(如解法二)。
-
是否需要
for循环取决于递归的逻辑设计。如果递归的逻辑已经隐含了对所有元素的遍历,则不需要for循环;如果需要显式地遍历元素,则需要for循环。 -
解法一和解法二都是正确的,只是它们的递归逻辑和实现方式不同。解法一更简洁,解法二更直观。
相关文章:

穷举vs暴搜vs深搜vs回溯vs剪枝(典型算法思想)—— OJ例题算法解析思路
回溯算法的模版 void backtrack(vector<int>& path, vector<int>& choice, ...) {// 满⾜结束条件if (/* 满⾜结束条件 */) {// 将路径添加到结果集中res.push_back(path);return;}// 遍历所有选择for (int i 0; i < choices.size(); i) {// 做出选择…...

在ubuntu 24.04.2 通过 Kubeadm 安装 Kubernetes v1.31.6
文章目录 1. 简介2. 准备3. 配置 containerd4. kubeadm 安装集群5. 安装网络 calico 插件 1. 简介 本指南介绍了如何在 Ubuntu 24.04.2 LTS 上安装和配置 Kubernetes 1.31.6 集群,包括容器运行时 containerd 的安装与配置,以及使用 kubeadm 进行集群初始…...

基于Python socket库构建的基于 P2P 的文件共享系统示例
基于 P2P 的文件共享系统 实现方式: 使用 Python 的socket库构建 P2P 网络,节点之间通过 TCP 或 UDP 协议进行通信。每个节点维护一个文件列表,并向其他节点广播自己拥有的文件信息。当一个节点需要某个文件时,它会向网络中的其…...

JavaScript 函数重载:灵活应对多场景的编程技巧
在 JavaScript 中,函数重载(Function Overloading)是一个常见的需求。尽管 JavaScript 本身并不支持传统意义上的函数重载(即在同一个作用域内定义多个同名函数,根据参数的不同调用不同的函数),…...

通过 PromptTemplate 生成干净的 SQL 查询语句并执行SQL查询语句
问题描述 在使用 LangChain 和 Llama 模型生成 SQL 查询时,遇到了 sqlite3.OperationalError 错误。错误信息如下: OperationalError: (sqlite3.OperationalError) near "sql SELECT Name FROM MediaType LIMIT 5; ": syntax error [SQL: …...

用大白话解释缓存Redis +MongoDB是什么有什么用怎么用
Redis和MongoDB是什么? Redis:像你家的“小冰箱”,专门存高频使用的食物(数据)。它是基于内存的键值数据库,读写速度极快(每秒超10万次操作)。比如你每次打开手机App,用…...

计算机毕业设计SpringBoot+Vue.js汽车销售网站(源码+文档+PPT+讲解)
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...

【0010】HTML水平线标签详解
如果你觉得我的文章写的不错,请关注我哟,请点赞、评论,收藏此文章,谢谢! 本文内容体系结构如下: 一、水平线标签概述 在HTML中,<hr>标签用于在网页上插入一条水平线,其主要…...

FastExcel与Reactor响应式编程深度集成技术解析
一、技术融合背景与核心价值 在2025年企业级应用开发中,大规模异步Excel处理与响应式系统架构的结合已成为技术刚需。FastExcel与Reactor的整合方案,通过以下技术协同实现突破性性能: 内存效率革命:FastExcel的流式字节操作与Re…...

Netty是如何实现零拷贝的?
大家好,我是锋哥。今天分享关于【Netty是如何实现零拷贝的?】面试题。希望对大家有帮助; Netty是如何实现零拷贝的? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 Netty是一个高性能的Java网络应用框架,它…...

【大模型➕知识图谱】大模型结合医疗知识图谱:解锁智能辅助诊疗系统新范式
【大模型➕知识图谱】大模型结合医疗知识图谱:解锁智能辅助诊疗系统新范式 大模型结合医疗知识图谱:解锁智能辅助诊疗系统新范式引言一、系统架构1.1 系统架构图1.2 架构模块说明1.2.1 用户输入1.2.2 大模型(语义理解与意图识别)1.2.3 Agent(问题解析与任务分配)1.2.4 问…...

Spring Boot @Component注解介绍
Component 是 Spring 中的一个核心注解,用于声明一个类为 Spring 管理的组件(Bean)。它是一个通用的注解,可以用于任何层次的类(如服务层、控制器层、持久层等)。通过 Component 注解,Spring 会…...
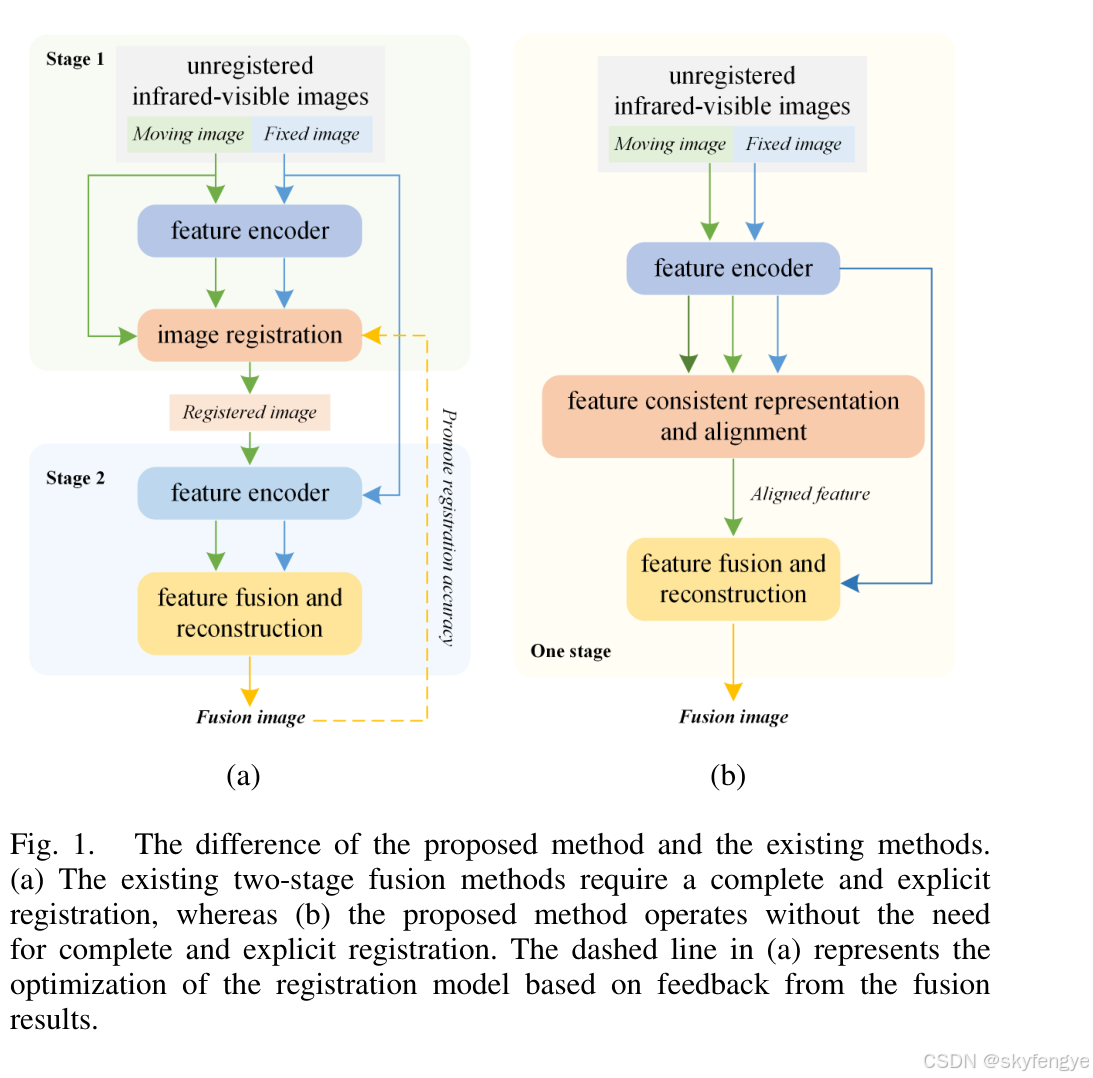
MulFS-CAP: Multimodal Fusion-supervisedCross-modal
一种用于无注册红外-可见图像融合的单阶段框架。与传统的两阶段方法不同,MulFS-CAP结合了隐式注册和融合,简化了处理流程并增强了实用性。该方法使用共享的浅层特征编码器,同时进行特征对齐和图像融合。通过引入可学习的模态字典,…...

WordPress多语言插件GTranslate
GTranslate是一个免费的WordPress多语言插件,它允许您将网站内容翻译成多种语言。这个插件提供了一个简单易用的界面,让您可以在WordPress后台直接进行翻译操作。以下是GTranslate插件的一些主要特点: 免费使用:GTranslate插件完…...

wordpress子分类调用父分类名称和链接的3种方法
专为导航而生,在wordpress模板制作过程中常常会在做breadcrumbs导航时会用到,子分类调用父分类的名称和链接,下面这段简洁的代码,可以完美解决这个问题。 <?php echo get_category_parents( $cat, true, » ); ?…...

Prometheus + Grafana 监控
Prometheus Grafana 监控 官网介绍:Prometheus 是一个开源系统 监控和警报工具包最初由 SoundCloud 构建。自 2012 年成立以来,许多 公司和组织已经采用了 Prometheus,并且该项目具有非常 活跃的开发人员和用户社区。它现在是一个独立的开源…...

初学STM32之简单认识IO口配置(学习笔记)
在使用51单片机的时候基本上不需要额外的配置IO,不过在使用特定的IO的时候需要额外的设计外围电路,比如PO口它是没有内置上拉电阻的。因此若想P0输出高电平,它就需要外接上拉电平。(当然这不是说它输入不需要上拉电阻,…...

springboot2.7.18升级springboot3.3.0遇到的坑
druid的警告,警告如下: 运行警告2025-02-28T09:20:31.28508:00 WARN 18800 --- [ restartedMain] trationDelegate$BeanPostProcessorChecker : Bean com.alibaba.druid.spring.boot3.autoconfigure.stat.DruidSpringAopConfiguration of type [com.a…...

gtest 和 gmock讲解
Google Test(gtest)和 Google Mock(gmock)是 Google 开发的用于 C 的测试框架和模拟框架,以下是对它们的详细讲解: Google Test(gtest) 简介 Google Test 是一个用于 C 的单元测试框…...

GC垃圾回收介绍及GC算法详解
目录 引言 GC的作用域 什么是垃圾回收? 常见的GC算法 1.引用计数法 2.复制算法 3.标记清除 4.标记整理 小总结 5.分代收集算法 ps:可达性分析算法? 可达性分析的作用 可达性分析与垃圾回收算法的关系 结论 引言 在编程世界中,…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
