Pytorch为什么 nn.CrossEntropyLoss = LogSoftmax + nn.NLLLoss?
为什么 nn.CrossEntropyLoss = LogSoftmax + nn.NLLLoss?
在使用 PyTorch 时,我们经常听说 nn.CrossEntropyLoss 是 LogSoftmax 和 nn.NLLLoss 的组合。这句话听起来简单,但背后到底是怎么回事?为什么这两个分开的功能加起来就等于一个完整的交叉熵损失?今天我们就从数学公式到代码实现,彻底搞清楚它们的联系。
1. 先认识三个主角
要理解这个等式,先得知道每个部分的定义和作用:
nn.CrossEntropyLoss:交叉熵损失,直接接受未归一化的 logits,计算模型预测与真实标签的差距,适用于多分类任务。LogSoftmax:将 logits 转为对数概率(log probabilities),输出范围是负值。nn.NLLLoss:负对数似然损失,接受对数概率,计算正确类别的负对数值。
表面上看,nn.CrossEntropyLoss 是一个独立的损失函数,而 LogSoftmax 和 nn.NLLLoss 是两步操作。为什么说它们本质上是一回事呢?答案藏在数学公式和计算逻辑里。
2. 数学上的拆解
让我们从交叉熵的定义开始,逐步推导。
(1) 交叉熵的数学形式
交叉熵(Cross-Entropy)衡量两个概率分布的差异。在多分类任务中:
- ( p p p ):真实分布,通常是 one-hot 编码(比如
[0, 1, 0]表示第 1 类)。 - ( q q q ):预测分布,是模型输出的概率(比如
[0.2, 0.5, 0.3])。
交叉熵公式为:
H ( p , q ) = − ∑ c = 1 C p c log ( q c ) H(p, q) = -\sum_{c=1}^{C} p_c \log(q_c) H(p,q)=−c=1∑Cpclog(qc)
对于 one-hot 编码,( p c p_c pc ) 在正确类别上为 1,其他为 0,所以简化为:
H ( p , q ) = − log ( q correct ) H(p, q) = -\log(q_{\text{correct}}) H(p,q)=−log(qcorrect)
其中 ( q correct q_{\text{correct}} qcorrect ) 是正确类别对应的预测概率。对 ( N N N ) 个样本取平均,损失为:
Loss = − 1 N ∑ i = 1 N log ( q i , y i ) \text{Loss} = -\frac{1}{N} \sum_{i=1}^{N} \log(q_{i, y_i}) Loss=−N1i=1∑Nlog(qi,yi)
这正是交叉熵损失的核心。
(2) 从 logits 到概率
神经网络输出的是原始分数(logits),比如 ( z = [ z 1 , z 2 , z 3 ] z = [z_1, z_2, z_3] z=[z1,z2,z3] )。要得到概率 ( q q q ),需要用 Softmax:
q j = e z j ∑ k = 1 C e z k q_j = \frac{e^{z_j}}{\sum_{k=1}^{C} e^{z_k}} qj=∑k=1Cezkezj
交叉熵损失变成:
Loss = − 1 N ∑ i = 1 N log ( e z i , y i ∑ k = 1 C e z i , k ) \text{Loss} = -\frac{1}{N} \sum_{i=1}^{N} \log\left(\frac{e^{z_{i, y_i}}}{\sum_{k=1}^{C} e^{z_{i,k}}}\right) Loss=−N1i=1∑Nlog(∑k=1Cezi,kezi,yi)
这就是 nn.CrossEntropyLoss 的数学形式。
(3) 分解为两步
现在我们把这个公式拆开:
-
第一步:LogSoftmax
计算对数概率:
log ( q j ) = log ( e z j ∑ k = 1 C e z k ) = z j − log ( ∑ k = 1 C e z k ) \log(q_j) = \log\left(\frac{e^{z_j}}{\sum_{k=1}^{C} e^{z_k}}\right) = z_j - \log\left(\sum_{k=1}^{C} e^{z_k}\right) log(qj)=log(∑k=1Cezkezj)=zj−log(k=1∑Cezk)
这正是LogSoftmax的定义。它把 logits ( z z z ) 转为对数概率 ( log ( q ) \log(q) log(q) )。 -
第二步:NLLLoss
有了对数概率 ( log ( q ) \log(q) log(q) ),取出正确类别的值,取负号并平均:
NLL = − 1 N ∑ i = 1 N log ( q i , y i ) \text{NLL} = -\frac{1}{N} \sum_{i=1}^{N} \log(q_{i, y_i}) NLL=−N1i=1∑Nlog(qi,yi)
这就是nn.NLLLoss的公式。
组合起来:
LogSoftmax把 logits 转为 ( log ( q ) \log(q) log(q) )。nn.NLLLoss对 ( log ( q ) \log(q) log(q) ) 取负号,计算损失。- 两步合起来正好是 ( − log ( q correct ) -\log(q_{\text{correct}}) −log(qcorrect) ),与交叉熵一致。
3. PyTorch 中的实现验证
从数学上看,nn.CrossEntropyLoss 的确可以分解为 LogSoftmax 和 nn.NLLLoss。我们用代码验证一下:
import torch
import torch.nn as nn# 输入数据
logits = torch.tensor([[1.0, 2.0, 0.5], [0.1, 0.5, 2.0]]) # [batch_size, num_classes]
target = torch.tensor([1, 2]) # 真实类别索引# 方法 1:直接用 nn.CrossEntropyLoss
ce_loss_fn = nn.CrossEntropyLoss()
ce_loss = ce_loss_fn(logits, target)
print("CrossEntropyLoss:", ce_loss.item())# 方法 2:LogSoftmax + nn.NLLLoss
log_softmax = nn.LogSoftmax(dim=1)
nll_loss_fn = nn.NLLLoss()
log_probs = log_softmax(logits) # 计算对数概率
nll_loss = nll_loss_fn(log_probs, target)
print("LogSoftmax + NLLLoss:", nll_loss.item())
运行结果:两个输出的值完全相同(比如 0.75)。这证明 nn.CrossEntropyLoss 在内部就是先做 LogSoftmax,再做 nn.NLLLoss。
4. 为什么 PyTorch 这么设计?
既然 nn.CrossEntropyLoss 等价于 LogSoftmax + nn.NLLLoss,为什么 PyTorch 提供了两种方式?
-
便利性:
nn.CrossEntropyLoss是一个“一体式”工具,直接输入 logits 就能用,适合大多数场景,省去手动搭配的麻烦。 -
模块化:
LogSoftmax和nn.NLLLoss分开设计,给开发者更多灵活性:- 你可以在模型里加
LogSoftmax,只用nn.NLLLoss计算损失。 - 可以单独调试对数概率(比如打印
log_probs)。 - 在某些自定义损失中,可能需要用到独立的
LogSoftmax。
- 你可以在模型里加
-
数值稳定性:
nn.CrossEntropyLoss内部优化了计算,避免了分开操作时可能出现的溢出问题(比如 logits 很大时,Softmax 的分母溢出)。
5. 为什么不直接用 Softmax?
你可能好奇:为什么不用 Softmax + 对数 + 取负,而是用 LogSoftmax?
答案是数值稳定性:
- 单独计算
Softmax(指数运算)可能导致溢出(比如 ( e 1000 e^{1000} e1000 ))。 LogSoftmax把指数和对数合并为 ( z j − log ( ∑ e z k ) z_j - \log(\sum e^{z_k}) zj−log(∑ezk) ),计算更稳定。
6. 使用场景对比
-
nn.CrossEntropyLoss:- 输入:logits。
- 场景:标准多分类任务(图像分类、文本分类)。
- 优点:简单直接。
-
LogSoftmax+nn.NLLLoss:- 输入:logits 需手动转为对数概率。
- 场景:需要显式控制 Softmax,或者模型已输出对数概率。
- 优点:灵活性高。
7. 小结:为什么等价?
- 数学上:交叉熵 ( − log ( q correct ) -\log(q_{\text{correct}}) −log(qcorrect) ) 可以拆成两步:
LogSoftmax:从 logits 到 ( log ( q ) \log(q) log(q) )。nn.NLLLoss:从 ( log ( q ) \log(q) log(q) ) 到 ( − log ( q correct ) -\log(q_{\text{correct}}) −log(qcorrect) )。
- 实现上:
nn.CrossEntropyLoss把这两步封装成一个函数,结果一致。 - 设计上:PyTorch 提供两种方式,满足不同需求。
所以,nn.CrossEntropyLoss = LogSoftmax + nn.NLLLoss 不是巧合,而是交叉熵计算的自然分解。理解这一点,能帮助你更灵活地使用 PyTorch 的损失函数。
8. 彩蛋:手动推导
想自己验证?试试手动计算:
- logits
[1.0, 2.0, 0.5],目标是 1。 - Softmax:
[0.23, 0.63, 0.14]。 - LogSoftmax:
[-1.47, -0.47, -1.97]。 - NLL:
-(-0.47) = 0.47。 - 直接用
nn.CrossEntropyLoss,结果一样!
希望这篇博客解开了你的疑惑!
后记
2025年2月28日18点51分于上海,在grok3 大模型辅助下完成。
相关文章:

Pytorch为什么 nn.CrossEntropyLoss = LogSoftmax + nn.NLLLoss?
为什么 nn.CrossEntropyLoss LogSoftmax nn.NLLLoss? 在使用 PyTorch 时,我们经常听说 nn.CrossEntropyLoss 是 LogSoftmax 和 nn.NLLLoss 的组合。这句话听起来简单,但背后到底是怎么回事?为什么这两个分开的功能加起来就等于…...

Go入门之文件
以只读方式打开文件 package mainimport ("fmt""io""os" )func main() {file, err : os.Open("./main.go")defer file.Close()if err ! nil {fmt.Println(err)return}fmt.Println(file)var tempSlice make([]byte, 128)var strSlice…...

基因型—环境两向表数据分析——品种生态区划分
参考资料:农作物品种试验数据管理与分析 用于品种生态区划分的GGE双标图有两种功能图:试点向量功能图和“谁赢在哪里”功能图。双标图的具体模型基于SD定标和h加权和试点中心化的数据。本例中籽粒产量的GGE双标图仅解释了G和GE总变异的53.6%,…...

Leetcode2414:最长的字母序连续子字符串的长度
题目描述: 字母序连续字符串 是由字母表中连续字母组成的字符串。换句话说,字符串 "abcdefghijklmnopqrstuvwxyz" 的任意子字符串都是 字母序连续字符串 。 例如,"abc" 是一个字母序连续字符串,而 "ac…...

React(12)案例前期准备
1、创建项目 npx creat-react-app xxx 这里注意 react版本过高会导致antd组件无法安装 需要手动修改pagejson文件中的react和react-demo版本号为 18.2.0 npm i 在配置别名路径 创建craco文件 const path require("path"); module.exports {webpack: {alias: …...
)
2025年2月28日(RAG)
从图片中的内容来看,用户提到的“RAG”实际上是“Retrieval-Augmented Generation”的缩写,中文称为“检索增强生成”。这是一种结合了检索(Retrieval)和生成(Generation)的技术,用于增强自然语…...

python-leetcode-寻找重复数
287. 寻找重复数 - 力扣(LeetCode) class Solution:def findDuplicate(self, nums: List[int]) -> int:# Step 1: 找到环的相遇点slow nums[0]fast nums[0]# 使用快慢指针,直到相遇while True:slow nums[slow] # 慢指针走一步fast nu…...

Vue 3 中,如果 public 目录下的 .js 文件中有一个函数执行后生成数据,并希望将这些数据传递到组件中
在 Vue 3 中,如果 public 目录下的 .js 文件中有一个函数执行后生成数据,并希望将这些数据传递到组件中,可以使用 window.postMessage,但需要结合具体场景。以下是不同方法的详细说明: 方法 1:使用 window…...

ai大模型自动化测试-TensorFlow Testing 测试模型实例
AI大模型自动化测试是确保模型质量、可靠性和性能的关键环节,以下将从测试流程、测试内容、测试工具及测试挑战与应对几个方面进行详细介绍: 测试流程 测试计划制定 确定测试目标:明确要测试的AI大模型的具体功能、性能、安全性等方面的目标,例如评估模型在特定任务上的准…...

初阶MySQL(两万字全面解析)
文章目录 1.初识MySQL1.1数据库1.2查看数据库1.3创建数据库1.4字符集编码和排序规则1.5修改数据库1.6删除数据库 2.MySQL常用数据类型和表的操作2.(一)常用数据类型1.数值类2.字符串类型3.二进制类型4.日期类型 2.(二)表的操作1查看指定库中所有表2.创建表 3.查看表结构和查看表…...

数据库数据恢复—SQL Server附加数据库报错“错误 823”怎么办?
SQL Server数据库附加数据库过程中比较常见的报错是“错误 823”,附加数据库失败。 如果数据库有备份则只需还原备份即可。但是如果没有备份,备份时间太久,或者其他原因导致备份不可用,那么就需要通过专业手段对数据库进行数据恢复…...

SpringBatch简单处理多表批量动态更新
项目需要处理一堆表,这些表数据量不是很大都有经纬度信息,但是这些表的数据没有流域信息,需要按经纬度信息计算所属流域信息。比较简单的项目,按DeepSeek提示思索完成开发,AI真好用。 阿里AI个人版本IDEA安装 IDEA中使…...

夜莺监控 - 边缘告警引擎架构详解
前言 夜莺类似 Grafana 可以接入多个数据源,查询数据源的数据做告警和展示。但是有些数据源所在的机房和中心机房之间网络链路不好,如果由 n9e 进程去周期性查询数据并判定告警,那在网络链路抖动或拥塞的时候,告警就不稳定了。所…...

18440二维差分
18440二维差分 ⭐️难度:中等 📖 📚 import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner new Scanner(System.in);int n scanner.nextInt();int m scanner.nextInt();int q scanne…...

安全传输,高效共享 —— 体验FileLink的跨网文件传输
在当今数字化转型的浪潮中,企业在进行跨网文件传输时面临诸多挑战,包括数据安全、传输速度和用户体验等。为了解决这些问题,FileLink应运而生,成为一款高效、安全的跨网文件传输解决方案。 一、FileLink的核心特点 1.加密技术 …...

SOME/IP 教程知识点总结
总结关于SOME/IP的教程,首先通读整个文件,理解各个部分的内容。看起来这个教程从介绍开始,讲到了为什么在车辆中使用以太网,然后详细讲解了SOME/IP的概念、序列化、消息传递、服务发现(SOME/IP-SD)、发布/订阅机制以及支持情况。 首先,我需要确认每个章节的主要知识点。…...

学习路程八 langchin核心组件 Models补充 I/O和 Redis Cache
前序 之前了解了Models,Prompt,但有些资料又把这块与输出合称为模型输入输出(Model I/O):这是与各种大语言模型进行交互的基本组件。它允许开发者管理提示(prompt),通过通用接口调…...

图书数据采集:使用Python爬虫获取书籍详细信息
文章目录 一、准备工作1.1 环境搭建1.2 确定目标网站1.3 分析目标网站二、采集豆瓣读书网站三、处理动态加载的内容四、批量抓取多本书籍信息五、反爬虫策略与应对方法六、数据存储与管理七、总结在数字化时代,图书信息的管理和获取变得尤为重要。通过编写Python爬虫,可以从各…...

【DeepSeek系列】05 DeepSeek核心算法改进点总结
文章目录 一、DeepSeek概要二、4个重要改进点2.1 多头潜在注意力2.2 混合专家模型MoE2.3 多Token预测3.4 GRPO强化学习策略 三、2个重要思考3.1 大规模强化学习3.2 蒸馏方法:小模型也可以很强大 一、DeepSeek概要 2024年~2025年初,DeepSeek …...
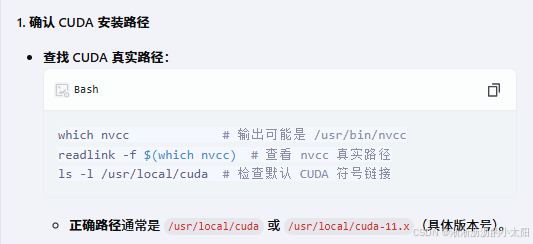
安装pointnet2-ops库
由于服务器没有连网,现在已在github中下载pointnet2_ops文件包并上传到服务器 (首先保证cuda版本和pytorch版本对应) 如何查找cuda的安装路径: 然后执行安装命令即可。...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...
