算法训练(leetcode)二刷第三十八天 | 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和、392. 判断子序列
刷题记录
- 1143. 最长公共子序列
- 1035. 不相交的线
- 53. 最大子数组和
- 动态规划
- 优化版
- 392. 判断子序列
1143. 最长公共子序列
leetcode题目地址
本题和300. 最长递增子序列相似(题解)。
使用动态规划:
- dp数组含义:dp[i][j]表示 以text1[i-1]结尾的子串A 和 以text2[j-1]结尾的子串B 的最长公共子序列的长度。
- 思路同300. 最长递增子序列,每个状态更新基于前面的状态,为了防止越界,dp数组下标从1开始。
- 状态转移方程:
- 当 text1[i-1] == text2[j-1] 时,dp[i][j] = dp[i-1][j-1] + 1;
- 当 text1[i-1] == text2[j-1] 时,dp[i][j] = max(dp[i-1][j], dp[i][j-1])
- 这里解释一下 max(dp[i-1][j], dp[i][j-1]) 的含义:由于dp数组存储的是两个子串的最长公共子序列的长度,当两个子串的单个字符不匹配时,对应下标处的dp值要赋值为前面子串的匹配情况取最长,即dp[i-1][j]表示以text1[i-2]结尾的子串A和以text2[j-1]结尾的子串B 的最长公共子序列的长度,dp[i][j-1]表示以text1[i-1]结尾的子串A和以text2[j-2]结尾的子串B 的最长公共子序列的长度。
时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
// java
class Solution {public int longestCommonSubsequence(String text1, String text2) {int len1 = text1.length(), len2 = text2.length();char[] arr1 = text1.toCharArray(), arr2 = text2.toCharArray();int[][] dp = new int[len1+1][len2+1];for(int i = 1; i <= len1; i++){for (int j = 1; j <= len2; j++){if(arr1[i-1] == arr2[j-1]){dp[i][j] = dp[i-1][j-1] + 1;} else{dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]);}// System.out.print(dp[j] + " ");}// System.out.println();}return dp[len1][len2];}
}
1035. 不相交的线
leetcode题目地址
本题其实与上一题1143. 最长公共子序列的思路完全一致。题目的描述时要求找不相交的线的最大连线数,而不相交的线其实就是找两个序列的公共子序列(不相交就是两个子序列在原序列中相对顺序一致)。
时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
// java
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int len1 = nums1.length, len2 = nums2.length;int[][] dp = new int[len1+1][len2+1];for(int i=1; i<=len1; i++){for(int j=1; j<=len2; j++){if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1] + 1;} else{dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);}}}return dp[len1][len2];}
}
53. 最大子数组和
leetcode题目地址
-
dp数组含义:
dp[i]表示以nums[i]结尾(包含)的最大子数组和 -
状态转移方程:
dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);- dp[i-1] + nums[i]表示上一个(以nums[i-1]结尾的)子序列加入当前nums[i]
- nums[i]表示从当前元素开始从头计算(仅包含当前元素的子序列)
-
初始化:
dp[i]表示以nums[i]结尾(包含)的最大子数组和,因此dp[0]初始化为nums[0],后面状态均为0.
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
动态规划
// java
class Solution {public int maxSubArray(int[] nums) {int len = nums.length;int[] dp = new int[len];dp[0] = nums[0];int result = nums[0];for(int i=1; i<len; i++){dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);result = Math.max(dp[i], result);}return result;}
}
优化版
可以看到在动规中每个状态的更新都仅依赖于前一个状态,因此无需使用数组,仅使用一个变量来记录前一个状态。
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
// java
class Solution {public int maxSubArray(int[] nums) {int len = nums.length;int res = nums[0];int result = nums[0];for(int i=1; i<len; i++){res = Math.max(res + nums[i], nums[i]);result = Math.max(res, result);}return result;}
}392. 判断子序列
leetcode题目地址
本题本质上依旧是寻找最长公共子序列。给定s和t,判断s是否是t的子序列,也就是查看s和t的最长公共子序列长度是否等于s的长度。
- dp数组含义:
dp[i][j]表示 以s[i-1]结尾的子串A 和 以t[j-1]结尾的子串B 的最长公共子序列。 - 状态转移方程:
- 当s[i-1] == t[j-1]时,dp[i][j] = dp[i-1][j-1] + 1;
- 当s[i-1] != t[j-1]时,dp[i][j] = dp[i][j-1];
这里不匹配时为什么是 dp[i][j] = dp[i][j-1] 而不是 dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1])
因为是在t中查找s是否是子序列,因此在不匹配时,只能删除t中的字符来查看分别以s[i-1]和t[j-2]结尾的子串的匹配情况。
而1143. 最长公共子序列不给定谁为子串,因此需要分别考虑各自为另一个字符串的子串的情况。
时间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
空间复杂度: O ( n ∗ m ) O(n*m) O(n∗m)
// java
class Solution {public boolean isSubsequence(String s, String t) {char[] sArry = s.toCharArray();char[] tArry = t.toCharArray();int len1 = s.length(), len2 = t.length();int[][] dp = new int[len1+1][len2+1];for(int i=1; i<=len1; i++){for(int j=1; j<=len2; j++){if(sArry[i-1] == tArry[j-1]){dp[i][j] = dp[i-1][j-1] + 1;} else {dp[i][j] = dp[i][j-1];}// System.out.print(dp[i][j] + " ");}// System.out.println();}return dp[len1][len2] == len1;}
}
相关文章:
二刷第三十八天 | 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和、392. 判断子序列)
算法训练(leetcode)二刷第三十八天 | 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和、392. 判断子序列
刷题记录 1143. 最长公共子序列1035. 不相交的线53. 最大子数组和动态规划优化版 392. 判断子序列 1143. 最长公共子序列 leetcode题目地址 本题和300. 最长递增子序列相似(题解)。 使用动态规划: dp数组含义:dp[i][j]表示 以…...

【JavaWeb学习Day20】
Tlias智能学习系统 员工登录 三层架构: Controller:1.接收请求参数(用户名,密码)2.调用Service方法3.响应结果 具体实现: /*** 登录*/ PostMapping("/login") public Result login(Reque…...
等级考试试卷(二级)真题 + 答案)
2024年12月中国电子学会青少年软件编程(Python)等级考试试卷(二级)真题 + 答案
青少年软件编程(Python)等级考试试卷(二级) ↓↓↓↓↓↓ 模拟 分数:100 题数:37 一、单选题(共25题,共50分) 1. 已知字典如下 dic1 = { name: Ming, age:20, grade: A, Tel:6666666 } 以下哪个代码运行结果为20?( ) A. dic1(age) B. dic1[1] C. dic1(20) D. dic1[ag…...

一、对iic类模块分析与使用
bmp280驱动代码 说明: 1、该模块用于获取气压,温度,海拔等数据。 vcc,gnd接电源 sda ,scl 接iic通信引脚 2、该模块使用iic通信,通过iic发送请求相关类的寄存器值,芯片获取对应寄存器返回的数据…...
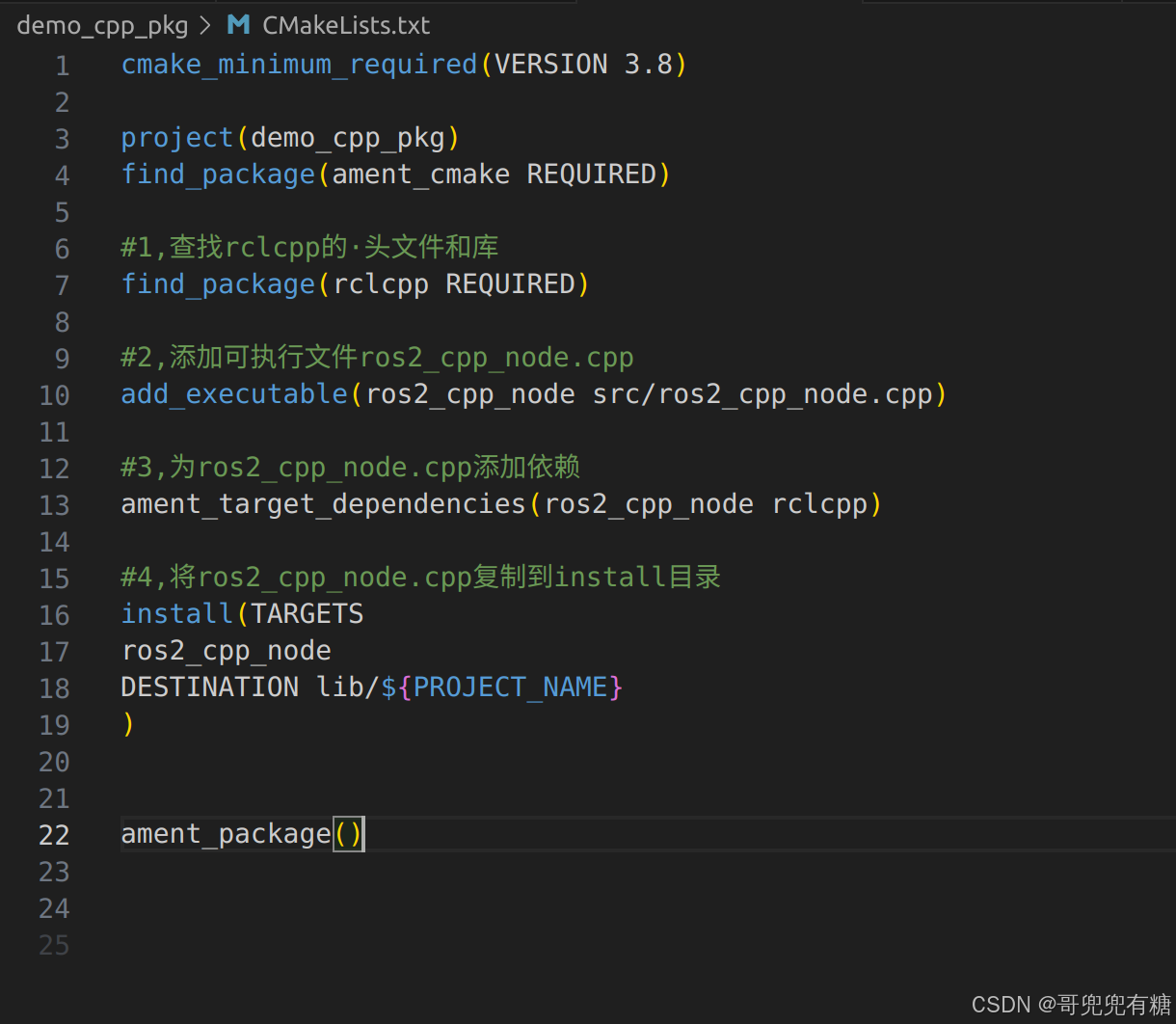
ROS 2机器人开发--CMakeLists.txt 文件详解
很多小白宝宝不懂CMakeLists.txt 究竟是干什么的,本文对CMakeLists.txt 文件进行详解 CMakeLists.txt 是 CMake 的核心文件,用户通过这个文件告诉 CMake 如何构建项目。这个文件通常包括设置项目名称、版本号、语言标准、编译器选项、查找依赖包、添加可…...

kan与小波,和不知所云的画图
文章目录 小波应用范围与pde小波的名字 画图图(a):数值解向量 \( u \)图(b):数值解向量 \( v \)结论图4 小波 在你提供的代码中,小波变换(Wavelet Transform)被用于 KANLinear 类中。具体来说,小波变换在 …...

使用DeepSeek实现自动化编程:类的自动生成
目录 简述 1. 通过注释生成C类 1.1 模糊生成 1.2 把控细节,让结果更精准 1.3 让DeepSeek自动生成代码 2. 验证DeepSeek自动生成的代码 2.1 安装SQLite命令行工具 2.2 验证DeepSeek代码 3. 测试代码下载 简述 在现代软件开发中,自动化编程工具如…...

算法题:快速排序
一、快速排序 1、快速排序总结 快速排序是一种高效的排序算法,基于分治法的思想。 分区操作是快速排序的核心,将数组分为两部分。 原地分区可以减少空间复杂度,提高效率。 快速排序的平均时间复杂度为 O(n log n),但在最坏情况…...

Python的那些事第三十六篇:基于 Vega 和 Vega-Lite 的数据可视化解决方案,Altair 声明式可视化库
Altair 声明式可视化库:基于 Vega 和 Vega-Lite 的数据可视化解决方案 摘要 在数据科学和分析领域,有效的数据可视化是理解数据、发现模式和传达见解的关键。Python 作为数据科学的主要编程语言之一,提供了多种数据可视化库。其中,Altair 是一个基于 Vega 和 Vega-Lite 的…...

aws(学习笔记第三十课) 练习使用transit gateway
aws(学习笔记第三十课) 使用transit gateway 学习内容: 什么是transit gateway构造两个vpc,并且使用session manager访问private subnet的ec2练习使用transit gateway 1. 什么是transit gateway Transit Gateway的概念 Transit Gateway就是VPC和OnPro…...

Phpstudy中的MySQL无法正常启动或启动后自动暂停,以及sqlilab环境搭建出现的问题解决方法
【解决方法】 无法启动的原因是Phpstudy中的MySQL与本地的mysql重名,导致无法正常启动;所以这时我们就需要将本地的MySQL进行修改名称; 或者修改phpstudy中数据库的端口号,但是我觉得还是不是很好解决这种问题 最后一个方法&#…...

【Android】安卓付款密码输入框、支付密码输入框
如图 代码部分: public class PayPasswordDialog extends AppCompatDialogFragment {private String mPayPass "";private String mTitle, mMoney;private final TextView[] mPayPassTextViewArray new TextView[6];private List<Integer> mPayP…...

Python异常处理:从入门到精通的实用指南
Langchain系列文章目录 01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南 02-玩转 LangChain Memory 模块:四种记忆类型详解及应用场景全覆盖 03-全面掌握 LangChain:从核心链条构建到动态任务分配的实战指南 04-玩转 LangChai…...

【AVL树】—— 我与C++的不解之缘(二十三)
什么是AVL树? AVL树发明者是G. M. Adelson-Velsky和E. M. Landis两个前苏联科学家,他们在1962年论文《An algorithm for the organization of information》中发表了AVL树。AVL树是最先发明的自平衡二叉搜索树,说白了就是能够自己控制平衡结构…...

用大白话解释日志处理Log4j 是什么 有什么用 怎么用
Log4j是什么? Log4j就像程序的“黑匣子”,专门用来记录软件运行时的各种信息,比如哪里报错、性能如何、用户操作轨迹等。它是Java领域最常用的日志框架之一,可以灵活控制日志内容、输出位置(控制台、文件、数据库等&a…...

无人机遥控器的亮度 和 两个工作频率
工作频率 2.4000-2.4835 GHz , 5.725-5.850 GHz 1.这是一个无人机的遥控器的两个工作频率,为什么会有两个工作频率? 无人机的遥控器采用双频段设计(2.4GHz 和 5.8GHz),主要是为了解决以下问题并优化性…...

【Linux】命令行参数 | 环境变量(四)
目录 前言: 一、命令行参数: 1.main函数参数 2.为什么有它? 二、环境变量: 1.main函数第三个参数 2.查看shell本身环境变量 3.PATH环境变量 4.修改PATH环境变量配置文件 5.HOME环境变量 6.SHELL环境变量 7.PWD环境变…...

算法002——复写零
力扣——复写零点击即可跳转 这道题还是运用 双指针,我们从左往右开始,让 cur 0,dest 0,当我们循环时,会覆盖后面的值,所以从左到右无法实现,我们运用 从右到左的方式。 以示例一数组为例,从…...

例子 DQN + CartPole: 深入思考一下,强化学习确实是一场智能冒险之旅!
强化学习的概念 在技术人员眼里,深度学习、强化学习,或者是大模型,都只是一些算法。无论是简单,还是复杂,我们都是平静的看待。当商业元素日益渗透进技术领域,人人言必称大模型的时候。技术人该反思一下&a…...

java 实现xxl-job定时任务自动注册到调度中心
xxl-job 自动注册(执行器和任务) 前言 xxl-job是一个功能强大、简单易用、高可用且可扩展性强的分布式定时任务框架/分布式任务调度平台。它适用于各种需要定时任务调度的场景,并可根据业务需求进行灵活配置和扩展。 xxl-job简介 xxl-job是一个开源的分布式定时任务框架,…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
