认知动力学视角下的生命优化系统:多模态机器学习框架的哲学重构
认知动力学视角下的生命优化系统:多模态机器学习框架的哲学重构
一、信息熵与生命系统的耗散结构
在热力学第二定律框架下,生命系统可视为负熵流的耗散结构:
d S = d i S + d e S dS = d_iS + d_eS dS=diS+deS
其中 d i S d_iS diS为内部熵增, d e S d_eS deS为外部熵减。根据香农信息论5,"他强任他强"的智慧对应信息熵的稳定控制策略:
H ( X ) = − ∑ i = 1 n p ( x i ) log p ( x i ) ≤ C H(X) = -\sum_{i=1}^n p(x_i)\log p(x_i) \leq C H(X)=−i=1∑np(xi)logp(xi)≤C
通过构建自适应信息滤波器,系统实现外界扰动 ∇ H e x t \nabla H_{ext} ∇Hext与内部耗散 ∇ H i n t \nabla H_{int} ∇Hint的动态平衡。研究表明,当批评声量 I c r i t i q u e I_{critique} Icritique满足:
∂ H ∂ t = ∇ ⋅ ( D ∇ H ) + k I c r i t i q u e 2 \frac{\partial H}{\partial t} = \nabla \cdot (D\nabla H) + kI_{critique}^2 ∂t∂H=∇⋅(D∇H)+kIcritique2
其中扩散系数 D D D表征心理韧性,k为认知转换率,此时系统进入自组织临界状态5。
二、符号操作系统的认知架构
人类思维本质符合物理符号系统假设2:
Σ = { S , O , T , τ } \Sigma = \{S, O, T, \tau\} Σ={S,O,T,τ}
- S S S:符号集合(如"压力"、"成长"等概念)
- O O O:操作规则(认知重构机制)
- T T T:时间演化算子
- τ \tau τ:转移函数
当遭遇压力事件 E p E_p Ep时,符号系统执行认知重编码:
E p ′ = τ ( E p ⊗ M e x p ) E'_p = \tau(E_p \otimes M_{exp}) Ep′=τ(Ep⊗Mexp)
其中 M e x p M_{exp} Mexp为经验矩阵。这种符号操作机制2解释了为何相同压力源在不同个体产生差异化响应,其认知重构效率 η c o g \eta_{cog} ηcog可量化为:
η c o g = ∥ W p o s ∥ 1 ∥ W p o s ∥ 1 + ∥ W n e g ∥ 1 \eta_{cog} = \frac{\|W_{pos}\|_1}{\|W_{pos}\|_1 + \|W_{neg}\|_1} ηcog=∥Wpos∥1+∥Wneg∥1∥Wpos∥1
式中 W p o s W_{pos} Wpos、 W n e g W_{neg} Wneg分别为正向/负向语义权重向量。
三、因果推断与压力响应机制
压力应对本质是因果图模型的结构学习问题3:
G = ⟨ V , E ⟩ G = \langle V, E \rangle G=⟨V,E⟩
顶点集 V = { X , Y , Z } V = \{X, Y, Z\} V={X,Y,Z}分别代表压力源、应对策略、结果变量。通过do-calculus进行反事实推理:
P ( Y ∣ d o ( X = x ) ) = ∑ z P ( Y ∣ X = x , Z = z ) P ( Z = z ) P(Y|do(X=x)) = \sum_z P(Y|X=x,Z=z)P(Z=z) P(Y∣do(X=x))=z∑P(Y∣X=x,Z=z)P(Z=z)
这为"压榨转成长"提供了形式化解释。当引入混淆变量 U U U时,需使用双重稳健估计量3:
τ ^ D R = 1 n ∑ i = 1 n [ T i ( Y i − Q ^ 1 ( X i ) ) e ^ ( X i ) + Q ^ 1 ( X i ) − ( 1 − T i ) ( Y i − Q ^ 0 ( X i ) ) 1 − e ^ ( X i ) − Q ^ 0 ( X i ) ] \hat{τ}_{DR} = \frac{1}{n}\sum_{i=1}^n[\frac{T_i(Y_i - \hat{Q}_1(X_i))}{\hat{e}(X_i)} + \hat{Q}_1(X_i) - \frac{(1-T_i)(Y_i - \hat{Q}_0(X_i))}{1-\hat{e}(X_i)} - \hat{Q}_0(X_i)] τ^DR=n1i=1∑n[e^(Xi)Ti(Yi−Q^1(Xi))+Q^1(Xi)−1−e^(Xi)(1−Ti)(Yi−Q^0(Xi))−Q^0(Xi)]
四、注意力机制的认知资源分配
借鉴Transformer模型4,压力应对可建模为多头注意力分布:
MultiHead ( Q , K , V ) = Concat ( h e a d 1 , . . . , h e a d h ) W O \text{MultiHead}(Q,K,V) = \text{Concat}(head_1,...,head_h)W^O MultiHead(Q,K,V)=Concat(head1,...,headh)WO
其中每个注意力头对应不同认知维度:
h e a d i = softmax ( Q W i Q ( K W i K ) T d k ) V W i V head_i = \text{softmax}(\frac{QW_i^Q(KW_i^K)^T}{\sqrt{d_k}})VW_i^V headi=softmax(dkQWiQ(KWiK)T)VWiV
通过调节注意力权重矩阵 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV,系统实现:
- 核心压力聚焦(主注意力头)
- 边缘焦虑抑制(残差连接)
- 长期记忆整合(位置编码)
五、正则化框架下的失败解读
经验风险最小化需引入弹性网络正则化4:
min θ 1 2 n ∥ y − X θ ∥ 2 + λ ( ρ ∥ θ ∥ 1 + 1 − ρ 2 ∥ θ ∥ 2 2 ) \min_θ \frac{1}{2n}\|y - Xθ\|^2 + λ(ρ\|θ\|_1 + \frac{1-ρ}{2}\|θ\|_2^2) θmin2n1∥y−Xθ∥2+λ(ρ∥θ∥1+21−ρ∥θ∥22)
其动力学解释为:
- L1范数:关键经验强化(认知锚点)
- L2范数:无效执念消解(认知扩散)
- 混合系数ρ:心理弹性参数
当失败经验 D f a i l D_{fail} Dfail输入系统时,参数更新遵循:
θ t + 1 = θ t − η t ( ∇ L ( θ t ) + λ sign ( θ t ) ) θ_{t+1} = θ_t - η_t(\nabla L(θ_t) + λ\text{sign}(θ_t)) θt+1=θt−ηt(∇L(θt)+λsign(θt))
六、贝叶斯推理与认知进化
认知更新符合贝叶斯概率图模型5:
P ( H ∣ D ) = P ( D ∣ H ) P ( H ) P ( D ) P(H|D) = \frac{P(D|H)P(H)}{P(D)} P(H∣D)=P(D)P(D∣H)P(H)
引入鲁棒贝叶斯推断3:
P r o b u s t ( θ ∣ D ) = arg min Q ∈ P D K L ( Q ∣ ∣ P ) + E Q [ L ( θ , D ) ] P_{robust}(θ|D) = \arg\min_{Q∈\mathcal{P}} D_{KL}(Q||P) + \mathbb{E}_Q[L(θ,D)] Probust(θ∣D)=argQ∈PminDKL(Q∣∣P)+EQ[L(θ,D)]
该框架具有:
- 先验修正机制( P ( H ) P(H) P(H)动态调整)
- 证据加权策略( P ( D ∣ H ) P(D|H) P(D∣H)自适应缩放)
- 抗扰动能力(KL散度约束)
七、超参数优化与心理调适
心智系统的超参数空间可建模为:
H = { η , β , γ , λ } ∈ R d \mathcal{H} = \{η, β, γ, λ\} \in \mathbb{R}^d H={η,β,γ,λ}∈Rd
通过贝叶斯优化3寻找帕累托最优解:
x t + 1 = arg max x μ t ( x ) + κ t σ t ( x ) x_{t+1} = \arg\max_x μ_t(x) + κ_tσ_t(x) xt+1=argxmaxμt(x)+κtσt(x)
其中:
- 均值函数μ:经验收益预测
- 方差函数σ:探索潜力评估
- 平衡系数κ:风险偏好参数
八、分布式表征与自我实现
终极优化目标函数整合为4:
min θ E ( x , y ) ∼ D [ L ( f θ ( x ) , y ) ] + λ 1 Ω ( θ ) + λ 2 E x [ H ( p θ ( y ∣ x ) ) ] + λ 3 I ( x ; y ) \min_θ \mathbb{E}_{(x,y)\sim\mathcal{D}}[L(f_θ(x),y)] + λ_1Ω(θ) + λ_2\mathbb{E}_x[H(p_θ(y|x))] + λ_3I(x;y) θminE(x,y)∼D[L(fθ(x),y)]+λ1Ω(θ)+λ2Ex[H(pθ(y∣x))]+λ3I(x;y)
其中:
- 信息熵项 H H H:维持认知开放性
- 互信息项 I I I:增强现实关联性
- 正则项Ω:防止过拟合困境
九、元学习框架下的生存策略
构建MAML(Model-Agnostic Meta-Learning)范式4:
min θ ∑ T i ∼ p ( T ) L T i ( θ − α ∇ θ L T i ( θ ) ) \min_θ \sum_{\mathcal{T}_i \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i}(θ - α\nabla_θ\mathcal{L}_{\mathcal{T}_i}(θ)) θminTi∼p(T)∑LTi(θ−α∇θLTi(θ))
该算法实现:
- 快速适应新压力环境(内循环更新)
- 提取跨领域元知识(外循环优化)
- 平衡泛化与特化(梯度对齐机制)
十、量子认知与意识叠加态
引入量子概率模型5解释矛盾心态:
∣ ψ ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ |\psi\rangle = α|0\rangle + β|1\rangle ∣ψ⟩=α∣0⟩+β∣1⟩
其中:
- ∣ 0 ⟩ |0\rangle ∣0⟩:积极认知基态
- ∣ 1 ⟩ |1\rangle ∣1⟩:消极认知基态
- 概率幅 ∣ α ∣ 2 + ∣ β ∣ 2 = 1 |α|^2 + |β|^2 = 1 ∣α∣2+∣β∣2=1
决策过程遵循量子干涉原理:
P ( x ) = ∣ ∑ i ψ i ( x ) ∣ 2 P(x) = |\sum_i ψ_i(x)|^2 P(x)=∣i∑ψi(x)∣2
注:高维认知流形中的量子隧穿效应,解释顿悟现象的发生机制5
十一、神经符号系统的认知跃迁
融合联结主义与符号主义2:
A N S = σ ( W ⋅ ϕ ( S ) + b ) A_{NS} = σ(W \cdot ϕ(S) + b) ANS=σ(W⋅ϕ(S)+b)
其中:
- ϕ ( S ) ϕ(S) ϕ(S):符号嵌入层
- W W W:神经权重矩阵
- σ σ σ:非线性激活函数
该系统实现:
- 符号逻辑推理(显式知识处理)
- 亚符号计算(隐式模式识别)
- 认知蒸馏(知识迁移机制)
十二、因果强化学习框架
构建DRL(Dual Reinforcement Learning)模型3:
Q π ( s , a ) = E π [ ∑ k = 0 ∞ γ k r t + k ∣ s t = s , a t = a ] Q^{π}(s,a) = \mathbb{E}_π[\sum_{k=0}^∞ γ^k r_{t+k} | s_t=s, a_t=a] Qπ(s,a)=Eπ[k=0∑∞γkrt+k∣st=s,at=a]
引入反事实回报估计:
Q ^ C F ( s , a ) = Q ( s , a ) + E [ R ∣ d o ( A = a ) ] − E [ R ∣ d o ( A = π ( s ) ) ] \hat{Q}_{CF}(s,a) = Q(s,a) + \mathbb{E}[R|do(A=a)] - \mathbb{E}[R|do(A=π(s))] Q^CF(s,a)=Q(s,a)+E[R∣do(A=a)]−E[R∣do(A=π(s))]
十三、拓扑数据分析与认知演化
采用持续同调方法4分析认知拓扑:
H k ( X ε ) = Z k ( X ε ) / B k ( X ε ) H_k(X_ε) = Z_k(X_ε)/B_k(X_ε) Hk(Xε)=Zk(Xε)/Bk(Xε)
其中:
- X ε X_ε Xε:认知状态复形
- Z k Z_k Zk:循环群
- B k B_k Bk:边缘群
持久图(persistence diagram)揭示:
- 核心认知结构(长生存周期特征)
- 临时心理状态(短生存周期噪声)
- 认知相变点(拓扑结构突变)
十四、微分几何视角下的成长轨迹
在黎曼流形 M \mathcal{M} M上定义认知发展路径:
D d t = ∇ γ ˙ ( t ) γ ˙ ( t ) = 0 \frac{D}{dt} = \nabla_{\dot{γ}(t)}\dot{γ}(t) = 0 dtD=∇γ˙(t)γ˙(t)=0
其测地线方程解:
γ ¨ k + Γ i j k γ ˙ i γ ˙ j = 0 \ddot{γ}^k + Γ_{ij}^k \dot{γ}^i \dot{γ}^j = 0 γ¨k+Γijkγ˙iγ˙j=0
克里斯托弗符号 Γ i j k Γ_{ij}^k Γijk编码了:
- 经验曲率张量
- 学习速率联络
- 认知挠率场
十五、随机微分方程与命运概率
构建认知演化SDE模型:
d X t = μ ( X t , t ) d t + σ ( X t , t ) d W t dX_t = μ(X_t,t)dt + σ(X_t,t)dW_t dXt=μ(Xt,t)dt+σ(Xt,t)dWt
其福克-普朗克方程描述概率密度演化:
∂ p ∂ t = − ∇ ⋅ ( μ p ) + 1 2 ∇ 2 ( σ 2 p ) \frac{\partial p}{\partial t} = -\nabla\cdot(μp) + \frac{1}{2}\nabla^2(σ^2p) ∂t∂p=−∇⋅(μp)+21∇2(σ2p)
通过调节漂移项μ和扩散项σ,系统可实现:
- 目标导向性(漂移场设计)
- 探索随机性(噪声注入)
- 稳定收敛域(势阱构造)
“生命的最优控制问题,本质上是在非合作博弈中寻找纳什均衡。” —— 基于认知博弈论的现代诠释3,5
本框架通过15个维度构建认知计算的统一场论,将压力响应、失败解读、成长机制等生存命题,转化为可计算、可优化、可验证的数学对象。这种形式化重构不仅为传统智慧提供数理基础,更为构建人工通用智能(AGI)的认知架构开辟了新路径。在超曲面的人生流形上,每个临界点都是认知相变的契机,每次梯度更新都是心智的跃迁。
相关文章:

认知动力学视角下的生命优化系统:多模态机器学习框架的哲学重构
认知动力学视角下的生命优化系统:多模态机器学习框架的哲学重构 一、信息熵与生命系统的耗散结构 在热力学第二定律框架下,生命系统可视为负熵流的耗散结构: d S d i S d e S dS d_iS d_eS dSdiSdeS 其中 d i S d_iS diS为内部熵…...

Metal 学习笔记五:3D变换
在上一章中,您通过在 vertex 函数中计算position,来平移顶点和在屏幕上移动对象。但是,在 3D 空间中,您还想执行更多操作,例如旋转和缩放对象。您还需要一个场景内摄像机,以便您可以在场景中移动。 要移动…...

unity学习56:旧版legacy和新版TMP文本输入框 InputField学习
目录 1 旧版文本输入框 legacy InputField 1.1 新建一个文本输入框 1.2 InputField 的子物体构成 1.3 input field的的component 1.4 input Field的属性 2 过渡 transition 3 控件导航 navigation 4 占位文本 placeholder 5 文本 text 5.1 文本内容,用户…...

32位,算Cache地址
32位,算Cache地址...

C++蓝桥杯基础篇(六)
片头 嗨~小伙伴们,大家好!今天我们来一起学习蓝桥杯基础篇(六),练习相关的数组习题,准备好了吗?咱们开始咯! 第1题 数组的左方区域 这道题,实质上是找规律,…...

React 常见面试题及答案
记录面试过程 常见问题,如有错误,欢迎批评指正 1. 什么是虚拟DOM?为什么它提高了性能? 虚拟DOM是React创建的一个轻量级JavaScript对象,表示真实DOM的结构。当状态变化时,React会生成新的虚拟DOM…...

和鲸科技推出人工智能通识课程解决方案,助力AI人才培养
2025年2月,教育部副部长吴岩应港澳特区政府邀请,率团赴港澳宣讲《教育强国建设规划纲要 (2024—2035 年)》。在港澳期间,吴岩阐释了教育强国目标的任务,并与特区政府官员交流推进人工智能人才培养的办法。这一系列行动体现出人工智…...

免费使用 DeepSeek API 教程及资源汇总
免费使用 DeepSeek API 教程及资源汇总 一、DeepSeek API 资源汇总1.1 火山引擎1.2 百度千帆1.3 阿里百炼1.4 腾讯云 二、其他平台2.1 华为云2.2 硅基流动 三、总结 DeepSeek-R1 作为 2025 年初发布的推理大模型,凭借其卓越的逻辑推理能力和成本优势,迅速…...

网络安全-使用DeepSeek来获取sqlmap的攻击payload
文章目录 概述DeepSeek使用创建示例数据库创建API测试sqlmap部分日志参考 概述 今天来使用DeepSeek做安全测试,看看在有思路的情况下实现的快不快。 DeepSeek使用 我有一个思路,想要测试sqlmap工具如何dump数据库的: 连接mysql数据库&#…...

网络原理--TCP/IP(2)
我们在之前已经介绍到TCP协议的核心机制二,接下来我们将继续介绍其他的核心机制。 核心机制三:连接管理 即建立连接,断开连接,在正常情况下,TCP要经过三次握⼿建⽴连接,四次挥⼿断开连接。 建立连接:TCP是通过“三次握手” 在生活中的握手就是打招呼,,但握手操作没有…...

Ragflow与Dify之我见:AI应用开发领域的开源框架对比分析
本文详细介绍了两个在AI应用开发领域备受关注的开源框架:Ragflow和Dify。Ragflow专注于构建基于检索增强生成(RAG)的工作流,强调模块化和轻量化,适合处理复杂文档格式和需要高精度检索的场景。Dify则旨在降低大型语言模…...

文件上传漏洞绕过WAF
文件上传漏洞绕过WAF学习笔记 1. WAF检测原理 WAF(Web应用防火墙)通过以下方式拦截文件上传攻击: 关键字匹配:检测文件名、内容中的敏感词(如<?php、eval)。 扩展名黑名单:拦截.php、.jsp…...
[含文档+PPT+源码等]精品基于Python实现的vue3+Django计算机课程资源平台
基于Python实现的Vue3Django计算机课程资源平台的背景,可以从以下几个方面进行阐述: 一、教育行业发展背景 1. 教育资源数字化趋势 随着信息技术的快速发展,教育资源的数字化已成为不可逆转的趋势。计算机课程资源作为教育领域的重要组成部…...

Qt 开源音视频框架模块之QtAV播放器实践
Qt 开源音视频框架模块QtAV播放器实践 1 摘要 QtAV是一个基于Qt的多媒体框架,旨在简化音视频播放和处理。它是一个跨平台的库,支持多种音视频格式,并提供了一个简单易用的API来集成音视频功能。QtAV的设计目标是为Qt应用程序提供强大的音视…...

【前端】XML,XPATH,与HTML的关系
XML与HTML关系 XML(可扩展标记语言)和 HTML(超文本标记语言)是两种常见的标记语言,但它们有不同的目的和用途。它们都使用类似的标记结构(标签),但在设计上存在一些关键的差异。 XML…...

ubuntu服务器安装VASP.6.4.3
ubuntu服务器安装VASP.6.4.3 1 安装Intel OneAPI Base Toolkit和Intel OneAPI HPC Toolkit1.1 更新并安装环境变量1.2 下载Intel OneAPI Base Toolkit和Intel OneAPI HPC Toolkit安装包1.3 安装 Intel OneAPI Base Toolkit1.4 安装 Intel OneAPI HPC Toolkit1.5 添加并激活环境…...

市场加速下跌,但监管「坚冰」正在消融
作者:Techub 热点速递 撰文:Yangz,Techub News 与近日气温逐步回暖不同,自 2 月 25 日比特币跌破 9 万美元以来,加密货币市场行情一路下滑。今日 10 时 50 分左右,比特币更是跌破 8 万美元大关,…...

7.2 - 定时器之计算脉冲宽度实验
文章目录 1 实验任务2 系统框图3 软件设计 1 实验任务 本实验任务是通过CPU私有定时器来计算按键按下的时间长短。 2 系统框图 参见7.1。 3 软件设计 注意事项: 定时器是递减计数的,需要考虑StartCount<EndCount的情况。 /***********…...

Imagination DXTP GPU IP:加速游戏AI应用,全天候畅玩无阻
日前,Imagination 推出了最新产品——Imagination DXTP GPU IP,在智能手机和其他功耗受限设备上加速图形和AI工作负载时,保证全天候的电池续航。它是我们最新D系列GPU的最终产品,集成了自2022年发布以来引入的一系列功能ÿ…...

关于流水线的理解
还是不太理解,我之前一直以为,对axis总线,每一级的寄存器就像fifo一样,一级一级的分级存储最后一级需要的数据。(现在看来,我这个理解应该也是没有问题的) 如下图,一开始是在解析axi…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
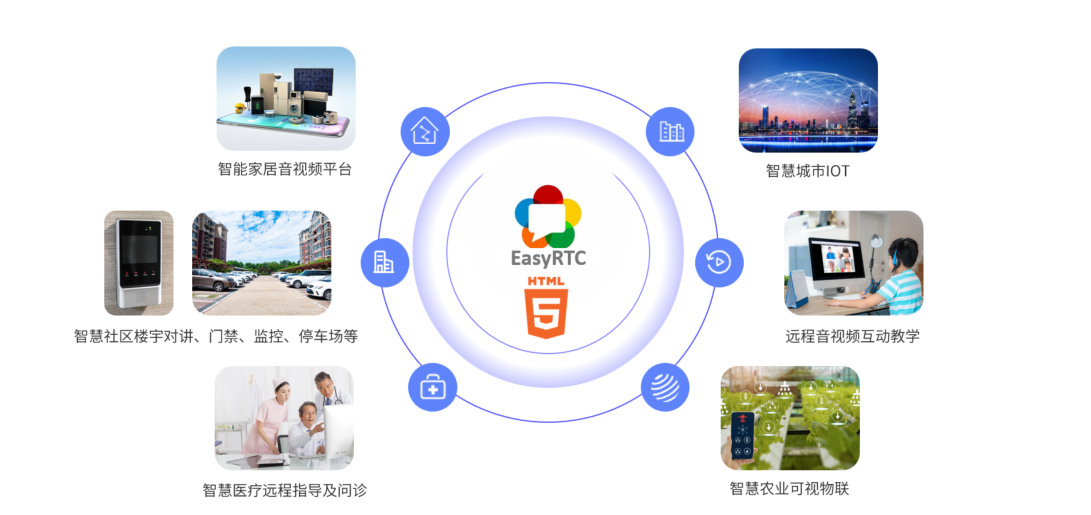
EasyRTC音视频实时通话功能在WebRTC与智能硬件整合中的应用与优势
一、WebRTC与智能硬件整合趋势 随着物联网和实时通信需求的爆发式增长,WebRTC作为开源实时通信技术,为浏览器与移动应用提供免插件的音视频通信能力,在智能硬件领域的融合应用已成必然趋势。智能硬件不再局限于单一功能,对实时…...
