水仙花数(华为OD)
题目描述
所谓水仙花数,是指一个n位的正整数,其各位数字的n次方和等于该数本身。
例如153是水仙花数,153是一个3位数,并且153 = 13 + 53 + 33。
输入描述
第一行输入一个整数n,表示一个n位的正整数。n在3到7之间,包含3和7。
第二行输入一个正整数m,表示需要返回第m个水仙花数。
输出描述
返回长度是n的第m个水仙花数。个数从0开始编号。
若m大于水仙花数的个数,返回最后一个水仙花数和m的乘积。
若输入不合法,返回-1。
运行结果

- 输入:4 1 输出:8208 说明:8208是第一个水仙花数
- 输入:7 5 输出:49631575 说明:5超出范围,所以最后一个水仙花数和5的乘积
- 输入:8 2 输出:49631575 说明:8超出范围
题目解析
本题的水仙花数最长有7位,这7位很少,我们可以直接提前计算好3~7位的所有水仙花数来配置为字典,进行打表查询,考试时怎么记得有哪些数字是水仙花数字呢,但是我已经写很简单的源码提供:
#include<stdio.h>
#include<math.h>
int main() {int x, y, z, a, b, c, d;int i;printf("3位数 -> 水仙花数分别为:");for (i = 100; i <= 999; i++) {x = i / 100;y = i / 10 % 10;z = i % 10;if (i == (int) pow(x, 3) + (int) pow(y, 3) + (int) pow(z, 3)) {printf("%d ", (int) pow(x, 3) + (int) pow(y, 3) + (int) pow(z, 3));}}printf("\n");printf("4位数 -> 水仙花数分别为:");for (i = 1000; i <= 9999; i++) {x = i / 1000;y = i / 100 % 10;z = i / 10 % 10;a = i % 10;if (i == (int) pow(x, 4) + (int) pow(y, 4) + (int) pow(z, 4) + (int) pow(a, 4)) {printf("%d ", (int) pow(x, 4) + (int) pow(y, 4) + (int) pow(z, 4) + (int) pow(a, 4));}}printf("\n");printf("5位数 -> 水仙花数分别为:");for (i = 12345; i <= 99999; i++) {x = i / 10000;y = i / 1000 % 10;z = i / 100 % 10;a = i / 10 % 10;b = i % 10;if (i == (int) pow(x, 5) + (int) pow(y, 5) + (int) pow(z, 5) + (int) pow(a, 5) + (int) pow(b, 5)) {printf("%d ", (int) pow(x, 5) + (int) pow(y, 5) + (int) pow(z, 5) + (int) pow(a, 5) + (int) pow(b, 5));}}printf("\n");printf("6位数 -> 水仙花数分别为:");for (i = 100000; i <= 999999; i++) {x = i / 100000;y = i / 10000 % 10;z = i / 1000 % 10;a = i / 100 % 10;b = i / 10 % 10;c = i % 10;if (i == (int) pow(x, 6) + (int) pow(y, 6) + (int) pow(z, 6) + (int) pow(a, 6) + (int) pow(b, 6) + (int) pow(c, 6)) {printf("%d ", (int) pow(x, 6) + (int) pow(y, 6) + (int) pow(z, 6) + (int) pow(a, 6) + (int) pow(b, 6) + (int) pow(c, 6));}}printf("\n");printf("7位数 -> 水仙花数分别为:");for (i = 1000000; i <= 9999999; i++) {x = i / 1000000;y = i / 100000 % 10;z = i / 10000 % 10;a = i / 1000 % 10;b = i / 100 % 10;c = i / 10 % 10;d = i % 10;if (i == (int) pow(x, 7) + (int) pow(y, 7) + (int) pow(z, 7) + (int) pow(a, 7) + (int) pow(b, 7) + (int) pow(c, 7) + (int) pow(d, 7)) {printf("%d ", (int) pow(x, 7) + (int) pow(y, 7) + (int) pow(z, 7) + (int) pow(a, 7) + (int) pow(b, 7) + (int) pow(c, 7) + (int) pow(d, 7));}}return 0;
}

我们可以看到所有水仙花数,直接复制进行打表法,这道题实现逻辑并不难,大家可以看下面算法源码
C算法源码
#include<stdio.h>
int main() {int n, m;scanf("%d", &n);scanf("%d", &m);if (3 <= n && 7 >= n && 0 <= m) {int daffodil[8][8];int daffodilSize[8];daffodil[3][0] = 153; daffodil[3][1] = 370; daffodil[3][2] = 371; daffodil[3][3] = 407;daffodilSize[3] = 4;daffodil[4][0] = 1634; daffodil[4][1] = 8208; daffodil[4][2] = 9474;daffodilSize[4] = 3;daffodil[5][0] = 54748; daffodil[5][1] = 92727; daffodil[5][2] = 93084;daffodilSize[5] = 3;daffodil[6][0] = 548834;daffodilSize[6] = 1;daffodil[7][0] = 1741725; daffodil[7][1] = 4210818; daffodil[7][2] = 9800817; daffodil[7][3] = 9926315;daffodilSize[7] = 4;if (m < daffodilSize[n]) {printf("%d", daffodil[n][m]);} else {printf("%lld", (long long) daffodil[n][daffodilSize[n] - 1] * m);}} else {printf("-1");}return 0;
}
相关文章:

水仙花数(华为OD)
题目描述 所谓水仙花数,是指一个n位的正整数,其各位数字的n次方和等于该数本身。 例如153是水仙花数,153是一个3位数,并且153 13 53 33。 输入描述 第一行输入一个整数n,表示一个n位的正整数。n在3到7之间&#x…...

【对话状态跟踪】关心整个对话过程用户完整意图变化
对话状态管理器 核心逻辑是解决键冲突和验证范围有效性, 但需依赖外部输入的正确性。在实际应用中, 可能需要结合用户提示或自动修正逻辑以提高鲁棒性。 NLU 槽 值 对儿 NLU的目的是把自然语言解析成结构化语义。结构化语义有多种表示方式,…...

【分享】网间数据摆渡系统,如何打破传输瓶颈,实现安全流转?
在数字化浪潮中,企业对数据安全愈发重视,网络隔离成为保护核心数据的重要手段。内外网隔离、办公网与研发网隔离等措施,虽为数据筑牢了防线,却也给数据传输带来了诸多难题。传统的数据传输方式在安全性、效率、管理等方面暴露出明…...

TikTok创作者市场关闭!全新平台TikTok One将带来哪些改变?
TikTok创作者市场关闭,全新平台TikTok One上线,创作者和品牌将迎来哪些新机遇? 近日,TikTok宣布关闭其原有的创作者市场(TikTok Creator Marketplace),并推出全新平台TikTok One。这一消息在社…...
LeetCode hot 100—矩阵置零
题目 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2࿱…...
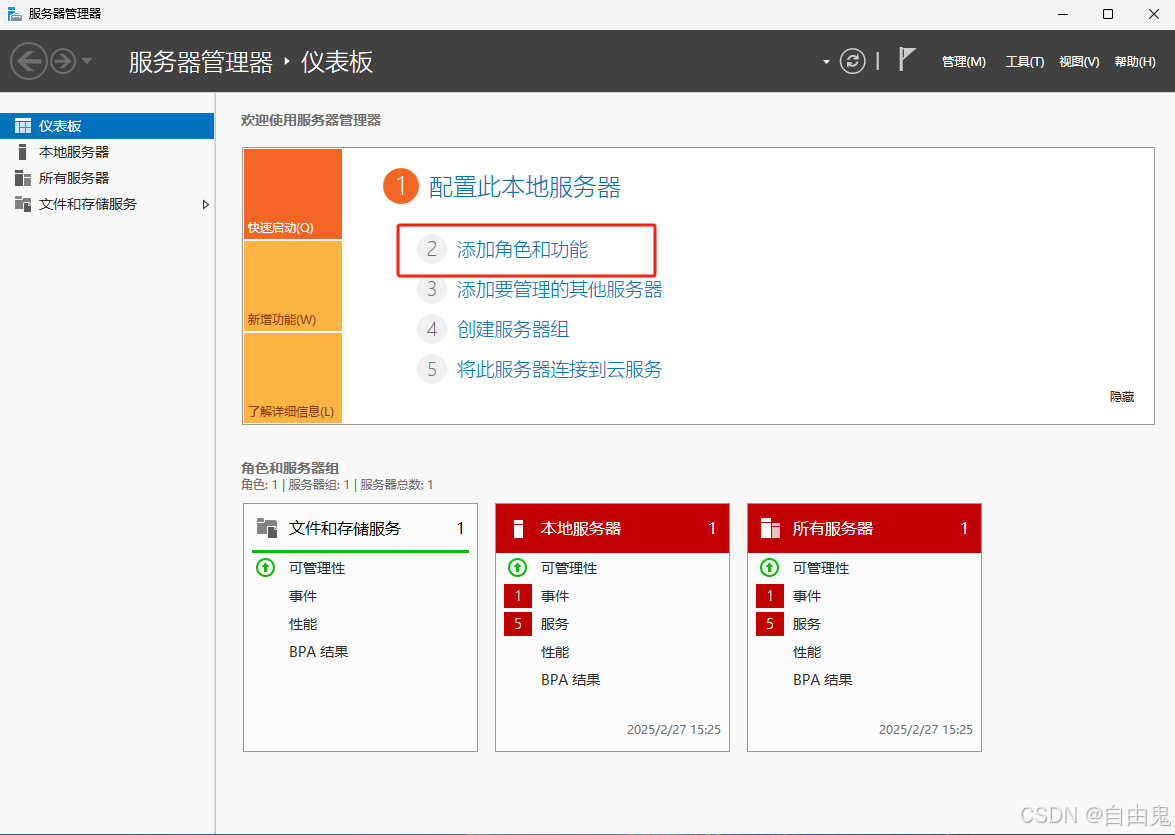
部署Windows Server自带“工作文件夹”实现企业网盘功能完整步骤
前文已经讲解过Windows Server自带的“工作文件夹”功能,现以Windows Server 2025为例介绍部署工作文件夹的完整步骤: 为了确保您能够顺利部署和充分利用工作文件夹的功能,我将按照以下步骤进行讲解。 请注意,在域环境中部署工作…...

植物大战僵尸杂交版v3.3最新版本(附下载链接)
B站游戏作者潜艇伟伟迷于12月21日更新了植物大战僵尸杂交版3.3版本!!!,有b站账户的记得要给作者三连关注一下呀! 不多废话下载链接放上: 夸克网盘链接::https://pan.quark.cn/s/6f2a…...

非关系型数据库和关系型数据库的区别
非关系型数据库(NoSQL)和关系型数据库(SQL)的主要区别体现在以下几个方面: 数据模型: 关系型数据库(SQL):数据以表格形式存储,数据行和列组成,每个…...

CPU负载高告警问题的定位与优化建议
#作者:猎人 文章目录 背景一.问题排查1.1 找到相应的容器1.2 找到对应的deployment1.3 查看pod日志1.4 查看nginx配置文件1.5 查看deployment的yaml文件 二.优化建议 背景 Docker 版本:19.03.14 Operating System: Red Hat Ent…...

2月28日,三极管测量,水利-51单片机
众所周知,三极管(BJT)有三个管脚,基极(B)、集电极(C)、发射极(E),在实际应用中,不可避免地会遇到引脚辨别的问题。接下来就讲下三极管…...

批量提取 Word 文档中的图片
在 Word 文档中,我们可以插入图片、文本、链接等各种各样的资源。在某些场景下我们需要提取这些信息,比如我们需要提取 Word 文档中的图片,将每一个 Word 文档中的图片都提取出来放到一个单独的文件夹中,那么我们应该怎么做呢&…...

C#—Settings配置详解
C#—Settings配置详解 在C#项目中,全局配置通常指的是应用程序的设置(settings),这些设置可以跨多个类或组件使用,并且通常用于存储应用程序的配置信息,如数据库连接字符串、用户偏好设置等。 Settings配置…...

UI自动化框架介绍
selenium Pytest Allure 优势 1.1 更高效的自动化测试 Selenium 提供了强大的浏览器自动化能力,可以模拟用户与网页的交互。它能够在不同浏览器上运行测试,确保 Web 应用程序在多种环境下的兼容性。Pytest 是一个非常灵活、简洁的 Python 测试框架&a…...

【工具推荐】在线提取PDF、文档、图片、论文中的公式
网址1:https://simpletex.cn/ai/latex_ocr 网址2: https://www.latexlive.com/home 推荐理由:无需下载,在线使用,直接 截图 CTRLV 效果更佳。...

帮我设计一个c语言学习阶段
以下是一个针对不同学习阶段的C语言学习计划,你可以根据自己的基础和目标进行调整: 第一阶段:基础语法与程序结构(第1-4周) 目标 熟悉C语言的基本语法和程序结构。 能够编写简单的程序。 学习内容 环境搭建 安装…...

解决windows npm无法下载electron包的问题
1.将nsis.zip解压到C:\Users\XXX\AppData\Local\electron-builder\Cache 2.将winCodeSign.zip解压到C:\Users\XXX\AppData\Local\electron-builder\Cache 3.将electron-v20.3.8-win32-ia32.zip复制到C:\Users\XXX\AppData\Local\electron\Cache 4.将electron-v20.3.8-win32-…...

网络编程 day01
网络编程 day01 0. 网络编程课程介绍1. 认识网络1.网络发展史2.局域网与广域网局域网(LAN)广域网(Wan) 3.光猫4.路由器5.交换机与路由器6.网线 2. IP1. 基本概念2. 网络号/主机号(二级划分)3. IP地址分类整…...

【三.大模型实战应用篇】【4.智能学员辅导系统:docx转PDF的自动化流程】
去年团队庆功宴上,我司CTO端着酒杯过来:“老王啊,咱们现在文档解析做得挺溜了,但老师们总抱怨下载的作业格式乱码…” 我看了眼手机里凌晨三点收到的崩溃警报,把杯里的可乐一饮而尽——得,新的副本又开了。 一、为什么PDF转换比想象中难十倍? 某次用户调研中,数学教研…...

2915. 和为目标值的最长子序列的长度
给你一个下标从 0 开始的整数数组 nums 和一个整数 target 。 返回和为 target 的 nums 子序列中,子序列 长度的最大值 。如果不存在和为 target 的子序列,返回 -1 。 子序列 指的是从原数组中删除一些或者不删除任何元素后,剩余元素保持原来…...

谷仓的安保
Farmer John给谷仓安装了一个新的安全系统,并且要给牛群中的每一个奶牛安排一个有效的密码。一个有效的密码由L(3 < L < 15)个小写字母(来自传统的拉丁字母集a...z)组成,至少有一个元音(a, e, i, o, 或者 u),至少两个辅音(除去元音以外…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

多模态大语言模型arxiv论文略读(112)
Assessing Modality Bias in Video Question Answering Benchmarks with Multimodal Large Language Models ➡️ 论文标题:Assessing Modality Bias in Video Question Answering Benchmarks with Multimodal Large Language Models ➡️ 论文作者:Jea…...
