有符号数和无符号数的加减运算
一、无符号数的加减运算
-
加法
- 规则:直接按二进制逐位相加,若最高位产生进位(即结果超出(2^n)范围),则结果对(2^n)取模((n)为位数)。
- 示例(8位无符号数):
- (200 + 100 = 300),但8位最大值为255,溢出后结果为(300 \mod 256 = 44)。
- 结果:(\boxed{44})
-
减法
- 规则:直接按二进制逐位相减,若被减数小于减数,结果回绕为(2^n - |被减数 - 减数|)。
- 示例(8位无符号数):
- (10 - 20 = -10),回绕后结果为(256 - 10 = 246)。
- 结果:(\boxed{246})
二、有符号数的加减运算(补码表示)
-
加法
- 规则:
- 直接按二进制逐位相加(符号位参与运算)。
- 溢出判断:若两个正数相加结果为负,或两个负数相加结果为正,则溢出。
- 示例(8位有符号数):
- (100 + 50 = 150)(8位有符号数范围为(-128)到(127)),溢出后结果为补码(10010110_2 = -106)。
- 结果:(\boxed{-106\quad(\text{溢出})})
- 规则:
-
减法
- 规则:将减法转换为加法,即(A - B = A + (-B)),其中(-B)为(B)的补码(取反后加1)。
- 示例(8位有符号数):
- (50 - 100 = 50 + (-100)):
- (100)的补码:取反(01100100_2 \rightarrow 10011011_2),加1得(10011100_2)(即(-100))。
- 计算(00110010_2 + 10011100_2 = 11001110_2)(补码),对应十进制(-50)。
- 结果:(\boxed{-50})
- (50 - 100 = 50 + (-100)):
三、溢出检测
-
无符号数:
- 加法溢出:最高位产生进位(进位标志位为1)。
- 减法溢出:被减数小于减数(借位标志位为1)。
-
有符号数:
- 加法溢出:两正数相加得负,或两负数相加得正。
- 减法溢出:正数减负数得负,或负数减正数得正。
四、关键区别
| 运算类型 | 无符号数 | 有符号数(补码) |
|---|---|---|
| 表示范围 | (0 \leq x < 2^n) | (-2^{n-1} \leq x < 2^{n-1}) |
| 溢出处理 | 结果对(2^n)取模 | 符号位异常(需检测溢出) |
| 减法实现 | 直接二进制减法 | 转换为加法((A + (-B))) |
五、常见问题
-
为什么有符号数用补码表示?
- 补码统一了正负数的加减法规则,符号位可直接参与运算,无需额外判断。
-
如何快速计算补码?
- 对原码取反(按位取反)后加1。例如:
(100_{10} = 01100100_2 \rightarrow 10011011_2 + 1 = 10011100_2)(即(-100))。
- 对原码取反(按位取反)后加1。例如:
-
如何判断结果是否溢出?
- 无符号数:观察进位/借位标志位。
- 有符号数:检查符号位是否异常(如正+正=负)。
通过上述规则和示例,可以清晰理解无符号数和有符号数在加减运算中的差异及处理逻辑。
相关文章:

有符号数和无符号数的加减运算
一、无符号数的加减运算 加法 规则:直接按二进制逐位相加,若最高位产生进位(即结果超出(2^n)范围),则结果对(2^n)取模((n)为位数)。示例(8位无符号数): (200 …...
动态链接器(十):重定位
ELF文件中有许多种类型的重定位条目,这些重定位条目指导动态链接器在加载或运行时解析符号地址,确保程序能够正确地引用动态库中的函数和变量。 本文主要介绍那些与动态链接有关的重定位条目(主要介绍Rela相关的,Rel相关的不作介…...

EGO-Planner的无人机视觉选择(yolov5和yolov8)
EGO-Planner的无人机视觉选择(yolov5和yolov8) 效果 yolov5检测效果 yolov8检测效果 一、YOLOv8 vs YOLOv5:关键差异解析 1. 训练效率:为何YOLOv8更快? 架构轻量化 YOLOv8采用C2f模块(Cross Stage Partia…...
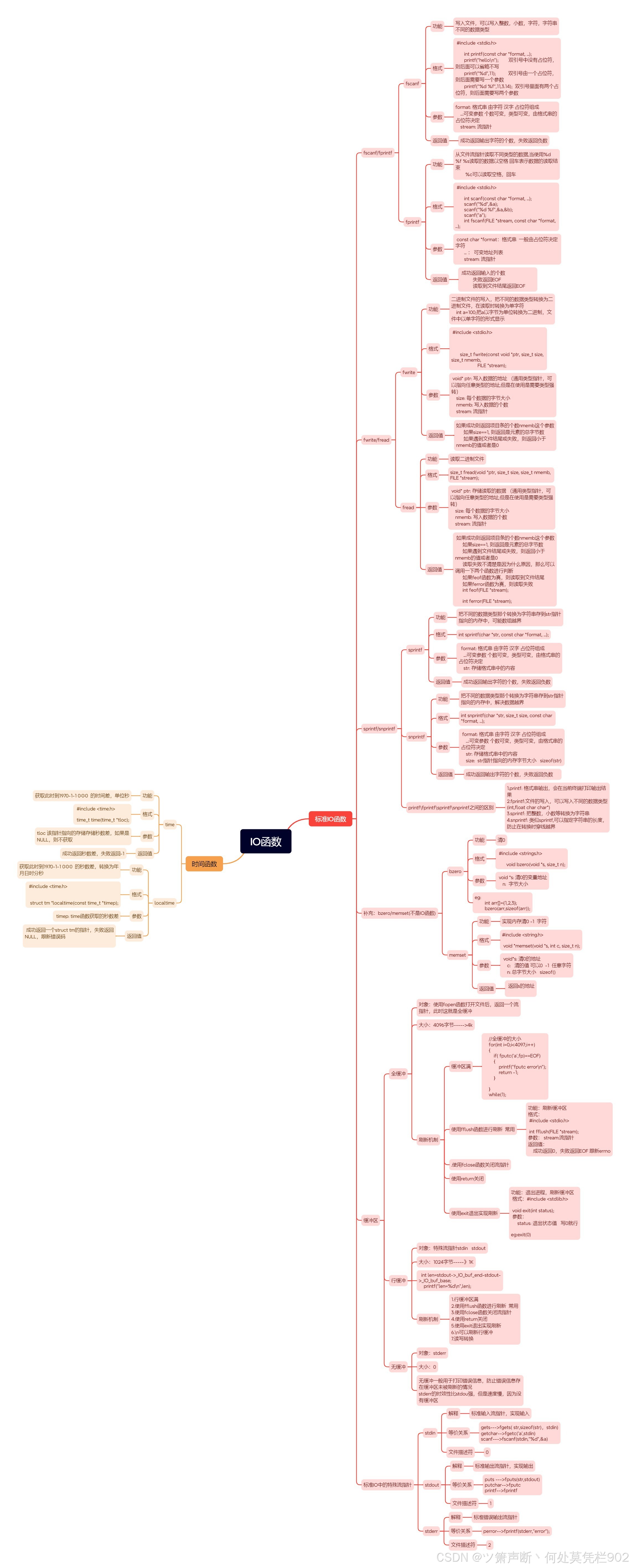
IO标准函数和时间函数
1、将当前的时间写入到time. txt的文件中,如果ctrlc退出之后,在再次执行支持断点续写 1.2022-04-26 19:10:20 2.2022-04-26 19:10:21 3.2022-04-26 19:10:22 //按下ctrlc停止,再次执行程序 4.2022-04-26 20:00:00 5.2022-04-26 20:00:0…...

为AI聊天工具添加一个知识系统 之133 详细设计之74通用编程语言 之4 架构及其核心
本篇继续讨论 通用编程语言。 说明:本阶段的所有讨论都是围绕这一主题展开的,但前面的讨论分成了三个大部分(后面列出了这一段的讨论题目的归属关系)-区别distinguish(各别): 文化和习俗。知识…...

【零基础到精通Java合集】第二十三集:G1收集器深度解析
课程标题:G1收集器深度解析——面向大内存与低延迟的现代垃圾回收器(15分钟) 目标:掌握G1核心设计思想、运行机制与调优策略,理解其如何平衡吞吐量与低延迟 0-1分钟:课程引入与G1设计目标 以“城市交通智能调度”类比G1核心思想:将堆内存划分为多个区域(Region),动…...

似然函数与极大似然估计
前言 本文隶属于专栏《机器学习数学通关指南》,该专栏为笔者原创,引用请注明来源,不足和错误之处请在评论区帮忙指出,谢谢! 本专栏目录结构和参考文献请见《机器学习数学通关指南》 正文 📚 1. 似然函数&a…...
详解)
QSFP(Quad Small Form-factor Pluggable)详解
1. QSFP的定义 QSFP(Quad Small Form-factor Pluggable)是一种四通道热插拔光模块/电模块,专为高速网络传输设计。其名称中的“Quad”表示模块集成4个独立通道,每个通道支持1Gbps至10Gbps速率(总带宽可达40Gbps&#…...

WDM_OTN_基础知识_波分系统基本构成-无源器件
在波分系统中通常将发光,对光进行放大以及产生光电转换的器件称之为有源器件,例如光放,激光器,与此相反,将那些不发光,不对光进行放大,也不产生光电转换的器件称之为无源器件,波分系统中的无源器…...

【音视频】ffmpeg音视频处理基本流程
一、ffmpeg音视频处理基本流程 首先先看两条命令 ffmpeg -i 1.mp4 -acodec copy -vcodec libx264 -s 1280x720 2.flv ffmpeg -i 1.mp4 -acodec copy -vcodec libx265 -s 1280x720 3.mkv-i :表示输入源,这里是1.mp4,是当前路径下的视频文件-acodec copy…...

【网络编程】之TCP实现客户端远程控制服务器端及断线重连
【网络编程】之TCP实现客户端远程控制服务器端及断线重连 TCP网络通信实现客户端简单远程控制主机基本功能演示通信过程代码实现服务器模块执行命令模块popen系列函数 客户端模块服务器主程序 windows作为客户端与服务器通信#pragma comment介绍 客户端使用状态机断线重连代码实…...

云原生容器编排:构建智能弹性应用的自动化引擎
引言:重构应用部署范式 Google Borg系统管理着超2500万容器实例,每日处理200亿个任务。阿里巴巴双十一使用Kubernetes实现300万Pod秒级弹性,资源利用率达65%。CNCF 2023报告显示全球Kubernetes生产采用率突破92%,CRI-O容器启动速…...

centos虚拟机安装
以下是一个详细的 VMware CentOS 虚拟机安装教程,结合了最新的信息和步骤: 一、准备工作 1. 下载 VMware 软件 访问 VMware 官方网站:VMware Workstation 官网。点击“现在安装”并下载适合您操作系统的 VMware Workstation。 2. 下载 Ce…...

社会力模型:Social force model for pedestrian dynamics
Social Force Model——社会力模型-CSDN博客 简介: 时间:1995 期刊:《Physical Review E》 作者:Dirk Helbing and Peter Molnar 摘要: 提出一种描述行人运动的“社会力模型”。认为行人的运动可看作是受到一系列…...

机器学习数学通关指南
✨ 写在前面 💡 在代码的世界里沉浸了十余载,我一直自诩逻辑思维敏捷,编程能力不俗。然而,当我初次接触 DeepSeek-R1 并领略其清晰、系统的思考过程时,我不禁为之震撼。那一刻,我深刻意识到:在A…...

【Mac】2025-MacOS系统下常用的开发环境配置
早期版本的一个环境搭建参考 1、brew Mac自带终端运行: /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)" Installation successful!成功后运行三行命令后更新环境(xxx是mac的username&a…...
与栈(Stack)的区别)
# C# 中堆(Heap)与栈(Stack)的区别
在 C# 中,堆和栈是两种不同的内存分配机制,它们在存储位置、生命周期、性能和用途上存在显著差异。理解堆和栈的区别对于优化代码性能和内存管理至关重要。 1. 栈(Stack) 1.1 定义 栈是一种后进先出(LIFO࿰…...

ubuntu离线安装nvidia-container-runtime
参考文章 ubuntu系统docker20.4版本安装nvidia-container-runtime3.11.0-1版本(离线安装nvidia-docker) - jokerMM - 博客园 https://zhuanlan.zhihu.com/p/15194336245 一、软件地址 Index of /nvidia-docker/libnvidia-container/stable/ 从上述地地址——进入对应系统—…...

用Python+Flask打造可视化武侠人物关系图生成器:从零到一的实战全记录
用PythonFlask打造可视化武侠人物关系图生成器:从零到一的实战全记录 一、缘起:一个程序小白的奇妙探索之旅 作为一个接触Python仅13天的编程萌新,我曾以为开发一个完整的应用是遥不可及的事情。但在DeepSeek的帮助下,我竟用短短…...

学习笔记-DeepSeek在开源第四天发布DualPipe和EPLB两项技术
在AI模型训练的进程中,优化并行策略对于提升训练效率和资源利用率至关重要。DeepSeek在开源周第四天发布的DualPipe和EPLB两项技术,为V3/R1训练场景下的并行优化提供了创新解决方案。 DualPipe:双向管道并行算法 技术原理: Dua…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
