动态规划/贪心算法
一、动态规划
动态规划 是一种用于解决优化问题的算法设计技术,尤其适用于具有重叠子问题和最优子结构性质的问题。它通过将复杂问题分解为更简单的子问题,并保存这些子问题的解以避免重复计算,从而提高效率。
动态规划的核心思想
-
最优子结构(Optimal Substructure):
- 一个问题的最优解可以通过其子问题的最优解来构造。
- 比如在最短路径问题中,从起点到终点的最短路径可以由起点到某个中间点的最短路径和该中间点到终点的最短路径组合而成。
-
重叠子问题(Overlapping Subproblems):
- 在递归求解过程中,相同的子问题会被多次求解。
- 动态规划通过存储子问题的解来避免重复计算,通常使用数组或哈希表等数据结构来存储这些解。
1.算法原理
1)状态表示
dp表(一维数组 填满该表其中某一个值就是结果 数组中某个数据值的意义就是状态表示)
通过题目要求 经验 分析问题发现重复子问题 来创建dp表
2)状态转移方程
dp[i]等于什么?
3)初始化
根据状态转移方程填表,保证填表的时候不越界
4)填表顺序
为了填写当前状态的时候,所需要的状态已经计算过了
5)返回值
题目要求+状态表示
2.例题
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:输入:n = 4 输出:4 解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4
状态表示:dp[i]第i个泰波那契数的值
状态转移方程:dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
初始化:dp[0]=0;dp[1]=1;dp[2]=1
填表顺序:从左向右
返回值:dp[n]
JAVA代码
class Solution {public int tribonacci(int n) {
if(n==0) return 0;
if(n==1||n==2) return 1;
int[] dp=new int[n+1];
dp[0]=0;dp[1]=1;dp[2]=1;
for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
}
return dp[n];}
}3.空间优化
求解某个状态时仅需要其的前几个状态
一定要确定好赋序
int tribonacci(int n){
//空间优化 滚动数组
if(n==0) return 0;
if(n==1||n==2) return 1;
int a=0;int b=1,c=1;int d=0;
for(int i=3;i<=n;i++){d=a+b+c;a=b;b=c;c=d;}
return d;
}

二、贪心算法
1.算法原理:
局部最优->全局最优
把解决问题的过程分为若干步,解决每一步的时候都选择当前看起来最优的解法
希望得到全局最优解
但贪心算法并不总是保证全局最优解
2.例题
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
示例 1:
[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
在数组中挑出两个数,使其差值最大
1)暴力解法(两层for循环) 超出时间限制时间复杂度O(n^2)
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;class Solution {public int maxProfit(int[] prices) {int ret = 0;if (prices == null || prices.length < 2) {return 0;}for (int i = 0; i < prices.length - 1; i++) {for (int j = i+1; j < prices.length; j++) {ret = Math.max(ret, prices[j] - prices[i]);}}return ret;}public static void main(String[] args) {Scanner sc=new Scanner(System.in);Solution solution=new Solution();List<Integer> pricesList = new ArrayList<>();while (sc.hasNextInt()) {pricesList.add(sc.nextInt());}int[] prices = new int[pricesList.size()];for (int i = 0; i < pricesList.size(); i++) {prices[i] = pricesList.get(i);}int ret=solution.maxProfit(prices);System.out.println(ret);sc.close();}
}//在输入结束后输入一个非数字字符(如字母 'q'),这样 hasNextInt() 会返回 false,从而结束循环,或 Ctrl + Z(Windows)来发送 EOF 信号。2)贪心
分为两段,prevmin表示前一段中最小值(买入),prices[i]卖出去的价钱
class Solution {public int maxProfit(int[] prices) {int ret=0;for(int i=0,prevmin=Integer.MAX_VALUE;i<prices.length;i++){ret=Math.max(ret,prices[i]-prevmin);prevmin=Math.min(prevmin,prices[i]);}return ret;}
}三、 (双指针算法)
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums =[0,1,0,3,12]输出:[1,3,12,0,0]
数组划分
利用数组下标充当指针
两个指针的作用:
cur:从左往右扫描,遍历数组
dest:已处理的区间内,非0元素的最后一个位置
三个区间:
[0,dest] [dest+1,cur-1] [cur,n-1]
非0 0元素 待处理的区间
解法:
初始dest=-1 cur=0
遇到0元素,cur++;
遇到非0元素 swap(dest+1,cur)交换位置 dest++ cur++

class Solution {public void moveZeroes(int[] nums) {
int dest=-1;
int cur=0;
int k=0;
int n=nums.length;
while(cur<n){
if(nums[cur]==0)
cur++;
else
{dest++;
k=nums[dest];
nums[dest]=nums[cur];
nums[cur]=k;
cur++;
}}}
}
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
输入:prices = [7,1,5,3,6,4] 输出:7 解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。 随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。 最大总利润为 4 + 3 = 7 。
利用数组下标充当指针(i,j)
class Solution {public int maxProfit(int[] prices) {//双指针算法int ret=0;int i=0,j=0;for(i=0;i<prices.length;i++){j=i;while(j+1<prices.length && prices[j+1]-prices[j]>0){j++;}ret+=prices[j]-prices[i];i=j;}return ret;}
}四、递归
1.什么是递归
函数自己调用自己(主问题->相同的子问题)
出口(一个问题不能在分割了)
1.算法思想
函数头 函数体 递归出口
把递归的函数当成一个黑盒,不在意递归的细节
深度优先遍历(后序遍历)
2.例题
计算布尔二叉树的值
给你一棵 完整二叉树 的根,这棵树有以下特征:
- 叶子节点 要么值为
0要么值为1,其中0表示False,1表示True。 - 非叶子节点 要么值为
2要么值为3,其中2表示逻辑或OR,3表示逻辑与AND。
计算 一个节点的值方式如下:
- 如果节点是个叶子节点,那么节点的 值 为它本身,即
True或者False。 - 否则,计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
class Solution {public boolean evaluateTree(TreeNode root) {if(root.left==null) return root.val==0 ? false: true;boolean left=evaluateTree(root.left);boolean right=evaluateTree(root.right);return root.val==2 ?left | right : left & right;}
}相关文章:

动态规划/贪心算法
一、动态规划 动态规划 是一种用于解决优化问题的算法设计技术,尤其适用于具有重叠子问题和最优子结构性质的问题。它通过将复杂问题分解为更简单的子问题,并保存这些子问题的解以避免重复计算,从而提高效率。 动态规划的核心思想 最优子结…...

PH热榜 | 2025-03-04
1. MGX 标语:第一支人工智能开发团队 介绍:MGX(MetaGPT X)是一个基于真实软件标准操作程序(SOP)的多代理人工智能平台。在这里,你可以随时与AI团队的领导、产品经理、架构师、工程师和数据分析…...

Mybatis-Plus 插件机制与自定义插件实现
1. Mybatis-Plus 插件系统概述 Mybatis-Plus 提供了一个简单而强大的插件机制,允许开发者在 MyBatis 执行 SQL 的过程中插入自定义逻辑。通过插件机制,用户可以实现对 SQL 执行过程的拦截和修改。Mybatis-Plus 插件基于 MyBatis 的拦截器模式进行实现&a…...

开源表单、投票、测评平台部署教程
填鸭表单联合宝塔面板深度定制,自宝塔面板 9.2 版本开始,在宝塔面板-软件商店中可以一键部署填鸭表单系统。 简单操作即可拥有属于自己的表单问卷系统,快速赋能业务。即使小白用户也能轻松上手。 社区版体验地址:https://demo.tduckapp.com/home 前端项目地址: tduck-fro…...

行为模式---命令模式
概念 命令模式是一种行为设计模式,它的核心思想就是将请求封装为一个对象,此对象包含与请求相关的所有信息。可以用不同的请求对客户进行参数化。命令模式通过将请求的发送者和接收者解耦,支持请求的排队、记录、撤销等操作。 使用场景 1、…...

zabbix配置邮件告警
目录 实现步骤: 实现目的: 1.在监控端操作: 2.web界面部署 实现步骤: 1、在 zabbix服务端配置邮件发送脚本和修改 zabbix服务端配置文件; 2、在 zabbix前端控制台进行相关设置。 实现目的: Zab…...

INI和CSV文件保存
INI文件 INI文件是一种配置文件格式,通常用于Windows操作系统中的应用程序中。 它是一种文本文件,由多个节和键值对组成,用于存储应用程序的配置信息。 INI文件的特点包括: INI文件是一种文本文件,易于编辑和阅读。…...

汽车智能钥匙中PKE低频天线的作用
PKE(Passive Keyless Entry)即被动式无钥匙进入系统,汽车智能钥匙中PKE低频天线在现代汽车的智能功能和安全保障方面发挥着关键作用,以下是其具体作用: 信号交互与身份认证 低频信号接收:当车主靠近车辆时…...

计算机等级考试
一、计算机等级考试——题库 (1)选择题 (2)基本操作题 (3)上网题 (4)文字题 (5)表格题 (6)演示文稿题 二、计算机等级考试——标准评…...

Geotools中获取Shapefile的属性表格字符集编码的一种方法
目录 前言 1、字符集编码的重要性 2、Geotools 在 GIS 开发中的地位 一、GeoTools的字符集知识 1、字符集的作用 2、shapefile中字符集信息 二、GeoTools中获取字符集的方法 1、默认获取 2、从DataStore中获取 3、从CPG文件中获取 4、生产字符获取实践 三、总结 前言…...

HTTP 与 HTTPS 协议:从基础到安全强化
引言 互联网的消息是如何传递的? 是在路由器上不断进行跳转 IP的目的是在寻址 HTTP 协议:互联网的基石 定义 HTTP(英文:HyperText Transfer Protocol,缩写:HTTP),即超文本传输协…...

Scrapy爬虫框架介绍
目录 什么是Scrapy Scrapy核心组件 Scrapy扩展组件 组件交互流程 安装Scrapy Scrapy项目目录结构说明 创建Scrapy项目 创建爬虫 运行爬虫 配置请求头 全局配置请求头 指定爬虫配置请求头 配置管道pipeline 全局配置pipeline 方式一:指定爬虫配置pipe…...

Stable Diffusion模型高清算法模型类详解
Stable Diffusion模型高清算法模型类详细对比表 模型名称核心原理适用场景参数建议显存消耗细节增强度优缺点4x-UltraSharp残差密集块(RDB)结构优化纹理生成真实人像/建筑摄影重绘幅度0.3-0.4,分块尺寸768px★★★★★☆皮肤纹理细腻,但高对比场景易出现…...

软考网络安全口诀
首先,我们来看第一个口诀 “防御为先,安全无小事”。这个口诀强调了网络安全中的防御意识。在软考备考过程中,我们需要深刻理解网络安全不仅仅是技术层面的问题,更是一种全面的防御思维。从网络架构设计到日常运维管理࿰…...

Baklib内容中台赋能企业智管
内容中台构建全场景智管 现代企业数字化运营中,全域内容管理能力已成为核心竞争力。通过智能知识引擎驱动的内容中台架构,企业能够实现跨部门、多形态数据的统一归集与动态调度。以某制造企业为例,其利用中台系统将分散在CRM、ERP及内部文档…...

vscode+vue前端开发环境配置
目录 一、安装Vue二、使用vue新建项目 一、安装Vue 在node.js安装好之后, npm config set registry https://registry.npmmirror.com# 安装vue相关工具,webpack用来项目构建、打包、资源整合等。 npm install webpack -g# 安装vue-cli脚手架 npm insta…...

Python项目-基于深度学习的校园人脸识别考勤系统
引言 随着人工智能技术的快速发展,深度学习在计算机视觉领域的应用日益广泛。人脸识别作为其中的一个重要分支,已经在安防、金融、教育等多个领域展现出巨大的应用价值。本文将详细介绍如何使用Python和深度学习技术构建一个校园人脸识别考勤系统&#…...
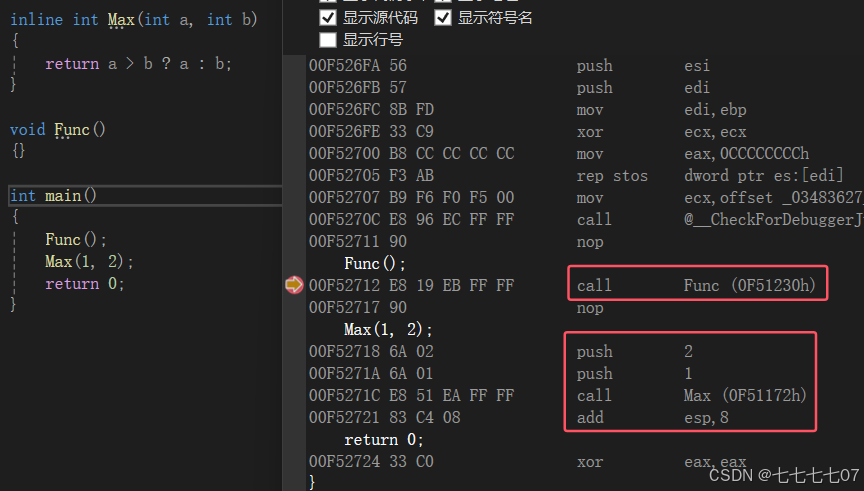
浅谈C++函数特性
C的函数特性 前言 在C中,函数加入了许多特性,例如:a、函数缺省参数 b、函数重载 c、内联函数 等等……,这里我会和大家详细去探讨这些特性。以及探讨这些特性的一些细节,同时在内联部分,我们还会把C语言的…...

Python----数据分析(Matplotlib三:绘图二:箱图,散点图,饼图,热力图,3D图)
一、箱图 箱图(Box Plot),又称为箱形图、箱线图、盒式图、盒状图或盒须图,是一种用于展示数据分布情况的统计图表 箱图通过显示数据的中位数、上下四分位数(Q1和Q3)、异常值和数据的分布范围,提…...

高性能PHP框架webman爬虫引擎插件,如何爬取数据
文章精选推荐 1 JetBrains Ai assistant 编程工具让你的工作效率翻倍 2 Extra Icons:JetBrains IDE的图标增强神器 3 IDEA插件推荐-SequenceDiagram,自动生成时序图 4 BashSupport Pro 这个ides插件主要是用来干嘛的 ? 5 IDEA必装的插件&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
