7.2 奇异值分解的基与矩阵
一、奇异值分解
奇异值分解(SVD)是线性代数的高光时刻。 A A A 是一个 m × n m\times n m×n 的矩阵,可以是方阵或者长方形矩阵,秩为 r r r。我们要对角化 A A A,但并不是把它化成 X − 1 A X X^{-1}A X X−1AX 的形式。这是因为 X X X 中的特征向量有三个大问题:它们通常并不正交,并不总是有足够数量的特征向量,并且 A x = λ x A\boldsymbol x=\lambda\boldsymbol x Ax=λx 要求 A A A 是方阵。 A A A 的奇异值向量(Singular vectors)完美的解决了这些问题。
由 SVD 我们可以得到:四个基本子空间合适的基。下面是按照基向量的重要性顺序,来求得这些基向量的步骤。
我们需要有两组奇异值向量 u i \boldsymbol u_i ui 和 v i \boldsymbol v_i vi,其中 u i \boldsymbol u_i ui 在 R m \pmb {\textrm R}^m Rm 中, v i \boldsymbol v_i vi 在 R n \textrm{\pmb R}^n Rn 中,它们将分别是 m × m m\times m m×m 的矩阵 U \pmb U U 和 n × n n\times n n×n 的矩阵 V \pmb V V 的列。下面会先根据这些基向量来描述 SVD,然后再根据正交矩阵 U U U 和 V V V 来描述 SVD。其基本思想是,在行空间中找到一组基标准交向量 v i \boldsymbol v_i vi,然后通过 A v i = σ i u i A\boldsymbol v_i=\sigma_i\boldsymbol u_i Avi=σiui 映射到列空间中的 u i \boldsymbol u_i ui,我们的目标是 v i \boldsymbol v_i vi 是特殊的标准正交向量,映射到 u i \boldsymbol u_i ui 也是标准正交。
(向量角度) u i \boldsymbol u_i ui 和 v j \boldsymbol v_j vj 给出了 A A A 的四个基本子空间的基:
u 1 , u 2 , ⋯ , u r 是 列空间 的标准正交基 u r + 1 , u r + 2 , ⋯ , u m 是 左零空间 N ( A T ) 的标准正交基 v 1 , v 2 , ⋯ , v r 是 行空间 的标准正交基 v r + 1 , v r + 2 , ⋯ , v n 是 零空间 N ( A ) 的标准正交基 \begin{array}{ll}\boldsymbol u_1,\boldsymbol u_2,\cdots,\boldsymbol u_r&是\pmb{列空间}的标准正交基\\\boldsymbol u_{r+1},\boldsymbol u_{r+2},\cdots,\boldsymbol u_m&是\pmb{左零空间\,N(A^T)\,}的标准正交基\\\boldsymbol v_1,\boldsymbol v_2,\cdots,\boldsymbol v_r&是\pmb{行空间}的标准正交基\\\boldsymbol v_{r+1},\boldsymbol v_{r+2},\cdots,\boldsymbol v_n&是\pmb{零空间}\,N(A)\,的标准正交基\end{array} u1,u2,⋯,urur+1,ur+2,⋯,umv1,v2,⋯,vrvr+1,vr+2,⋯,vn是列空间的标准正交基是左零空间N(AT)的标准正交基是行空间的标准正交基是零空间N(A)的标准正交基
这些基向量不仅正交,而且可以对角化矩阵 A A A:
“对角化 A \pmb A A” \kern 20pt A v 1 = σ 1 u 1 , A v 2 = σ 2 u 2 , ⋯ , A v r = σ r u r ( 7.2.1 ) {\color{blue}A\boldsymbol v_1=\sigma_1\boldsymbol u_1,\kern 5ptA\boldsymbol v_2=\sigma_2\boldsymbol u_2,\kern 5pt\cdots,\kern 5ptA\boldsymbol v_r=\sigma_r\boldsymbol u_r}\kern 20pt(7.2.1) Av1=σ1u1,Av2=σ2u2,⋯,Avr=σrur(7.2.1)
这些奇异值 σ 1 , σ 2 , ⋯ , σ r \pmb{\sigma_1,\sigma_2,\cdots,\sigma_r} σ1,σ2,⋯,σr 都是正数, σ i \sigma_i σi 是 A v i A\boldsymbol v_i Avi 的长度。对角矩阵 Σ \Sigma Σ 的对角元素除了奇异值 σ i \sigma_i σi 外都是零。
(矩阵角度)由于 u i \boldsymbol u_i ui 是标准正交的,所以由 r r r 个列向量组成的矩阵 U r U_r Ur 有 U r T U r = I U_r^TU_r=I UrTUr=I,而 v i \boldsymbol v_i vi 也是标准正交的,所以矩阵 V r V_r Vr 有 V r T V r = I V_r^TV_r=I VrTVr=I。则由方程 A v i = σ i u i A\boldsymbol v_i=\sigma_i\boldsymbol u_i Avi=σiui 推出 A V r = U r Σ r \pmb{AV_r=U_r\Sigma_r} AVr=UrΣr 的各列成立: ( m × n ) ( n × r ) A V r = U r Σ r ( m × r ) ( r × r ) A [ v 1 v 2 ⋯ v r ] = [ u 1 u 2 ⋯ u r ] [ σ 1 σ 2 ⋱ σ r ] ( 7.2.2 ) \begin{array}{l}(m\times n)(n\times r)\\\pmb{AV_r=U_r\Sigma_r}\\(m\times r)(r\times r)\end{array}\kern 10ptA\begin{bmatrix}\boldsymbol v_1&\boldsymbol v_2&\cdots&\boldsymbol v_r\end{bmatrix}=\begin{bmatrix}\boldsymbol u_1&\boldsymbol u_2&\cdots&\boldsymbol u_r\end{bmatrix}\begin{bmatrix}\sigma_1\\&\sigma_2\\&&\ddots\\&&&\sigma_r\end{bmatrix}\kern 15pt(7.2.2) (m×n)(n×r)AVr=UrΣr(m×r)(r×r)A[v1v2⋯vr]=[u1u2⋯ur] σ1σ2⋱σr (7.2.2)这个是 SVD 的核心,但是 SVD 并不是只有这些内容。这些 v i \boldsymbol v_i vi 和 u i \boldsymbol u_i ui 可以生成 A A A 的行空间和列空间,还可以从零空间 N ( A ) \pmb N(A) N(A) 和左零空间 N ( A T ) \pmb N(A^T) N(AT) 得到 n − r n-r n−r 个 v j \boldsymbol v_j vj 和 m − r m-r m−r 个 u i \boldsymbol u_i ui,它们也和前面的 v i \boldsymbol v_i vi 和 u i \boldsymbol u_i ui 正交(这是因为四个基本子空间配对正交)。我们现在在 V V V 和 U U U 中包含所有的 v j \boldsymbol v_j vj 和 u i \boldsymbol u_i ui,这两个矩阵就变成了方阵,仍然有 A V = U Σ \pmb{AV=U\Sigma} AV=UΣ。 ( m × n ) ( n × n ) A V = U Σ ( m × m ) ( m × n ) A [ v 1 ⋯ v r ⋯ v n ] = [ u 1 ⋯ u r ⋯ u m ] [ σ 1 σ 2 ⋱ σ r ] ( 7.2.3 ) \begin{array}{l}(m\times n)(n\times n)\\\pmb{AV=U\Sigma}\\(m\times m)(m\times n)\end{array}\kern 10ptA\begin{bmatrix}\boldsymbol v_1&\cdots&\boldsymbol v_r&\cdots&\boldsymbol v_n\end{bmatrix}=\begin{bmatrix}\boldsymbol u_1&\cdots&\boldsymbol u_r&\cdots&\boldsymbol u_m\end{bmatrix}\begin{bmatrix}\sigma_1\\&\sigma_2\\&&\ddots\\&&&\sigma_r\\&\end{bmatrix}\kern 15pt(7.2.3) (m×n)(n×n)AV=UΣ(m×m)(m×n)A[v1⋯vr⋯vn]=[u1⋯ur⋯um] σ1σ2⋱σr (7.2.3)新的 Σ \Sigma Σ 是 m × n m\times n m×n 的矩阵,它是(7.3.2)中的 r × r r\times r r×r 矩阵下面添加 m − r m-r m−r 个零行,右侧添加 n − r n-r n−r 个零列。真正的变化是 U U U 和 V V V 的形状,它们变成了方阵,并且有 V − 1 = V T V^{-1}=V^T V−1=VT,所以 A V = U Σ AV=U\Sigma AV=UΣ 就变成了 A = U Σ V T \pmb{A=U\Sigma V^T} A=UΣVT,这个就是奇异值分解(Singular Value Decompositon),可以用 U Σ U\Sigma UΣ 中的列 u i σ i \boldsymbol u_i\sigma_i uiσi 乘上 V T V^T VT 的行:
SVD A = U Σ V T = u 1 σ 1 v 1 T + u 2 σ 2 v 2 T + ⋯ + u r σ r v r T ( 7.2.4 ) \kern 30pt{\color{blue}A=U\Sigma V^T=\boldsymbol u_1\sigma_1\boldsymbol v_1^T+\boldsymbol u_2\sigma_2\boldsymbol v_2^T+\cdots+\boldsymbol u_r\sigma_r\boldsymbol v_r^T}\kern 20pt(7.2.4) A=UΣVT=u1σ1v1T+u2σ2v2T+⋯+urσrvrT(7.2.4)
式(7.3.2)是 “缩略版的 SVD(reduced SVD)”,它只包含行空间和列空间的基,式(7.3.3)是完整版的 SVD,它将零空间的基也包含了进去。这两个式子都是将 A A A 分解成同样的 r r r 个秩一矩阵 u i σ r v i T \boldsymbol u_i\sigma_r\boldsymbol v_i^T uiσrviT 的和。列乘行是矩阵乘法的第四种方式。
我们后面能够看到每个 σ i 2 \sigma_i^2 σi2 既是 A T A A^TA ATA 的特征值,也是 A A T AA^T AAT 的特征值。我们将奇异值按照降序排列: σ 1 ≥ σ 2 ≥ ⋯ ≥ σ r > 0 \sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r>0 σ1≥σ2≥⋯≥σr>0,式(7.2.4)中的分解就是按照重要性顺序得到的 A A A 的 r r r 个秩一项,这一点非常重要。
【例1】什么时候 A = U Σ V T A=U\Sigma V^T A=UΣVT(奇异值)和 X Λ X − 1 X\Lambda X^{-1} XΛX−1 相同(特征值)?
解: A A A 的特征向量需要标准正交,才有 X = U = V X=U=V X=U=V,如果 A = Σ A=\Sigma A=Σ,也需要特征值 λ ≥ 0 \lambda\geq0 λ≥0,所以 A A A 必须是一个半正定(或正定)的对称矩阵。只有这样,才会有 A = X Λ X − 1 A=X\Lambda X^{-1} A=XΛX−1,就是 Q Λ Q T Q\Lambda Q^{T} QΛQT 和 A = U Σ V T A=U\Sigma V^{T} A=UΣVT 一致。
【例2】如果 A = x y T A=\boldsymbol x \boldsymbol y^T A=xyT(秩一),其中 x \boldsymbol x x 和 y \boldsymbol y y 都是单位向量,那么 A A A 的 SVD 是什么?
解: 式(7.2.2)中缩略版的 SVD 就是 x y T \boldsymbol x\boldsymbol y^T xyT,秩为 r = 1 r=1 r=1,其中 u 1 = x \boldsymbol u_1=\boldsymbol x u1=x, v 1 = y \boldsymbol v_1=\boldsymbol y v1=y 且 σ 1 = 1 \sigma_1=1 σ1=1。完全版的 SVD,要将 u 1 = x \boldsymbol u_1=\boldsymbol x u1=x 扩充为标准正交基 u i \boldsymbol u_i ui,然后将 v 1 = y \boldsymbol v_1=\boldsymbol y v1=y 扩充为标准正交基 v j \boldsymbol v_j vj,没有新的 σ \sigma σ,只有一个 σ 1 = 1 \sigma_1=1 σ1=1。
二、SVD 的证明
我们需要知道这令人惊叹的 u i \boldsymbol u_i ui 和 v j \boldsymbol v_j vj 是如何构造出来的。 v j \boldsymbol v_j vj 是 A T A \pmb{A^TA} ATA 的特征向量,这个一定是正确的,因为我们的目标是: A T A = ( U Σ V T ) T ( U Σ V T ) = V Σ T U T U Σ V T = V Σ T Σ V T ( 7.2.5 ) \pmb{A^TA}=(U\Sigma V^T)^T(U\Sigma V^T)=V\Sigma^TU^TU\Sigma V^T=\pmb{V\Sigma^T\Sigma V^T}\kern 20pt(7.2.5) ATA=(UΣVT)T(UΣVT)=VΣTUTUΣVT=VΣTΣVT(7.2.5)右侧包含了对称(半)正定矩阵 A T A A^TA ATA 的特征向量矩阵 V V V,并且 ( Σ T Σ ) (\Sigma^T\Sigma) (ΣTΣ) 是 ( A T A ) (A^TA) (ATA) 的特征值矩阵:每个 σ 2 \sigma^2 σ2 就是 ( A T A ) (A^TA) (ATA) 特征值 λ ( A T A ) \lambda(A^TA) λ(ATA)!
现在由 A v i = σ i u i A\boldsymbol v_i=\sigma_i\boldsymbol u_i Avi=σiui 可以得到单位向量 u 1 , u 2 , ⋯ , u r \boldsymbol u_1,\boldsymbol u_2,\cdots,\boldsymbol u_r u1,u2,⋯,ur,这就是关键的式(7.2.1),核心点,也就是 SVD 成功的全部原因,是这些单位向量 u 1 , u 2 , ⋯ , u r \boldsymbol u_1,\boldsymbol u_2,\cdots,\boldsymbol u_r u1,u2,⋯,ur 一定是两两正交(因为 v i \boldsymbol v_i vi 是正交的): 关键步骤 i ≠ j u i T u j = ( A v i σ i ) T ( A v j σ j ) = v i T A T A v j σ i σ j = σ j 2 σ i σ j v i T v j = 0 ( 7.2.6 ) \begin{array}{}\pmb{关键步骤}\\\pmb{i\neq j}\end{array}\kern 20pt\boldsymbol u_i^T\boldsymbol u_j=(\frac{A\boldsymbol v_i}{\sigma_i})^T(\frac{A\boldsymbol v_j}{\sigma_j})=\frac{\boldsymbol v_i^TA^TA\boldsymbol v_j}{\sigma_i\sigma_j}=\frac{\sigma_j^2}{\sigma_i\sigma_j}\boldsymbol v_i^T\boldsymbol v_j=0\kern 20pt(7.2.6) 关键步骤i=juiTuj=(σiAvi)T(σjAvj)=σiσjviTATAvj=σiσjσj2viTvj=0(7.2.6) v i \boldsymbol v_i vi 是 A T A A^TA ATA(对称)的特征向量,它们是正交的并且得到 u i \boldsymbol u_i ui 也是正交的。实际上 u i \boldsymbol u_i ui 是 A A T AA^T AAT 的特征向量。
最终,在 v j \boldsymbol v_j vj 和 u i \boldsymbol u_i ui 的基础上分别构造出了零空间 N ( A ) \pmb N(A) N(A) 和 左零空间 N ( A T ) \pmb N(A^T) N(AT) 的标准正交基,得到 n n n 个 v j \boldsymbol v_j vj 和 m m m 个 u i \boldsymbol u_i ui,得到 A = U Σ V T A=U\Sigma V^T A=UΣVT 中的 V , Σ V,\Sigma V,Σ 和 U U U。
三、SVD 的一个例子
下例演示了 A = U Σ V T A=U\Sigma V^T A=UΣVT 中全部三个矩阵的计算过程。
【例3】矩阵 A = [ 3 0 4 5 ] A=\begin{bmatrix}3&0\\4&5\end{bmatrix} A=[3405],秩为 r = 2 r=2 r=2,求出对应的矩阵 U , Σ , V U,\Sigma,V U,Σ,V。
解: 由于秩 r = 2 r=2 r=2,所以 A A A 有两个正的奇异值 σ 1 \sigma_1 σ1 和 σ 2 \sigma_2 σ2,下面会看到 σ 1 \sigma_1 σ1 比特征值 λ m a x = 5 \lambda_{max}=5 λmax=5 更大, σ 2 \sigma_2 σ2 比特征值 λ m i n = 3 \lambda_{min}=3 λmin=3 要更小,先从 A T A A^TA ATA 和 A A T AA^T AAT 开始: A T A = [ 25 20 20 25 ] A A T = [ 9 12 12 41 ] A^TA=\begin{bmatrix}25&20\\20&25\end{bmatrix}\kern 20ptAA^T=\begin{bmatrix}\kern 4pt9&12\\12&41\end{bmatrix} ATA=[25202025]AAT=[9121241]它们有相同的迹 ( 50 ) (50) (50) 和相同的特征值 σ 1 2 = 45 \sigma_1^2=45 σ12=45 和 σ 2 2 = 5 \sigma_2^2=5 σ22=5,取算术平方根得 σ 1 = 45 \sigma_1=\pmb{\sqrt{45}} σ1=45 和 σ 2 = 5 \sigma_2=\pmb{\sqrt5} σ2=5,则 σ 1 σ 2 = 15 \sigma_1\sigma_2=15 σ1σ2=15,也就是 A A A 的行列式。
关键步骤是求 A T A A^TA ATA 的特征向量(分别对应特征值 45 45 45 和 5 5 5): [ 25 20 20 25 ] [ 1 1 ] = 45 [ 1 1 ] [ 25 20 20 25 ] [ − 1 1 ] = 5 [ − 1 1 ] \begin{bmatrix}25&20\\20&25\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}=\pmb{45}\begin{bmatrix}1\\1\end{bmatrix}\kern 20pt\begin{bmatrix}25&20\\20&25\end{bmatrix}\begin{bmatrix}-1\\\kern 7pt1\end{bmatrix}=\pmb5\begin{bmatrix}-1\\\kern 7pt1\end{bmatrix} [25202025][11]=45[11][25202025][−11]=5[−11]然后将这些正交特征向量单位化,都除以 2 \sqrt2 2,即得到 v 1 \boldsymbol v_1 v1 和 v 2 \boldsymbol v_2 v2。 右奇异向量 v 1 = 1 2 [ 1 1 ] v 2 = 1 2 [ − 1 1 ] 左奇异向量 u i = A v i σ i \pmb{右奇异向量}\kern 10pt\boldsymbol v_1=\frac{1}{\sqrt2}\begin{bmatrix}1\\1\end{bmatrix}\kern 5pt\boldsymbol v_2=\frac{1}{\sqrt2}\begin{bmatrix}-1\\\kern 7pt1\end{bmatrix}\kern 10pt\pmb{左奇异向量}\kern 5pt\boldsymbol u_i=\frac{A\boldsymbol v_i}{\sigma_i} 右奇异向量v1=21[11]v2=21[−11]左奇异向量ui=σiAvi现在计算 A v 1 A\boldsymbol v_1 Av1 和 A v 2 A\boldsymbol v_2 Av2,它们分别是 σ 1 u 1 = 45 u 1 \sigma_1\boldsymbol u_1=\sqrt{45}\boldsymbol u_1 σ1u1=45u1 和 σ 2 u 2 = 5 u 2 \sigma_2\boldsymbol u_2=\sqrt5\boldsymbol u_2 σ2u2=5u2: A v 1 = 3 2 [ 1 3 ] = 45 1 10 [ 1 3 ] = σ 1 u 1 A v 2 = 1 2 [ − 3 1 ] = 5 1 10 [ − 3 1 ] = σ 2 u 2 \begin{array}{l}A\boldsymbol v_1=\displaystyle\frac{3}{\sqrt2}\begin{bmatrix}1\\3\end{bmatrix}=\sqrt{45}\pmb{\frac{1}{\sqrt{10}}\begin{bmatrix}1\\3\end{bmatrix}}=\sigma_1\boldsymbol u_1\\\\A\boldsymbol v_2=\displaystyle\frac{1}{\sqrt2}\begin{bmatrix}-3\\\kern 7pt1\end{bmatrix}=\sqrt5\pmb{\frac{1}{\sqrt{10}}\begin{bmatrix}-3\\\kern 7pt1\end{bmatrix}}=\sigma_2\boldsymbol u_2\end{array} Av1=23[13]=45101[13]=σ1u1Av2=21[−31]=5101[−31]=σ2u2除以 10 \sqrt{10} 10 使得 u 1 \boldsymbol u_1 u1 和 u 2 \boldsymbol u_2 u2 标准正交,然后可以得到预期的 σ 1 = 45 \sigma_1=\sqrt{45} σ1=45 和 σ 2 = 5 \sigma_2=\sqrt5 σ2=5。 A A A 的奇异值分解就是 U Σ V T U\Sigma V^T UΣVT。
U = 1 10 [ 1 − 3 3 1 ] Σ = [ 45 5 ] V = 1 2 [ 1 − 1 1 1 ] ( 7.2.7 ) \pmb U=\frac{1}{\sqrt{10}}\begin{bmatrix}1&-3\\3&\kern 7pt1\end{bmatrix}\kern 15pt\pmb\Sigma=\begin{bmatrix}\sqrt{45}\\&\sqrt5\end{bmatrix}\kern 15pt\pmb V=\frac{1}{\sqrt2}\begin{bmatrix}1&-1\\1&\kern 7pt1\end{bmatrix}\kern 20pt(7.2.7) U=101[13−31]Σ=[455]V=21[11−11](7.2.7)
U U U 和 V V V 包含列空间和行空间(两个空间都是 R 2 \pmb{\textrm R}^2 R2)的标准正交基。真正要做的是使用两组基对角化 A A A: A V = U Σ AV=U\Sigma AV=UΣ。矩阵 A A A 分解成了两个秩一矩阵(列乘行)的组合: σ 1 u 1 v 1 T + σ 2 u 2 v 2 T = 45 20 [ 1 1 3 3 ] + 5 20 [ 3 − 3 − 1 1 ] = [ 3 0 4 5 ] = A \sigma_1\boldsymbol u_1\boldsymbol v_1^T+\sigma_2\boldsymbol u_2\boldsymbol v_2^T=\pmb{\frac{\sqrt{45}}{\sqrt{20}}\begin{bmatrix}1&1\\3&3\end{bmatrix}+\frac{\sqrt5}{\sqrt{20}}\begin{bmatrix}\kern 7pt3&-3\\-1&\kern 7pt1\end{bmatrix}}=\begin{bmatrix}3&0\\4&5\end{bmatrix}=A σ1u1v1T+σ2u2v2T=2045[1313]+205[3−1−31]=[3405]=A
四、一个极端的矩阵
下面是一个阶数更大的矩阵的例子,它的 u i \boldsymbol u_i ui 和 v i \boldsymbol v_i vi 都是单位矩阵的列,所以计算很简单,但是要注意列的顺序。矩阵 A A A 非常的不平衡(它是一个严格的三角形矩阵),它所有的特征值都为零, A A T AA^T AAT 和 A T A A^TA ATA 并不接近,矩阵 U U U 和 V V V 是置换矩阵可以弥补这些问题。 A = [ 0 1 0 0 0 0 2 0 0 0 0 3 0 0 0 0 ] 特征值 λ = 0 , 0 , 0 , 0 全是零! 只有一个特征向量 ( 1 , 0 , 0 , 0 ) 奇异值 σ = 3 , 2 , 1 奇异向量是 I 的列 A=\begin{bmatrix}0&\pmb1&0&0\\0&0&\pmb2&0\\0&0&0&\pmb3\\0&0&0&0\end{bmatrix}\kern 20pt\begin{array}{l}特征值\,\lambda=0,0,0,0\,全是零!\\只有一个特征向量\,(1,0,0,0)\\奇异值\,\sigma=\pmb3,\pmb2,\pmb1\\奇异向量是\,I\,的列\end{array} A= 0000100002000030 特征值λ=0,0,0,0全是零!只有一个特征向量(1,0,0,0)奇异值σ=3,2,1奇异向量是I的列 A T A A^TA ATA 和 A A T AA^T AAT 都是对角矩阵(有简单的特征向量,但是顺序不同): A T A = [ 0 0 0 0 0 1 0 0 0 0 4 0 0 0 0 9 ] A A T = [ 1 0 0 0 0 4 0 0 0 0 9 0 0 0 0 0 ] A^TA=\begin{bmatrix}\pmb0&0&0&0\\0&\pmb1&0&0\\0&0&\pmb4&0\\0&0&0&\pmb9\end{bmatrix}\kern 20ptAA^T=\begin{bmatrix}\pmb1&0&0&0\\0&\pmb4&0&0\\0&0&\pmb9&0\\0&0&0&\pmb0\end{bmatrix} ATA= 0000010000400009 AAT= 1000040000900000 它们的特征向量( u i \boldsymbol u_i ui 对应 A A T AA^T AAT, v i \boldsymbol v_i vi 对应 A T A A^TA ATA)按照特征值减小的顺序 σ 1 2 > σ 2 2 > σ 3 2 \sigma_1^2>\sigma_2^2>\sigma_3^2 σ12>σ22>σ32 排列,这些特征值是 9 , 4 , 1 9,4,1 9,4,1。 U = [ 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 1 ] Σ = [ 3 2 1 0 ] V = [ 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 ] \pmb U=\begin{bmatrix}0&0&\pmb1&0\\0&\pmb1&0&0\\\pmb1&0&0&0\\0&0&0&\pmb1\end{bmatrix}\kern 15pt\Sigma=\begin{bmatrix}\pmb3\\&\pmb2\\&&\pmb1\\&&&0\end{bmatrix}\kern 15pt\pmb V=\begin{bmatrix}0&0&0&\pmb1\\0&0&\pmb1&0\\0&\pmb1&0&0\\\pmb1&0&0&0\end{bmatrix} U= 0010010010000001 Σ= 3210 V= 0001001001001000 U \pmb U U 和 V \pmb V V 的第一列 u 1 \boldsymbol u_1 u1 和 v 1 \boldsymbol v_1 v1 的分量 1 1 1 在第 3 3 3 位和第 4 4 4 位,则 u 1 σ 1 v 1 T \boldsymbol u_1\sigma_1\boldsymbol v_1^T u1σ1v1T 就表示矩阵 A A A 中最大的数 A 34 A_{34} A34,对于这个极端的例子,SVD 的三个秩一矩阵恰好来自于 A A A 中的数字 3 , 2 , 1 3,2,1 3,2,1。
A = U Σ V T = 3 u 1 v 1 T + 2 u 2 v 2 T + 1 u 3 v 3 T \pmb{A=U\Sigma V^T=3\boldsymbol u_1\boldsymbol v_1^T+2\boldsymbol u_2\boldsymbol v_2^T+1\boldsymbol u_3\boldsymbol v_3^T} A=UΣVT=3u1v1T+2u2v2T+1u3v3T
注:假设将 A A A 的最后一行(全零行)去掉,则 A A A 是一个 3 × 4 3\times4 3×4 的矩阵, A A T AA^T AAT 是 3 × 3 3\times3 3×3 的矩阵 —— 它的第四行和第四列都会消失, A T A A^TA ATA 和 A A T AA^T AAT 的特征值仍然是 λ = 1 , 4 , 9 \lambda=1,4,9 λ=1,4,9,也会在 Σ \Sigma Σ 中得到相同的奇异值 σ = 3 , 2 , 1 \sigma=3,2,1 σ=3,2,1。
A A A 的最后一行的全零行移除后,现在变成了 3 × 4 3\times4 3×4 的矩阵,也会移除 Σ \Sigma Σ 的最后一行和 U U U 的最后一列。则 ( 3 × 4 ) = U Σ V T = ( 3 × 3 ) ( 3 × 4 ) ( 4 × 4 ) (3\times4)=U\Sigma V^T=(3\times3)(3\times4)(4\times4) (3×4)=UΣVT=(3×3)(3×4)(4×4),SVD 完全适用于长方形矩阵。
一件好的事情是,由于矩阵 A A A 的行和列经常有完全不同的含义(如电子表格),如果要统计所有课程的成绩,那么可以用各列表示每个学生的情况,而各行表示每个课程的情况:则元素 a i j a_{ij} aij 就表示成绩。那么 σ 1 u 1 v 1 T \sigma_1\boldsymbol u_1\boldsymbol v_1^T σ1u1v1T 中, u 1 = \boldsymbol u_1= u1= 课程组合, v 1 = \boldsymbol v_1= v1= 学生组合,而 σ 1 \sigma_1 σ1 就是这些组合的成绩:最高成绩。
矩阵 A A A 也可以对一本杂志中关键词的出现频率计数: A A A 的列是不同的文章,每一行代表不同的词,那么 A A A 就是整个杂志的索引,其中最重要的信息就是 σ 1 u 1 v 1 T \sigma_1\boldsymbol u_1\boldsymbol v_1^T σ1u1v1T, σ 1 \sigma_1 σ1 就是高频词 u 1 \boldsymbol u_1 u1 在高频文章 v 1 \boldsymbol v_1 v1 出现的最高的频率。
五、奇异值的稳定性对比特征值的不稳定性
通过 4 × 4 4\times4 4×4 的矩阵 A A A 这个例子(一个极端情况)我们可以构造出一个特征值不稳定的例子。假设 ( 4 , 1 ) (4,1) (4,1) 元素从零变为 1 / 60000 1/60000 1/60000,这个几乎没有变化,秩变成了 4 4 4。 A = [ 0 1 0 0 0 0 2 0 0 0 0 3 1 60000 0 0 0 ] 仅仅是 1 / 60000 的微小改变, A 的特征值就发生了很大的变化: λ = 0 , 0 , 0 , 0 变为了 λ = 1 10 , i 10 , − 1 10 , − i 10 A=\begin{bmatrix}0&1&0&0\\0&0&2&0\\0&0&0&3\\\displaystyle\frac{1}{60000}&0&0&0\end{bmatrix}\kern 20pt\begin{array}{l}仅仅是\,1/60000\,的微小改变,A\\的特征值就发生了很大的变化:\\\lambda=0,0,0,0\,变为了\,\pmb{\lambda=\displaystyle\frac{1}{10},\frac{i}{10},\frac{-1}{10},\frac{-i}{10}}\end{array} A= 000600001100002000030 仅仅是1/60000的微小改变,A的特征值就发生了很大的变化:λ=0,0,0,0变为了λ=101,10i,10−1,10−i新元素仅仅变化了 1 / 60000 1/60000 1/60000,四个特征值就从零变化到了在复平面上以原点为圆心,半径为 1 10 \displaystyle\frac{1}{10} 101 的圆上,这表明当 A T A A^TA ATA 远离 A A T AA^T AAT 时特征值严重的不稳定性,在另外的极端情况下,如果 A T A = A A T A^TA=AA^T ATA=AAT(“正规矩阵”),那么 A A A 的特征向量正交且 A A A 的特征值完全稳定。
对比之下,任意矩阵的奇异值都是稳定的,它们不会超过 A A A 的变化。在这个例子中,新的奇异值是 3 , 2 , 1 \pmb{3,2,1} 3,2,1 和 1 / 60000 \pmb{1/60000} 1/60000,矩阵 U U U 和 V V V 保持不变, A A A 的 SVD 中的第四项是 σ 4 u 4 v 4 T \sigma_4\boldsymbol u_4\boldsymbol v_4^T σ4u4v4T,它有十五个零元素和一个小的元素 σ 4 = 1 / 60000 \sigma_4=1/60000 σ4=1/60000。
六、A 的奇异向量和 S = A T A S=A^TA S=ATA 的特征向量
式(7.2.5-7.2.6)同时证明了 SVD,奇异向量 v i \boldsymbol v_i vi 是 S = A T A S=A^TA S=ATA 的特征向量 q i \boldsymbol q_i qi。 S S S 的特征值 λ i \lambda_i λi 和 A A A 相应的奇异值的平方 σ i 2 \sigma_i^2 σi2 相等, S S S 的秩 r r r 等于 A A A 的秩。特征向量和奇异向量的展开式是完美对应的。
对称矩阵 S S = Q Λ Q T = λ 1 q 1 q 1 T + λ 2 q 2 q 2 T + ⋯ + λ r q r q r T 任意矩阵 A A = U Σ V T = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ r u r v r T \begin{array}{l}\pmb{对称矩阵\,S}\kern 25pt\color{blue}S=Q\Lambda Q^T=\lambda_1\boldsymbol q_1\boldsymbol q_1^T+\lambda_2\boldsymbol q_2\boldsymbol q_2^T+\cdots+\lambda_r\boldsymbol q_r\boldsymbol q_r^T\\\pmb{任意矩阵\,A}\kern 23pt\color{blue}A=U\Sigma V^T=\sigma_1\boldsymbol u_1\boldsymbol v_1^T+\sigma_2\boldsymbol u_2\boldsymbol v_2^T+\cdots+\sigma_r\boldsymbol u_r\boldsymbol v_r^T\end{array} 对称矩阵SS=QΛQT=λ1q1q1T+λ2q2q2T+⋯+λrqrqrT任意矩阵AA=UΣVT=σ1u1v1T+σ2u2v2T+⋯+σrurvrT
各个 q i \boldsymbol q_i qi 是正交的,各个 u i \boldsymbol u_i ui 是正交的,各个 v i \boldsymbol v_i vi 也是正交的,非常漂亮!
但是还要更深入理解,有以下两个原因:其一是要弥补特征值部分的短板, 如果 λ \lambda λ 是 S S S 的二重特征值,我们能够且一定可以找出两个标准正交的向量。另一个原因是要明白 SVD 是如何选出在 σ 2 u 2 v 2 T \sigma_2\boldsymbol u_2\boldsymbol v_2^T σ2u2v2T 之前的最大项 σ 1 u 1 v 1 T \sigma_1\boldsymbol u_1\boldsymbol v_1^T σ1u1v1T。需要理解的是 S S S 的特征值 λ \lambda λ 和 A A A 的奇异值 σ \sigma σ,而不只是求出它们。
从 S S S 最大的特征值 λ 1 \lambda_1 λ1 开始,它解决了下面的这个问题:
λ 1 = max x T S x x T x \pmb{\lambda_1=\textrm{max}\,\displaystyle\frac{\boldsymbol x^TS\boldsymbol x}{\boldsymbol x^T\boldsymbol x}} λ1=maxxTxxTSx,这个向量是 x = q 1 \boldsymbol x=\boldsymbol q_1 x=q1,且 S q 1 = λ 1 q 1 S\boldsymbol q_1=\lambda_1\boldsymbol q_1\kern 20pt Sq1=λ1q1(7.2.8)
\,
对比 A A A 最大的奇异值 σ 1 \sigma_1 σ1,它解决的这个问题是:
σ 1 = max ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ \pmb{\sigma_1=\max\displaystyle\frac{||A\boldsymbol x||}{||\boldsymbol x||}} σ1=max∣∣x∣∣∣∣Ax∣∣,这个向量是 x = v 1 \boldsymbol x=\boldsymbol v_1 x=v1 且 A v 1 = σ 1 u 1 A\boldsymbol v_1=\sigma_1\boldsymbol u_1\kern 20pt Av1=σ1u1(7.2.9)
从式(7.2.8)可以推出(7.2.9),由于 S = A T A S=A^TA S=ATA,所以 x T S x x T x = x T A T A x x T x = ( A x ) T ( A x ) x T x = ∣ ∣ A x ∣ ∣ 2 ∣ ∣ x ∣ ∣ 2 = σ 2 \displaystyle\frac{\boldsymbol x^TS\boldsymbol x}{\boldsymbol x^T\boldsymbol x}=\frac{\boldsymbol x^TA^TA\boldsymbol x}{\boldsymbol x^T\boldsymbol x}=\frac{(A\boldsymbol x)^T(A\boldsymbol x)}{\boldsymbol x^T\boldsymbol x}=\frac{||A\boldsymbol x||^2}{||\boldsymbol x||^2}=\sigma^2 xTxxTSx=xTxxTATAx=xTx(Ax)T(Ax)=∣∣x∣∣2∣∣Ax∣∣2=σ2。
这个一次找到一个值的方法也可以适用于 λ 2 \lambda_2 λ2 和 σ 2 \sigma_2 σ2,但是并不是任意的 x \boldsymbol x x 都可以:
λ 2 = max x T S x x T x \pmb{\lambda_2=\max\displaystyle\frac{\boldsymbol x^TS\boldsymbol x}{\boldsymbol x^T\boldsymbol x}} λ2=maxxTxxTSx,其中 x \boldsymbol x x 满足 q 1 T x = 0 \boldsymbol q_1^T\boldsymbol x=0 q1Tx=0,最大的是 x = q 2 \boldsymbol x=\boldsymbol q_2\kern 20pt x=q2(7.2.10)
\,
σ 2 = max ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ \pmb{\sigma_2=\max\displaystyle\frac{||A\boldsymbol x||}{||\boldsymbol x||}} σ2=max∣∣x∣∣∣∣Ax∣∣,其中 x \boldsymbol x x 满足 v 1 T x = 0 \boldsymbol v_1^T\boldsymbol x=0 v1Tx=0,最大的是 x = v 2 \boldsymbol x=\boldsymbol v_2\kern 20pt x=v2(7.2.11)
当 S = A T A S=A^TA S=ATA 时,可以得到 λ 1 = σ 1 2 \lambda_1=\sigma_1^2 λ1=σ12 和 λ 2 = σ 2 2 \lambda_2=\sigma_2^2 λ2=σ22,为什么这个方法会成功呢?
从比值 r ( x ) = x T S x x T x r(\boldsymbol x)=\displaystyle\frac{\boldsymbol x^TS\boldsymbol x}{\boldsymbol x^T\boldsymbol x} r(x)=xTxxTSx 开始,这个称为瑞利商(Rayleigh quotient),要求 r ( x ) r(\boldsymbol x) r(x) 的最大值,要令其偏导数为零: ∂ r ∂ x i = 0 , i = 1 , 2 , ⋯ , n \displaystyle\frac{\partial r}{\partial x_i}=0,i=1,2,\cdots,n ∂xi∂r=0,i=1,2,⋯,n。这些导数的求解比较困难,下面是结果:瑞利商最大时的向量 x \boldsymbol x x: 当 S x = r ( x ) x 时, r ( x ) = x T S x x T x 的偏导数全为零 ( 7.2.12 ) 当\,S\boldsymbol x=r(\boldsymbol x)\boldsymbol x\,时,\pmb{r(\boldsymbol x)=\frac{\boldsymbol x^TS\boldsymbol x}{\boldsymbol x^T\boldsymbol x}\,的偏导数全为零}\kern 20pt(7.2.12) 当Sx=r(x)x时,r(x)=xTxxTSx的偏导数全为零(7.2.12)所以向量 x \boldsymbol x x 是 S S S 的特征向量,最大的比值 r ( x ) r(\boldsymbol x) r(x) 就是 S S S 最大的特征值 λ 1 \lambda_1 λ1。下面转而讨论 A A A —— 注意它和 S = A T A S=A^TA S=ATA 的联系! 最大化 ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ ,也会最大化 ( ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ ) 2 = x T A T A x x T x = x T S x x x 最大化\,\frac{||A\boldsymbol x||}{||\boldsymbol x||},也会最大化\,\Big(\frac{||A\boldsymbol x||}{||\boldsymbol x||}\Big)^2=\frac{\boldsymbol x^TA^TA\boldsymbol x}{\boldsymbol x^T\boldsymbol x}=\frac{\boldsymbol x^TS\boldsymbol x}{\boldsymbol x\boldsymbol x} 最大化∣∣x∣∣∣∣Ax∣∣,也会最大化(∣∣x∣∣∣∣Ax∣∣)2=xTxxTATAx=xxxTSx所以式(7.2.9)中 x = v 1 \boldsymbol x=\boldsymbol v_1 x=v1 与式(7.2.8)中 S = A T A S=A^TA S=ATA 最前面的特征向量 q 1 \boldsymbol q_1 q1 相同。
下面解释为什么式(7.2.10)和(7.2.11)中的向量为什么是 q 2 \boldsymbol q_2 q2 和 v 2 \boldsymbol v_2 v2。它们分别与 q 1 \boldsymbol q_1 q1 和 v 1 \boldsymbol v_1 v1 正交,因此是在考虑范围内。
任意的正交向量 Q 1 Q_1 Q1 的首列是 q 1 \boldsymbol q_1 q1,剩余的 n − 1 n-1 n−1 个标准正交列都与 q 1 \boldsymbol q_1 q1 正交,使用 S q 1 = λ 1 q 1 S\boldsymbol q_1=\lambda_1\boldsymbol q_1 Sq1=λ1q1: S Q 1 = S [ q 1 q 2 ⋯ q n ] = [ q 1 q 2 ⋯ q n ] [ λ 1 w T 0 S n − 1 ] = Q 1 [ λ 1 w T 0 S n − 1 ] ( 7.2.13 ) SQ_1=S\begin{bmatrix}\boldsymbol q_1&\boldsymbol q_2&\cdots&\boldsymbol q_n\end{bmatrix}=\begin{bmatrix}\boldsymbol q_1&\boldsymbol q_2&\cdots&\boldsymbol q_n\end{bmatrix}\begin{bmatrix}\lambda_1&\boldsymbol w^T\\\boldsymbol 0&S_{n-1}\end{bmatrix}=Q_1\begin{bmatrix}\lambda_1&\boldsymbol w^T\\\boldsymbol 0&S_{n-1}\end{bmatrix}\kern 15pt(7.2.13) SQ1=S[q1q2⋯qn]=[q1q2⋯qn][λ10wTSn−1]=Q1[λ10wTSn−1](7.2.13)其中 w T \boldsymbol w^T wT 表示的是 S S S 作用于 q 1 \boldsymbol q_1 q1, S n − 1 S_{n-1} Sn−1 是降维后的矩阵,利用矩阵的乘法,将它们乘开,第一列即 λ 1 q 1 \lambda_1\boldsymbol q_1 λ1q1,后面的即为 w T q 1 + S n − 1 [ q 2 ⋯ q n ] \boldsymbol w^T\boldsymbol q_1+S_{n-1}\begin{bmatrix}\boldsymbol q_2&\cdots&\boldsymbol q_n\end{bmatrix} wTq1+Sn−1[q2⋯qn]。再用 Q 1 T Q_1^T Q1T 左乘上式,注意到 Q 1 T Q 1 = I Q_1^TQ_1=I Q1TQ1=I,且 Q 1 T S Q 1 Q_1^TSQ_1 Q1TSQ1 是像 S S S 一样的对称矩阵: 对称矩阵 Q 1 T S Q 1 = [ λ 1 w T 0 S n − 1 ] 将强制 w = 0 且 S n − 1 T = S n − 1 对称矩阵\,Q_1^TSQ_1=\begin{bmatrix}\lambda_1&\boldsymbol w^T\\\boldsymbol 0&S_{n-1}\end{bmatrix}将强制\,\boldsymbol w=\boldsymbol 0\,且\,S^T_{n-1}=S_{n-1} 对称矩阵Q1TSQ1=[λ10wTSn−1]将强制w=0且Sn−1T=Sn−1根据条件 q 1 T x = 0 \boldsymbol q_1^T\boldsymbol x=0 q1Tx=0 将问题(7.2.10)的最大值问题简化成了 n − 1 n-1 n−1 阶的情况, S n − 1 S_{n-1} Sn−1 最大的特征值将是 S S S 的第二大特征值,就是 λ 2 \lambda_2 λ2,式(7.2.10)中的向量是特征向量 q 2 \boldsymbol q_2 q2 且 S q 2 = λ 2 q 2 S\boldsymbol q_2=\lambda_2\boldsymbol q_2 Sq2=λ2q2。
继续下去,或者使用数学归纳法,就可以得到所有的特征向量 q 1 , q 2 , ⋯ , q 2 \boldsymbol q_1,\boldsymbol q_2,\cdots,\boldsymbol q_2 q1,q2,⋯,q2 和它们对应的特征值 λ 1 , λ 2 , ⋯ λ n \lambda_1,\lambda_2,\cdots\,\lambda_n λ1,λ2,⋯λn,即使存在重复的特征值,谱定理 S = Q Λ Q T S=Q\Lambda Q^T S=QΛQT 也可以被证明。所有的对称矩阵都可被对角化。
类似的,SVD 可以从式(7.2.9)和(7.2.11)中一步一步的得到。下面有一个很重要的问题:实际情况中如何计算 λ \lambda λ 和 σ \sigma σ 呢?
七、计算 S 的特征值和 A 的奇异值
A A A 的奇异值 σ i \sigma_i σi 是 S = A T A S=A^TA S=ATA 特征值 λ i \lambda_i λi 的算术平方根,这个将 SVD 和对称矩阵的特征值问题联系了起来,这个很好;但是我们不想使用 A T A A^TA ATA 乘 A A A,因为这个运算非常耗时,这个很不好。
首先想到的是尽可能将 A A A 和 S S S 的元素都变成零,而不改变任何的 σ \sigma σ 和 λ \lambda λ。奇异向量和特征向量会改变 —— 这个没有问题。相似矩阵 Q − 1 S Q Q^{-1}SQ Q−1SQ 和 S S S 的特征值 λ \lambda λ 相同,如果 S S S 正交,那么这个矩阵就是 Q T S Q Q^TSQ QTSQ 也是对称的。
对于二阶的对称矩阵可以构造出 2 × 2 2\times2 2×2 的旋转矩阵 Q Q Q,使得 Q T S Q Q^TSQ QTSQ 是对称的三对角矩阵(symmetric and tridiagonal matrix),它含有大量的零元素,但是旋转无法保证总能得到对角矩阵,所以要想求得 S S S 所有的特征值,需要新的方法。
对于 SVD,和 Q T S Q Q^TSQ QTSQ 相对应的是什么?我们不想改变 A A A 任何的奇异值,那么就是:在 A A A 的两边分别乘上不同的正交矩阵 Q 1 Q_1 Q1 和 Q 2 Q_2 Q2,利用这两个在矩阵 Q 1 T A Q 2 Q_1^TAQ_2 Q1TAQ2 中生成零元素,而 σ \sigma σ 不会改变: ( Q 1 T A Q 2 ) T ( Q 1 T A Q 2 ) = Q 2 T A T A Q 2 = Q 2 T S Q 2 得到相同的 σ ( A ) 和 λ ( S ) (Q_1^TAQ_2)^T(Q_1^TAQ_2)=Q_2^TA^TAQ_2=Q_2^TSQ_2\kern 10pt得到相同的\,\sigma(A)\,和\,\lambda(S) (Q1TAQ2)T(Q1TAQ2)=Q2TATAQ2=Q2TSQ2得到相同的σ(A)和λ(S)两个自由选取的 Q Q Q 将可以使得 Q 1 T A Q 2 Q_1^TAQ_2 Q1TAQ2 为两对角矩阵(bidiagonal matrix),这个完美对应了 Q T S Q Q^TSQ QTSQ 是三对角矩阵,它们之间的联系是: ( 两对角矩阵 ) T ( 两对角矩阵 ) = 三对角矩阵 (两对角矩阵)^T(两对角矩阵)=三对角矩阵 (两对角矩阵)T(两对角矩阵)=三对角矩阵。
最后要算出对角矩阵 Λ \Lambda Λ 和对角矩阵 Σ \Sigma Σ 的步骤需要更多的新思路,这个也不简单,因为有些要解的 det ( S − λ I ) = 0 \det(S-\lambda I)=0 det(S−λI)=0 是 n = 100 n=100 n=100 或 1000 1000 1000 甚至是更多次数的多项式,而我们不可能去求解这些多项式!
LAPACK 中求解 λ \lambda λ 和 σ \sigma σ 是使用简单的正交矩阵来逼近 Q T S Q = Λ Q^TSQ=\Lambda QTSQ=Λ 和 U T A V = Σ U^TAV=\Sigma UTAV=Σ,当很接近 Λ \Lambda Λ 和 Σ \Sigma Σ 时就停止。
这两步(先是零元素)方法在指令 eig(S) 和 svd(A) 中内置了。
八、主要内容总结
- SVD 将 A A A 分解成 U Σ V T U\Sigma V^T UΣVT,共有 r r r 个奇异值 σ 1 ≥ σ 2 ≥ ⋯ ≥ σ r > 0 \sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r>0 σ1≥σ2≥⋯≥σr>0.
- 数值 σ 1 2 , σ 2 2 , ⋯ , σ r 2 \sigma_1^2,\sigma_2^2,\cdots,\sigma_r^2 σ12,σ22,⋯,σr2 是 A A T AA^T AAT 和 A T A A^TA ATA 非零的特征值。
- U U U 和 V V V 的标准正交列是 A A T AA^T AAT 和 A T A A^TA ATA 的特征向量。
- 这些列包含了矩阵 A A A 四个基本子空间的标准正交基。
- 这些基对角化矩阵 A A A: A v i = σ i u i , i ≤ r A\boldsymbol v_i=\sigma_i\boldsymbol u_i,\,i\leq r Avi=σiui,i≤r,即是 A V = U Σ \pmb{AV=U\Sigma} AV=UΣ.
- A = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ r u r v r T A=\sigma_1\boldsymbol u_1\boldsymbol v_1^T+\sigma_2\boldsymbol u_2\boldsymbol v_2^T+\cdots+\sigma_r\boldsymbol u_r\boldsymbol v_r^T A=σ1u1v1T+σ2u2v2T+⋯+σrurvrT,其中 σ 1 \sigma_1 σ1 是比值 ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ \displaystyle\frac{||A\boldsymbol x||}{||\boldsymbol x||} ∣∣x∣∣∣∣Ax∣∣ 的最大值。
九、例题
【例4】识别出下列将 A A A 分解成列乘行的和的分解方式的类型: 1. 正交列 u 1 σ 1 , u 2 σ 2 , ⋯ , u r σ r 乘 标准正交行 v 1 T , v 2 T , ⋯ , v r T 2. 标准正交列 q 1 , q 2 , ⋯ , q r 乘 三角形矩阵的行 r 1 T , r 2 T , ⋯ , r r T 3. 三角形矩阵的列 l 1 , l 2 , ⋯ , l r 乘 三角形矩阵的行 u 1 T , u 2 T ⋯ , u r T \begin{array}{llll}1.\,正交列&\boldsymbol u_1\sigma_1,\boldsymbol u_2\sigma_2,\cdots,\boldsymbol u_r\sigma_r&乘&标准正交行&\boldsymbol v_1^T,\boldsymbol v_2^T,\cdots,\boldsymbol v_r^T\\2.\,标准正交列&\boldsymbol q_1,\boldsymbol q_2,\cdots,\boldsymbol q_r&乘&三角形矩阵的行&\boldsymbol r_1^T,\boldsymbol r_2^T,\cdots,\boldsymbol r_r^T\\3.\,三角形矩阵的列&\boldsymbol l_1,\boldsymbol l_2,\cdots,\boldsymbol l_r&乘&三角形矩阵的行&\boldsymbol u_1^T,\boldsymbol u_2^T\cdots,\boldsymbol u_r^T\end{array} 1.正交列2.标准正交列3.三角形矩阵的列u1σ1,u2σ2,⋯,urσrq1,q2,⋯,qrl1,l2,⋯,lr乘乘乘标准正交行三角形矩阵的行三角形矩阵的行v1T,v2T,⋯,vrTr1T,r2T,⋯,rrTu1T,u2T⋯,urT A A A 的秩、主元和奇异值在上述分解中的哪里出现?
解: 这三种分解不管是对理论数学还是应用数学中的线性代数都是基础:
- 奇异值分解 Singular Value Decompositon: A = U Σ V T \pmb{A=U\Sigma V^T} A=UΣVT
- 格拉姆-施密特正交化 Gram-Schmidt Orthogonalization: A = Q R \pmb{A=QR} A=QR
- 高斯消元法 Gaussian Elimination: A = L U \pmb{A=LU} A=LU
可以将奇异值 σ i \pmb{\sigma_i} σi、高度 h i \pmb{h_i} hi 和主元 d i \pmb{d_i} di 单独表示:
- A = U Σ V T A=U\Sigma V^T A=UΣVT,其中 U U U 和 V V V 的列都是单位向量, r r r 个奇异值 σ i \sigma_i σi 在 Σ \Sigma Σ 中.
- A = Q H R A=QHR A=QHR,其中 Q Q Q 的列是单位向量, R R R 中的对角元素都是 1 1 1, r r r 个高度 h i h_i hi 在 H H H 中.
- A = L D U A=LDU A=LDU,其中 L L L 和 U U U 的对角元素都是 1 1 1, r r r 个主元在 D D D 中.
每个 h i h_i hi 表示第 i i i 列到由第 1 , 2 , ⋯ , i − 1 1,2,\cdots,i-1 1,2,⋯,i−1 列所形成平面的高度,当 r = m = n r=m=n r=m=n 时, n n n 维的 “平行多面体”(以 A A A 各列为同一顶点处的棱)的体积可以由 A = U Σ V T = L D U = Q H R A=U\Sigma V^T=LDU=QHR A=UΣVT=LDU=QHR 求得: ∣ det A ∣ = ∣ σ i 的乘积 ∣ = ∣ d i 的乘积 ∣ = ∣ h i 的乘积 ∣ \pmb{|\det A|=|\sigma_i 的乘积|=|d_i\,的乘积|=|h_i\,的乘积|} ∣detA∣=∣σi的乘积∣=∣di的乘积∣=∣hi的乘积∣【例5】证明 σ 1 ≥ ∣ λ ∣ max \pmb{\sigma_1\ge|\lambda|_{\textrm{max}}} σ1≥∣λ∣max,最大的奇异值大于或等于所有的特征值。
证明: 由 A = U Σ V T A=U\Sigma V^T A=UΣVT,注意到左乘一个正交矩阵并不改变这个向量的长度: ∣ ∣ Q x ∣ ∣ = ∣ ∣ x ∣ ∣ ||Q\boldsymbol x||=||\boldsymbol x|| ∣∣Qx∣∣=∣∣x∣∣,这是因为 ∣ ∣ Q x ∣ ∣ 2 = x T Q T Q x = x T x = ∣ ∣ x ∣ ∣ 2 ||Q\boldsymbol x||^2=\boldsymbol x^TQ^TQ\boldsymbol x=\boldsymbol x^T\boldsymbol x=||\boldsymbol x||^2 ∣∣Qx∣∣2=xTQTQx=xTx=∣∣x∣∣2,这个也适用于 Q = U Q=U Q=U 和 Q = V T Q=V^T Q=VT,这两个矩阵的中间是对角矩阵 Σ \Sigma Σ: ∣ ∣ A x ∣ ∣ = ∣ ∣ U Σ V T x ∣ ∣ = ∣ ∣ Σ V T x ∣ ∣ ≤ σ 1 ∣ ∣ V T x ∣ ∣ = σ 1 ∣ ∣ x ∣ ∣ ( 7.2.14 ) ||A\boldsymbol x||=||U\Sigma V^T\boldsymbol x||=||\Sigma V^T\boldsymbol x||\le\sigma_1||V^T\boldsymbol x||=\sigma_1||\boldsymbol x||\kern 20pt(7.2.14) ∣∣Ax∣∣=∣∣UΣVTx∣∣=∣∣ΣVTx∣∣≤σ1∣∣VTx∣∣=σ1∣∣x∣∣(7.2.14)特征向量满足 ∣ ∣ A x ∣ ∣ = ∣ λ ∣ ∣ ∣ x ∣ ∣ ||A\boldsymbol x||=|\lambda|||\boldsymbol x|| ∣∣Ax∣∣=∣λ∣∣∣x∣∣,所以式(7.2.14)表明 ∣ λ ∣ ∣ ∣ x ∣ ∣ ≤ σ 1 ∣ ∣ x ∣ ∣ |\lambda|||\boldsymbol x||\le\sigma_1||\boldsymbol x|| ∣λ∣∣∣x∣∣≤σ1∣∣x∣∣,所以 ∣ λ ∣ ≤ σ 1 \pmb{|\lambda|\le\sigma_1} ∣λ∣≤σ1.
取 x = ( 1 , 0 , ⋯ , 0 ) \boldsymbol x=(1,0,\cdots,0) x=(1,0,⋯,0) 为单位向量,则 A x A\boldsymbol x Ax 就是 A A A 的第一列,然后由不等式(7.2.14)可得,这列的长度小于或等于 σ 1 \sigma_1 σ1。所以 A A A 的每个元素都有 ∣ a i j ∣ ≤ σ 1 |a_{ij}|\le\sigma_1 ∣aij∣≤σ1.
式(7.2.14)再次证明了 ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ \displaystyle\frac{||A\boldsymbol x||}{||\boldsymbol x||} ∣∣x∣∣∣∣Ax∣∣ 的最大值等于 σ 1 \sigma_1 σ1.
在求解 A x = b A\boldsymbol x=\boldsymbol b Ax=b 时,条件数(condition number) σ max σ min \displaystyle\frac{\sigma_{\textrm{max}}}{\sigma_{\textrm{min}}} σminσmax 控制舍入的误差,如果条件数太大,那么 MATLAB 会警告此时的 x \boldsymbol x x 不可靠。
相关文章:

7.2 奇异值分解的基与矩阵
一、奇异值分解 奇异值分解(SVD)是线性代数的高光时刻。 A A A 是一个 m n m\times n mn 的矩阵,可以是方阵或者长方形矩阵,秩为 r r r。我们要对角化 A A A,但并不是把它化成 X − 1 A X X^{-1}A X X−1AX 的形…...

PDFMathTranslate安装使用
PDF全文翻译!!!! PDFMathTranslate安装使用 它是个啥 PDFMathTranslate 可能是一个用于 PDF 文件的数学公式翻译 工具。它可能包含以下功能: 提取 PDF 内的数学公式 将数学公式转换成 LaTeX 代码 翻译数学公式的内…...

STL之list的使用(超详解)
目录 一、list的介绍及使用 1.1 list的介绍 1.2 list的使用 1.2.1 list的构造 1.2.2 iterator的使用 1.2.3capacity(容量相关) 1.2.4 element access(元素访问) 1.2.5 modifiers(链表修改)…...

动态 SQL 的使用
目录 1、< if> 标签2、< trim> 标签3、< where> 标签4、< set> 标签5、< foreach> 标签 1、< if> 标签 < if test“条件语句”> xxxx < /if> 只有当条件语句满足条件,才会拼接 < if> 标签内容,因…...

【如何删除在 Linux 系统中的删除乱码文件】
如何删除在 Linux 系统中的删除乱码文件 1. 列出文件并找到乱码文件:2. 使用通配符(谨慎使用):3. 转义特殊字符:4. 使用 find 命令:5. 使用 inode 号删除文件:6. 图形界面文件管理器:…...

防火墙IPSec (无固定IP地址---一对多)
目录 前言 一、场景: 二、实现 1.拓扑图 2.配置思路 ①基础通信配置 ②PPPoE配置 ③总部的模版IPSec配置 ④分部的IPSec配置 ⑤NAT配置 3.具体配置 ①基础配置 ②详细配置和顺序 效果测试: ③PPPOE ①配置PPPoE ②策略放行 ③IPSec与NA…...

基于SpringBoot的智能问诊系统设计与隐私保护策略
通过SpringBoot框架,我们可以快速搭建一个智能问诊系统,为用户提供便捷的线上医疗服务。然而,在系统设计和实现过程中,如何保障用户的隐私和数据安全,始终是一个亟需关注的问题。本文将探讨基于SpringBoot的智能问诊系…...

DeepSeek进阶应用(一):结合Mermaid绘图(流程图、时序图、类图、状态图、甘特图、饼图)
🌟前言: 在软件开发、项目管理和系统设计等领域,图表是表达复杂信息的有效工具。随着AI助手如DeepSeek的普及,我们现在可以更轻松地创建各种专业图表。 名人说:博观而约取,厚积而薄发。——苏轼《稼说送张琥》 创作者&…...

Ubuntu 下 nginx-1.24.0 源码分析 - ngx_init_cycle 函数
nei声明在 src/core/ngx_cycle.h ngx_cycle_t *ngx_init_cycle(ngx_cycle_t *old_cycle);实现在 src/core/ngx_cycle.c ngx_cycle_t * ngx_init_cycle(ngx_cycle_t *old_cycle) {void *rv;char **senv;ngx_uint_t i, n;ngx_log_t …...

【redis】数据类型之geo
Redis的GEO数据类型用于存储地理位置信息(如经纬度),并提供高效的地理位置查询功能(如计算两地距离、搜索附近地点等)。其底层基于Sorted Set(有序集合)实现,通过Geohash编码将经纬度…...
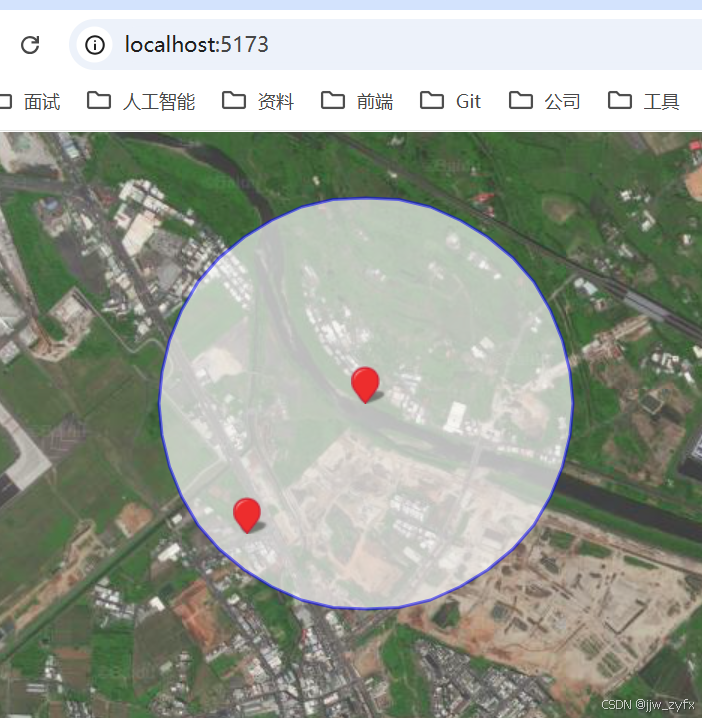
vue3 vite或者vue2 百度地图(卫星图)离线使用详细讲解
1、在Windows上下载瓦片,使用的工具为: 全能电子地图下载器3.0最新版(推荐) 下载后解压,然后进入目录"全能电子地图下载器3.0最新版(推荐)\全能电子地图下载器3.0\MapTileDownloader" 在这个目录…...

《Python实战进阶》No17: 数据库连接与 ORM(SQLAlchemy 实战)
No17: 数据库连接与 ORM(SQLAlchemy 实战) 摘要 本文深入探讨SQLAlchemy在复杂场景下的高级应用,涵盖四大核心主题: 会话生命周期管理:通过事件钩子实现事务监控与审计追踪混合继承映射:结合单表/连接表继…...
--前端音视频处理)
工程化与框架系列(27)--前端音视频处理
前端音视频处理 🎥 引言 前端音视频处理是现代Web应用中的重要组成部分,涉及音频播放、视频处理、流媒体传输等多个方面。本文将深入探讨前端音视频处理的关键技术和最佳实践,帮助开发者构建高质量的多媒体应用。 音视频技术概述 前端音视…...
芋道打包时报错:缺失@unocss插件
在遇到打包时,报这个错误,提示构建失败是因为 ESLint 在加载 unocss 插件时,找不到 unocss/eslint-plugin 模块 解决办法:安装缺失的依赖:保证unocss/eslint-plugin已经被正确安装, 使用以下命令安装&…...
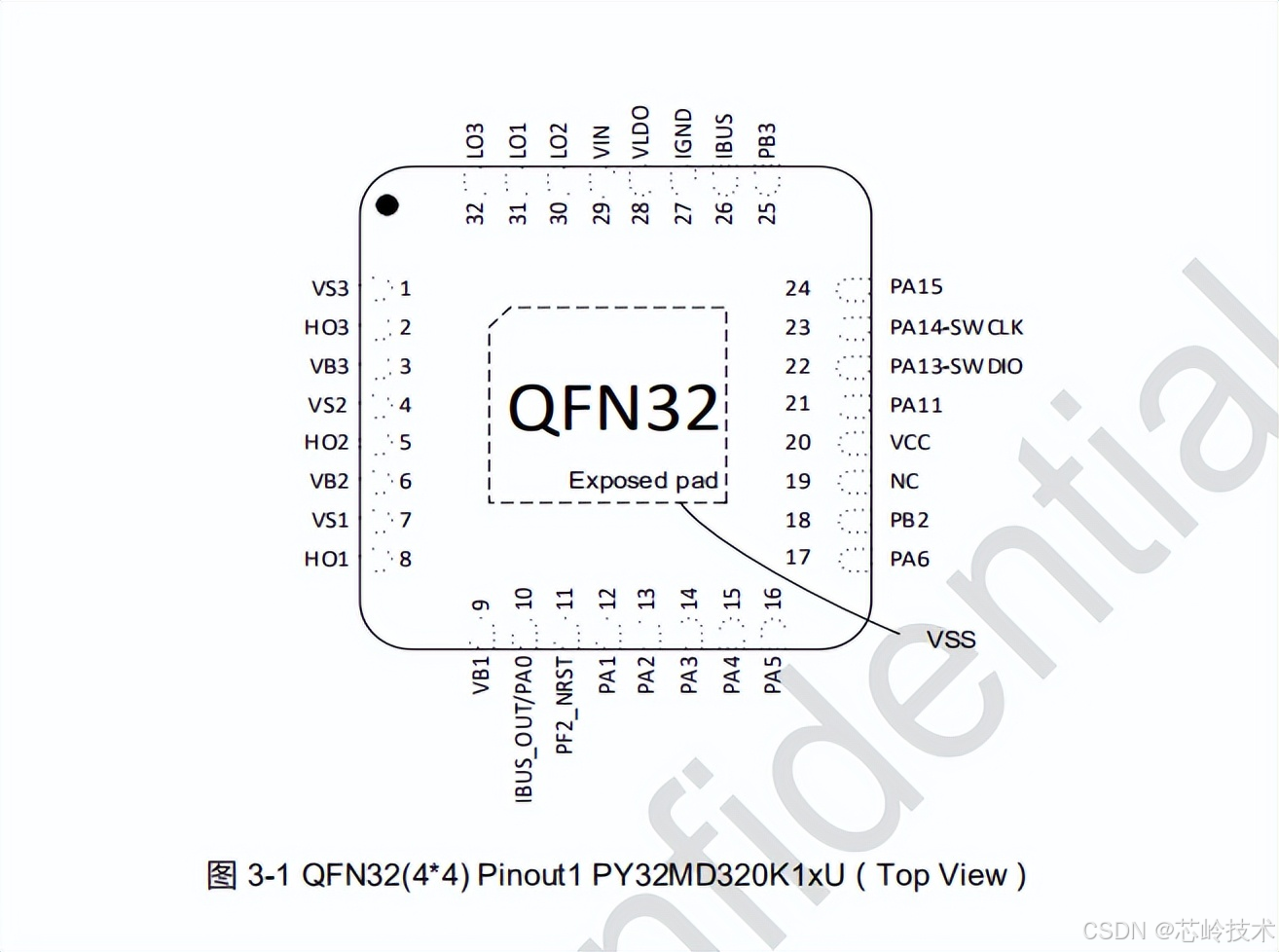
PY32MD320单片机 QFN32封装,内置多功能三相 NN 型预驱。
PY32MD320单片机是普冉半导体的一款电机专用MCU,芯片采用了高性能的 32 位 ARM Cortex-M0 内核,主要用于电机控制。PY32MD320嵌入高达 64 KB Flash 和 8 KB SRAM 存储器,最高工作频率 48 MHz。PY32MD320单片机的工作温度范围为 -40 ~ 105 ℃&…...

深入解析 configService.addListener 使用中的注意事项
在使用 Nacos 的 configService.addListener 方法进行配置监听时,为了确保程序的稳定性、可靠性以及高效性,有诸多注意事项需要我们关注。下面将对这些关键要点进行详细阐述。 一、连接稳定性 1.1 网络连接问题 Nacos 客户端与服务端通过网络进行通信&…...
)
Windows控制台函数:控制台读取输入函数ReadConsoleA()
目录 什么是 ReadConsoleA? 它长什么样? 怎么用它? 它跟 std::cin 有什么不一样? 注意事项 什么是 ReadConsoleA? ReadConsoleA 是一个 Windows API 函数,用来从控制台读取用户输入。想象一下&#…...
)
奇安信 2025 年护网蓝队初选笔试题(附答案解析)
🔥 爆款 CSDN 题库 | 超全护网蓝队笔试真题 | 含详细答案解析 🔥 熬夜为大家整理了 奇安信 2025 年护网蓝队初选笔试题,(关注我我会持续更新)涵盖 SQL 注入、Web 安全、渗透测试、二进制安全 等核心知识点,…...
国产编辑器EverEdit - Web预览设置
1 设置-高级-Web预览 1.1 设置说明 选择主菜单工具 -> 设置 -> 常规,在弹出的选项窗口中选择Web预览分类,如下图所示: 1.1.1 本地浏览HTML文件 如果用户只是在本地浏览HTML文件,即直接用浏览器打开HTML文件,确…...

P8686 [蓝桥杯 2019 省 A] 修改数组--并查集 or Set--lower_bound()的解法!!!
P8686 [蓝桥杯 2019 省 A] 修改数组--并查集 题目 并查集解析代码【并查集解】 Set 解法解析lower_bound代码 题目 并查集解析 首先先让所有的f(i)i,即每个人最开始的祖先都是自己,然后就每一次都让轮到那个数的父亲1(…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...
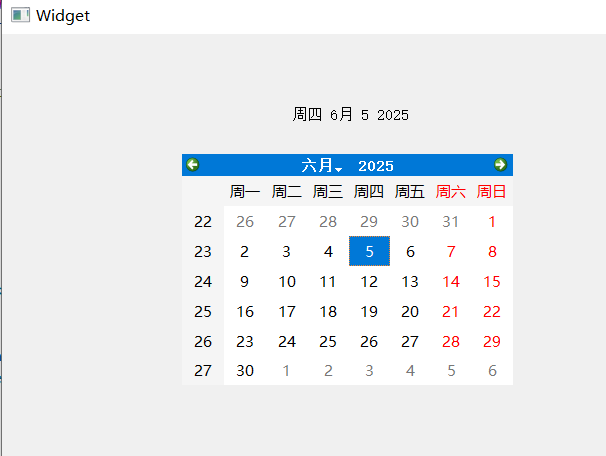
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
