【机器学习实战】七、梯度下降
梯度下降
一、线性回归
线性回归算法推导过程可以基于最小二乘法直接求解,但这并不是机器学习的思想,由此引入了梯度下降方法。本文讲解其中每一步流程与实验对比分析。
1.初始化
import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
2.回归方程
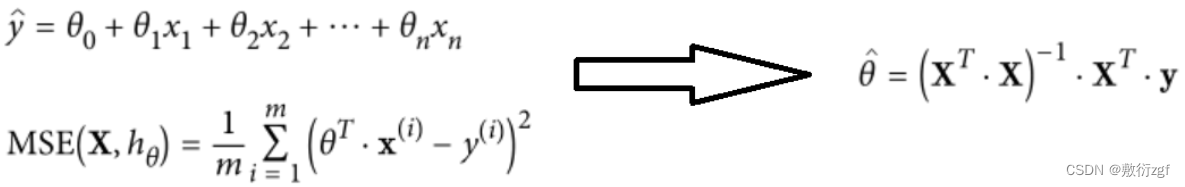
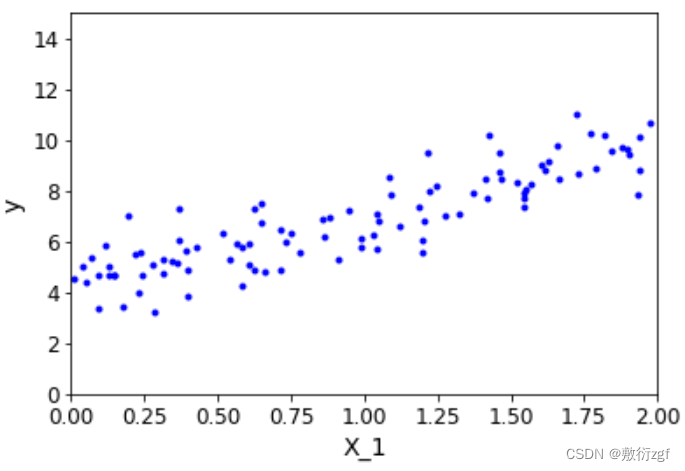
import numpy as np
X = 2*np.random.rand(100,1)
y = 4+ 3*X +np.random.randn(100,1)
plt.plot(X,y,'b.')
plt.xlabel('X_1')
plt.ylabel('y')
plt.axis([0,2,0,15])
plt.show()
X_b = np.c_[np.ones((100,1)),X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)
# 输出 :
array([[4.21509616],[2.77011339]])
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)),X_new]
y_predict = X_new_b.dot(theta_best)
print(y_predict)
# 输出:
array([[4.21509616],[9.75532293]])
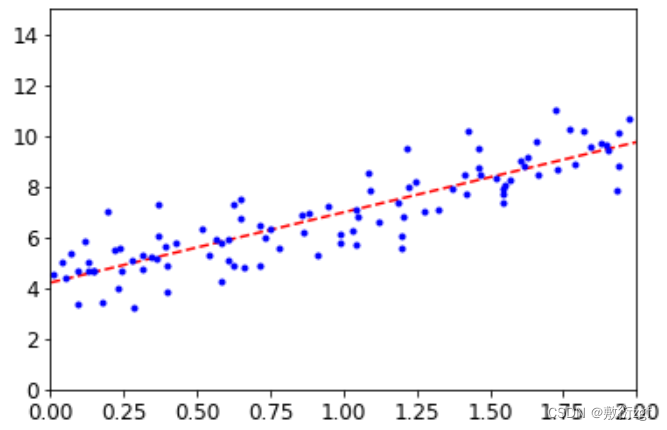
plt.plot(X_new,y_predict,'r--')
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()
二、调用sklearn API
sklearnAPI官网: https://scikit-learn.org/stable/modules/classes.html
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
print (lin_reg.coef_)
print (lin_reg.intercept_)
#
[[2.77011339]]
[4.21509616]
三、梯度下降
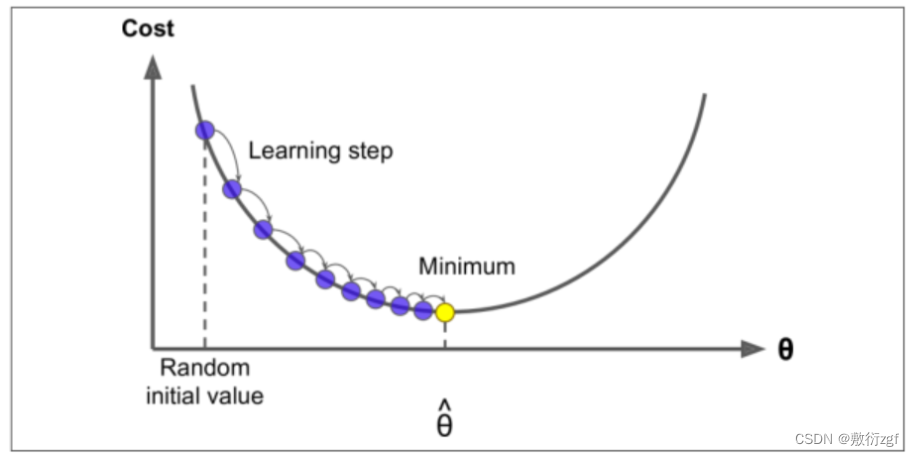
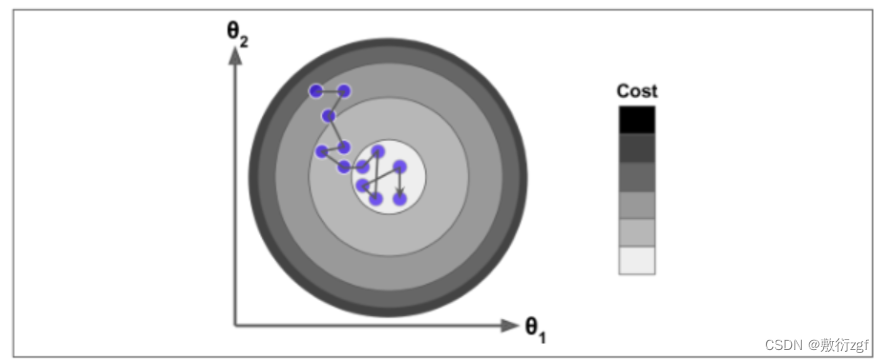
当步长较小时,训练次数较多;
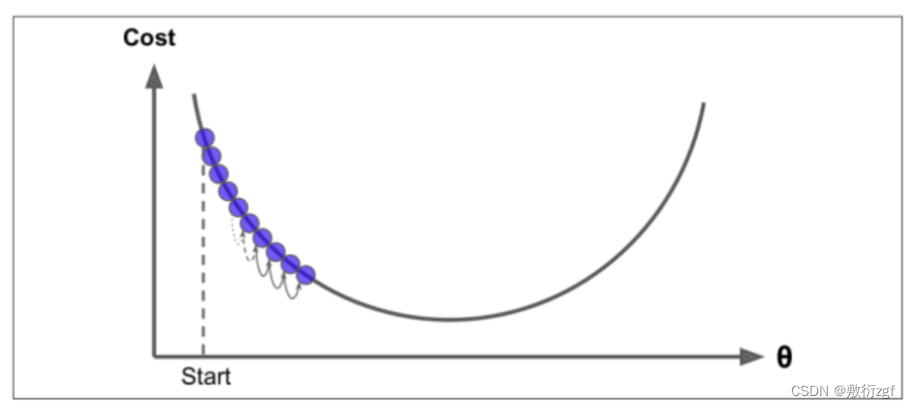
当步长较大时,波动大;
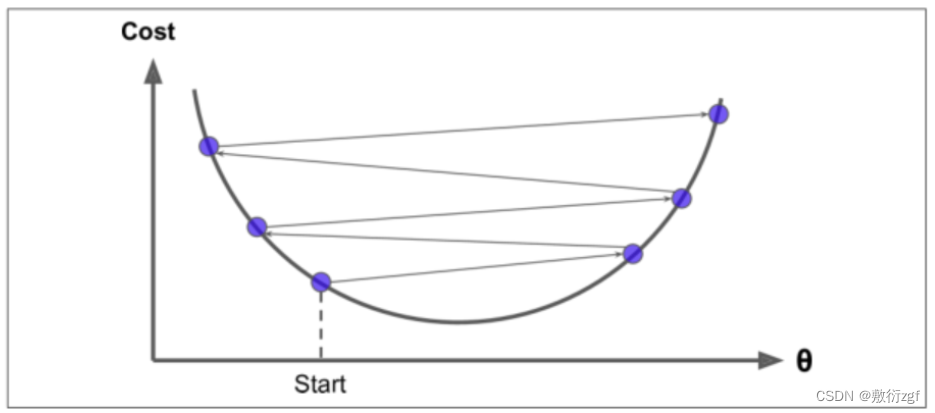
学习率应当尽可能小,随着迭代的进行应当越来越小。
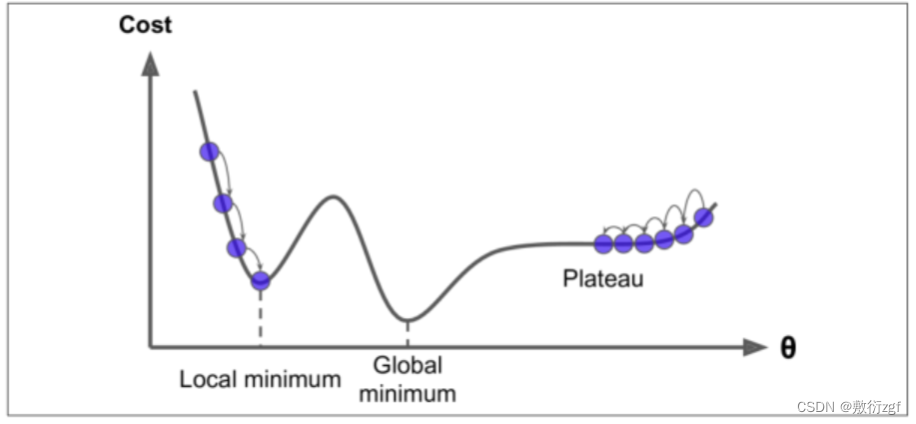
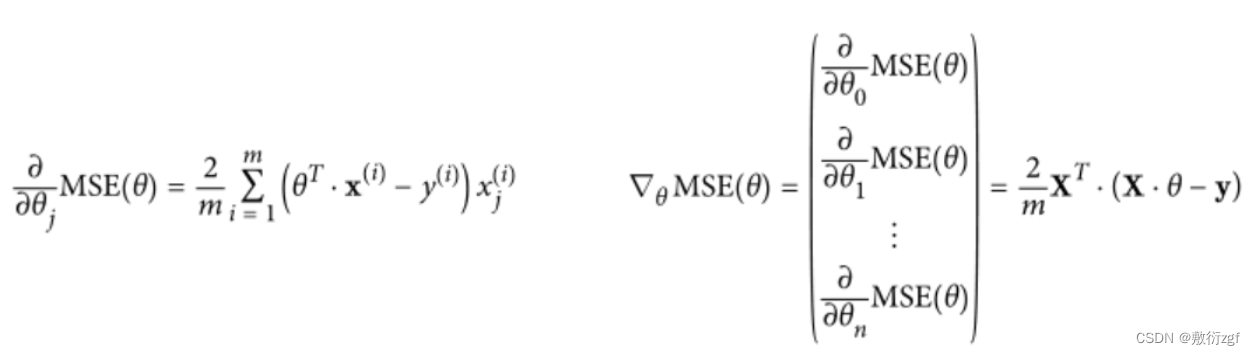
1.批量梯度下降
eta = 0.1 #学习率
n_iterations = 1000 # 迭代次数
m = 100
theta = np.random.randn(2,1) # 随机初始化参数theta
for iteration in range(n_iterations):gradients = 2/m* X_b.T.dot(X_b.dot(theta)-y)theta = theta - eta*gradients
theta
#
array([[4.21509616],[2.77011339]])
X_new_b.dot(theta)
#
array([[4.21509616],[9.75532293]])
theta_path_bgd = []
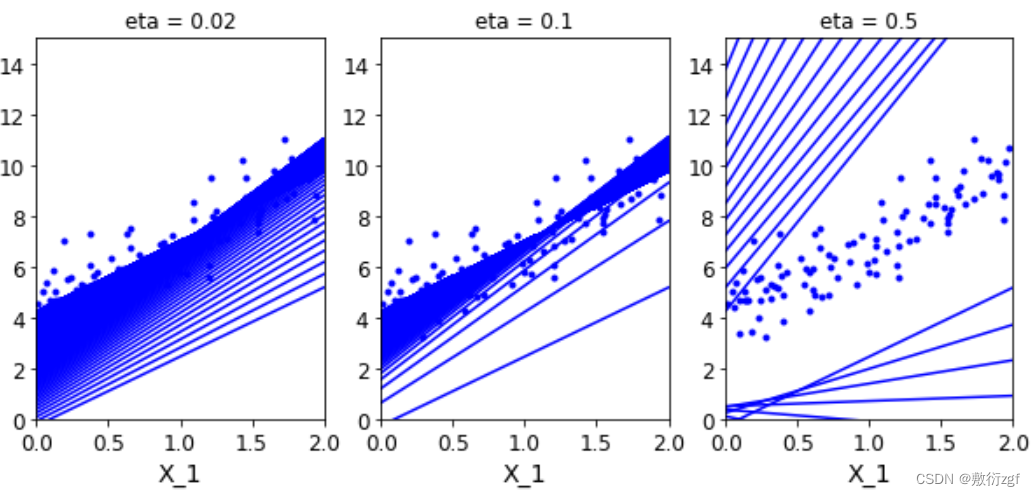
def plot_gradient_descent(theta,eta,theta_path = None):m = len(X_b)plt.plot(X,y,'b.')n_iterations = 1000for iteration in range(n_iterations):y_predict = X_new_b.dot(theta)plt.plot(X_new,y_predict,'b-')gradients = 2/m* X_b.T.dot(X_b.dot(theta)-y)theta = theta - eta*gradientsif theta_path is not None:theta_path.append(theta)plt.xlabel('X_1')plt.axis([0,2,0,15])plt.title('eta = {}'.format(eta))
theta = np.random.randn(2,1)plt.figure(figsize=(10,4))
plt.subplot(131)
plot_gradient_descent(theta,eta = 0.02)
plt.subplot(132)
plot_gradient_descent(theta,eta = 0.1,theta_path=theta_path_bgd)
plt.subplot(133)
plot_gradient_descent(theta,eta = 0.5)
plt.show()
2.随机梯度下降
theta_path_sgd=[]
m = len(X_b)
np.random.seed(42)
n_epochs = 50
t0 = 5
t1 = 50def learning_schedule(t):return t0/(t1+t)
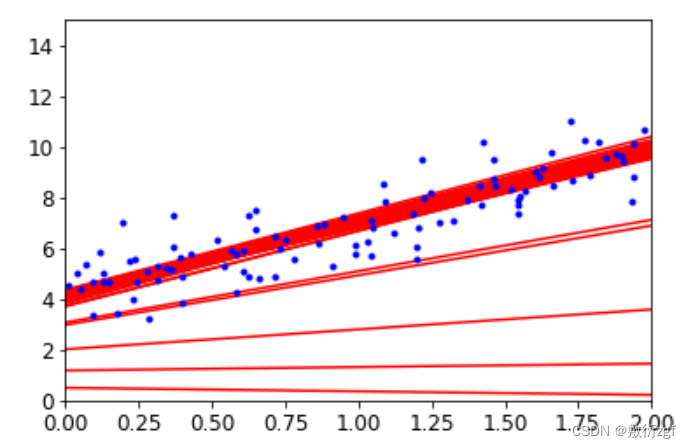
theta = np.random.randn(2,1)for epoch in range(n_epochs):for i in range(m):if epoch < 10 and i<10:y_predict = X_new_b.dot(theta)plt.plot(X_new,y_predict,'r-')random_index = np.random.randint(m)xi = X_b[random_index:random_index+1]yi = y[random_index:random_index+1]gradients = 2* xi.T.dot(xi.dot(theta)-yi)eta = learning_schedule(epoch*m+i)theta = theta-eta*gradientstheta_path_sgd.append(theta)plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()
3.MiniBatch梯度下降
theta_path_mgd=[]
n_epochs = 50
minibatch = 16
theta = np.random.randn(2,1)
t0, t1 = 200, 1000
def learning_schedule(t):return t0 / (t + t1)
np.random.seed(42)
t = 0
for epoch in range(n_epochs):shuffled_indices = np.random.permutation(m)X_b_shuffled = X_b[shuffled_indices]y_shuffled = y[shuffled_indices]for i in range(0,m,minibatch):t+=1xi = X_b_shuffled[i:i+minibatch]yi = y_shuffled[i:i+minibatch]gradients = 2/minibatch* xi.T.dot(xi.dot(theta)-yi)eta = learning_schedule(t)theta = theta-eta*gradientstheta_path_mgd.append(theta)
theta
#
array([[4.25490684],[2.80388785]])
四、3种策略的对比实验
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(12,6))
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],'r-s',linewidth=1,label='SGD')
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],'g-+',linewidth=2,label='MINIGD')
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],'b-o',linewidth=3,label='BGD')
plt.legend(loc='upper left')
plt.axis([3.5,4.5,2.0,4.0])
plt.show()
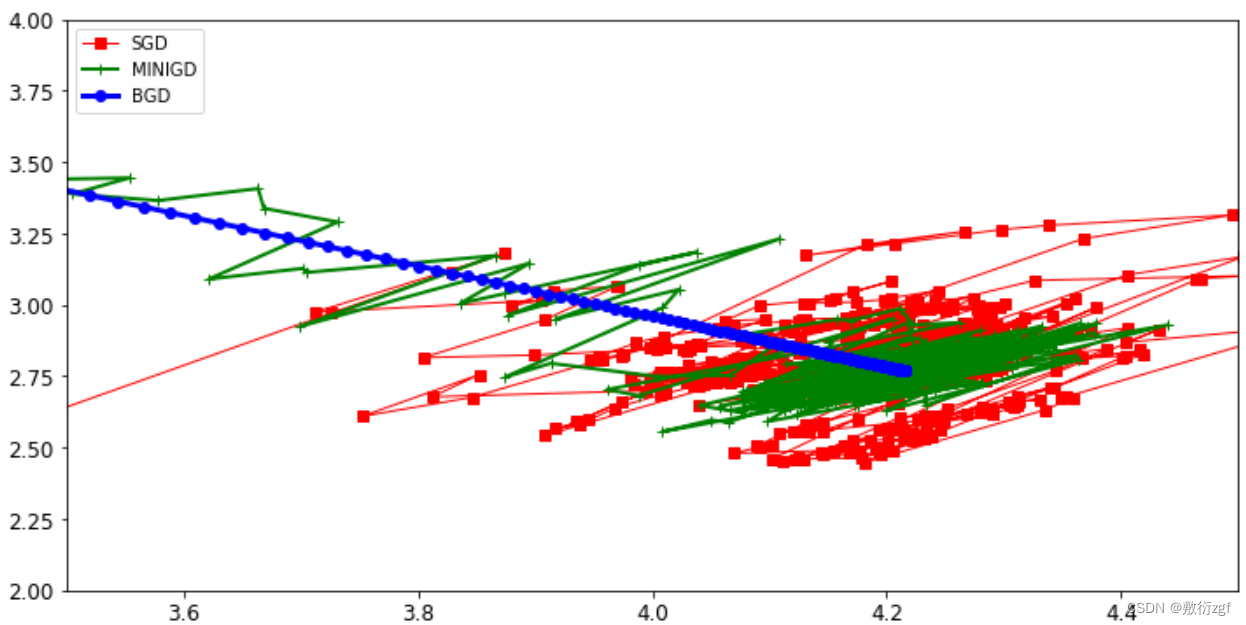
实际当中用minibatch比较多,一般情况下选择batch数量应当越大越好。
相关文章:

【机器学习实战】七、梯度下降
梯度下降 一、线性回归 线性回归算法推导过程可以基于最小二乘法直接求解,但这并不是机器学习的思想,由此引入了梯度下降方法。本文讲解其中每一步流程与实验对比分析。 1.初始化 import numpy as np import os %matplotlib inline import matplotli…...

什么是极速文件传输,极速文件传输如何进行大文件传输
当谈到大文件传输时,人们总是担心大数据文件的大小以及将它们从一个位置交换到另一个位置需要多长时间。由于数据捕获高分辨率视频和图像的日益复杂,文件的大小不断增加。数据工作流在地理上变得越来越分散。在一个位置生成的文件在其他位置处理或使用。…...

Spring Boot 日志
目录 1.概述 2.切换日志实现 3.使用 3.1.日志级别 3.3.日志离线 3.4.详细定制 1.概述 由一些历史原因,JAVA领域存在有很多日志框架,如Log4j、Logback、log4j2。 log4j是Java日志框架的元老,在log4j被Apache Foundation收入门下之后&a…...

好用的研发管理看板工具有哪些?10款主流看板管理软件盘点
10大企业看板工具软件:1.软件开发项目看板 PingCode;2.通用看板软件 Worktile;3.开源看板软件 Wekan;4.免费看板软件 Trello;5.个人和小团队的看板软件 Todoist ;6.开源免费看 Kanboard;7.面向个…...
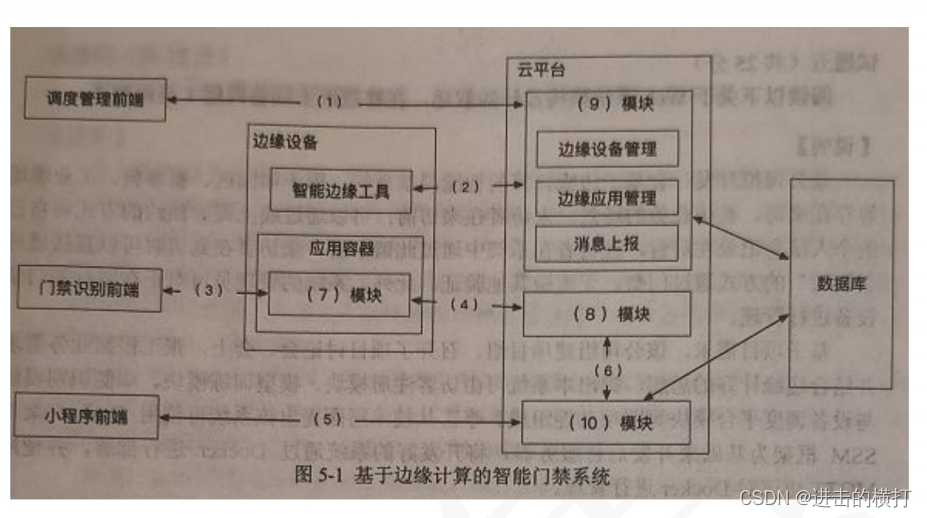
【软考系统架构设计师】2022下案例分析历年真题
【软考系统架构设计师】2022下案例分析历年真题 【软考系统架构设计师】2022下案例分析历年真题【软考系统架构设计师】2022下案例分析历年真题2022下案例分析历年真题第一题(25分)2022下案例分析历年真题第二题(25分)2022下案例分…...

Java skill - @JsonAlias 和 @JsonProperty
Java skill - JsonAlias 和 JsonPropertyJava skill系列目录:JsonAlias 和 JsonProperty使用 JsonProperty 的麻烦场景:使用 JsonAlias 应对麻烦场景:Java skill系列目录: 【Java skill - 统计耗时用StopWatch】 【Java skill - …...
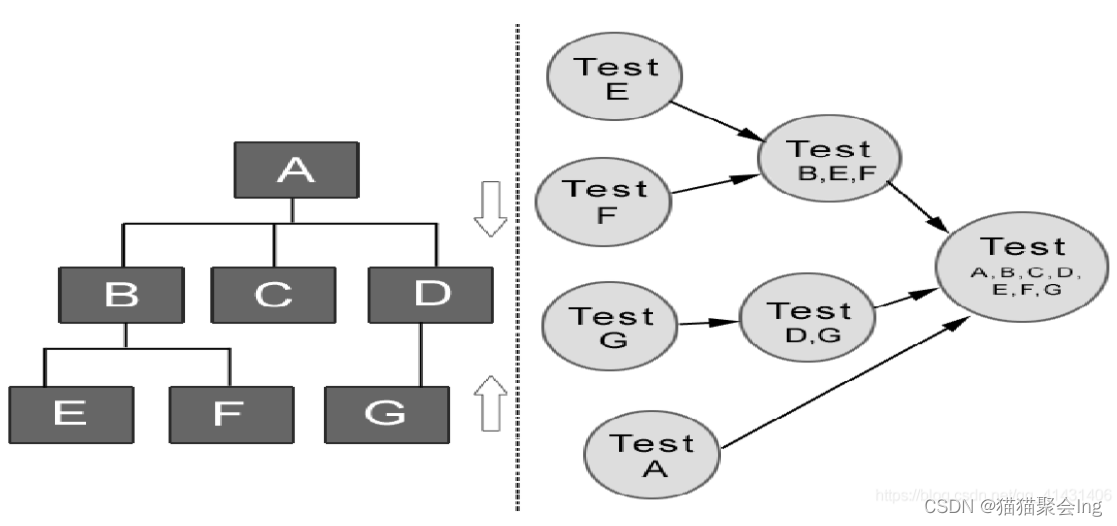
【实际开发18】- 静态 3
目录 1. 调试与评估 2. 单元测试的管理 1. 单元测试的文档 3. 系统集成的模式与方法 1. 集成测试前的准备 2. 集成测试的模式 3. 大棒集成方法 ( Big-bang Integration) 4. 自顶向下和自底向上集成方法 1. 自顶向下法 ( Top-down Integration ) 2. 自底向上法 ( Bott…...

【swagger2】开发api文档
文章目录一、swagger2 简介背景Open API ???swagger2的作用swagger2常用工具组件:二、Springfox三、springBoot使用swagger2(简单示例)四、Swagger-UI使用五、配置文件1、配置类:给docket上下文配置api描述信息2、配置类&#…...

Github 上如何提交 pull request
什么是复刻(forking)? 我们可以通过复刻操作将喜爱的仓库保存自己的Github账户中,以便独立地对其进行操作。 通过复刻,我们可以得到包含完整版本历史的目标仓库的实例,之后可以对复刻得到的仓库进行任意操作而不会影响…...

Redis面试知识
概述 Redis 是速度非常快的非关系型(NoSQL)内存键值数据库,可以存储键和五种不同类型的值之间的映射。 键的类型只能为字符串,值支持五种数据类型:字符串、列表、集合、散列表、有序集合。 Redis 支持很多特性,例如将内存中的数据持久化到硬盘中,使用复制来扩展读性能…...

Spring面试重点(四)——Spring事务
Spring事务 事务的方式 spring中使用事务有两种方式,一种是编程式事务,一种是声明式事务。编程式事务推荐使用TransactionTemplate,实现TransactionCallback接口,需要编码实现;声明式事务只需要在函数增加注解Transa…...

♡ — MySQL 存储引擎
MySQL 存储引擎架构 MySQL 存储引擎采用的是插件式架构,支持多种存储引擎,我们甚至可以为不同的数据库设置不同的存储引擎以适应不同场景的需要;存储引擎是基于表的,而不是数据库。 MyISAM 和 InnoDB 的区别 MySQL 5.5 之前&am…...
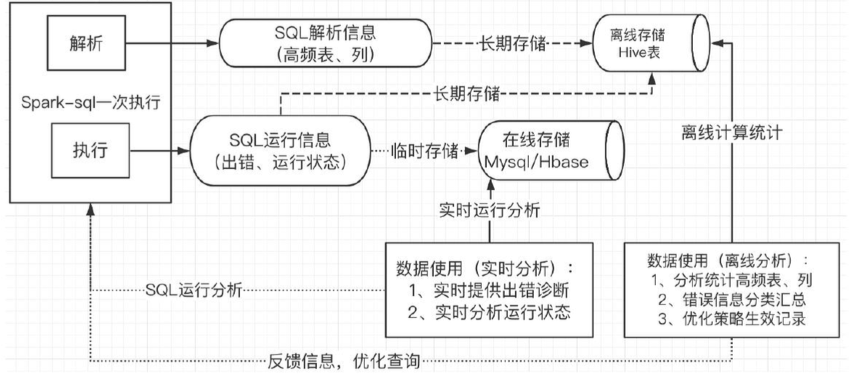
大数据技术架构(组件)34——Spark:Spark SQL--Optimize
2.2.3、Optimize2.2.3.1、SQL3.3.1.1、RB1、Join选择在Hadoop中,MR使用DistributedCache来实现mapJoin。即将小文件存放到DistributedCache中,然后分发到各个Task上,并加载到内存中,类似于Map结构,然后借助于Mapper的迭…...
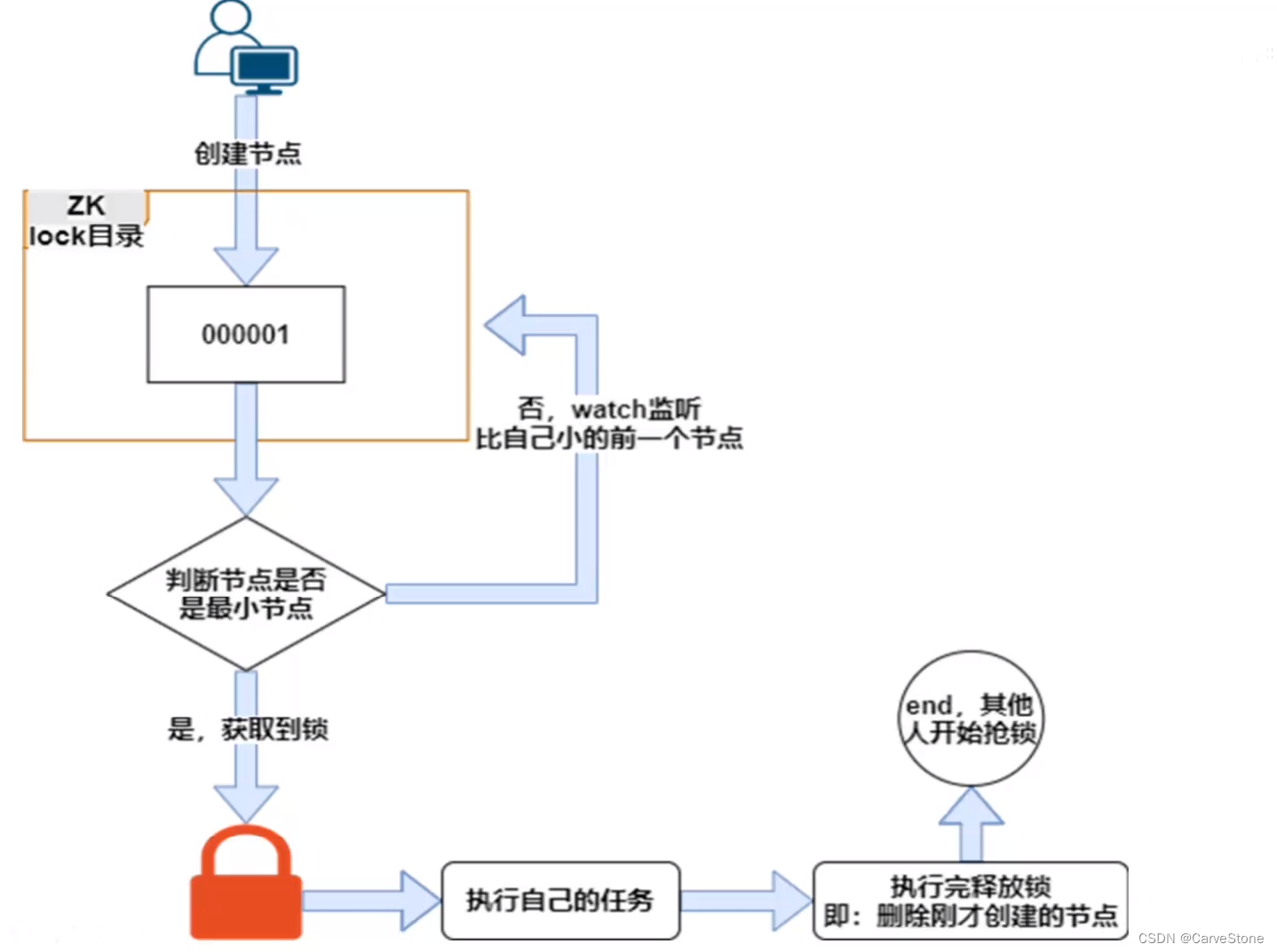
Zookeeper实现分布式锁
文章目录ZK节点类型watch监听机制Zookeeper实现分布式锁锁原理创建锁的过程释放锁的过程ZK锁的种类代码实现Zookeeper是一个开源的分布式协调服务,是一个典型的分布式数据一致性解决方案。 分布式应用程序可以基于Zookeeper实现诸如数据发布/订阅,负载均…...

MFC 添加重新启动管理器支持
重启管理器是添加到 Visual Studio for Windows Vista 或更高版本操作系统的功能 如果发生意外关闭或重启,重新启动管理器将为你的应用程序添加支持。 重新启动管理器的行为取决于应用程序的类型。 如果你的应用程序是文档编辑器,则重新启动管理器让应用…...

一文带你深刻的进入Python,并且了解Python的优缺点
最近几年Python被吹的神乎其神,很多同学都不清楚Python到底能干什么?就盲目去学习Python,今天我就Python的应用领域来简单盘点一下,让想学习Python 的同学找对方向不迷茫。 2. Python 的特点 这里就谈谈自己的看法,首先 Python是…...

别具一格,原创唯美浪漫情人节表白专辑,(复制就可用)(html5,css3,svg)表白爱心代码(4)
别具一格,独此一家,原创唯美浪漫情人节表白专辑 不一样的惊喜哦~!(html5,css3,svg)表白爱心代码(复制就可用)(4) 目录 款式四:时光的记忆款 1、拷贝完整源代码 2、更新时光盒所…...

编译原理—翻译方案、属性栈代码
系列文章戳这里👇 什么是上下文无关文法、最左推导和最右推导如何判断二义文法及消除文法二义性何时需要消除左递归什么是句柄、什么是自上而下、自下而上分析什么是LL(1)、LR(0)、LR(1)文法、LR分析表LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系编译原理第三章习…...

链表
一、从尾到头打印链表题目:输入一个链表,按链表从尾到头的顺序返回一个ArrayList。解题思路:使用栈作为中转,可以实现倒置打印classSolution { public:vector<int> printListFromTailToHead(ListNode* head){//使用栈完成中…...

CSS 样式优先级
CSS 样式优先级决定了最终呈现在浏览器中的样式是哪一组样式,在多组样式中有冲突时,最终呈现在浏览器中的样式是具有最高优先级的样式。 CSS 样式优先级顺序如下: 内联样式 > 内部样式 > 外部样式 !important > 内联样式 > ID…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
