编译原理—翻译方案、属性栈代码
系列文章戳这里👇
- 什么是上下文无关文法、最左推导和最右推导
- 如何判断二义文法及消除文法二义性
- 何时需要消除左递归
- 什么是句柄、什么是自上而下、自下而上分析
- 什么是LL(1)、LR(0)、LR(1)文法、LR分析表
- LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系
- 编译原理第三章习题
- 词法分析、构建DFA、上下文无关文法、LL(1)分析、提取正规式
- 证明LL(1)、SLR(1)、LALR(1)文法
- 翻译方案、属性栈代码
编译原理—翻译方案、属性栈代码
- 系列文章戳这里👇
- 属性栈代码:
- 举个栗子
- 引入标记非终结符模拟继承属性的计算
文法如下:
S→(L)∣aL→L,S∣SS → (L) | a\\ L → L, S | S S→(L)∣aL→L,S∣S
(a) 写一个翻译方案,它输出每个 a 的嵌套深度。例如,对于句子 (a, (a, a)),输出的结果是 1 2 2。
文法符号S,L继承属性depth表示嵌套深度,则翻译方案如下:
S′→{S.depth=0}SS→({L.depth=S.depth}L)S→a{print(S.depth)}L→{L1.depth=L.depth,S.depth=L.depth}L1,SL→{S.depth=L.depth}S\begin{aligned} S'&→\{S.depth=0\}S\\ S&→(\{L.depth = S.depth\}L)\\ S&→a\{print(S.depth)\}\\ L&→\{L_1.depth=L.depth,S.depth=L.depth\}L_1,S\\ L&→\{S.depth=L.depth\}S \end{aligned} S′SSLL→{S.depth=0}S→({L.depth=S.depth}L)→a{print(S.depth)}→{L1.depth=L.depth,S.depth=L.depth}L1,S→{S.depth=L.depth}S
属性栈代码,由于 属性栈上仅能存放综合属性(后文有详细介绍),所以需要引入标记非终结符P、Q、R,及其综合属性s,继承属性i,模拟继承属性的计算,则栈代码如下:
S′→{S.depth=P.s}PSP→ϵ{P.s=0}Stack[ntop]=0S→({Q.i=S.depth,L.depth=Q.s}QL)Q→ϵ{Q.s=Q.i+1}Stack[ntop]=Stack[top−1]+1S→a{print(S.depth)}print(Stack[top−1])L→{L1.depth=L.depth,R.i=L.depth,S.depth=R.s}L1,RSR→ϵ{R.s=R.i}Stack[ntop]=Stack[top−2]L→{S.depth=L.depth}S\begin{aligned} S'&→\{S.depth=P.s\}PS\\ P&→\epsilon\{P.s=0\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]=0\\ S&→(\{Q.i=S.depth,L.depth = Q.s\}QL)\\ Q&→\epsilon\{Q.s=Q.i+1\}\ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]= Stack[top-1]+1\\ S&→a\{print(S.depth)\}\ \ \ \ \ \ \ \ \ \ print(Stack[top-1])\\ L&→\{L_1.depth=L.depth,R.i=L.depth,S.depth=R.s\}L_1,RS\\ R&→\epsilon\{R.s=R.i\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop] = Stack[top-2]\\ L&→\{S.depth=L.depth\}S \end{aligned} S′PSQSLRL→{S.depth=P.s}PS→ϵ{P.s=0} Stack[ntop]=0→({Q.i=S.depth,L.depth=Q.s}QL)→ϵ{Q.s=Q.i+1} Stack[ntop]=Stack[top−1]+1→a{print(S.depth)} print(Stack[top−1])→{L1.depth=L.depth,R.i=L.depth,S.depth=R.s}L1,RS→ϵ{R.s=R.i} Stack[ntop]=Stack[top−2]→{S.depth=L.depth}S
(b) 写一个翻译方案,它打印出每个 a 在句子中是第几个字符。例如,当句子是 (a, (a, (a, a),(a)))时,打印的结果是 2 5 8 10 14。
使用综合属性out表示当前文法符号推出的字符总数,基础属性before表示该文法符号前有多少个字符,则翻译方案如下:
S′→{S.before=0}SS→{L.before=S.before}(L){S.out=L.out+2}S→a{S.out=1;print(S.before+1)}L→{L1.before=L.before,S.before=L.before+L1.out+1}L1,S{L.out=L1.out+S.out+1}L→{S.before=L.before}S{L.out=S.out}\begin{aligned} S'&→\{S.before=0\}S\\ S&→\{L.before = S.before\} \\&\ \ \ \ \ \ \ \ \ \ \ (L) \\&\ \ \ \ \ \ \ \ \ \ \ \{S.out=L.out+2\}\\ S&→a\{S.out=1;print(S.before+1)\}\\ L&→\{L_1.before=L.before, \\&\ \ \ \ \ \ \ \ \ \ \ S.before=L.before+L_1.out+1\} \\&\ \ \ \ \ \ \ \ \ \ \ L_1,S \\&\ \ \ \ \ \ \ \ \ \ \ \{L.out=L_1.out+S.out+1\}\\ L&→\{S.before=L.before\}S\{L.out=S.out\} \end{aligned} S′SSLL→{S.before=0}S→{L.before=S.before} (L) {S.out=L.out+2}→a{S.out=1;print(S.before+1)}→{L1.before=L.before, S.before=L.before+L1.out+1} L1,S {L.out=L1.out+S.out+1}→{S.before=L.before}S{L.out=S.out}
同理上述翻译方案栈代码如下:
S′→{S.before=P.s}PSP→ϵ{P.s=0}Stack[ntop]=0S→({Q.i=S.before,L.before=Q.s}QL){S.out=L.out+2}Q→ϵ{Q.s=Q.i+1}Stack[ntop]=Stack[top−1]+1S→a{print(S.before)}print(Stack[top−1])L→{L1.before=L.before,R.i=L.before+L1.out+1,S.before=R.s}L1,RS{L.out=L1.out+S.out+1}Stack[ntop]=Stack[top−3]+Stack[top]+1R→ϵ{R.s=R.i}Stack[ntop]=Stack[top−2]+Stack[top−1]+1L→{S.before=L.before}S{L.out=S.out}Stack[ntop]=Stack[top]\begin{aligned} S'&→\{S.before=P.s\}PS\\ P&→\epsilon\{P.s=0\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]=0\\ S&→(\{Q.i = S.before,L.before = Q.s\} \\&\ \ \ \ \ \ \ \ \ \ \ QL) \\&\ \ \ \ \ \ \ \ \ \ \ \{S.out=L.out+2\} \\ Q&→\epsilon\{Q.s=Q.i+1\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]= Stack[top-1]+1\\ S&→a\{print(S.before)\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ print(Stack[top-1])\\ L&→\{L_1.before=L.before, \\&\ \ \ \ \ \ \ \ \ \ \ R.i=L.before+L_1.out+1, \\&\ \ \ \ \ \ \ \ \ \ \ S.before=R.s\} \\&\ \ \ \ \ \ \ \ \ \ \ L_1,RS \\&\ \ \ \ \ \ \ \ \ \ \ \{L.out=L_1.out+S.out+1\} \ \ \ \ \ \ \ \ \ Stack[ntop]=Stack[top-3]+Stack[top]+1 \\ R&→\epsilon\{R.s=R.i\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop] = Stack[top-2]+Stack[top-1]+1\\ L&→\{S.before=L.before\}S \\& \ \ \ \ \ \ \ \{L.out=S.out\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]=Stack[top] \end{aligned} S′PSQSLRL→{S.before=P.s}PS→ϵ{P.s=0} Stack[ntop]=0→({Q.i=S.before,L.before=Q.s} QL) {S.out=L.out+2}→ϵ{Q.s=Q.i+1} Stack[ntop]=Stack[top−1]+1→a{print(S.before)} print(Stack[top−1])→{L1.before=L.before, R.i=L.before+L1.out+1, S.before=R.s} L1,RS {L.out=L1.out+S.out+1} Stack[ntop]=Stack[top−3]+Stack[top]+1→ϵ{R.s=R.i} Stack[ntop]=Stack[top−2]+Stack[top−1]+1→{S.before=L.before}S {L.out=S.out} Stack[ntop]=Stack[top]
属性栈代码:
- 如何在自底向上分析中计算继承属性?
- 属性栈上仅能存放综合属性
- 分析栈中符号的继承属性
- 属性copy规则
如果,A→XYA→XYA→XY,有语义规则Y.i:=X.sY.i := X.sY.i:=X.s,
翻译方案可写为:
A→X{Y.i:=X.s}YA → X \{ Y.i := X.s \} YA→X{Y.i:=X.s}Y
- 属性copy规则
- 从句柄下面取继承属性!

举个栗子
有如下文法与翻译方案
D→T { L.in := T.type } L T→int { T.type := integer }T→real { T.type := real }L→ { L1.in := L.in }L1 , id {addtype(id.entry, L.in) }L→id { addtype(id.entry, L.in) }
对于输入串:int p,q,r 分析过程如下:


引入标记非终结符模拟继承属性的计算


相关文章:

编译原理—翻译方案、属性栈代码
系列文章戳这里👇 什么是上下文无关文法、最左推导和最右推导如何判断二义文法及消除文法二义性何时需要消除左递归什么是句柄、什么是自上而下、自下而上分析什么是LL(1)、LR(0)、LR(1)文法、LR分析表LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系编译原理第三章习…...

链表
一、从尾到头打印链表题目:输入一个链表,按链表从尾到头的顺序返回一个ArrayList。解题思路:使用栈作为中转,可以实现倒置打印classSolution { public:vector<int> printListFromTailToHead(ListNode* head){//使用栈完成中…...

CSS 样式优先级
CSS 样式优先级决定了最终呈现在浏览器中的样式是哪一组样式,在多组样式中有冲突时,最终呈现在浏览器中的样式是具有最高优先级的样式。 CSS 样式优先级顺序如下: 内联样式 > 内部样式 > 外部样式 !important > 内联样式 > ID…...

SpingMVC获取请求参数
通过ServletAPI获取请求参数将HttpServletRequest作为控制器方法的形参,此时HttpServletRequest类型的参数表示封装了当前请求的请求报文的对象。html<form th:action"{/param/servletAPI}" method"post">用户名:<input ty…...
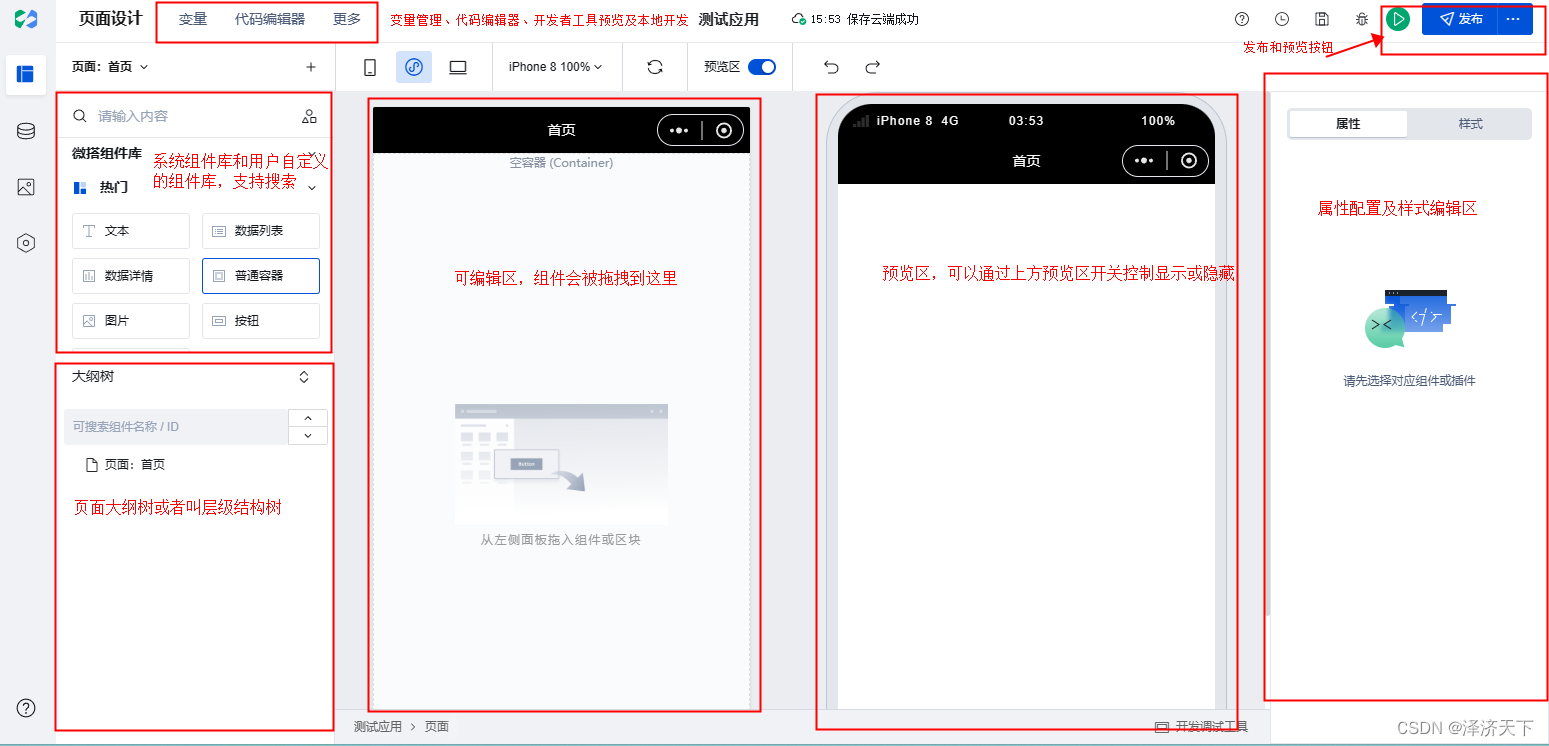
微搭使用笔记(二)微搭低代码平台介绍及基础使用
概述 官网地址: 官网 官方文档: 官方文档 FAQ: FAQ 腾讯云微搭低代码是一个高性能的低代码开发平台,用户可通过拖拽式开发,可视化配置构建 PC Web、H5 和小程序应用。支持打通企业内部数据,轻松实现企业微信管理、工…...

CountDownLatch的定义、使用 、原理
一、定义 CountDownLatch的作用很简单,就是一个或者一组线程在开始执行操作之前,必须要等到其他线程执行完才可以。我们举一个例子来说明,在考试的时候,老师必须要等到所有人交了试卷才可以走。此时老师就相当于等待线程ÿ…...
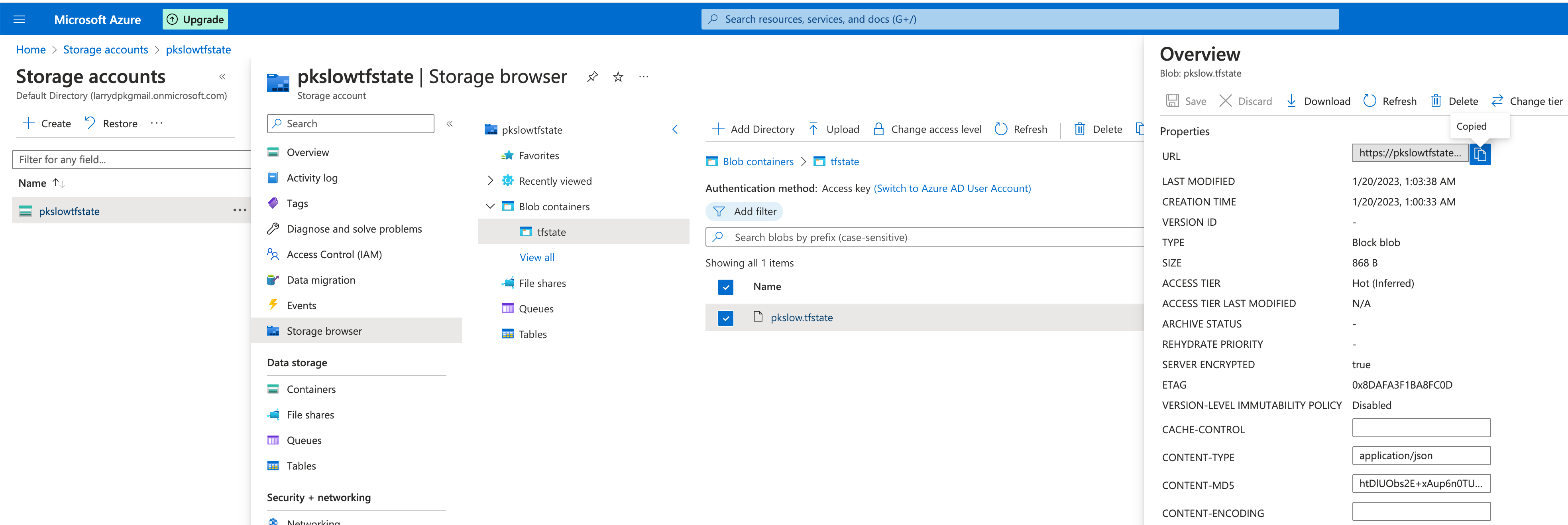
《Terraform 101 从入门到实践》 Terraform在公有云Azure上的应用
《Terraform 101 从入门到实践》这本小册在南瓜慢说官方网站和GitHub两个地方同步更新,书中的示例代码也是放在GitHub上,方便大家参考查看。 简介 Azure是微软的公有云,它提供了一些免费的资源,具体可以查看: https:/…...

别具一格,原创唯美浪漫情人节表白专辑,(复制就可用)(html5,css3,svg)表白爱心代码(3)
别具一格,原创唯美浪漫情人节表白专辑, (复制就可用)(html5,css3,svg)表白爱心代码(3) 目录 款式三:心形实时显示认识多长时间桃花飞舞(猫咪)款 1、拷贝完整源代码 2、拷贝完整js代码 3、修改时间 4、…...

Linux 删除修改日期大于某一天的文件
在服务器运维过程中,我们往往会产生大量的日志文件. 如果日志文件命名能看出日志产生的时间,这些文件是很好删除的. 但有时,我们可能有成千上万的没有命名规律日志文件 下面的方法可以根据日志最后修改时间 批量删除这些文件 先给出完整命令: find /mydir -mtime 10 -name &…...

【算法题】1845. 座位预约管理系统
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 题目: 请你设计一个管理 n 个座位预约的系…...

【专业认知】保研北大金融 / 入职腾讯产品经理
2023.02.11 一. 朱博文学长分享——关于大学生活的一点思考 1. 自我介绍 大数据18级 经济学双学位 保研至北大金融硕士 “多思考、多感受、兼听则明” 2. 大学生活 2.1 为什么要上大学 1:追求美好生活的需要 “美好”难以量化,因为每个人对生活…...

OpenHarmony使用Socket实现一个UDP客户端详解
一、前言 我们在这里介绍Socket的使用,是为了后面的一篇文章实现设备配网做铺垫。 二、示例详解 点击获取BearPi-HM_Nano源码 ,以D3_iot_udp_client为例: 示例本身很简单,只需要修改 udp_client_demo.c 的2处代码,就能测试了: //连接WIFI,参数1是:WIFI名称,参数2是:…...
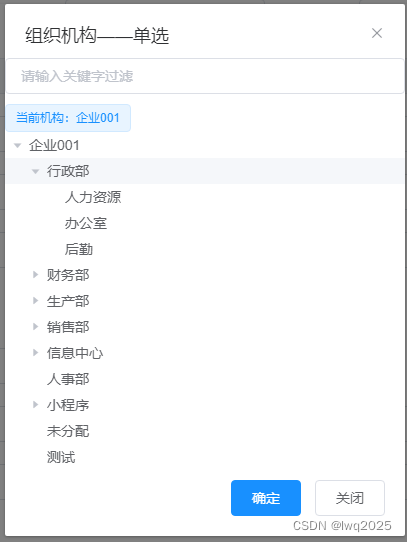
使用VUE自定义组件封装部门选择功能
背景 照惯例,先交待下背景,从真实需求出发,讲述实现效果、设计思路和实现方式。 软件系统中,会有一些常见常用的选择功能,如部门选择、人员选择等,用于填报表单,使用频率很高。直接使用一方面会…...
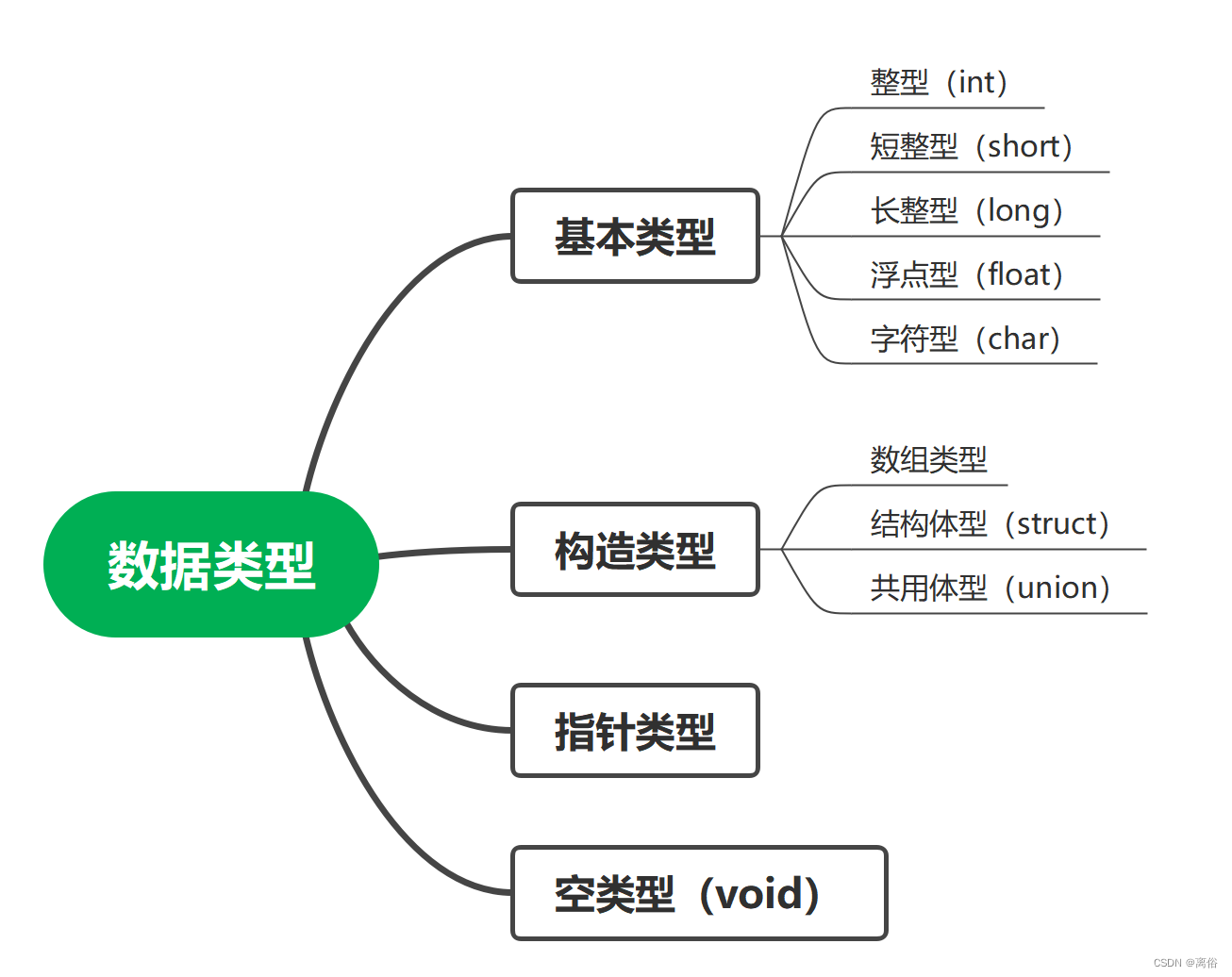
C语言基础应用(一)数据类型
一、数据类型 1、数据类型的分类 2、常量 常量是固定值,在程序执行期间不会改变。这些固定的值,又叫做字面量。 2.1 常量举例 // 整型常量 举例 /*718 十进制0213 八进制0x4b 十六进制30u 无符号整数30l 长整型30ul 无符号长整型*/ // 浮点常量…...

算法笔记(三)—— 桶排序及排序总结
堆 逻辑上是一棵完全二叉树(依次遍满或者全满)。 数组可以转为完全二叉树,完全二叉树某结点左孩子(2*i1),右孩子(i*22),父结点((i-1/)2),根节点的父还是自己。 如何将数组转化为堆(大根堆&…...
Linux入门篇(一)
Linux前言Linux初探Linux内核GNU实用工具shellLinux发行版bash shell 基础Linux文件系统Linux文件操作命令前言 在阅读诸如docker之类的书的时候,经常碰到Linux的知识。同时,大部分的盲区也是在Linux方面。因此就想稍微了解一下这个广为人使用的操作系统…...

HTTPSHandler SSL Error
我在服务器ubuntu中,尝试使用pip3,但是出现下面的报错 ImportError: cannot import name HTTPSHandler 通过查询资料,发现报错的原因是,该pip3.5中没有安装好openssl. 我尝试在python3.5中使用import ssl, 确实是会显示下面的报错…...

基于Android的高校食堂餐厅配送系统
需求信息: 商家客户端: 1:登录注册:用户可以通过自己的信息进行账号的注册 2:发布菜单:发布自己经营的美食信息 3:用户订单:查看用户的购买订单 4:订单配送:对…...

Java设计模式-02工厂模式
为什么需要工厂模式,其作用什么?如何实现,代码演示解析优缺点。Q1:为什么需要工厂模式?工厂模式的作用(优点)是什么? 解耦。把对象的创建和使用的过程分开。就是Class A 想调用 Class B ,那么A只是调用B的…...
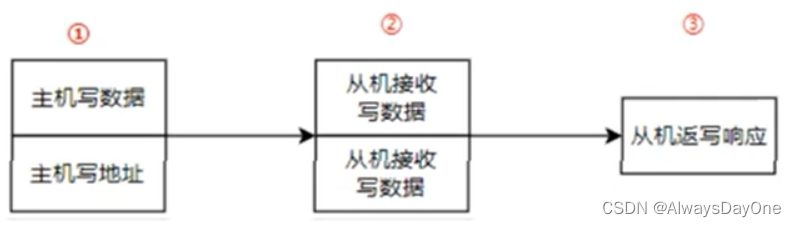
AXI-Lite 学习笔记
AXI-Lite 学习笔记 参考 FPGA:AXI_Lite总线基础2-1]、第二节 AXI总线介绍、ZYNQ PL与PS交互专题_哔哩哔哩_bilibili AXI-Lite总线系列1 - 基础知识_哔哩哔哩_bilibili AXI4 介绍 AXI4 是ARM公司提出的一种片内总线,描述了主从设备之间的数据传输方式。主…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
