通过矩阵从整体角度搞懂快速傅里叶变换原理
离散傅里叶变换公式
公式
f[k]=∑n=0N−1g[n]e−i(2π/N)kn,其中(0<=n<N)f[k]=\sum_{n=0}^{N-1}g[n]e^{-i(2\pi/N)kn}, 其中(0<=n<N) f[k]=n=0∑N−1g[n]e−i(2π/N)kn,其中(0<=n<N)
逆变换公式
g[n]=1N∑k=0N−1f[k]ei(2π/N)kn,其中(0<=k<N)g[n]=\frac{1}{N}\sum_{k=0}^{N-1}f[k]e^{i(2\pi/N)kn}, 其中(0<=k<N) g[n]=N1k=0∑N−1f[k]ei(2π/N)kn,其中(0<=k<N)
快速傅里叶变换
从以上公式看,如果直接按照公式来求离散傅里叶变换,其时间复杂度是O(N^2)
快速傅里叶变换就是一种能在O(n*log(n))时间复杂度内进行傅里叶变换及其逆变换的算法
离散傅里叶变换公式矩阵表示
令
G=[g[0]g[1]⋮g[n−1]]F=[f[0]f[1]⋮f[n−1]]G= \begin{bmatrix} g[0] \\ g[1] \\ \vdots \\ g[n-1] \end{bmatrix} \\\ \\\ F= \begin{bmatrix} f[0] \\ f[1] \\ \vdots \\ f[n-1] \end{bmatrix} \\\ G=g[0]g[1]⋮g[n−1] F=f[0]f[1]⋮f[n−1]
E[i]=[e−i(2π/N)∗0∗0e−i(2π/N)∗0∗1⋯e−i(2π/N)∗0∗(n−1)e−i(2π/N)∗1∗095⋯e−i(2π/N)∗1∗(n−1)⋮⋮⋱⋱⋮⋮⋱e−i(2π/N)∗(n−1)∗(n−1)]E[i]=\begin{bmatrix} e^{-i(2\pi/N)*0*0} & e^{-i(2\pi/N)*0*1} & \cdots & e^{-i(2\pi/N)*0*(n-1)} \\ e^{-i(2\pi/N)*1*0} & 95 & \cdots & e^{-i(2\pi/N)*1*(n-1)} \\ \vdots & \vdots & \ddots & \ddots \\ \vdots & \vdots & \ddots & e^{-i(2\pi/N)*(n-1)*(n-1)} \\ \end{bmatrix} E[i]=e−i(2π/N)∗0∗0e−i(2π/N)∗1∗0⋮⋮e−i(2π/N)∗0∗195⋮⋮⋯⋯⋱⋱e−i(2π/N)∗0∗(n−1)e−i(2π/N)∗1∗(n−1)⋱e−i(2π/N)∗(n−1)∗(n−1)
则离散傅里叶公式可改写为
F=E[i]∗GF=E[i]*G F=E[i]∗G
逆变换可改写为
G=1NE[−i]∗FG=\frac{1}{N}E[-i]*F G=N1E[−i]∗F
注意: E[i]里的 i 是一个变量,i 即正虚数单位,代表正变换,-i 代表逆变换,下同。
递归求解
令
E[i][n]=[e−i(2π/N)∗k∗0e−i(2π/N)∗k∗1…e−i(2π/N)∗k∗(n−1)]E[i][n]0n=[e−i(2π/N)∗k∗0e−i(2π/N)∗k∗2…e−i(2π/N)∗k∗(n−2)]E[i][n]1n=[e−i(2π/N)∗k∗1e−i(2π/N)∗k∗3…e−i(2π/N)∗k∗(n−1)]E[i][n]=\begin{bmatrix} e^{-i(2\pi/N)*k*0} & e^{-i(2\pi/N)*k*1} & \dots & e^{-i(2\pi/N)*k*(n-1)}\\ \end{bmatrix} \\\ \\\ E[i][n]^{0n}=\begin{bmatrix} e^{-i(2\pi/N)*k*0} & e^{-i(2\pi/N)*k*2} & \dots & e^{-i(2\pi/N)*k*(n-2)}\\ \end{bmatrix} \\\ \\\ E[i][n]^{1n}=\begin{bmatrix} e^{-i(2\pi/N)*k*1} & e^{-i(2\pi/N)*k*3} & \dots & e^{-i(2\pi/N)*k*(n-1)}\\ \end{bmatrix} \\ E[i][n]=[e−i(2π/N)∗k∗0e−i(2π/N)∗k∗1…e−i(2π/N)∗k∗(n−1)] E[i][n]0n=[e−i(2π/N)∗k∗0e−i(2π/N)∗k∗2…e−i(2π/N)∗k∗(n−2)] E[i][n]1n=[e−i(2π/N)∗k∗1e−i(2π/N)∗k∗3…e−i(2π/N)∗k∗(n−1)]
则
E[i]=[E[0][n]0nE[0][n]1n⋮⋮E[n−1][n]0nE[n−1][n]1n]\\ E[i]= \begin{bmatrix} E[0][n]^{0n} & E[0][n]^{1n} \\ \vdots & \vdots \\ E[n-1][n]^{0n} & E[n-1][n]^{1n} \\ \end{bmatrix} \\ E[i]=E[0][n]0n⋮E[n−1][n]0nE[0][n]1n⋮E[n−1][n]1n
将E[i]矩阵竖着再切一刀,平分两半,用数学语言描述就是,
令
E00(n/2)=[E[0][n]0n⋮E[n/2−1][n]0n]E01(n/2)=[E[0][n]1n⋮E[n/2−1][n]1n]E10(n/2)=[E[n/2][n]0n⋮E[n−1][n]0n]E11(n/2)=[E[n/2][n]1n⋮E[n−1][n]1n]\\ E_{00(n/2)}= \begin{bmatrix} E[0][n]^{0n} \\ \vdots \\ E[n/2-1][n]^{0n}\\ \end{bmatrix} \\\ \\\ E_{01(n/2)}= \begin{bmatrix} E[0][n]^{1n} \\ \vdots \\ E[n/2-1][n]^{1n}\\ \end{bmatrix} \\\ \\\ E_{10(n/2)}= \begin{bmatrix} E[n/2][n]^{0n} \\ \vdots \\ E[n-1][n]^{0n}\\ \end{bmatrix} \\\ \\\ E_{11(n/2)}= \begin{bmatrix} E[n/2][n]^{1n} \\ \vdots \\ E[n-1][n]^{1n}\\ \end{bmatrix} \\\\ E00(n/2)=E[0][n]0n⋮E[n/2−1][n]0n E01(n/2)=E[0][n]1n⋮E[n/2−1][n]1n E10(n/2)=E[n/2][n]0n⋮E[n−1][n]0n E11(n/2)=E[n/2][n]1n⋮E[n−1][n]1n
于是
E[i]=[E00(n/2)E01(n/2)E10(n/2)E11(n/2)]E[i]=\begin{bmatrix} E_{00(n/2)} & E_{01(n/2)} \\ E_{10(n/2)} & E_{11(n/2)} \\ \end{bmatrix} E[i]=[E00(n/2)E10(n/2)E01(n/2)E11(n/2)]
再令
w[k]=e−i(2π/N)∗kw[k]=e^{-i(2\pi/N)*k} w[k]=e−i(2π/N)∗k
W0(n/2)=[w[0]00…00w[1]0…000w[2]…0⋮⋮⋮⋮0000…w[n/2−1]]W1(n/2)=[w[n/2]00…00w[n/2+1]0…000w[n/2+2]…0⋮⋮⋮⋮0000…w[n−1]]W^{0(n/2)}=\begin{bmatrix} w[0] & 0 & 0 & \dots & 0 \\ 0 & w[1] & 0 & \dots & 0 \\ 0 & 0 & w[2] & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & 0 \\ 0 & 0 & 0 & \dots & w[n/2-1] \\ \end{bmatrix} \\\ \\\ W^{1(n/2)}=\begin{bmatrix} w[n/2] & 0 & 0 & \dots & 0 \\ 0 & w[n/2+1] & 0 & \dots & 0 \\ 0 & 0 & w[n/2+2] & \dots & 0 \\ \vdots & \vdots & \vdots & \vdots & 0 \\ 0 & 0 & 0 & \dots & w[n-1] \\ \end{bmatrix} W0(n/2)=w[0]00⋮00w[1]0⋮000w[2]⋮0………⋮…0000w[n/2−1] W1(n/2)=w[n/2]00⋮00w[n/2+1]0⋮000w[n/2+2]⋮0………⋮…0000w[n−1]
于是
E[i]=[E00(n/2)E01(n/2)E10(n/2)E11(n/2)]=[E00(n/2)W0(n/2)∗E00(n/2)E10(n/2)W1(n/2)∗E10(n/2)]=[E00(n/2)W0(n/2)∗E00(n/2)−E00(n/2)−W1(n/2)∗E00(n/2)]=[E00(n/2)W0(n/2)∗E00(n/2)−E00(n/2)W0(n/2)∗E00(n/2)]E[i] =\begin{bmatrix} E_{00(n/2)} & E_{01(n/2)} \\ E_{10(n/2)} & E_{11(n/2)} \\ \end{bmatrix} \\\ \\\ =\begin{bmatrix} E_{00(n/2)} & W^{0(n/2)}*E_{00(n/2)} \\ E_{10(n/2)} & W^{1(n/2)}*E_{10(n/2)} \\ \end{bmatrix} \\\ \\\ =\begin{bmatrix} E_{00(n/2)} & W^{0(n/2)}*E_{00(n/2)} \\ -E_{00(n/2)} & -W^{1(n/2)}*E_{00(n/2)} \\ \end{bmatrix} \\\ \\\ =\begin{bmatrix} E_{00(n/2)} & W^{0(n/2)}*E_{00(n/2)} \\ -E_{00(n/2)} & W^{0(n/2)}*E_{00(n/2)} \\ \end{bmatrix} E[i]=[E00(n/2)E10(n/2)E01(n/2)E11(n/2)] =[E00(n/2)E10(n/2)W0(n/2)∗E00(n/2)W1(n/2)∗E10(n/2)] =[E00(n/2)−E00(n/2)W0(n/2)∗E00(n/2)−W1(n/2)∗E00(n/2)] =[E00(n/2)−E00(n/2)W0(n/2)∗E00(n/2)W0(n/2)∗E00(n/2)]
上面这一步就是整个转化的核心了。
再往后,令
G0(n/2)=[g[0]g[2]⋮g[n−2]]G1(n/2)=[g[1]g[3]⋮g[n−1]]G^{0(n/2)}= \begin{bmatrix} g[0] \\ g[2] \\ \vdots \\ g[n-2] \end{bmatrix} \\\ \\\ G^{1(n/2)}= \begin{bmatrix} g[1] \\ g[3] \\ \vdots \\ g[n-1] \end{bmatrix} \\\ G0(n/2)=g[0]g[2]⋮g[n−2] G1(n/2)=g[1]g[3]⋮g[n−1]
则
F=GE[i]F=[E00(n/2)W0(n/2)∗E00(n/2)−E00(n/2)W0(n/2)∗E00(n/2)]∗[G0(n/2)G1(n/2)]F=GE[i] \\\ F = \begin{bmatrix} E_{00(n/2)} & W^{0(n/2)}*E_{00(n/2)} \\ -E_{00(n/2)} & W^{0(n/2)}*E_{00(n/2)} \\ \end{bmatrix} * \begin{bmatrix} G^{0(n/2)} \\ G^{1(n/2)} \\ \end{bmatrix} \\ \\\\ F=GE[i] F=[E00(n/2)−E00(n/2)W0(n/2)∗E00(n/2)W0(n/2)∗E00(n/2)]∗[G0(n/2)G1(n/2)]
到这一步,可以看到,我们已经成功将一个 n 阶的离散傅里叶变换降为了 n/2 阶,到这里就实现了O(n*logn)时间复杂度的快速傅里叶算法。
逆变换的和正变换的大同小异,就不在赘述了。
如果想要更简洁的形式,更深刻的理解离散傅里叶变换,可以进一步化简。
令
M=E00(n/2)∗G0(n/2)N=E00(n/2)∗G1(n/2)Z=W0(n/2)M=E_{00(n/2)}*G^{0(n/2)} \\\\ N=E_{00(n/2)}*G^{1(n/2)} \\\\ Z=W^{0(n/2)} \\\\ M=E00(n/2)∗G0(n/2)N=E00(n/2)∗G1(n/2)Z=W0(n/2)
则
F=[M+Z∗N−M+Z∗N]F = \begin{bmatrix} M+Z*N \\ -M+Z*N \\ \end{bmatrix} F=[M+Z∗N−M+Z∗N]
最后,上代码
public class FFT {/*** 傅里叶变换* @param x* @return*/public static Complex[] fft(Complex[] x){return fftTrans(x, true);}/*** 逆傅里叶变换* @param x* @return*/public static Complex[] ifft(Complex[] x) {int N = x.length;Complex[] y = fftTrans(x, false);for (int n = 0; n < N; n++) {y[n] = y[n].divides(N);}return y;}public static Complex[] fftTrans(Complex[] x, boolean dire) {int N = x.length;Complex[] y = new Complex[N];if (N == 1) {y[0] = x[0];return y;}Complex[] x0 = new Complex[N/2];for (int n = 0; n < N; n += 2) {x0[n/2] = x[n];}Complex[] X0 = fftTrans(x0, dire);Complex[] x1 = new Complex[N/2];for (int n = 1; n < N; n += 2) {x1[n/2] = x[n];}Complex[] X1 = fftTrans(x1, dire);for (int k = 0; k < N / 2; k++) {int ci = -1;if (!dire) {ci=-ci;}Complex wnk = getWnk(N, k, ci);Complex wnkX1 = wnk.multiply(X1[k]);y[k] = X0[k].plus(wnkX1);y[k+N/2] = X0[k].minus(wnkX1);}return y;}private static Complex getWnk(int N, int k, int n) {double T = 2 * Math.PI / N;double kth = T * k * n;Complex wk = new Complex(Math.cos(kth), Math.sin(kth));return wk;}}
相关文章:

通过矩阵从整体角度搞懂快速傅里叶变换原理
离散傅里叶变换公式 公式 f[k]∑n0N−1g[n]e−i(2π/N)kn,其中(0<n<N)f[k]\sum_{n0}^{N-1}g[n]e^{-i(2\pi/N)kn}, 其中(0<n<N) f[k]n0∑N−1g[n]e−i(2π/N)kn,其中(0<n<N) 逆变换公式 g[n]1N∑k0N−1f[k]ei(2π/N)kn,其中(0<k<N)g[n]\frac{1}{N}\…...

【C++从0到1】25、C++中嵌套使用循环
C从0到1全系列教程 1、实例代码 #include <iostream> // 包含头文件。 using namespace std; // 指定缺省的命名空间。int main() {// 超女分4个小组,每个小组有3名超女,在控制台显示每个超女的小组编号和组内编号。// 用一个循环…...
FastDFS与Nginx结合搭建文件服务器,并内网穿透实现公网访问
文章目录前言1. 本地搭建FastDFS文件系统1.1 环境安装1.2 安装libfastcommon1.3 安装FastDFS1.4 配置Tracker1.5 配置Storage1.6 测试上传下载1.7 与Nginx整合1.8 安装Nginx1.9 配置Nginx2. 局域网测试访问FastDFS3. 安装cpolar内网穿透4. 配置公网访问地址5. 固定公网地址5.1 …...
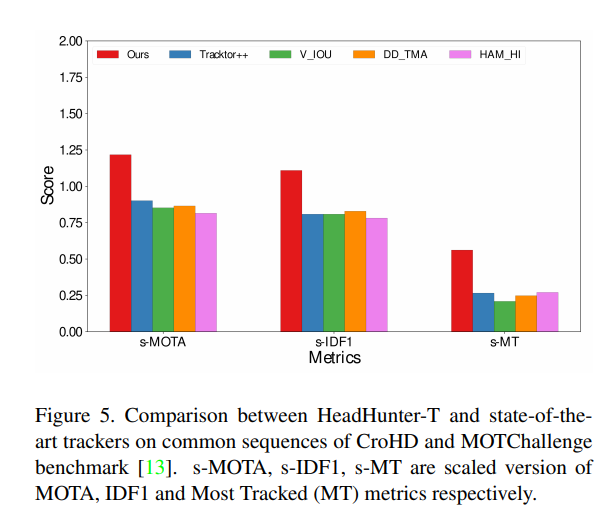
密集场景下的行人跟踪替代算法,头部跟踪算法 | CVPR 2021
一个不知名大学生,江湖人称菜狗 original author: Jacky LiEmail : 3435673055qq.com Time of completion:2023.4.8 Last edited: 2023.4.8 目录 摘要 主要内容 结果 这篇文章是CVPR 2021 的最新论文,文章的标题: 文章的主要内…...
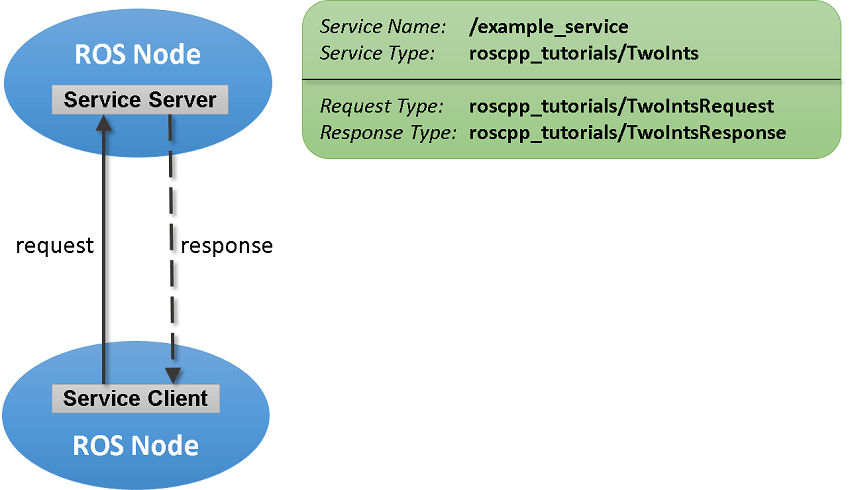
Matlab与ROS(1/2)---服务端和客户端数据通信(五)
0. 简介 在前几讲我们讲了Matlab中的Message以及Topic的相关知识。而ROS主要支持的通信机制还有服务这一类。服务通过允许请求以及响应的通信方式,来给整个系统完成更紧密的耦合。服务客户端向服务服务器发送请求消息并等待响应。服务器将使用请求中的数据构造响应…...

数字化转型的避坑指南:细说数字化转型十二大坑
随着信息技术的快速发展,数字化转型已经成为许多企业发展的必经之路。然而,数字化转型过程中也存在许多坑,如果不谨慎处理,就可能导致企业陷入困境。本文将细说数字化转型的十二大坑,并提供相应的避坑指南。 1、不了解…...

pt05Encapsulationinherit
Encapsulation &inherit 封装继承 封装 向类外提供必要的功能,隐藏实现的细节, 代码可读性更高优势:简化编程,使用者不必了解具体的实现细节,只需要调用对外提供的功能。私有成员:作用:无需向类外提供…...

面向对象编程(基础)9:封装性(encapsulation)
目录 9.1 为什么需要封装? 而“高内聚,低耦合”的体现之一: 9.2 何为封装性? 9.3 Java如何实现数据封装 9.4 封装性的体现 9.4.1 成员变量/属性私有化 实现步骤: 成员变量封装的好处: 9.4.2 私有化…...

fate-serving-server增加取数逻辑并源码编译
1.什么是fate-serving-server? FATE-Serving 是一个高性能、工业化的联邦学习模型服务系统,专为生产环境而设计,主要用于在线推理。 2.fate-serving-server源码编译 下载fate-serving-serving项目(GitHub - FederatedAI/FATE-Serving: A scalable, h…...
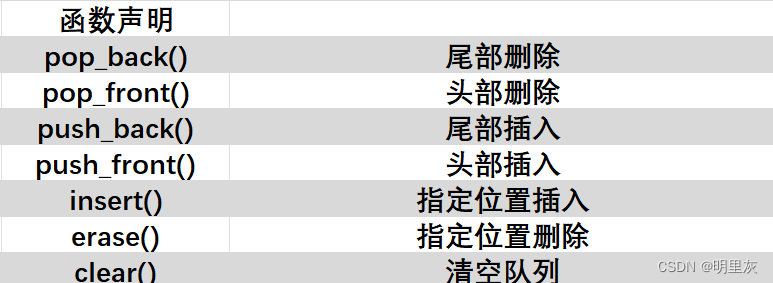
循环队列、双端队列 C和C++
队列 目录 概念 实现方式 顺序队列 循环队列 队列的数组实现 用循环链表实现队列 STL 之 queue 实现队列 STL 之 dequeue 实现双端队列 概念 队列是一种特殊的线性表,它只允许在表的前端(称为队头,front)进行删除操作…...
)
正则表达式(语法+例子)
文章目录一、介绍二、语法1、匹配字符2、表示数量的字符3、边界字符4、其他字符5、转义字符三、例子1、邮箱2、用逗号分隔的数字集合1,23、允许一位小数4、20yy-mm-dd日期格式5、手机号6、匹配html、xml标签一、介绍 正则表达式(Regular Expression)&am…...
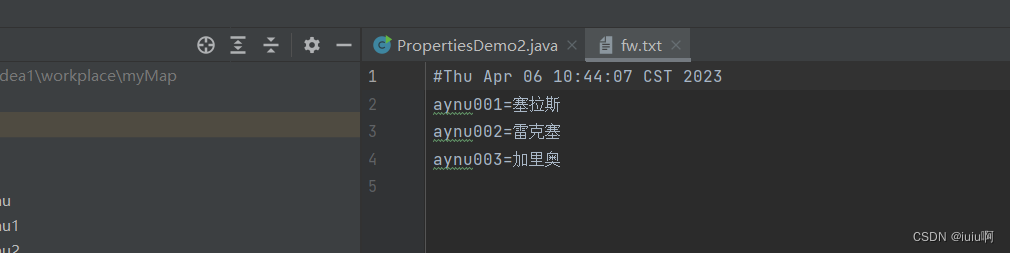
Properties和IO流集合的方法
方法名说明void load(InputStream inStream)从输入字节流读取属性列表(键和元素)void load(Reader reader)从输入字符流读取属性列表(键和元素对)void store(OutputStream out,String comments)将此属性列表(键和元素对…...
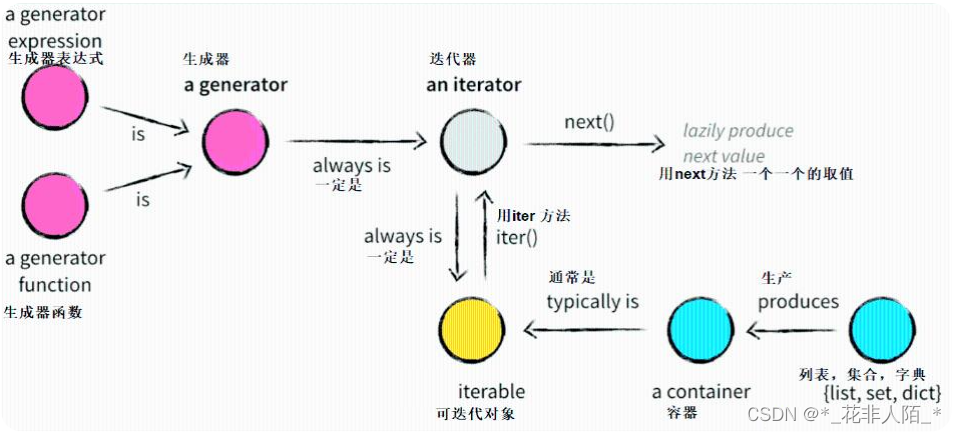
python 生成器、迭代器、动态新增属性及方法
目录 一、生成器 1、生成器定义 2、生成器存在的意义 3、创建生成器方式一(生成器表达式) 4. 创建生成器方式二(生成器函数) 1. 生成器函数 2. 生成器函数的工作原理 5. 总结 1. 什么是生成器 2. 生成器特点 二、迭代器…...

Java处理JSON
Java处理json有很多种方法,在这里总结一下。 1 Jackson Spring MVC 默认采用Jackson解析Json,出于最小依赖的考虑,也许Json解析第一选择就应该是Jackson。 1.1 引入的包 Jackson核心模块由三部分组成:jackson-core、jackson-a…...

58-Map和Set练习-LeetCode692前k个高频单词
题目 给定一个单词列表 words 和一个整数 k ,返回前 k 个出现次数最多的单词。 返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序 排序。 示例 1: 输入: words ["i", "love", …...
线程生命周期及五种状态
文章目录一、线程生命周期及五种状态1、New(初始化状态)2、Runnable(就绪状态)3、Running(运行状态)4、Blocked(阻塞状态)5、Terminated(终止状态)二、线程基本方法1、线程等待(wait)2、线程睡眠(sleep)3、…...

OBCP第八章 OB运维、监控与异常处理-灾难恢复
灾难恢复是指当数据库中的数据在被有意或无意破坏后复原数据库所需要执行的活动 回收站:回收站在原理上说就是一个数据字典表,放置用户删除的数据库对象信息。用户删除的东西被放入回收站后,其实仍然占据着物理空间,除非您手动进…...

亚马逊云科技Serverless Data:数字经济下的创新动能
Serverless时代已经到来!企业的技术架构,总是伴随着不断增长的数据与日趋复杂的业务持续演进。如何通过构建更易用的技术架构来聚焦在业务本身,而不必在底层基础设施的管理上投入过多的精力,是数据驱动型企业需要思考的重要议题。…...

【Ruby学习笔记】15.Ruby 异常
Ruby 异常 异常和执行总是被联系在一起。如果您打开一个不存在的文件,且没有恰当地处理这种情况,那么您的程序则被认为是低质量的。 如果异常发生,则程序停止。异常用于处理各种类型的错误,这些错误可能在程序执行期间发生&…...
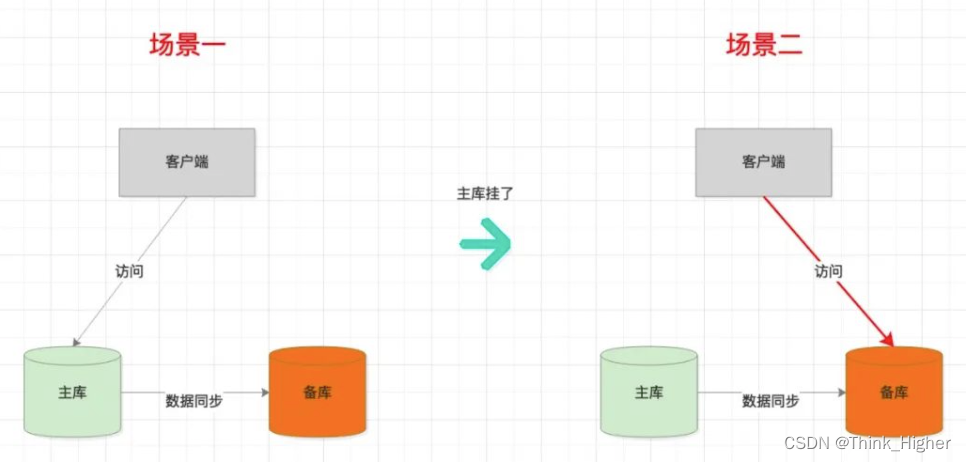
聊聊MySQL主从延迟
文章目录 MySQL 的高可用是如何实现的呢?二、什么是主备延迟?三、主备延迟常见原因1、备库机器配置差2、备库干私活3、大事务四、主库不可用,主备切换有哪些策略?1、可靠优先2、可用优先实验一实验二3、结论MySQL 的高可用是如何实现的呢? 高可用性(high availability,缩…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
