编译技术-词法理论
一、文法的种类
1.1 分类定义
Chomsky 文法定义:
- G=(V,Vt,P,Z)G = (V, V_t, P, Z)G=(V,Vt,P,Z)
- VVV:符号集合
- VtV_tVt:终结符号集合
- PPP :有穷规则集合
- ZZZ:是被符号,不能是终结符
关于不同文法的区别
| 类型 | 定义 | 接受 | 重点 |
|---|---|---|---|
| 0 型文法 | α::=β\alpha::=\betaα::=β | 图灵机 | 由字符串推导出另一个字符串,对于左部和右部都没有限制 |
| 1 型文法 | αUβ::=αuβ\alpha U \beta ::= \alpha u \betaαUβ::=αuβ | 线性界限的图灵机 | 要求左部必须有一个非终结符,而且一次只能改变一个非终结符,同时具有上下文敏感的特性 |
| 2 型文法 | U::=αU::= \alphaU::=α | 不确定的下推自动机 | 左部只能有一个非终结符(也就是上下文不敏感的),但是对于右部没有限制 |
| 3 型文法 | U::=Va,U::=aU::=Va, U:: = aU::=Va,U::=a | 有穷自动机 | 右部一定会推出终结符,而且右部很规则 |
在判断文法的时候,因为不同文法呈现包含关系,所以应当按照 3−>2−>1−>03 -> 2 -> 1 -> 03−>2−>1−>0 的顺序去判断。
当一个文法的右部呈现正则形式的时候,那么为 3 型文法,否则判断左部,如果左部都是一个非终结符,那么就是 2 型。然后判断是否每条规则只改变一个非终结符,不是则为 0 型。
1.2 三型文法直观感受
因为只有两种推导形式,所以其语法树会长得很“偏瘫”,比如说对于左线性文法,就是长成这个样子的:

正是因为这种“偏瘫”的性质,才使得有限状态机成为接受三型文法的工具,可以一个个字符的读入,而且没有“回溯”过程。其推导的过程就好像我们平时书写一样,成一个线性的趋势。
1.3 上下文无关特性
我们说大部分高级程序设计语言都是二型文法,具有上下文无关的特性,但是其实对于复杂特性的语言,比如说 CPP(对,又是它),他是具有上下文敏感的特性的,比如说
a<b<c>> d
可以被理解成一个
vector<vector<int>> matrix;
也可以被理解成位运算
int x = 4 < 3 < 2 >> 1
所以在“不引入符号表”(可以看做符号表就是记录上下文信息的工具)的前提下,是没有办法进行语法分析的,所以 CPP 会进行一种“试错式”的语法分析,就好像我们的错误处理一样。
递归下降法更适合分析二型文法(也不是完全都可以分析出来),而不适合分析一型文法,所以在实验课中,一旦引入错误处理(也就是相当于引入了一些一型文法)就会导致语法分析没有办法是朴素的递归下降,而是必须进行尝试性回溯,这是递归下降的局限性。
有一个观点很有意思,就是词法分析,语法分析,语义分析其实完成的是同一个任务的不同部分,所以我们在设计的时候,可以考虑将总任务分给这三个部分,当一个部分被设计的简单的时候,另一个部分就会被设计的复杂,比如说 python 如果按照普通理解,其实是一型文法,因为缩进的原因,语法变得上下文敏感了,但是实际上是二型文法,这是因为缩进在词法分析的时候被处理成了“缩进增”和“缩进减”,这与“左大括号”和“右大括号”是等价的。另一个例子,肯定程序本身是上下文相关的(又不是计算器),那么相当于符号表这类语义分析中上下文敏感的实现,代替了复杂的语法分析,使得语法分析可以很简单。
另外文法不仅和表达能力相关,它同时也与计算能力相关,所以只有 0 型文法具有图灵机的全部能力,严格讲高级语言并不能够发挥出其全部实力。据说 lisp 是基于 0 型文法的。
1.4 文法的等价性
文法的等价性指的是如果两个文法描述的语言是相等的,那么就称这个两个文法是等价的,也就是说,这并不涉及文法的本身性质,一个三型文法可以与一个一型文法等价,并无大碍。
二、正则转换
2.1 等价转换框架

如图所示,图上的这五种东西是等价的,并且是可以相互转化的(虽然有一些是没有意义的),下面将分别介绍。
2.2 正则文法与 DFA 转换
正则文法又称为 3 型文法。正则文法有两种,左线性和右线性,分别长这样
- 左线性:A ::= Bt
- 右线性:A ::= tB
之前觉得正则文法就已经可以描述很多东西了(我以为 SysY 是可以用正则文法表示的),但是其实正则文法连基本的表达式都没有办法表达。所以正则一般都用于词法分析,语法分析其就不适用了。
首先讨论正则文法转换为 DFA
对于左线性文法,有如下方法
- 对于 A::=BtA ::= BtA::=Bt ,有 δ(B,t)=A\delta(B, t) = Aδ(B,t)=A
- 对于 A::=tA ::= tA::=t,有 δ(S,t)=A\delta(S, t) = Aδ(S,t)=A ,其中 SSS 为状态机的起始状态
- 状态机只有一个终止状态 ZZZ ,同时 ZZZ 是正则文法的起始符号(识别符号)。
举个例子

不可否认,左线性有些不自然,因为明明是 A→BA \rightarrow BA→B 这种规则,但是最后的边却是 B→AB \rightarrow AB→A ,恰恰反过来,但是并非毫无道理,相反,当前状态代表着已经规约的非终结符,是一种自底向下的过程,进行最左规约,如下所示

对于右线性文法:
- 对于 A::=tBA ::= tBA::=tB ,有 δ(A,t)=B\delta(A, t) = Bδ(A,t)=B
- 对于 A::=tA ::= tA::=t,有 δ(A,t)=Z\delta(A, t) = Zδ(A,t)=Z ,其中 ZZZ 为状态机的终止状态
- 状态机只有一个起始状态 SSS ,同时 SSS 是正则文法的起始符号(识别符号)。
这就很好理解,这是一个自顶向下的过程,当前状态是要解析的非终结符。这么看,正则文法真的有很多很好的性质,他们的 FIRSTFIRSTFIRST 和 FOLLOWFOLLOWFOLLOW 都是直白的,这就导致其对于语法规则的选择很简单。
对于 DFA 转换成正则文法,一般转换为左线性文法,并不可以直接看成逆过程,有如下规则
- 对转换函数 δ(A,t)=B\delta(A, t) = Bδ(A,t)=B ,可写成一个产生式:A::=tBA ::= tBA::=tB
- 对于终止状态,可写成一个产生式:Z::=εZ::=\varepsilonZ::=ε
- DFA 的初态对应于文法的开始符号(识别符号)。
如下示例:

2.3 正则文法与正则表达式
比较简单,需要注意的是,当正则文法向正则表达式转换的时候,应用的不只是转换法则,还有正则表达式的运算。
由正则文法转正则表达式:

由正则表达式转正则文法:

2.4 正则表达式与 NFA
第一条规则描述的是很“显然”的事情,他说的是,对于一个正则表达式,它天然拥有“开始”和“终止”两个状态,他们中间会有一条边或者一堆状态和一堆边。

在这里其实可以反思一个事情,就是在 DFA 或者在 NFA 中,绝对不会有从一个状态中出现两条相同的边,也就是

这是显然的,因为这样在 AAA 状态输入 xxx ,就并不知道是应当转移到 BBB 还是应当转移到 CCC 。但是对于 ϵ\epsilonϵ 却没有这个约束,如下所示

下面的规则都是这种现象的体现,他们会给 NFA 引入大量的 ϵ\epsilonϵ 。这显然是不利于 NFA 到 DFA 的化简的(后面的例题也有说明),为了规避这种现象,我们考虑将一些的 ϵ\epsilonϵ 化简掉。在化简中,这样形式的正则表达式可以十分有用
X=aYbX = aYb X=aYb
其中 YYY 可以是任何正则表达式,a,ba, ba,b 是终止符,这个表达式意味着,XXX 一定是由 aaa 开头,由 bbb 结尾,这个是一个很好的性质,我们可以将开头的 ϵ\epsilonϵ 和结尾的 ϵ\epsilonϵ 可以分别被替换成 a,ba, ba,b 。这种替换只要不会导致 NFA 的定义被违反(也就是上面提到的情况),那么就是可行的。


反之:

2.5 NFA 转 DFA
首先是确定 I(S)I(S)I(S) 这是一种 I−εI-\varepsilonI−ε 闭包,说的是开始状态和可以通过 ε\varepsilonε 到达的状态组成的集合。
然后需要通过边访问,比如说 Ia(S)I_a(S)Ia(S) ,表示的是通过 aaa 这条边, I(S)I(S)I(S) 可以到达的状态的集合,而且这个集合中还有通过 ε\varepsilonε 到达的状态,换句话说,也是闭包。
然后就这么周而复始的运动即可。
实际操作的时候是真的难,首先是这种题一般是给出正则表达式,然后求最小 DFA。那么如果不幸构造出一个极其复杂的 NFA,那就真的完蛋了,比如说下面的例子,如果按照规则构造的话,是这样的
a((a∣b)∗∣ab∗a)∗b\tt{a((a|b)*|ab*a)*b } a((a∣b)∗∣ab∗a)∗b
正常构造是 7 个状态

然后就会陷入无限的求解闭包的过程(甚至 DFA 的状态比 NFA 还多)中,所以应当用前面介绍的方法,先手动化简成这样

具体的过程是这样的,考虑题目
a((a∣b)∗∣ab∗a)∗b\tt{a((a|b)*|ab*a)*b } a((a∣b)∗∣ab∗a)∗b
可以知道,大概会翻译成这样

然后进行一个显然的化简

然后观察子正则表达式,发现 ab∗a\tt{ab*a}ab∗a 发现他是以 aaa 开头结尾的,所以可以进行化简
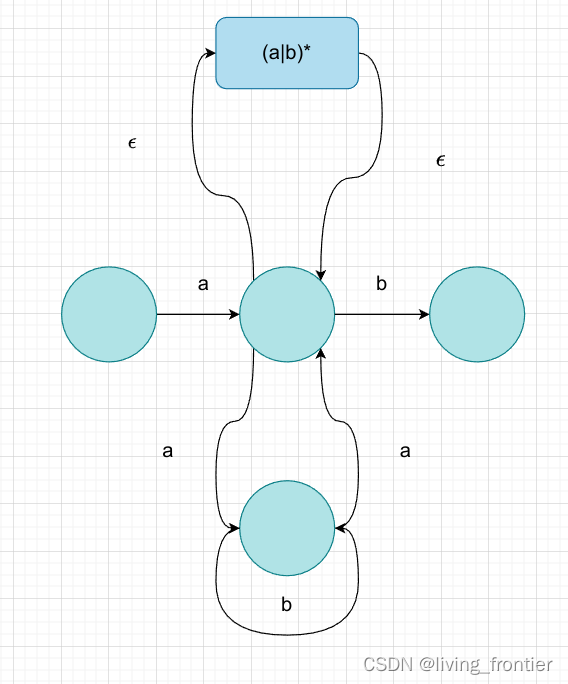
其核心在于不能让一个状态有两个同为 ε\varepsilonε 的出边或者入边,显然是可以化简的,而且这种太难搞了。
然后进行化简的时候,可以考虑先对于每个状态求一遍闭包,这样对于多个状态的合并,就不需要多次重复计算了,如下所示
| 状态 | a | b |
|---|---|---|
| 1 | 2, 3 | |
| 2 | 3, 4 | 2, 3, 5 |
| 3 | 2, 3, 4 | 3, 5 |
| 4 | 2, 3 | 4 |
| 5 |
这里一定要小心谨慎,因为一不小心就错了。
然后就可以进行查表求解过程了,因为 DFA 的状态也需要标识,所以建议用英文字母与原来 NFA 的阿拉伯数字区分
| DFA | NFA | a | b |
|---|---|---|---|
| A | 1 | 2, 3 | |
| B | 2, 3 | 2, 3, 4 | 2, 3, 5 |
| C | 2, 3, 4 | 2, 3, 4 | 2, 3, 4, 5 |
| D | 2, 3, 5 | 2, 3, 4 | 2, 3, 5 |
| E | 2, 3, 4, 5 | 2, 3, 4 | 2, 3, 4, 5 |
2.6 最小化 DFA
采用分割法进行计算,不过必须要承认,这个方法实际上的如果按照严谨的计算,那么运算量是极其复杂的,是没有办法很容易的得出答案,在得出答案的过程中,还需要不断的依靠直觉,而且似乎具有某些不动点算法的性质。
最小化 DFA 干的事情就是将 DFA 中“等价”的状态合并到一起,主要考虑两个条件:
- 一致性条件:状态 sss 和状态 ttt 必须同时为接受状态或者非接受状态。这个很显然,也很好判断。
- 蔓延性条件:对于所有的输入符号,状态 sss 和状态 ttt 必须转换到等价状态里。这个就是很符合直观认知的,但是很难应用,因为等价状态是一个变化的东西。
在教材上,只是用例子演示了一下,并没有完整的算法。我凑活写了一个:
- 首先利用一致性条件,将状态划分为两个集合。
- “认为“此时每个集合里的每个状态都是等价的。
- 基于第二点,遍历集合中的每个状态,利用蔓延性条件检验是否真的与该状态所在集合的其他状态等价,当出现不等价情况,分割集合,回到第二点。如果所有状态均检查完毕,则算法结束。
以一道题举例:这是状态转移表
| a | b | |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 7 | 3 |
| 3 | 1 | 5 |
| 4 | 4 | 6 |
| 5 | 7 | 3 |
| 6 | 4 | 1 |
| 7 | 4 | 2 |
其中接受状态是 {5,6,7}\{5, 6, 7\}{5,6,7} 。
原题在求解的时候,在这张表的右侧拓展了一列,用于分区,但是这是不严谨的,因为我们并不保证等价状态一定在表上挨在一起。所以考虑手写集合。
首先根据一致性条件划分出两个集合
{1,2,3,4},{5,6,7}\{1, 2, 3, 4\}, \{5, 6, 7\}{1,2,3,4},{5,6,7}
然后遍历 1,发现 2 和 1 等价,但是和 3 不等价,所以分割出 1,2
{1,2},{3,4},{5,6,7}\{1, 2\}, \{3, 4\}, \{5, 6, 7\}{1,2},{3,4},{5,6,7}
此时遍历 1,2 没有问题,遍历 3,发现和 4 不等价,所以分割数 3
{1,2},{3},{4},{5,6,7}\{1, 2\}, \{3\}, \{4\}, \{5, 6, 7\}{1,2},{3},{4},{5,6,7}
遍历 1,2,3,4 没有问题,遍历 5,发现与 6 不等价,所以分割 5
{1,2},{3},{4},{5},{6,7}\{1, 2\}, \{3\}, \{4\}, \{5\}, \{6, 7\}{1,2},{3},{4},{5},{6,7}
检查完毕,算法结束。
相关文章:

编译技术-词法理论
一、文法的种类 1.1 分类定义 Chomsky 文法定义: G(V,Vt,P,Z)G (V, V_t, P, Z)G(V,Vt,P,Z)VVV:符号集合VtV_tVt:终结符号集合PPP :有穷规则集合ZZZ:是被符号,不能是终结符 关于不同文法的区别 类型…...

【20】核心易中期刊推荐——计算机科学电子通信(EI索引)
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

Vue 3.0 风格指南 2
#元素 attribute 的顺序推荐 元素 (包括组件) 的 attribute 应该有统一的顺序。 这是我们为组件选项推荐的默认顺序。它们被划分为几大类,所以你也能知道新添加的自定义 attribute 和指令应该放到哪里。 定义 (提供组件的选项) is列表渲染 (创建多个变化的相同元素…...

ChatGPT遭多国调查,OpenAI凌晨就安全问题发文,GPT-5要暂缓?
最近,意大利宣布禁用 ChatGPT,因为 OpenAI 违反了意大利相关的隐私规则和数据保护法,出现了用户数据丢失情况,而且未向用户告知。 消息出来后,德国、法国、爱尔兰、西班牙等国的监管部门都表示正在密切关注 ChatGPT 的…...

网络安全书籍推荐
网络安全书籍推荐 ,对于网络安全的初学者来说,能很好的选择教材,鉴于只有英文版,我尝试翻译成中文以供参考,初次翻译,翻译的不好请见谅。 标题注解技术等级The Art of Software Security Assessment软件安…...
)
【独家】华为OD机试 - 狼羊过河 or 羊、狼、农夫过河(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:狼羊过河 or 羊、狼、农夫过河…...

东八区的 springboot 如何配置序列化
东八区的 springboot 🚞使用SpringBoot默认配置自定义配置类自定义 ObjectMapper自定义序列化器总结我接受它的苦,它的灰暗,它的刺,因为总会过去,我的花会开,生活也会慢慢拥抱我 使用SpringBoot默认配置 S…...

论文阅读_LLaMA
论文信息 number headings: auto, first-level 2, max 4, _.1.1 name_en: LLaMA: Open and Efficient Foundation Language Models name_ch: LLaMA: 开放高效的基础语言模型 paper_addr: https://arxiv.org/abs/2302.13971 doi: https://doi.org/10.48550/arXiv.2302.13971 da…...
腾讯空降测试工程师,绩效次次拿S,真是砂纸擦屁股,给我露了一手啊
上周我们公司的绩效面谈全部结束了,每年到这个时间点就是打绩效的时候了,对于职场打工人来说绩效绝对是最重要的事情之一,原因也很简单:奖金、晋升、涨薪都和它有关系。 比如下面这个美团员工在脉脉上的自曝就很凄凉࿱…...
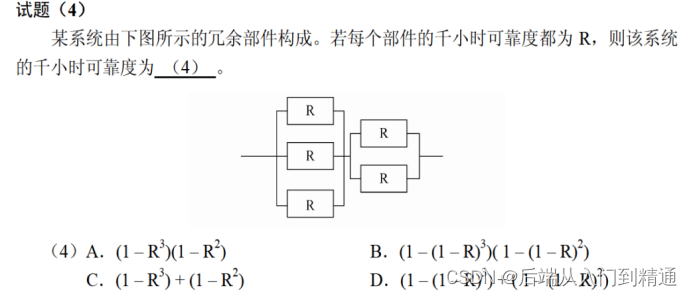
真题详解(计算机总线)-软件设计(四十五)
真题详解(二维数组)-软件设计(四十四)https://blog.csdn.net/ke1ying/article/details/130023062 1、2016年下半年 解析: A选项,当B中的两个结束都到达,会转到C2,因为C2没有事件&a…...
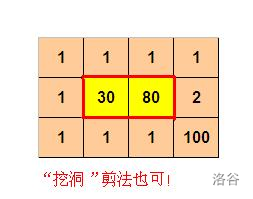
剪格子
[蓝桥杯 2013 省 A] 剪格子 题目描述 如图 111 所示,333\times 333 的格子中填写了一些整数。 我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 606060。 本题的要求就是请你编程判定:对给定的 mnm\times nmn 的格…...

【Nowcoder-BC146.添加逗号 -OR63.删除公共字符】
Nowcoder-BC146.-OR63.Nowcoder-BC146.添加逗号Nowcoder-OR63.删除公共字符Nowcoder-BC146.添加逗号 题目:对于一个较大的整数 N(1<N<2,000,000,000) 比如 980364535,我们常常需要一位一位数这个数字是几位数,但是如果在这个数字每三位…...

能自动摊铺施工的公路滑模机多少钱一台
滑模机是能在公路施工现场进现场自动摊铺作业的设备,让路缘石经过设备制作一次性完成施工工序,整体成型一次完成。这样的使用流程整体包含了几个大的关键步骤,分别是测量后放置标示线-设备进场就位-原材料运输和供应-滑模机摊铺作业-后续伸缩…...

ChatGPT热潮下,因生成式AI失业的人出现,我成了第一批失业的人
近几个月来,越来越多的知名人士预计,年内大热的ChatGPT有望掀起一场新的工业革命。而纵观历史,历次工业革命往往会深远改变当时的社会结构——从机械织布机到内燃机再到第一台计算机,新技术的出现总是会引起人们对于被机器取代的恐…...

TypeScript01-基础知识
基础类型 boolean 类型 let isDone: boolean false; // ES5:var isDone false;number 类型 let count: number 10; // ES5:var count 10;string 类型 let name: string "semliker"; // ES5:var name semlinker;Symbol 类…...

【Redis学习】Redis安装配置
Linux 安装环境必须先具备gcc编译环境 版本选择 查看自己redis版本的命令 安全Bug按照官网提示,升级成为6.0.8及以上 目前建议都需要升级到6.0.8版本以上 本次我们用Redis7.0 Redis7安装步骤 下载获得redis-7.0.0.tar.gz后将它放入Linux目录/opt /opt目录下解…...

leetcode160:相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 图示两个链表在节点 c1 开始相交: 题目数据 保证 整个链式结构中不存在环。 注意,函数返回结果后…...

基于Prometheus的jvm监控指标详解
使用Prometheus 监控Springboot应用参考 Prometheus Operator实战—— Prometheus、Alertmanager、Grafana 监控Springboot服务 下面来看看jvm的监控指标 # HELP jvm_gc_collection_seconds Time spent in a given JVM garbage collector in seconds. # TYPE jvm_gc_collection…...
C程序设计语言基础
机器语言与高级语言 计算机硬件只能够识别电平信号,正电平或负电平,计算机的的各种按钮触发各种电平与计算机交互。随着随着操作系统的发展,人们用1,0分别表示正电平和负电平,并由0,1所组成的一系列指令指…...

构建同一局域网下文件共享网页
首先,我会将这个内容分成以下步骤: 目录 1. 安装必要的软件和工具 2. 搭建本地服务器 3. 编写账号系统和登录页面 4. 实现多人登录 5. 实现文件上传和共享功能 以下是每个步骤的详细说明和代码示例。 1. 安装必要的软件和工具 为了完成这个项目&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
