【每日一题Day166】LC1053交换一次的先前排列 | 贪心
交换一次的先前排列【LC1053】
给你一个正整数数组
arr(可能存在重复的元素),请你返回可在 一次交换(交换两数字arr[i]和arr[j]的位置)后得到的、按字典序排列小于arr的最大排列。如果无法这么操作,就请返回原数组。
虽然写出来了,但是花了55分钟…
还是有思路但是思路不清晰,然后直接敲代码,改来改去,老毛病了
笔试绝对ggg
看了别人的贪心,感觉自己笨笨的
-
思路:贪心
假设交换的左边元素为arr[i]arr[i]arr[i],右边的元素为arr[j]arr[j]arr[j]
-
怎样交换一次可以使字典序减小?
交换元素arr[i]>arr[j]arr[i]>arr[j]arr[i]>arr[j]时,可以使字典序较小,所以数组必须是非递增的
-
如何使字典序小于原数组的情况下最大?【贪心】
保留前面高位部分的数组,尽可能交换低位部分的数组,即尽可能最小化jjj的同时,最大化iii
枚举每个右端点,此时的右端点rrr必须小于等于nums[j]nums[j]nums[j],找到在[i,r−1][i,r-1][i,r−1]范围内,从右往左第一个大于其的左端点进行交换
- 如果arr[r]>arr[j]arr[r] > arr[j]arr[r]>arr[j], 那么从右往左第一个大于arr[r]arr[r]arr[r]的左端点一定在i的左边包括i,那么我们无法获得比目前的排列更大的排列
- 如果arr[r]==arr[j]arr[r] == arr[j]arr[r]==arr[j], 那么从右往左第一个大于arr[r]arr[r]arr[r]的左端点还是为iii,只需要修改右端点
- 如果arr[r]<arr[j]arr[r] < arr[j]arr[r]<arr[j], 那么lll需要在[i+1,r−1][i+1,r-1][i+1,r−1]的范围内才可能是字典序增大
-
-
实现
class Solution {public int[] prevPermOpt1(int[] arr) {int n = arr.length;int l = 0;// 升序数组本身就是最小排列while (l < n - 1 && arr[l] <= arr[l + 1]){l++;}if (l == n - 1) return arr; // 升序数组// 非升序数组 枚举每个右端点 找到从右往左第一个大于其的左端点进行交换// 之后交换的右端点必须小于等于arr[j],并且左端点l必须大于i才能使交换结果变小// 如果arr[r] > arr[j], 那么从右往左第一个大于arr[r]的左端点一定在i的左边包括i,那么我们无法获得比目前的排列更大的排列// 如果arr[r] == arr[j], 那么从右往左第一个大于arr[r]的左端点还是为i,只需要修改右端点// 如果arr[r] < arr[j], 那么l需要在[i+1,r-1]的范围内才可能是字典序增大int i = -1, j = -1;// 记录最终的交换结果for (int r = n - 1; r > i; r--){if (j != -1 && arr[r] > arr[j]) continue;if (j != -1 && arr[r] == arr[j]) {j = r;continue;}for (l = r - 1; l >= (i != -1 ? i + 1 : 0); l--){if (arr[l] > arr[r]){i = l;j = r;break;}}}// 交换int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;return arr;} }- 复杂度
- 时间复杂度:O(n2)O(n^2)O(n2)
- 空间复杂度:O(1)O(1)O(1)
- 复杂度
-
别人的贪心
我们先从右到左遍历数组,找到第一个满足 arr[i−1]>arr[i]arr[i−1]>arr[i]arr[i−1]>arr[i]的下标 iii,此时 arr[i−1]arr[i−1]arr[i−1]就是我们要交换的数字,我们再从右到左遍历数组,找到第一个满足 arr[j]<arr[i−1]arr[j]<arr[i−1]arr[j]<arr[i−1] 且 arr[j]≠arr[j−1]arr[j] \neq arr[j - 1]arr[j]=arr[j−1] 的下标j,此时我们交换 arr[i−1]arr[i−1]arr[i−1] 和 arr[j]arr[j]arr[j] 后返回即可。
class Solution {public int[] prevPermOpt1(int[] arr) {int n = arr.length;for (int i = n - 1; i > 0; --i) {if (arr[i - 1] > arr[i]) {for (int j = n - 1; j > i - 1; --j) {if (arr[j] < arr[i - 1] && arr[j] != arr[j - 1]) {int t = arr[i - 1];arr[i - 1] = arr[j];arr[j] = t;return arr;}}}}return arr;}
}作者:ylb
链接:https://leetcode.cn/problems/previous-permutation-with-one-swap/solutions/2205403/python3javacgotypescript-yi-ti-yi-jie-ta-pxxt/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 复杂度
- 时间复杂度:O(n)O(n)O(n)
- 空间复杂度:O(1)O(1)O(1)
相关文章:

【每日一题Day166】LC1053交换一次的先前排列 | 贪心
交换一次的先前排列【LC1053】 给你一个正整数数组 arr(可能存在重复的元素),请你返回可在 一次交换(交换两数字 arr[i] 和 arr[j] 的位置)后得到的、按字典序排列小于 arr 的最大排列。 如果无法这么操作,…...

Canal增量数据订阅和消费——原理详解
文章目录 简介工作原理MySQL主备复制原理canal 工作原理Canal-HA机制应用场景同步缓存 Redis /全文搜索 ES下发任务数据异构简介 canal 翻译为管道,主要用途是基于 MySQL 数据库的增量日志 Binlog 解析,提供增量数据订阅和消费。 早期阿里巴巴因为杭州和美国双机房部署,存…...

为什么要使用线程池
Java线程的创建非常昂贵,需要JVM和OS(操作系统)配合完成大量的工作: (1)必须为线程堆栈分配和初始化大量内存块,其中包含至少1MB的栈内存。 (2)需要进行系统调用,以便在OS(操作系统)…...

在云服务部署前后端以及上传数据库
1.上传数据库(sql文件) 首先建立一个目录,用于存放要部署的sql文件,然后在此目录中进入mysql 进入后建立一个数据库,create database 数据库名 完成后,通过select * from 表名可以查到数据说明导入成功。 2.部署Maven后端 将Ma…...

Onedrive for Business迁移方案 | 分享一
文章目录 前言 一、Onedrive for Business迁移方案应用范围? 1.准备目标平台 2.导出源平台数据 <...

pt01数据类型、语句选择
python01 pycharm常用快捷键 (1) 移动到本行开头:home键 (2) 移动到本行末尾:end键盘 (3) 注释代码:ctrl / (4) 复制行:ctrl d #光标放行上 (5) 删除行:shift delete (6) 选择列:shift alt 鼠标左键…...
ChatGPT 存在很大的隐私问题
当 OpenAI 发布时 2020 年 7 月的 GPT-3,它提供了用于训练大型语言模型的数据的一瞥。 根据一篇技术论文,从网络、帖子、书籍等中收集的数百万页被用于创建生成文本系统。 在此数据中收集的是您在网上分享的一些关于您自己的个人信息,这些数据现在让 O…...
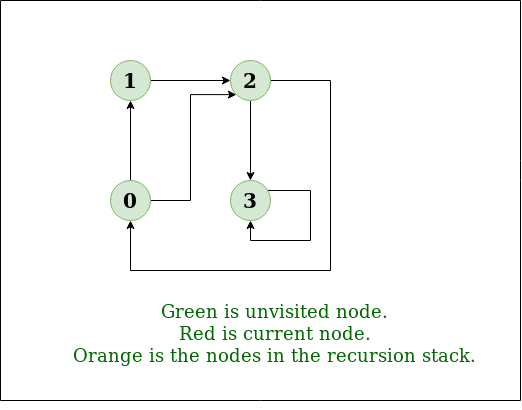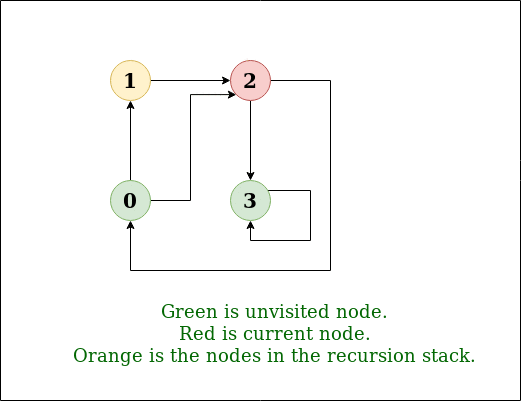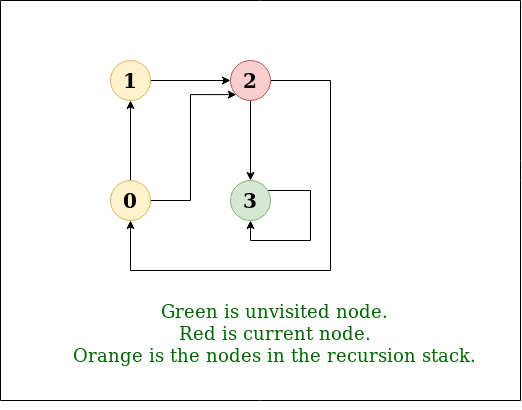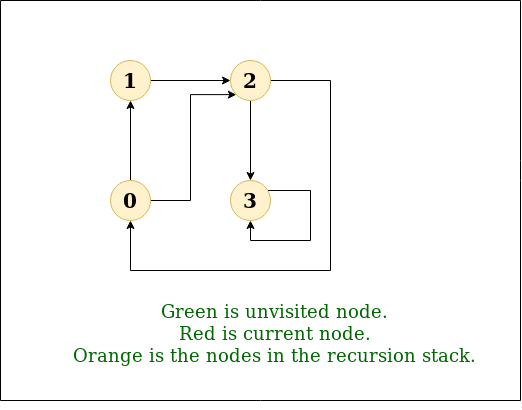
图的迭代深度优先遍历
图的深度优先遍历(或搜索)类似于树的深度优先遍历(DFS)。这里唯一的问题是,与树不同,图可能包含循环,因此一个节点可能会被访问两次。为避免多次处理一个节点,请使用布尔访问数组。 例子: 输入: n = 4, e = 6 0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, …...

华为OD机试-开放日活动-2022Q4 A卷-Py/Java/JS
某部门开展Family Day开放日活动,其中有个从桶里取球的游戏,游戏规则如下:有N个容量一样的小桶等距排开,且每个小桶都默认装了数量不等的小球, 每个小桶装的小球数量记录在数组 bucketBallNums 中,游戏开始时,要求所有…...

两亲性聚合物:Lauric acid PEG Maleimide,Mal-PEG-Lauric acid,月桂酸PEG马来酰亚胺,试剂知识分享
Lauric acid PEG Maleimide,Lauric acid PEG Mal| 月桂酸PEG马来酰亚胺 | CAS:N/A | 端基取代率:95%一、试剂参数信息: 外观(Appearance):灰白色/白色固体或粘性液体取决于分子量 溶解性&am…...

FB使用入口点函数例子
一、DLL的入口点 1.1 VFB的自带DLL模式入口 FB是把代码转成C(GCC编译)或者汇编(GAS编译)后编译的,本身就有一个main函数,所以在程序里其实不需要入口点,直接写就可以顺序执行,而有的…...
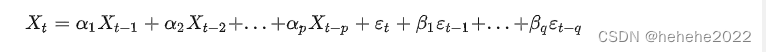
学习周报4/9
文章目录前言文献阅读摘要简介方法结论时间序列预测总结前言 本周阅读文献《Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: A case study of three mountainous areas on the Tibetan Plateau》,文章主要基于…...

49天精通Java,第14天,Java泛型方法的定义和使用
目录一、基本介绍1、Java泛型的基本语法格式为:2、在使用泛型时,还需要注意以下几点:二、泛型的优点1、类型安全2、消除强制类型转换3、更高的效率4、潜在的性能收益三、常见泛型字母含义四、使用泛型时的注意事项五、泛型的使用1、泛型类2、…...

20230402英语学习
reasonable adj.合理的;通情达理的;明智的,理智的 abstract adj.抽象的,理论的 reflection n.反射; 映像, 倒影; 反映; 表达, 抒发; (长相等)酷似的人; 惟妙惟肖的事物; 深思; 考虑 instruction n.教授; 教导, 指导; 指示, 命令…...
SpringCloud)
Java知识复习(十七)SpringCloud
1、什么是微服务架构 微服务架构就是将单体的应用程序分成多个应用程序,这多个应用程序就成为微服务,每个微服务运行在自己的进程中,并使用轻量级的机制通信这些服务围绕业务能力来划分,并通过自动化部署机制来独立部署。这些服务…...
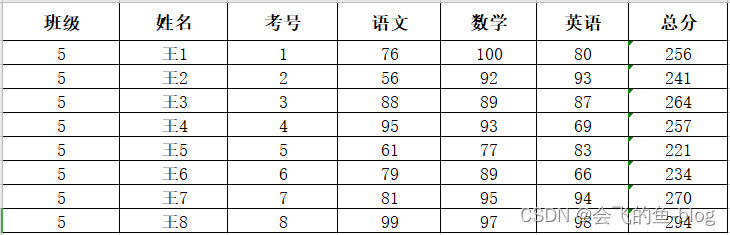
MySQL 数据库操作
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、关系模型二、数据库的操作 创建数据库查看数据库选择数据库删除数据库三、MySQL 数据库命名规范总结一、关系模型 关系数据库是建立在关系模型上的。而关系模…...

Cesium更换地球背景
设置背景图片 #cesiumContainer {width: 100%;height: 100%;background-image: url("/assets/image/背景.png"); }设置渲染, 用来去掉地球表面的大气效果的黑圈问题 this.viewer new Cesium.Viewer("cesiumContainer", {......// 设置渲染orderIndepe…...

测试人员的瓶颈期
测试人员的瓶颈期 做测试久了,会在所难免地碰到职业瓶颈期,这很正常,从事任何职业的工作人员都会遇到,关键是要看你如何去克服它。对优秀的软件测试人员来讲,除了要具备全面的技能、丰富的经验、良好的心理素质&#x…...

HTML5 <form> 标签
HTML5 <form> 标签 实例 带有两个输入字段和一个提交按钮的 HTML 表单: <form action"demo_form.php" method"get">First name: <input type"text" name"fname"><br>Last name: <input type&qu…...
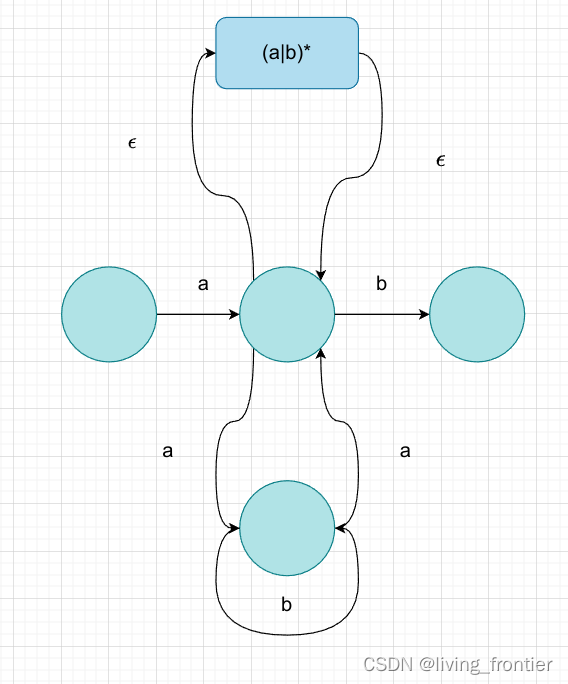
编译技术-词法理论
一、文法的种类 1.1 分类定义 Chomsky 文法定义: G(V,Vt,P,Z)G (V, V_t, P, Z)G(V,Vt,P,Z)VVV:符号集合VtV_tVt:终结符号集合PPP :有穷规则集合ZZZ:是被符号,不能是终结符 关于不同文法的区别 类型…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
