【机器学习】P10 从头到尾实现一个线性回归案例
这里写自定义目录标题
- (1)导入数据
- (2)画出城市人口与利润图
- (3)计算损失值
- (4)计算梯度下降
- (5)开始训练
- (6)画出训练好的模型
- (7)做出预测
- (8)完整代码
(1)导入数据
问题引入:假设你是老板,要考虑在不同的城市开一家新店;
x_train 是不同城市的人口数量
y_train 是那个城市一家餐馆的利润
import math
import copy
import numpy as npx_train = np.array([6.1101, 5.5277, 8.5186, 7.0032, 5.8598, 8.3829, 7.4764, 8.5781, 6.4862, 5.0546, 5.7107, 14.164, 5.734, 8.4084, 5.6407, 5.3794, 6.3654, 5.1301, 6.4296, 7.0708, 6.1891, 20.27, 5.4901, 6.3261, 5.5649, 18.945, 12.828, 10.957, 13.176, 22.203, 5.2524, 6.5894, 9.2482, 5.8918, 8.2111, 7.9334, 8.0959, 5.6063, 12.836, 6.3534, 5.4069, 6.8825, 11.708, 5.7737, 7.8247, 7.0931, 5.0702, 5.8014, 11.7, 5.5416, 7.5402, 5.3077, 7.4239, 7.6031, 6.3328, 6.3589, 6.2742, 5.6397, 9.3102, 9.4536, 8.8254, 5.1793, 21.279, 14.908, 18.959, 7.2182, 8.2951, 10.236, 5.4994, 20.341, 10.136, 7.3345, 6.0062, 7.2259, 5.0269, 6.5479, 7.5386, 5.0365, 10.274, 5.1077, 5.7292, 5.1884, 6.3557, 9.7687, 6.5159, 8.5172, 9.1802, 6.002, 5.5204, 5.0594, 5.7077, 7.6366, 5.8707, 5.3054, 8.2934, 13.394, 5.4369])
y_train = np.array([17.592, 9.1302, 13.662, 11.854, 6.8233, 11.886, 4.3483, 12., 6.5987, 3.8166, 3.2522, 15.505, 3.1551, 7.2258, 0.71618, 3.5129, 5.3048, 0.56077, 3.6518, 5.3893, 3.1386, 21.767, 4.263, 5.1875, 3.0825, 22.638, 13.501, 7.0467, 14.692, 24.147, -1.22, 5.9966, 12.134, 1.8495, 6.5426, 4.5623, 4.1164, 3.3928, 10.117, 5.4974, 0.55657, 3.9115, 5.3854, 2.4406, 6.7318, 1.0463, 5.1337, 1.844, 8.0043, 1.0179, 6.7504, 1.8396, 4.2885, 4.9981, 1.4233, -1.4211, 2.4756, 4.6042, 3.9624, 5.4141, 5.1694, -0.74279, 17.929, 12.054, 17.054, 4.8852, 5.7442, 7.7754, 1.0173, 20.992, 6.6799, 4.0259, 1.2784, 3.3411, -2.6807, 0.29678, 3.8845, 5.7014, 6.7526, 2.0576, 0.47953, 0.20421, 0.67861, 7.5435, 5.3436, 4.2415, 6.7981, 0.92695, 0.152, 2.8214, 1.8451, 4.2959, 7.2029, 1.9869, 0.14454, 9.0551, 0.61705])
(2)画出城市人口与利润图
通过 python 包 matplotlib.pyplot 画图
import matplotlib.pyplot as pltplt.scatter(x_train, y_train, marker='x', c='g') plt.title("利润*10000/人口数量*10000")
plt.ylabel('利润*10000')
plt.xlabel('人口数量*10000')plt.show()

(3)计算损失值
已知模型为:
fw⃗,b(x⃗(i))=w⃗⋅x⃗(i)+bf_{\vec{w},b}(\vec{x}^{(i)}) = \vec{w}·\vec{x}^{(i)}+bfw,b(x(i))=w⋅x(i)+b
损失函数为:
cost(i)=(fw⃗,b(x⃗(i))−y(i))2cost^{(i)} = (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2cost(i)=(fw,b(x(i))−y(i))2
总损失函数为:
J(w⃗.b)=12m∑i=0m−1cost(i)J(\vec{w}.b) = \frac 1 {2m} \sum ^{m-1} _{i=0} cost^{(i)}J(w.b)=2m1i=0∑m−1cost(i)
程序实现如下:
def compute_cost(x,y,w,b):m = x.shape[0]total_cost = 0.for i in range(m):f_wb = np.dot(w,x[i]) + bcost = (f_wb - y[i]) ** 2total_cost += costtotal_cost = total_cost / (2 * m)return total_cost
(4)计算梯度下降
梯度下降公式为:
repeat until convergence:{0000b:=b−α∂J(w,b)∂b0000w:=w−α∂J(w,b)∂w}\begin{align*}& \text{repeat until convergence:} \; \lbrace \newline \; & \phantom {0000} b := b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \; & \phantom {0000} w := w - \alpha \frac{\partial J(w,b)}{\partial w} \; & \newline & \rbrace\end{align*}repeat until convergence:{0000b:=b−α∂b∂J(w,b)0000w:=w−α∂w∂J(w,b)}
详解 gradient 部分为:
∂J(w,b)∂b=1m∑i=0m−1(fw,b(x(i))−y(i))∂J(w,b)∂w=1m∑i=0m−1(fw,b(x(i))−y(i))x(i)\frac{\partial J(w,b)}{\partial b} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \\ \frac{\partial J(w,b)}{\partial w} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) -y^{(i)})x^{(i)} ∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))∂w∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))x(i)
代码实现 gradient 部分:
def compute_gradient(x,y,w,b):m = x.shape[0]dj_dw = 0dj_db = 0for i in range(m):f_wb = np.dot(w,x[i]) + bdj_dw += (f_wb - y[i]) * x[i]dj_db += f_wb - y[i]dj_dw = dj_dw / mdj_db = dj_db / mreturn dj_dw, dj_db
代码实现梯度下降 gradient descent:
def gradient_descent(x,y,w_in,b_in,cost_function,gradient_function,alpha,num_iters):J_history = []w_history = []w = copy.deepcopy(w_in)b = b_infor i in range(num_iters):dj_dw, dj_db = gradient_function(x,y,w,b)w = w - alpha * dj_dwb = b - alpha * dj_dbif i<100000:cost = cost_function(x,y,w,b)J_history.append(cost)if i% math.ceil(num_iters/10) == 0: # math.ceil: 将传入的参数向上取整为最接近的整数w_history.append(w)print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f} ")return w, b, J_history, w_history
(5)开始训练
initial_w = 0.
initial_b = 0.
iterations = 1500
alpha = 0.01w,b,_,_ = gradient_descent(x_train ,y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations)
print("w,b found by gradient descent:", w, b)
(6)画出训练好的模型
因为我们已经训练完成模型,所以直接用参数 向量w 与 参数b 的值进行绘图:
m = x_train.shape[0]
predicted = np.zeros(m)for i in range(m):predicted[i] = w * x_train[i] + bplt.plot(x_train, predicted, c = "b")
plt.scatter(x_train, y_train, marker='x', c='g') plt.title("Profits*10000/Population*10000")
plt.ylabel('Profits*10000')
plt.xlabel('Population*10000')

(7)做出预测
predict1 = 3.5 * w + b
print('For population = 35,000, we predict a profit of $%.2f' % (predict1*10000))predict2 = 7.0 * w + b
print('For population = 70,000, we predict a profit of $%.2f' % (predict2*10000))
(8)完整代码
import copy
import math
import numpy as npx_train = np.array([6.1101, 5.5277, 8.5186, 7.0032, 5.8598, 8.3829, 7.4764, 8.5781, 6.4862, 5.0546, 5.7107, 14.164, 5.734, 8.4084, 5.6407, 5.3794, 6.3654, 5.1301, 6.4296, 7.0708, 6.1891, 20.27, 5.4901, 6.3261, 5.5649, 18.945, 12.828, 10.957, 13.176, 22.203, 5.2524, 6.5894, 9.2482, 5.8918, 8.2111, 7.9334, 8.0959, 5.6063, 12.836, 6.3534, 5.4069, 6.8825, 11.708, 5.7737, 7.8247, 7.0931, 5.0702, 5.8014, 11.7, 5.5416, 7.5402, 5.3077, 7.4239, 7.6031, 6.3328, 6.3589, 6.2742, 5.6397, 9.3102, 9.4536, 8.8254, 5.1793, 21.279, 14.908, 18.959, 7.2182, 8.2951, 10.236, 5.4994, 20.341, 10.136, 7.3345, 6.0062, 7.2259, 5.0269, 6.5479, 7.5386, 5.0365, 10.274, 5.1077, 5.7292, 5.1884, 6.3557, 9.7687, 6.5159, 8.5172, 9.1802, 6.002, 5.5204, 5.0594, 5.7077, 7.6366, 5.8707, 5.3054, 8.2934, 13.394, 5.4369])
y_train = np.array([17.592, 9.1302, 13.662, 11.854, 6.8233, 11.886, 4.3483, 12., 6.5987, 3.8166, 3.2522, 15.505, 3.1551, 7.2258, 0.71618, 3.5129, 5.3048, 0.56077, 3.6518, 5.3893, 3.1386, 21.767, 4.263, 5.1875, 3.0825, 22.638, 13.501, 7.0467, 14.692, 24.147, -1.22, 5.9966, 12.134, 1.8495, 6.5426, 4.5623, 4.1164, 3.3928, 10.117, 5.4974, 0.55657, 3.9115, 5.3854, 2.4406, 6.7318, 1.0463, 5.1337, 1.844, 8.0043, 1.0179, 6.7504, 1.8396, 4.2885, 4.9981, 1.4233, -1.4211, 2.4756, 4.6042, 3.9624, 5.4141, 5.1694, -0.74279, 17.929, 12.054, 17.054, 4.8852, 5.7442, 7.7754, 1.0173, 20.992, 6.6799, 4.0259, 1.2784, 3.3411, -2.6807, 0.29678, 3.8845, 5.7014, 6.7526, 2.0576, 0.47953, 0.20421, 0.67861, 7.5435, 5.3436, 4.2415, 6.7981, 0.92695, 0.152, 2.8214, 1.8451, 4.2959, 7.2029, 1.9869, 0.14454, 9.0551, 0.61705])import matplotlib.pyplot as pltplt.scatter(x_train, y_train, marker='x', c='g')plt.title("profits*10000/num(human in a city)*10000")
plt.ylabel('profits*10000')
plt.xlabel('num(human in a city)*10000')plt.show()def compute_cost(x, y, w, b):m = x.shape[0]total_cost = 0.for i in range(m):f_wb = np.dot(w, x[i]) + bcost = (f_wb - y[i]) ** 2total_cost += costtotal_cost = total_cost / (2 * m)return total_costdef compute_gradient(x,y,w,b):m = x.shape[0]dj_dw = 0dj_db = 0for i in range(m):f_wb = np.dot(w,x[i]) + bdj_dw += (f_wb - y[i]) * x[i]dj_db += f_wb - y[i]dj_dw = dj_dw / mdj_db = dj_db / mreturn dj_dw, dj_dbdef gradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters):J_history = []w_history = []w = copy.deepcopy(w_in)b = b_infor i in range(num_iters):dj_dw, dj_db = gradient_function(x, y, w, b)w = w - alpha * dj_dwb = b - alpha * dj_dbif i < 100000:cost = cost_function(x, y, w, b)J_history.append(cost)if i % math.ceil(num_iters / 10) == 0: # math.ceil: 将传入的参数向上取整为最接近的整数w_history.append(w)print(f"Iteration {i:4}: Cost {float(J_history[-1]):8.2f} ")return w, b, J_history, w_historyinitial_w = 0.
initial_b = 0.
iterations = 1500
alpha = 0.01w,b,_,_ = gradient_descent(x_train ,y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations)
print("w,b found by gradient descent:", w, b)m = x_train.shape[0]
predicted = np.zeros(m)for i in range(m):predicted[i] = w * x_train[i] + bplt.plot(x_train, predicted, c = "b")
plt.scatter(x_train, y_train, marker='x', c='g')plt.title("Profits*10000/Population*10000")
plt.ylabel('Profits*10000')
plt.xlabel('Population*10000')plt.show()predict1 = 3.5 * w + b
print('For population = 35,000, we predict a profit of $%.2f' % (predict1*10000))predict2 = 7.0 * w + b
print('For population = 70,000, we predict a profit of $%.2f' % (predict2*10000))
相关文章:

【机器学习】P10 从头到尾实现一个线性回归案例
这里写自定义目录标题(1)导入数据(2)画出城市人口与利润图(3)计算损失值(4)计算梯度下降(5)开始训练(6)画出训练好的模型(…...
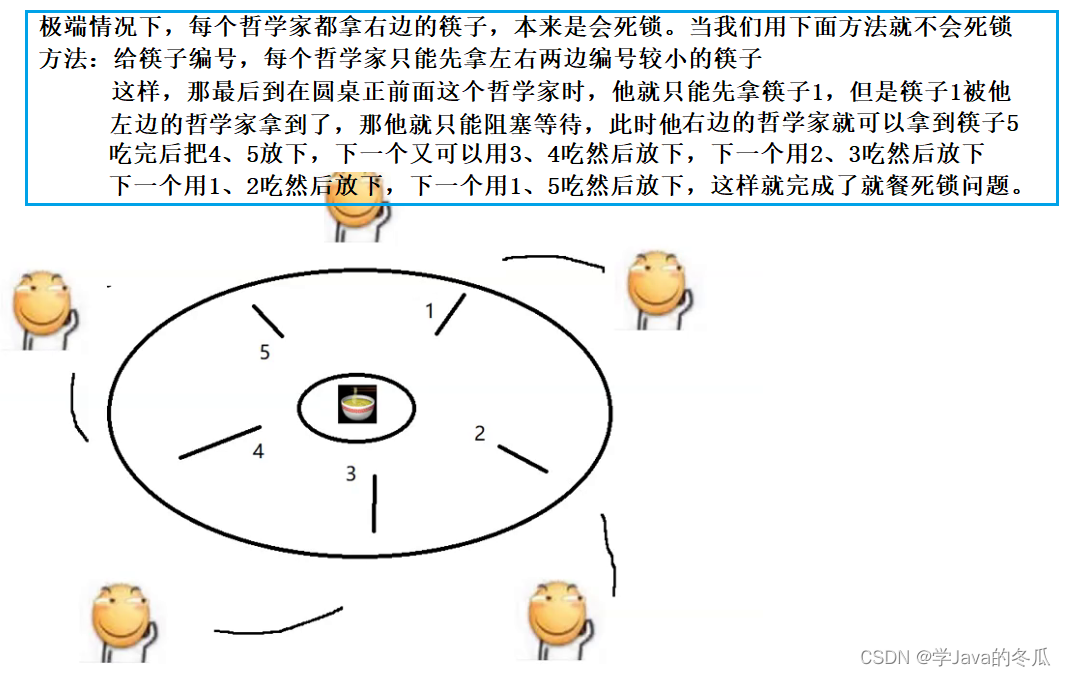
【Java EE】-多线程编程(四) 死锁
作者:学Java的冬瓜 博客主页:☀冬瓜的主页🌙 专栏:【JavaEE】 分享:2023.3.31号骑行的照片再发一次(狗头)。 主要内容:什么是死锁?不可重入可重入、死锁的三个典型情况:1、一个线程一…...
)
学习数据结构第1天(数据结构的基本概念)
数据结构的基本概念基本概念和术语数据结构的三要素经典试题基本概念和术语 1.数据 数据是信息的载体,是描述客观事物属性的数、字符以及所有能输入到计算机中并被计算机程序识别和处理的符号的集合。数据是计算机程序加工的原料。 2.数据元素 数据元素是数据的基本…...

南大通用数据库-Gbase-8a-学习-33-空洞率查询与解决方法
目录 一、个人理解 二、存储过程 三、虚机测试 四、解决方法 1、重建表 2、shrink space 一、个人理解 空洞率的产生是由于delete语句并不会真实的删除数据,只是在数据上打了一个不可见标签,但实际还是占用着相应的存储空间。 二、存储过程 自定义…...
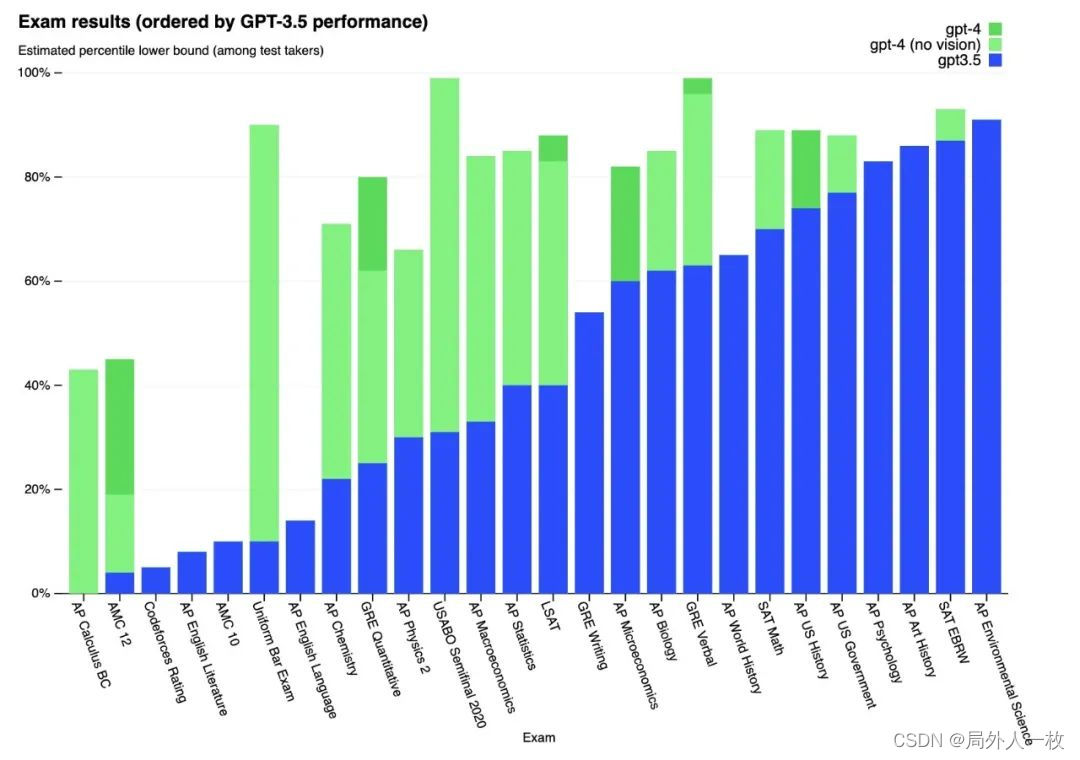
为什么我们认为GPT是一个技术爆炸
从23年初,ChatGPT火遍全球,通过其高拟人化的回答模式,大幅提升了人机对话的体验和效率,让用户拥有了一个拥有海量知识的虚拟助手,根据UBS发布的研究报告显示,ChatGPT在1月份的月活跃用户数已达1亿ÿ…...

程序员如何能提高自己的编程水平?
这些实用的小建议,能帮你迅速地提高编程水平: 不要做无意义的奋斗 拒绝喊口号和无意义的奋斗,包括但不限于: ①做了计划表却从未有执行的一天; ②每天都是最早来、最晚走,但是工作进度趋近于0;…...
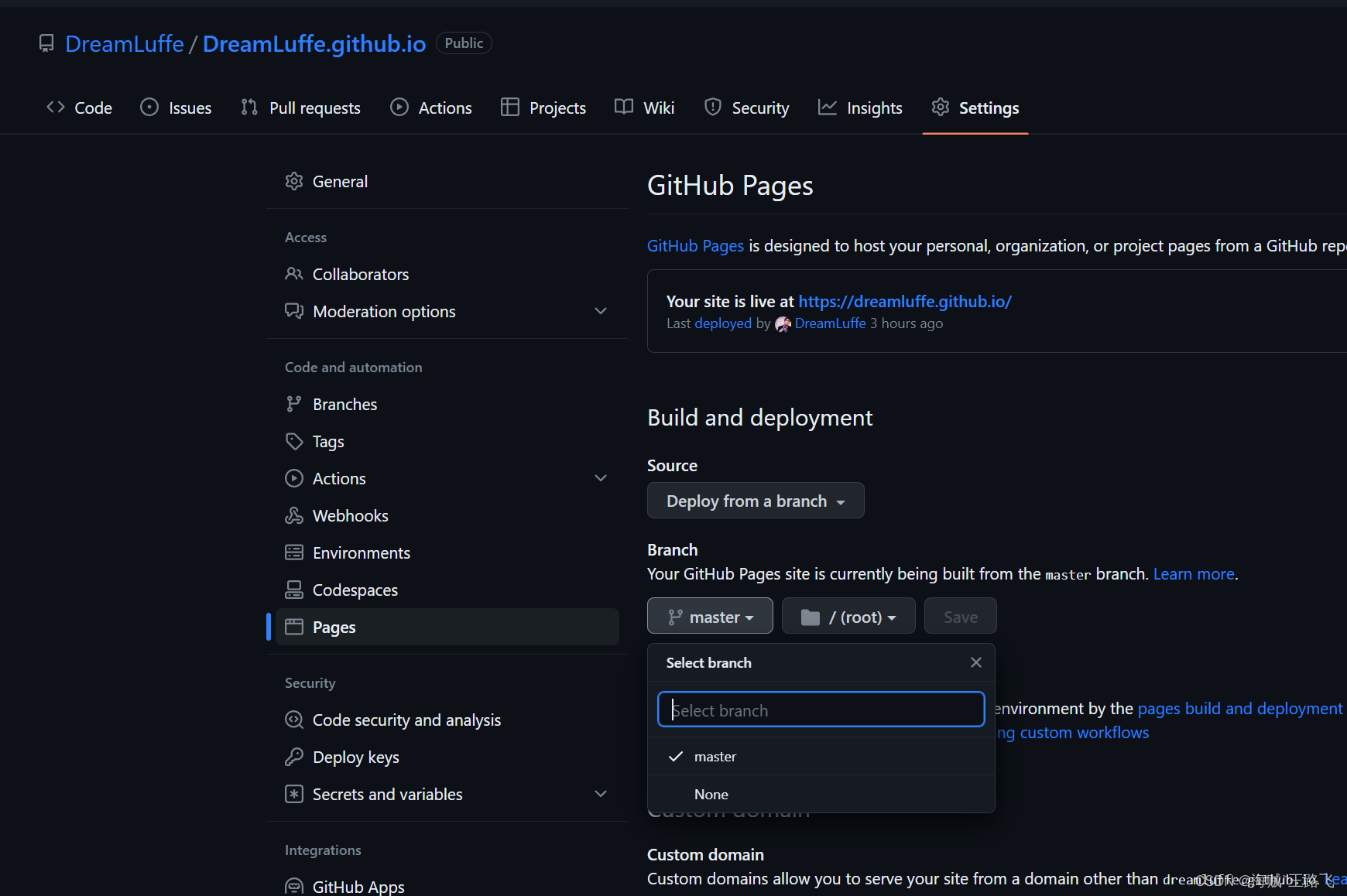
从零使用vuepress搭建个人博客部署.github.io
前言 记录小白如何搭建个人博客 github部署的博客👉: DreamLuffe的博客 netilify部署的博客:👉:DreamLuffe的博客 个人博客搭建实战 网上有很多优秀的开源博客页面,我们就直接安装好,再继续…...
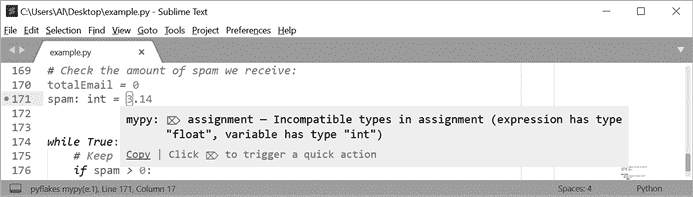
Python 进阶指南(编程轻松进阶):十一、注释、文档字符串和类型提示
原文:http://inventwithpython.com/beyond/chapter11.html 源代码中的注释和文档可能和代码一样重要。原因是软件是永远不会完成的;无论是添加新功能还是修复错误,您总是需要做出改变。但是你不能改变代码,除非你理解它࿰…...

python item()方法
Python中有很多方法来解决一些简单的问题,其中最常见的就是用 item ()方法来完成。item ()方法的全称是item-process (),该方法用来对对象进行创建、删除、改变、添加、更新等操作。…...

【day2】Android Jetpack Compose环境搭建
【day2】Android Jetpack Compose环境搭建 以下是适用于 Jetpack Compose 的环境要求: Android Studio 版本:4.2 Canary 15 或更高版本Gradle 版本:7.0.0-beta02 或更高版本Android 插件版本:4.2.0-beta15 或更高版本Kotlin 版本…...

stable-diffusion安装和简单测试
参考: https://github.com/CompVis/stable-diffusion 理解DALLE 2, Stable Diffusion和 Midjourney的工作原理 Latent Diffusion Models论文解读 【生成式AI】淺談圖像生成模型 Diffusion Model 原理 【生成式AI】Stable Diffusion、DALL-E、Imagen 背後…...
(附MATLAB代码实现))
MATLAB算法实战应用案例精讲-【智能优化算法】 基于帕累托包络的选择算法II(PESA-II)(附MATLAB代码实现)
目录 前言 知识储备 数据包络分析(DEA) 特点 名词解释 类型介绍 案例简介 软件操作(SPSSPRO)...

【华为机试真题详解JAVA实现】—坐标移动
目录 一、题目描述 二、解题代码 一、题目描述 开发一个坐标计算工具, A表示向左移动,D表示向右移动,W表示向上移动,S表示向下移动。从(0,0)点开始移动,从输入字符串里面读取一些坐标,并将最终输入结果输出到输出文件里面。 输入: 合法坐标为A(或者D或者W或者S) +…...

【软考五】数据库(做题)
该文章不适合学习数据库,适合考证,遇到实际问题的,不要在这儿浪费时间。切记切记 软考之数据库一、概念数据模型(下午题常考)二、结构数据模型关系模型1、关系模型中基本术语2、关系模型中的关系完整性约束3、关系代数…...

【Java Web】012 -- SpringBootWeb综合案例(登录功能、登录校验、异常处理)
目录 一、登录功能 1、基础登录功能 ①、SQL语句 ②、接口参数 ③、实现思路 ④、实现步骤 2、联调Bug(没有Cookie或Session) 二、登录校验 1、登录校验的实现思路 2、会话技术 ①、会话与会话跟踪 ②、会话跟踪方案对比 Cookie Session …...

跨界智能手表:比亚迪向左,小鹏向右
如今,电动化、智能化是汽车行业转型的大方向,而由于目前国内汽车产业在电动化方面已经算是“小有成效”,因此,抢占智能化高地,打造一个多设备互融的生态系统,就成为了车企的共同愿景。在此背景下࿰…...
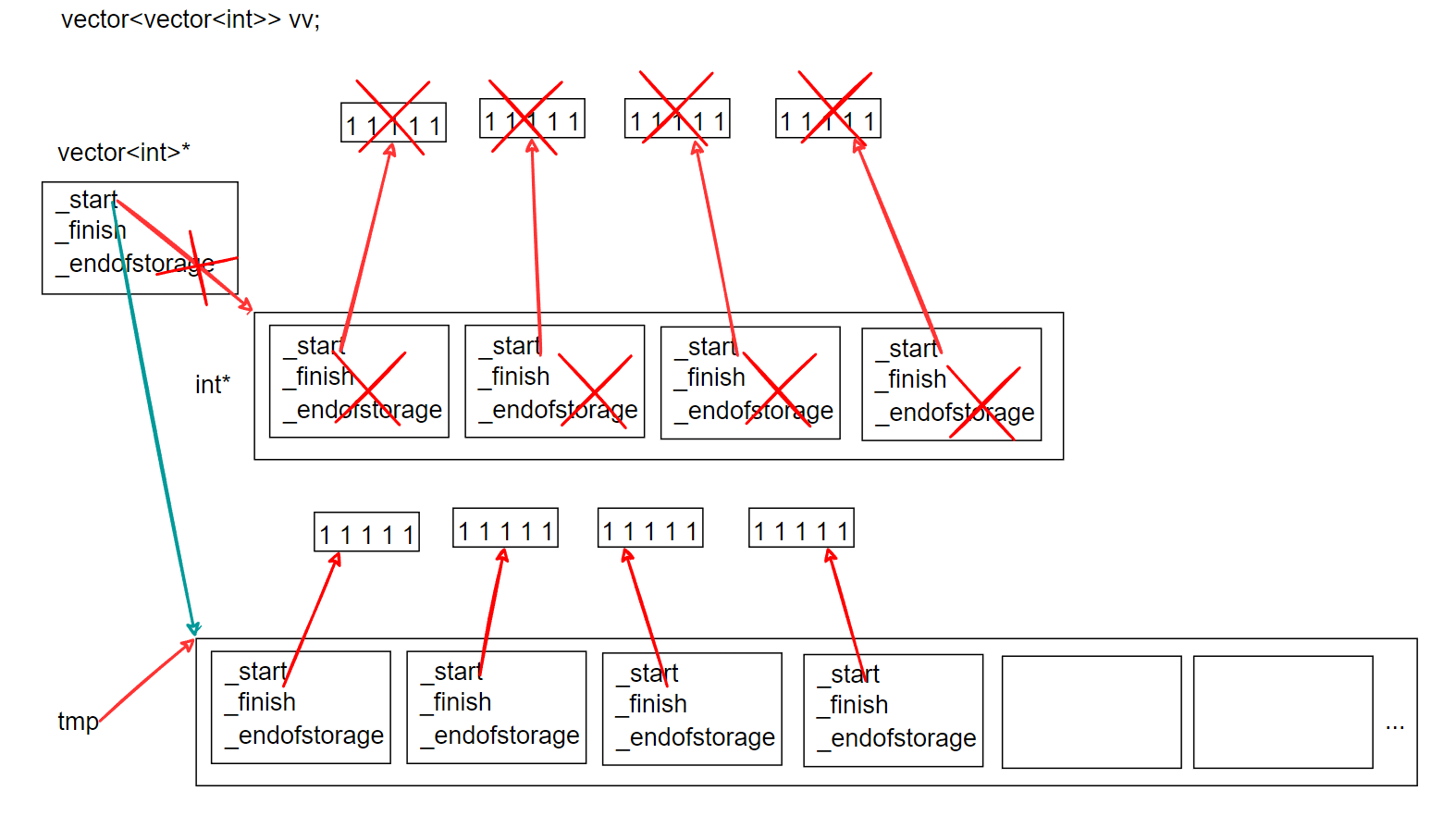
【c++初阶】第九篇:vector(常用接口的使用 + 模拟实现)
文章目录vector介绍vector的使用vector的定义vector iterator(迭代器) 的使用begin和endrbegin和rendvector 空间增长问题size和capacityreserve和resize(重点)测试vector的默认扩容机制emptyvector的增删查改push_back和pop_backinsert和erasefindswapo…...

Taro React组件使用(6) —— RuiSendCode 短信验证码【倒计时】
1. 需求分析 获取验证码按钮,点击后进入倒计时环节;默认采用 120s 后才允许再次发送短信验证码;发送后不能再次点击发送按钮,点击也不执行发送逻辑;最好将发送短信的业务逻辑请求接口写在组件中,封装为公用组件,可以多处使用。2. 实现效果 2.1 验证码发送前 2.2 验证码…...

把ChatGPT接入我的个人网站
效果图 详细内容和使用说明可以查看我的个人网站文章 把ChatGPT接入我的个人网站 献给有外网服务器的小伙伴 如果你本人已经有一台外网的服务器,并且页拥有一个OpenAI API Key,那么下面就可以参照我的教程来搭建一个自己的ChatGPT。 需要的环境 Cento…...

关于数字游民是未来年轻人工作趋势的一种思考
Q:我觉得未来,数字游民会是中国工作的一种主流方式,因为实体行业受到严重冲击,科技的发展是推导支持这样的远程工作形式,而且未来人的时间是越来越离散化、碎片化、原子化的,以订单交付的形式,P2P的形式会是…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
