蓝桥杯真题练习
小蓝在玩一个寻宝游戏, 游戏在一条笔直的道路上进行, 道路被分成了 nn 个方格, 依次编号 1 至 nn, 每个方格上都有一个宝物, 宝物的分值是一个整数 (包括正数、负数和零), 当进入一个方格时即获得方格中宝物的分值。小蓝可 以获得的总分值是他从方格中获得的分值之和。
小蓝开始时站在方格 1 上并获得了方格 1 上宝物的分值, 他要经过若干步 到达方格 nn。
当小蓝站在方格 pp 上时, 他可以选择跳到 p+1p+1 到 p+D(n-p)p+D(n−p) 这些方格 中的一个, 其中 D(1)=1, D(x)(x>1)D(1)=1,D(x)(x>1) 定义为 xx 的最小质因数。
给定每个方格中宝物的分值, 请问小蓝能获得的最大总分值是多少。
输入格式
输入的第一行包含一个正整数 nn 。
第二行包含 nn 个整数, 依次表示每个方格中宝物的分值。
输出格式
输出一行包含一个整数, 表示答案。
5
1 -2 -1 3 5
输出
8
本题一开始采用的动态规划,dp[i]表示在i位置的获得的最大价值。这是本人一开始的动态规划但是时间超时,只能换种方法。
for(int i=2;i<=n;i++){dp[i]=dp[i-1]+nums[i];for(int j=1;j<i;j++){int x=n-j;int m = m(x);if(m+j>=i)dp[i]=Math.max(dp[i],dp[j]+nums[i]);}}真题代码
public static void main(String[] args){Scanner scanner=new Scanner(System.in);int n=scanner.nextInt();int nums[]=new int[n+1];for(int i=1;i<=n;i++){nums[i]=scanner.nextInt();}int[] dp=new int[nums.length];Arrays.fill(dp,Integer.MIN_VALUE);dp[1]=nums[1];for(int i=1;i<=n;i++){int m=m(n-i);for(int j=i+1;j<=i+m;j++){dp[j]=Math.max(dp[j],dp[i]+nums[j] );}}System.out.println(dp[n]);}public static int m(int x){for(int i=2;i<=Math.sqrt(x);i++){if(x%i==0)return i;}return x;}
话说大诗人李白, 一生好饮。幸好他从不开车。
一天, 他提着酒显, 从家里出来, 酒显中有酒 2 斗。他边走边唱:
无事街上走,提显去打酒。 逢店加一倍, 遇花喝一斗。
这一路上, 他一共遇到店 NN 次, 遇到花 MM 次。已知最后一次遇到的是花, 他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序, 有多少种不同的可能?
注意: 显里没酒 ( 0 斗) 时遇店是合法的, 加倍后还是没酒; 但是没酒时遇 花是不合法的。
输入格式
第一行包含两个整数 NN 和 MM.
输出格式
输出一个整数表示答案。由于答案可能很大,输出模 1000000007 的结果.
样例输入
5 10样例输出
14
摘自蓝桥杯题解代码
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
//dp[n][m][k]表示遇见n店,m花,还剩k酒。
//因为题目要求最后一次必须是花,因此倒数第二次肯定剩余1数量的酒。
//所以答案ans = dp[n][m-1][1]。
//当剩余偶数酒的时候,有可能你上次遇见花也遇见店。
//当剩余奇数酒的时候,你上次必遇见店。
public class Main {public static final int mod = (int)1e9+7;public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n=scan.nextInt();int m=scan.nextInt();int[][][] dp = new int[n+1][m+1][m+5];dp[0][0][2]=1;dp[0][1][1]=1;dp[0][2][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k<=m;k++){if(i>0&&k>0&&k%2==0)dp[i][j][k]+=dp[i-1][j][k/2];if(j>0)dp[i][j][k]+=dp[i][j-1][k+1];dp[i][j][k]%=mod;}}}System.out.println(dp[n][m][0]%mod);scan.close();}
}相关文章:

蓝桥杯真题练习
小蓝在玩一个寻宝游戏, 游戏在一条笔直的道路上进行, 道路被分成了 nn 个方格, 依次编号 1 至 nn, 每个方格上都有一个宝物, 宝物的分值是一个整数 (包括正数、负数和零), 当进入一个方格时即获得方格中宝物的分值。小蓝可 以获得的总分值是他从方格中获得的分值之和。 小蓝开始…...

插入排序的简单理解
详细描述 插入排序的基本思想是:将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增 1 的有序表。 在其实现过程中使用双层循环,外层循环针对除了第一个元素之外的所有元素,内层循环针对当前元素前面的有序表进行…...

Springboot框架集成Websocket通信方式
Websocket实现了“服务器”主动向“客户端”发送数据,改变了以往通过轮询、长轮训、长连接等方式获取服务器端数据的方式。 一、Websocket有三种不同的用场景,单播、广播和组播; (一)、单播(Unicast) 单播是客户端与服务器之间的“一对一”的连接。是在一个单个的发送…...

将json数据分组
在工作中有时需要根据业务需要,将大量数据进行处理分成几个一组 // 例如要将下方数据进行处理 var stuCount [{"id": "1612321835288","libraryCode": "D","regionCode": "A","positionCode&qu…...

从零开始实现一个C++高性能服务器框架----Socket模块
此项目是根据sylar框架实现,是从零开始重写sylar,也是对sylar丰富与完善 项目地址:https://gitee.com/lzhiqiang1999/server-framework 简介 项目介绍:实现了一个基于协程的服务器框架,支持多线程、多协程协同调度&am…...

ld: library not found for -lcrt0.o
ld: library not found for -lcrt0.o 背景: Mac 系统编译的时候报错 语言:golang 原因: 代码使用了静态编译,-static。stack overflow 上说 This option will not work on Mac OS X unless all libraries (including libgcc.a…...
接口测试和功能测试的区别有哪些?说一些你不知道的知识
目录 接口测试和功能测试的区别 目的 测试范围 测试方法 重要性 编辑 举个例子 对于接口测试 对于功能测试 编辑 总结 接口测试和功能测试是软件测试中的两种常见测试类型,主要用于评估软件系统的质量。尽管这两种测试都是为了评估软件系统的性…...
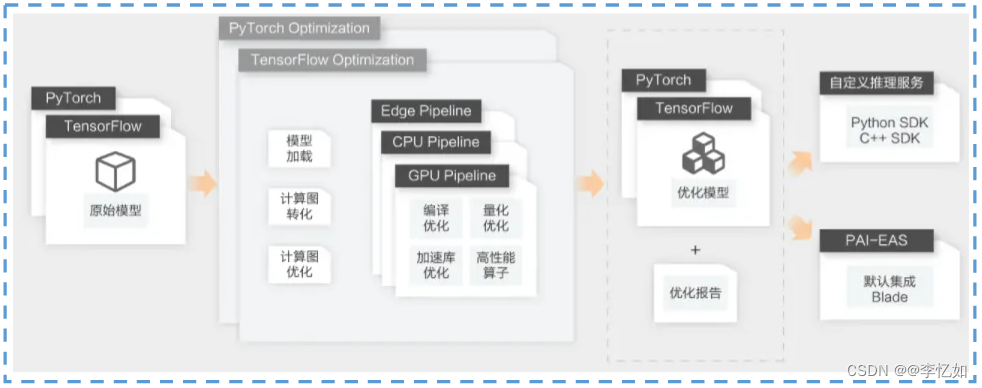
深度学习实战——不同方式的模型部署(CNN、Yolo)
忆如完整项目/代码详见github:https://github.com/yiru1225(转载标明出处 勿白嫖 star for projects thanks) 目录 系列文章目录 一、实验综述 1.实验工具及及内容 2.实验数据 3.实验目标 4.实验步骤 二、ML/DL任务综述与模型部署知识…...

【论文阅读】GNN阅读笔记
A gentle introduction on gnn 前言 发表在distill的文章 图神经网络在应用上才刚刚开始 搭建了一个GNN playground 什么是图 图是表示实体之间的关系 可以分别表示成点向量、边向量、图向量 图可以分为有向图和无向图 数据是怎么表示成图 图片表示成图: …...
,QTableWidget控件)
QT常用控件——QTreeWidget(树控件),QTableWidget控件
目录 ★先开个小灶,在此插句话:【有关Halcon与Qt联编变量转换】 QTreeWidget树控件 QTableWidget控件...

为什么学校购买小型数控机床而不是大型工业数控机床?
CNC 机器是计算机控制的设备,可以高精度和准确度地切割、雕刻、钻孔或雕刻各种材料。 它们广泛应用于制造、工程、设计和艺术行业。 CNC 机器具有不同的尺寸和功能,从小型台式机到大型工业机型。 人们可能想知道为什么学校会选择购买小型 CNC 机器而不是…...

【Go自学】一文搞懂Go append方法
我们先看一下append的源码 // The append built-in function appends elements to the end of a slice. If // it has sufficient capacity, the destination is resliced to accommodate the // new elements. If it does not, a new underlying array will be allocated. //…...
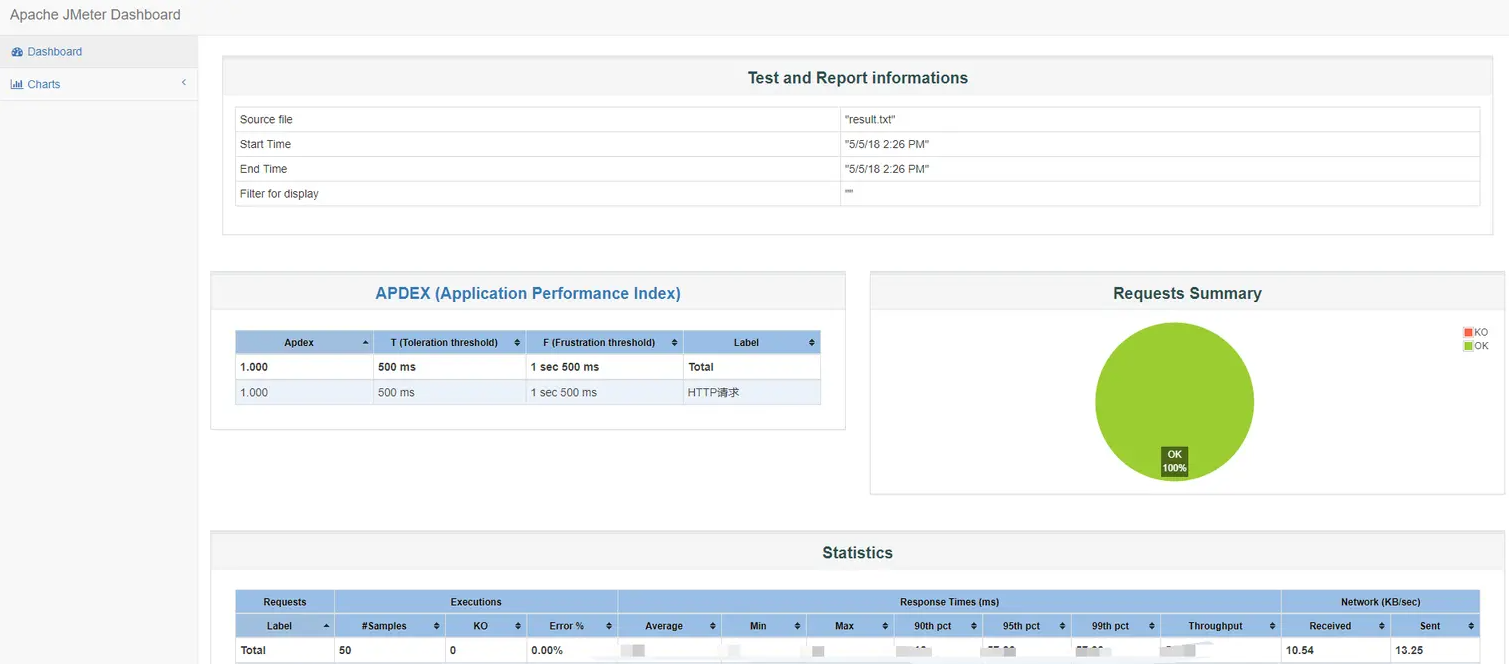
【压测】通过Jemeter进行压力测试(超详细)
文章目录背景一、前言二、关于JMeter三、准备工作四、创建测试4.1、创建线程组4.2、配置元件4.3、构造HTTP请求4.4、添加HTTP请求头4.5、添加断言4.6、添加察看结果树4.7、添加Summary Report4.8、测试计划创建完成五、执行测试计划总结背景 通过SpringCloudGateway整合Nacos进…...
加密算法)
C# | 上位机开发新手指南(七)加密算法
上位机开发新手指南(七)加密算法 文章目录上位机开发新手指南(七)加密算法前言加密算法的分类对称加密算法和非对称加密算法流加密算法和块加密算法分组密码和序列密码哈希函数和消息认证码对称加密与非对称对称加密优点缺点对称加…...
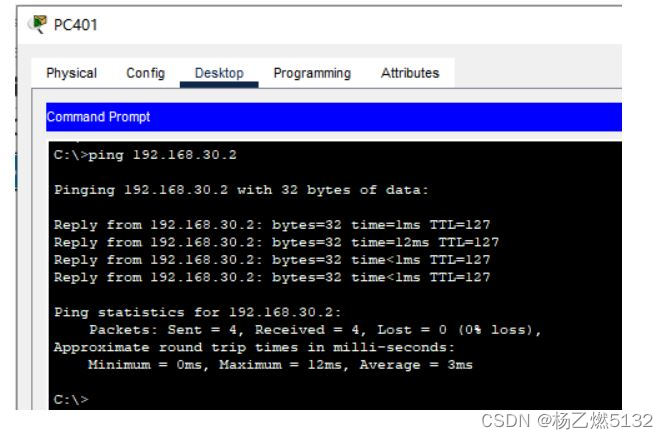
实验一 跨VLAN访问
目录 一、按照拓扑图配置VLAN,并实现跨VLAN间的访问。 二、实验环境 三、实验步骤 一、按照拓扑图配置VLAN,并实现跨VLAN间的访问。 1、配置好交换机的VLAN和各个终端的地址,实现各个VLAN内能连通。 2、开启两个交换机的VTY连接࿰…...

通信算法之130:软件无线电-接收机架构
1. 超外差式接收机 2.零中频接收机 3.数字中频接收机...

C++编程大师之路:从入门到精通-C++基础入门
文章目录前言主要内容C基础入门初识C第一个C程序注释变量常量关键字标识符命名规则数据类型整型sizeof关键字实型(浮点型)字符型转义字符字符串型布尔类型 bool数据的输入运算符算术运算符赋值运算符比较运算符逻辑运算符程序流程结构选择结构if语句三目…...
如何在千万级数据中查询 10W 的数据并排序
前言 在开发中遇到一个业务诉求,需要在千万量级的底池数据中筛选出不超过 10W 的数据,并根据配置的权重规则进行排序、打散(如同一个类目下的商品数据不能连续出现 3 次)。 下面对该业务诉求的实现,设计思路和方案优…...

RocketMQ消息文件过期原理
文章目录 消费完后的消息去哪里了?什么时候清理物理消息文件?这样设计带来的好处跳过历史消息的处理所有的消费均是客户端发起Pull请求的,告诉消息的offset位置,broker去查询并返回。但是有一点需要非常明确的是,消息消费后,消息其实并没有物理地被清除,这是一个非常特殊…...
Docker容器理解
目录 目录 一:简单理解操作系统 操作系统: 内核: 内核空间和用户空间: 二:简单理解文件系统 1:什么是文件系统 2:什么是root文件系统 三:docker 1:docker镜像 2&…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
