Python:青蛙跳杯子(BFS)
题目描述
X 星球的流行宠物是青蛙,一般有两种颜色:白色和黑色。
X 星球的居民喜欢把它们放在一排茶杯里,这样可以观察它们跳来跳去。
如下图,有一排杯子,左边的一个是空着的,右边的杯子,每个里边有一只青蛙。
∗WWWBBB
其中,W 字母表示白色青蛙,B 表示黑色青蛙,∗ 表示空杯子。
X 星的青蛙很有些癖好,它们只做 3 个动作之一:
-
跳到相邻的空杯子里。
-
隔着 1 只其它的青蛙(随便什么颜色)跳到空杯子里。
-
隔着 2 只其它的青蛙(随便什么颜色)跳到空杯子里。
对于上图的局面,只要 1 步,就可跳成下图局面:
WWW∗BBB
本题的任务就是已知初始局面,询问至少需要几步,才能跳成另一个目标局面。
输入描述
输入为 2 行,2 个串,表示初始局面和目标局面。我们约定,输入的串的长度不超过 15。
输出描述
输出要求为一个整数,表示至少需要多少步的青蛙跳。
输入输出样例
示例
输入
*WWBB
WWBB*
输出
2思路:
参考代码:
import sys
chushi = input()
mubiao = input()
lis = [1,-1,2,-2,3,-3]
experience = {chushi} #标记状态
queue= [[chushi,0]] #状态和层数
while queue: #若不为空old = queue.pop(0) #弹出第一个元素for i in lis:state = list(old[0]) #字符串转化为列表step = old[1]kgwz = state.index('*') #查找空格位置xkgwz = kgwz + i #新空格位置if 0<=xkgwz<len(chushi): #判断新空格位置是否出界state[kgwz] = state[xkgwz]state[xkgwz] = '*'new_state = "".join(state)step += 1if new_state == mubiao:print(step)sys.exit(0) #程序终止if new_state not in experience: #若新状态没有出现过以前的状态中experience.add(new_state)queue.append([new_state,step])相关文章:
)
Python:青蛙跳杯子(BFS)
题目描述 X 星球的流行宠物是青蛙,一般有两种颜色:白色和黑色。 X 星球的居民喜欢把它们放在一排茶杯里,这样可以观察它们跳来跳去。 如下图,有一排杯子,左边的一个是空着的,右边的杯子,每个…...

6.10 谱分解
文章目录计算方法代码实现计算方法 单纯矩阵normal matrix指的是符号ATAAATA^TAAA^TATAAAT的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。 对于单纯矩阵,存在以下的谱定理Spectral theorem&…...

MySQL入门篇-MySQL 行转列小结
备注:测试数据库版本为MySQL 8.0 需求:求emp表各个岗位的工资之和,如无,用0代替 如需要scott用户下建表及录入数据语句,可参考:scott建表及录入数据sql脚本 CASE语法 SELECT deptno,ifnull(sum(case when job MANAGER then sal else 0 …...

项目管理常见的十大难题及其症状
01缺少维护文档时常,项目工作紧张时,第一个去掉的就是文档工作。有时即使项目有时间,也不会创建文档;或是创建了文档,却很少在项目进行过程中维护它。症状产品与需求文档不符;技术文档过时,无法保证技术的延…...

技术方案模板
0.基本原则 1.可量化,很大、很多、很高 到底是多少?基本没影响,到底有没有影响什么情况下有影响? 2.可实施,结合实际情况最终可落地 3.可指导,非方案制定人能理解,能在尽量少的人工沟通的情况下实现方案 4.可复用,设计的方案,再次出现类似需求时可以做到少开发或不…...

MySQL中对于单表和多表的操作
一、单表查询素材: 表名:worker-- 表中字段均为中文,比如 部门号 工资 职工号 参加工作 等显示所有职工的基本信息。mysql8.0 [chap03]>select * from worker;查询所有职工所属部门的部门号,不显示重复的部门号。mysql8.0 [cha…...

MFI认证
一、什么是MFI认证? 苹果MFI认证,是苹果公司(Apple Inc.)对其授权配件厂商生产的外置配件的一种使用许可,MFi认证是apple公司Made for iPhone/iPad/iPod的英文缩写。是指分别为连接iPhone/iPad/iPod而特别设计的电子配件。 [图片] 二、iOS外设连接的几种方式 [图片] 这…...

Vue中mixins的使用
文章目录mixins介绍mixins特点mixins介绍 Mixins:在引入组件之后与组件中的对象和方法进行合并,相当于扩展了父组件的对象与方法,可以理解为形成了一个新的组件。混入 (mixins):是一种分发 Vue 组件中可复用功能的非常灵活的方式…...
【PyQt】PyQt学习(一)框架介绍+环境搭建
简介 写在最前面的话 在决定学习、使用一个框架之前需要考量如下几点: 框架运行效果;框架应用范围;框架学习成本和迁移成本;实现自己所需功能的开发效率; 只有综合考量如上四个方面,才能更好地选择适合…...

浅谈前端设计模式:策略模式和状态模式的异同点
一、策略模式 策略模式是定义一系列的算法,把它们一个个封装起来, 并且使它们可相互替换。 而且策略模式是重构小能力,特别适合拆分“胖逻辑”。 这个定义乍一看会有点懵,不过通过下面的例子就能慢慢理解它的意思。 先来看一个真实场景 某次活动要做…...

线性杂双功能PEG试剂OPSS-PEG-Acid,OPSS-PEG-COOH,巯基吡啶聚乙二醇羧基
英文名称:OPSS-PEG-COOH,OPSS-PEG-Acid 中文名称:巯基吡啶-聚乙二醇-羧基 OPSS-PEG-COOH是一种具有OPSS和羧基的线性杂双功能PEG试剂。它是一种有用的带有PEG间隔基的交联剂。OPSS代表正吡啶基二硫化物或邻吡啶基二硫代,与硫醇、…...

开发微服务电商项目演示(四)
一,网关服务限流熔断降级第1步:启动sentinel-dashboard控制台和Nacos注册中心服务第2步:在网关服务中引入sentinel依赖<!-- sentinel --> <dependency><groupId>com.alibaba.cloud</groupId><artifactId>sprin…...
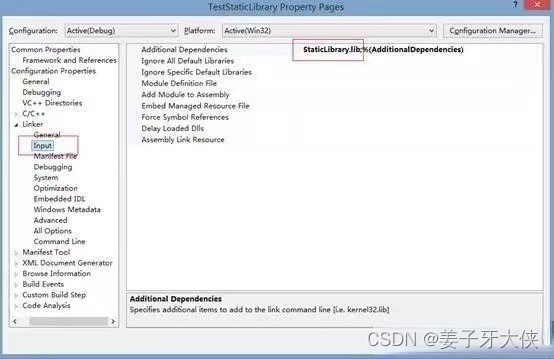
【C语言学习笔记】:静态库
一、什么是库 库是写好的现有的,成熟的,可以复用的代码。现实中每个程序都要依赖很多基础的底层库,不可能每个人的代码都从零开始,因此库的存在意义非同寻常。 本质上来说库是一种可执行代码的二进制形式,可以被操作…...

社科院与杜兰大学中外合作办学金融管理硕士——30+的年龄在职读研有必要吗?
说起读研,年龄在什么区间最合适呢?上次有位咨询的同学反馈年龄已经快35岁了,有一份不错的工作,但又不甘心止步于此,想要通过提升学历升职加薪,但又纠结自己是否能静下心来学习、是否能顺利毕业、拿到的证书…...
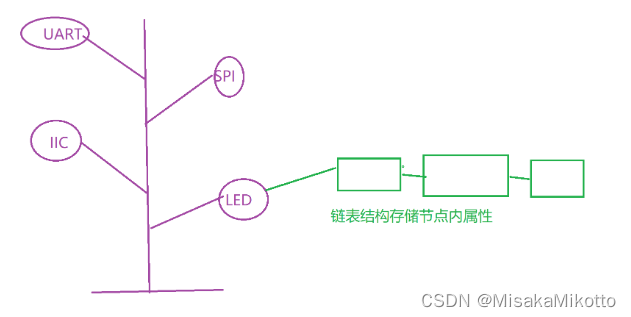
2.13作业【设备树解析,按自己理解】
设备树定义 设备树(device tree是描述硬件信息的一种树形结构,设备书文件在linux内核启动后被内核解析。描述一个硬件设备信息的节点我们叫做设备节点,一个设备节点内部包含当前硬件的多个不同属性,相同节点不同属性是以链式结构存…...

《NFL星计划》:巴尔的摩乌鸦·橄榄1号位
巴尔的摩乌鸦(英语:Baltimore Ravens)是一支职业美式橄榄球球队位于马里兰州的巴尔的摩。他们现时为美国美式橄榄球联合会的北区进行比赛,其主场为M&T银行体育场。乌鸦队曾在2000年和2012年取得超级碗冠军。 巴尔的摩乌鸦 成…...
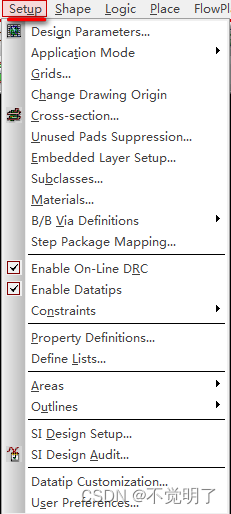
Allegro如何设置自动保存和自动保存的时间操作指导
Allegro如何设置自动保存和自动保存的时间操作指导 做PCB设计的时候,自动保存软件是一个必要的功能,Allegro同样支持设置自动保存,而且可以设置自动保存的时间。 如下图 具体操作如下 点击Setup点击User Preferences...
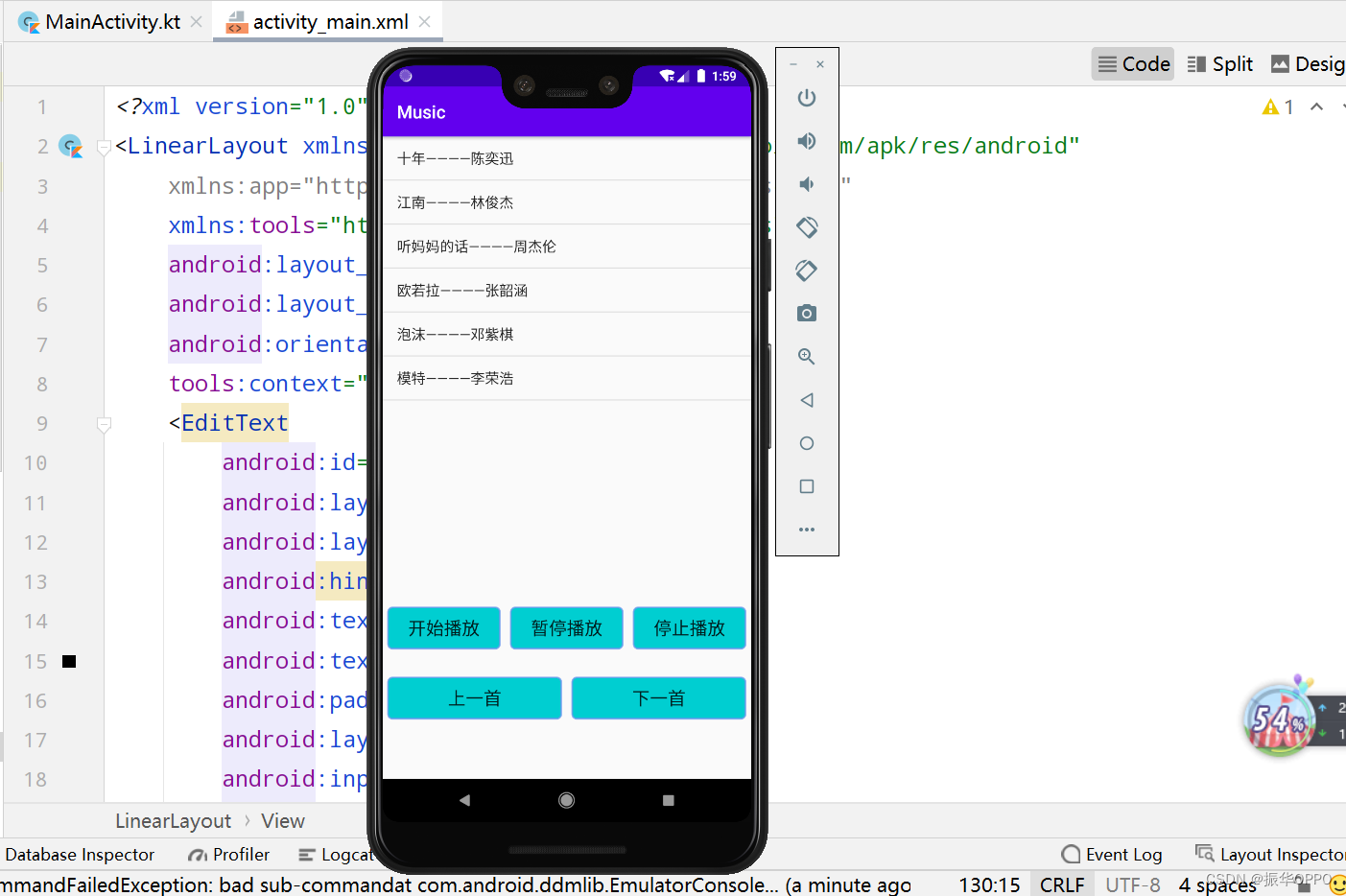
Kotlin实现简单音乐播放器
关于音乐播放器,我真的是接触比较多,听歌作为我第一大爱好,之前也用Java设计过音乐播放器,感兴趣的同学可以阅读:Android Studio如何实现音乐播放器(简单易上手)和 Android Studio实现音乐播放器…...
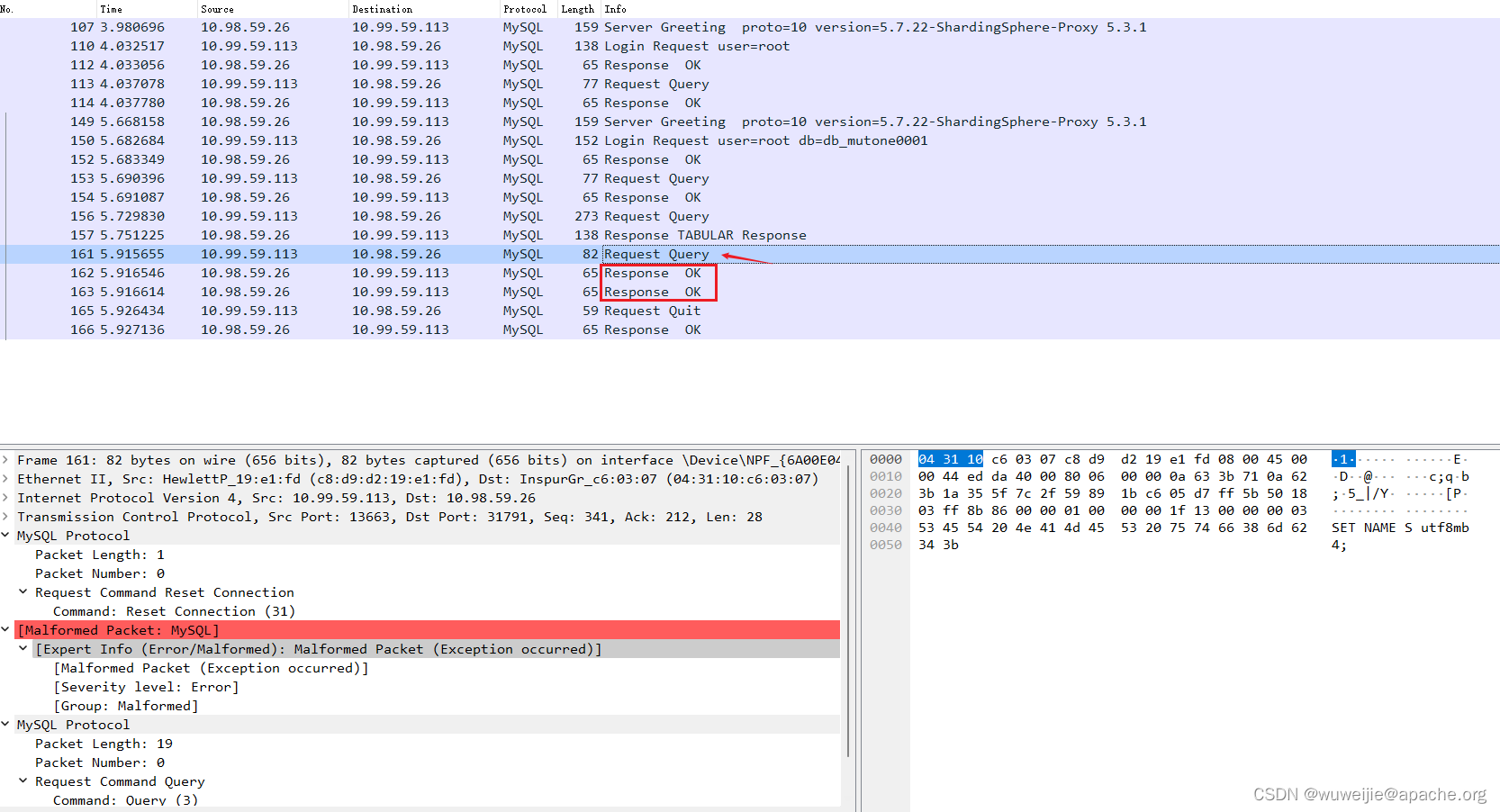
ShardingSphere-Proxy 数据库协议交互解读
数据库协议对于大部分开发者来说算是比较冷门的知识,一般的用户、开发者都是通过现成的数据库客户端、驱动使用数据库,不会直接操作数据库协议。不过,对数据库协议的特点与流程有一些基本的了解,有助于开发者在排查数据库功能、性…...
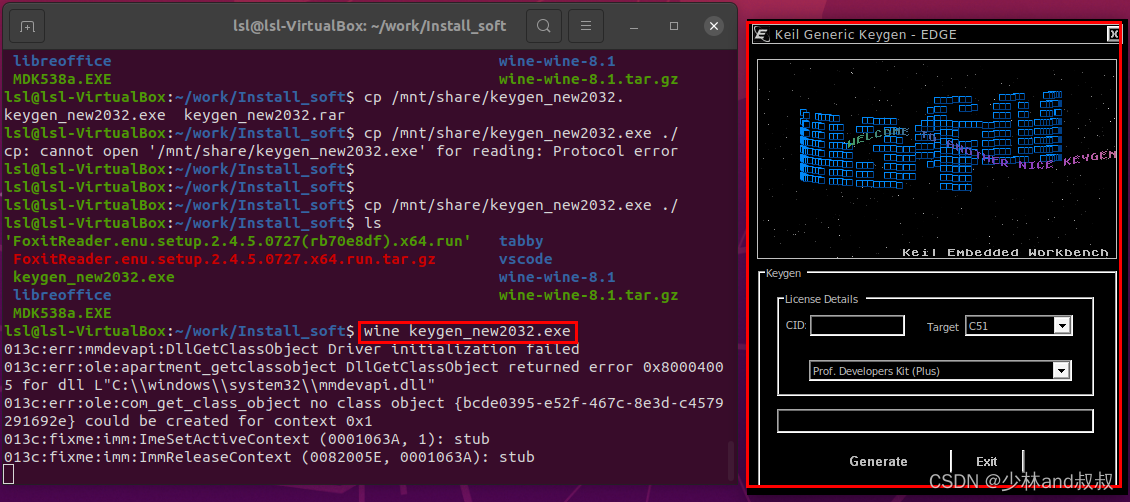
基于ubuntu20.4的wine的MDK5软件的安装
本文基于ubuntu20.4安装MDK5的keil软件,由于MDK不提供linux版本的安装软件,因此需要利用wine软件来安装MDK5软件,具体流程包括wine软件安装、MDK5安装及MDK5的lic添加等3部分内容。具体流程如下所示: (一)…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
