电动力学问题中的Matlab可视化
电磁场的经典描述
小说一则
- 电磁场的经典描述就是没有啥玩意量子力学的经典电动力学下对电磁场的描述,以后有空写个科幻小说,写啥呢,就写有天张三遇见了一个外星人,外星人来自这样一个星球,星球上的物质密度特别低,导致外星人的测量会明显的影响物质的运动,外星人不能同时得到动量与位置啊啥的......
- 外星人很希望有一天能找到一个不那么量子力学的世界(这依然是经典的"量子观")
- 张三是个优秀的气象工作员,搞出来的全是李雅普诺夫不稳定的数学模型
- 张三见了外星人表示很好,咱们臭味相投啊
- 外星人表示,是的,学数学物理,物理数学有啥意思呢,不如享受当下的生活
- 张三表示,好哇好哇,好个锤子哇,我们要探索宇宙,你不觉得李雅普诺夫的理论很过时吗,不够先进啦
- 外星人表示:我说一个像是反驳了但是没有成功反驳的话啊:李雅普诺夫是苏俄时期逝世的
- 张三表示:...........
- 外星人表示:还是要好好学习哇!
四个方程组
麦克斯韦方程组
电磁物质方程组
电磁边值方程组
势场边值方程组
电势
库伦规范下的磁矢势
(旋度的旋度=散度的散度-拉普拉斯算子)
磁标势
数据可视化
重要提示
- 不论是数据可视化还是数值计算
- 都不可能替代你的理论分析过程
- 永远是你先得到了一个差不多的结果,才去做数值分析,可视化等等。
- 数据可视化常常受限于你的计算机和人眼
- 不要太较真
常见绘图语言
- 一些常见符号不再赘述
流线 Streamlines
将矢量平滑得连接起来的不相交的曲线
matlab代码----Copyright 2015 The MathWorks, Inc.
[x,y] = meshgrid(0:0.1:1,0:0.1:1);
u = sin(x);
v = -cos(y);figure
quiver(x,y,u,v)startx = 0.1:0.1:1;
starty = ones(size(startx));
streamline(x,y,u,v,startx,starty)matlab 语法
streamline(X,Y,Z,U,V,W,startx,starty,startz)
streamline(U,V,W,startx,starty,startz)
streamline(XYZ)
streamline(X,Y,U,V,startx,starty)
streamline(U,V,startx,starty) 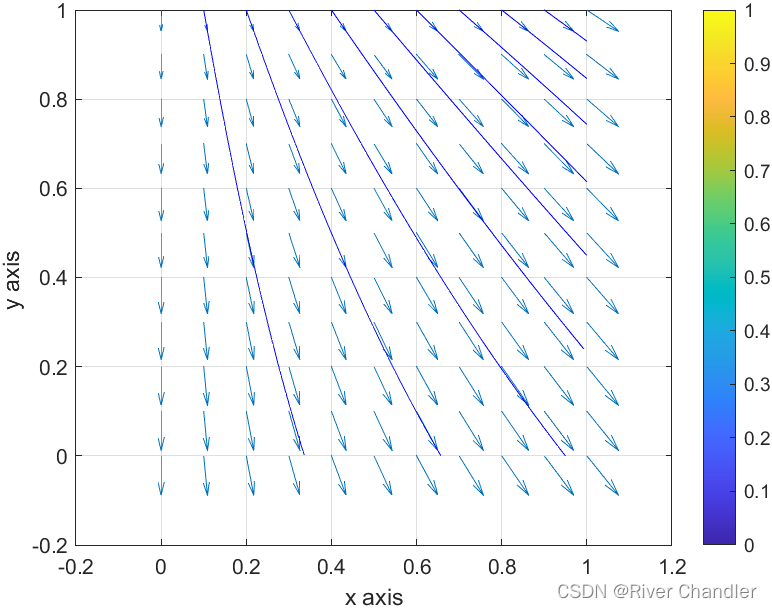
等值线
连接值相等的多个点的不相交的封闭曲线
x = linspace(-2*pi,2*pi);
y = linspace(-2*pi,2*pi);
[X,Y] = meshgrid(x,y);
Z = tan(X)-cos(Y);
contour(X,Y,Z)
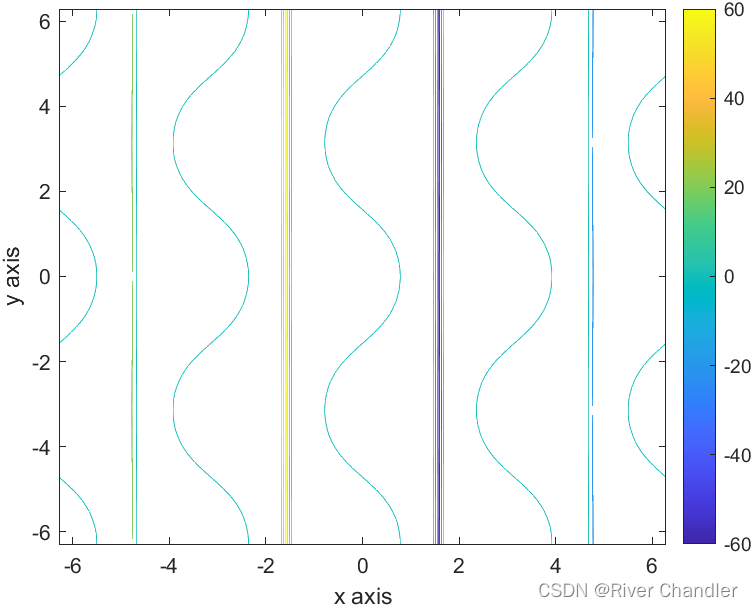
matlab 语法
contour(X,Y,Z,'线型',等高线表示的值)数据可视化案例一:匀强电场中的电导体球

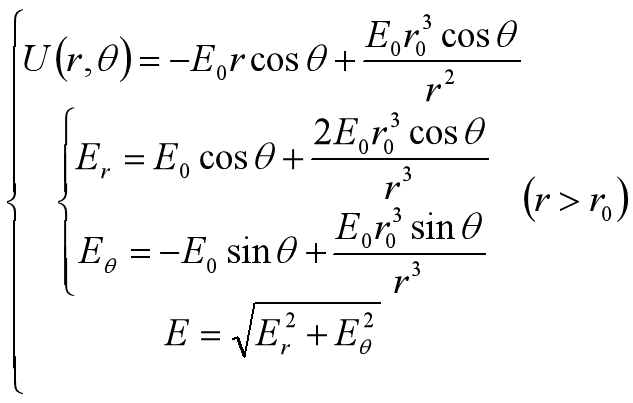
数据可视化案例二:匀强电场中的电介质球
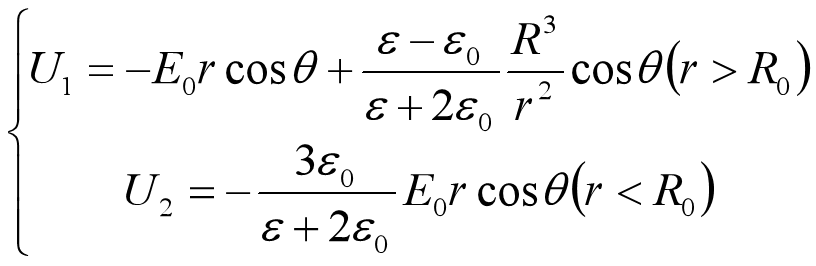
相关文章:
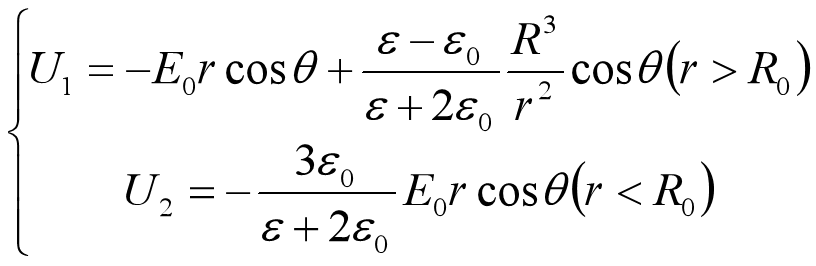
电动力学问题中的Matlab可视化
电磁场的经典描述 小说一则 电磁场的经典描述就是没有啥玩意量子力学的经典电动力学下对电磁场的描述,以后有空写个科幻小说,写啥呢,就写有天张三遇见了一个外星人,外星人来自这样一个星球,星球上的物质密度特别低,导致外星人的测量会明显的影响物质的运动,外星人不能同时得到…...

云原生周刊:编程即将终结?
近日哈佛大学计算机科学的前教授 Matt Welsh,分享了他对计算机科学、分布式计算的未来以及 ChatGPT 和 GitHub Copilot 是否代表编程结束的开始的看法。 威尔士说,编程语言仍然很复杂。再多的工作也无法让它变得简单。 “在我看来,任何改进…...

C++ STL,resize 和 reserve 的区别
结论放前边:resize和reserve都可以给容器扩容,区别在于resize会进行填充,使容器处于满员的状态,即sizecapacity,而reserve不会填充,有size<capacity. 1. size 和 capacity 的区别 size和capacity是容器…...

Java——详解ReentrantLock与AQS的关联以及AQS的数据结构和同步状态State
前言 Java中大部分同步类(Lock、Semaphore、ReentrantLock等)都是基于AbstractQueuedSynchronizer(简称为 AQS)实现的。 AQS 是一种提供了原子式管理同步状态、阻塞和唤醒线程功能以及队列模型的简单框架。 本文会先介绍应用层&a…...

vue3+vite+ts 接入QQ登录
说明 前提资料准备 在QQ互联中心注册成为开发者 站点:https://connect.qq.com/创建应用,如图 js sdk方式 下载对应的sdk包 sdk下载:https://wiki.connect.qq.com/sdk%e4%b8%8b%e8%bd%bd 使用 下载离线js sdk 打开:https:…...
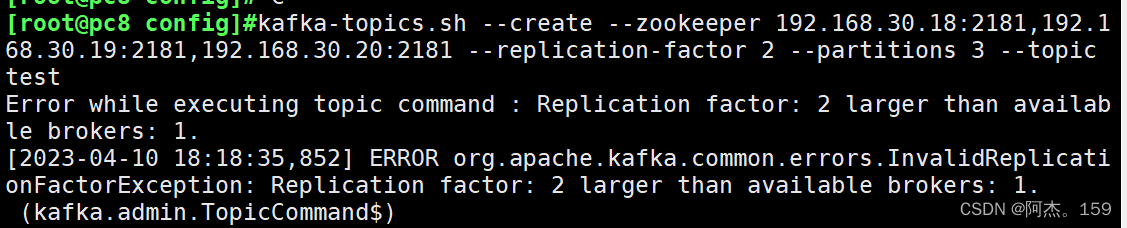
消息队列kafka及zookeeper机制
目录 一、zookeeper 1、zookeeper简介 2、zookeeper特点 3、zookeeper工作模式及机制 4、zookeeper应用场景及选举机制 5、zookeeper集群部署 ①实验环境 ②安装zookeeper 二、消息队列kafka 1、为什么要有消息队列 2、使用消息队列的好处 3、kafka简介 4、kafka…...
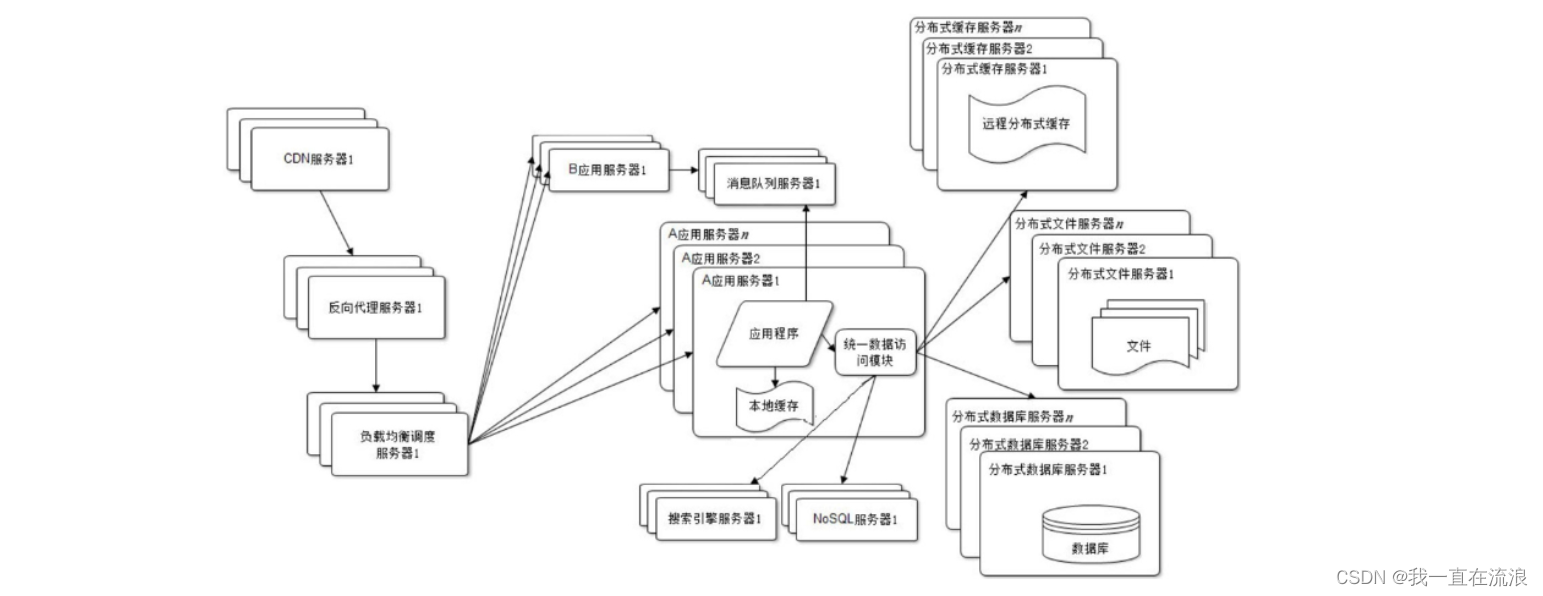
分布式 - 分布式体系架构:IT架构的演进过程
文章目录01. 应用与数据一体模式02. 应用服务和数据服务的分离03. 缓存与性能的提升04. 服务器集群处理并发05. 数据库读写分离06. 反向代理和 CDN07. 分布式文件系统和分布式数据库系统08. NoSQL和搜索引擎09. 业务拆分10. Redis缓存在应用服务器上是进程内缓存还是进程外缓存…...

CSDN 周赛42期
CSDN 周赛42期1、题目名称:鬼画符门之宗门大比2、题目名称:K皇把妹3、题目名称:影分身4、题目名称:开心的金明小结1、题目名称:鬼画符门之宗门大比 给定整数序列A。 求在整数序列A中连续权值最大的子序列的权值。 &…...

Vue:初识Vue
1、首先要导入vue.js <!-- 当你使用script标签安装vue之后,上下文就注册了一个全局变量vue --><script src"../1.Vue/js/vue.js"></script> 不能直接调用vue(),需要new vue(),否则会报错。 2、关于vue构造函数的参数opti…...
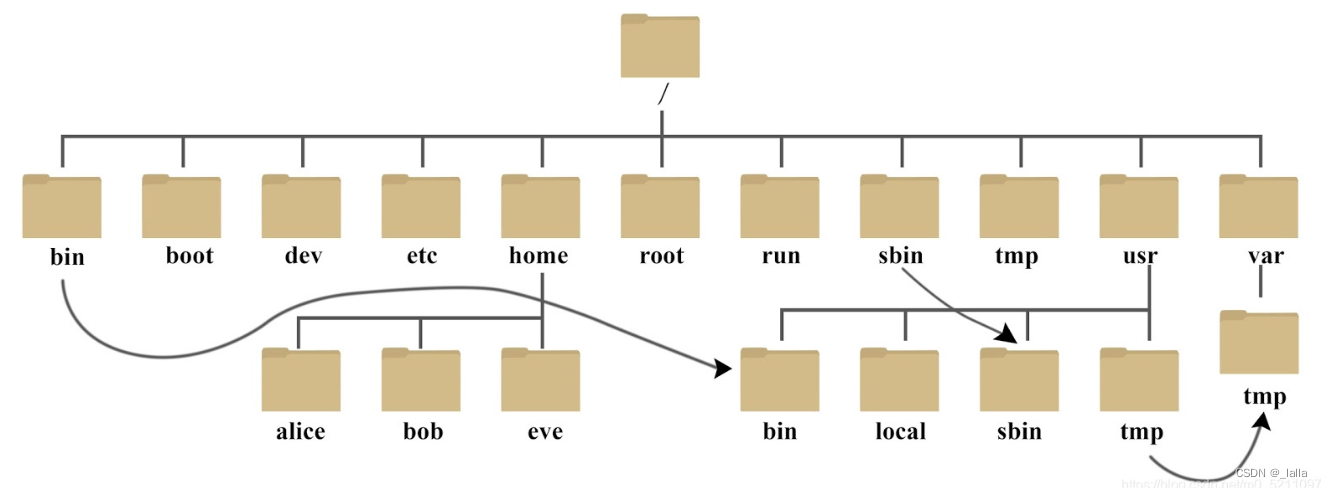
linux语言学习记录
文章目录前言一、linux文件结构二、指令三、Gvim编辑器1、命令模式2、底行命令四、正则表达式1、表达式匹配举例2、对文件里面内容进行操作3、使用 \( 和 )\ 符号括起正规表达式,即可在后面使用\1和\2等变量来访问和中的内容前言 记录自己学习linux的笔记ÿ…...
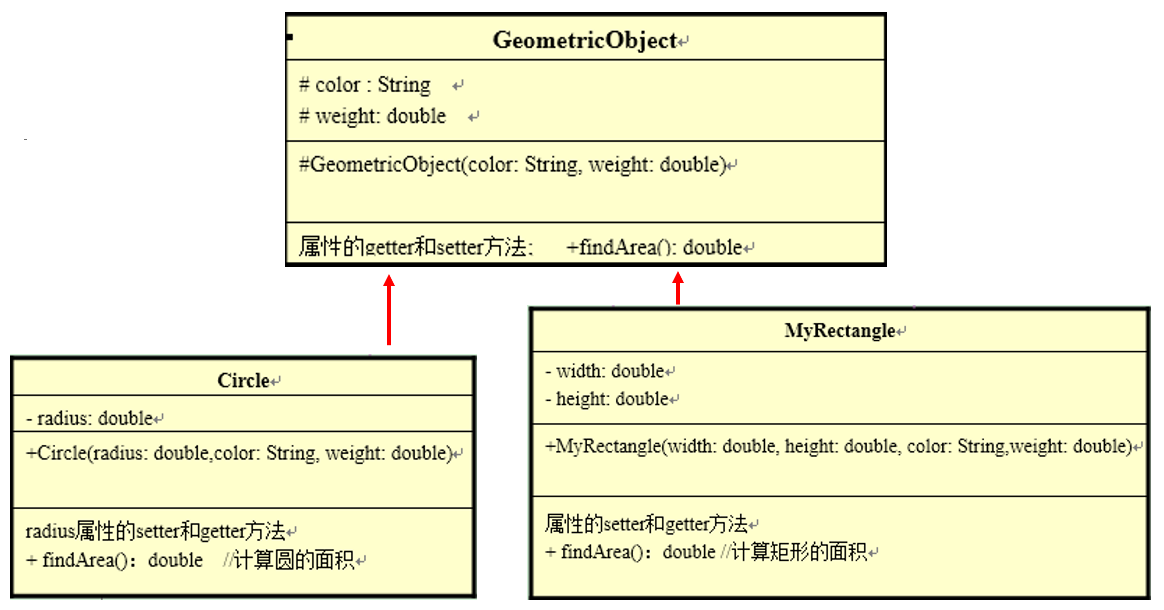
面向对象编程(进阶)7:面向对象特征三:多态性
一千个读者眼中有一千个哈姆雷特。 目录 7.1 多态的形式和体现 7.1.1 对象的多态性 举例: 7.1.2 多态的理解 7.1.3 举例 1、方法内局部变量的赋值体现多态 2、方法的形参声明体现多态 3、方法返回值类型体现多态 7.2 为什么需要多态性(polymorphism)&#x…...

vue尚品汇商城项目-day04【29.加入购物车操作(难点)】
文章目录29.加入购物车操作(难点)29.1加入购物车按钮29.2addCartSuce29.3购物车29.3.1 向服务器发送ajax请求,获取购物车数据29.3.2UUID临时游客身份29.3.3动态展示购物车29.4修改购物车产品的数量(需要发请求:参数理解…...

KubeSphere 社区双周报 | 4.8 深圳站 Meetup 火热报名中 | 2023.3.17-3.30
KubeSphere 社区双周报主要整理展示新增的贡献者名单和证书、新增的讲师证书以及两周内提交过 commit 的贡献者,并对近期重要的 PR 进行解析,同时还包含了线上/线下活动和布道推广等一系列社区动态。 本次双周报涵盖时间为:2023.03.17-2023.…...

ChatGPT热炒之前 搜索引擎SEO算法已经悄然改变
2022年4月起,某度算法有了新的调整,这对于靠SEO获得流量的公司简直可以说是灭顶之灾。原本SEO从业者还指望跟之前一样,等算法调整稳定后,网站的自然排名还会再回来,但等到了10月份,仍然没有回暖的迹象&…...

【Linux】Mysql之视图的基本操作
一、什么是视图 MySQL 视图(View)是一种虚拟存在的表,同真实表一样,视图也由列和行构成, 但视图并不实际存在于数据库中。行和列的数据来自于定义视图的查询中所使用的 表,并且还是在使用视图时动态生成的。…...

《扬帆优配》西藏地震!美史上最严排放新规将出台,美股收涨
当地时间周四,美股遍及收高,科技股领涨。因耶稣受难日,美股4月7日(周五)休市,周四为美股本周最终一个买卖日,从本周状况来看,纳指与标普500指数均录得跌幅,别离跌1.1%和0…...

Python 小型项目大全 66~70
六十六、简单替换密码 原文:http://inventwithpython.com/bigbookpython/project66.html 简单替换密码用一个字母代替另一个字母。由于字母A有 26 种可能的替换,B有 25 种可能的替换,C有 24 种可能的替换,等等,所以可能…...
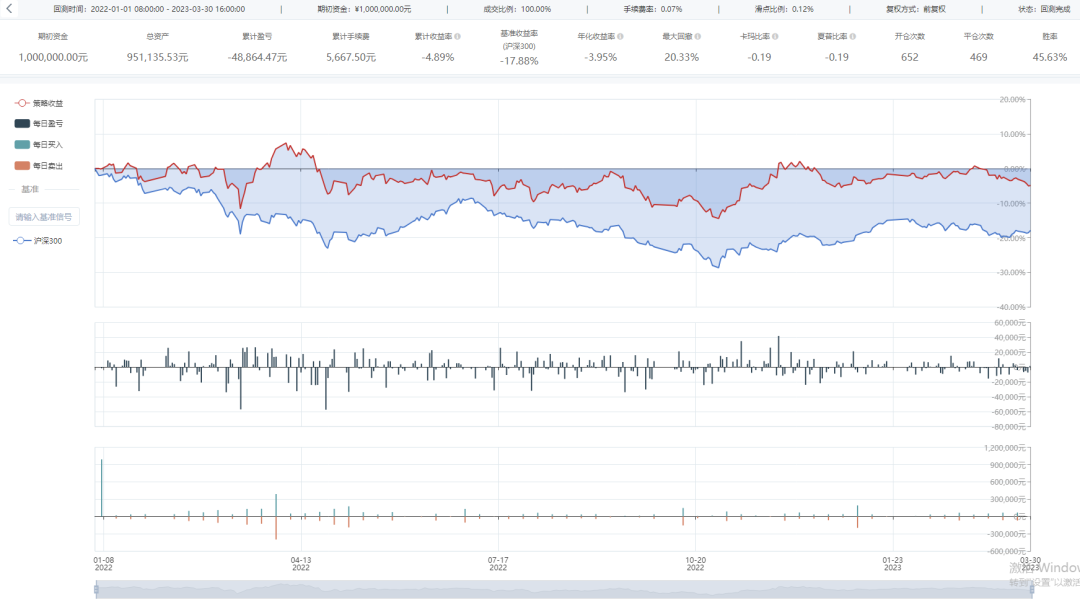
Barra模型因子的构建及应用系列八之Earning_Yeild因子
一、摘要 在前期的Barra模型系列文章中,我们构建了Size因子、Beta因子、Momentum因子、Residual Volatility因子、NonLinear Size因子、Book-to-Price因子和Liquidity因子,并分别创建了对应的单因子策略,其中Size因子和NonLinear Siz因子具有…...

2022蓝桥杯省赛——卡片
问题描述 小蓝有 k 种卡片, 一个班有 n 位同学, 小蓝给每位同学发了两张卡片, 一位同学的两张卡片可能是同一种, 也可能是不同种, 两张卡片没有顺序。没有两位同学的卡片都是一样的。 给定 n, 请问小蓝的卡片至少有多少种? 输入格式 输入一行包含一个正整数表示 n 。 输出…...

数据结构-快速排序
一.概要 快速排序是一种基于分治思想的排序算法,其基本思路是选取一个基准值(pivot),通过一趟排序将待排序列分成两个部分,其中左半部分都小于基准值,右半部分都大于基准值,然后对左右两部分分…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
