Heap堆的升序排序
在heap堆中,大根堆是一种特殊的堆,它满足下列性质:对于任意一个非叶子节点i,其左右子节点的值均小于等于它本身的值。
在大根堆中,堆顶元素永远是值最大的元素,所以将堆顶元素不断取出来,就相当于对数组进行了从大到小的排序操作。
相比较于其他排序算法,使用大根堆进行数组排序的优点在于:
1:时间复杂度稳定为O(nlogn),空间复杂度仅为O(1),并且算法实现简洁、易于理解。
2:由于大根堆的特殊性质,堆排序还具有良好的局部性和稳定性,能够保持元素在排序前后的相对位置关系,不会改变具有相同值的元素之间的顺序。
下面用图片来梳理我们的思路
代码注解
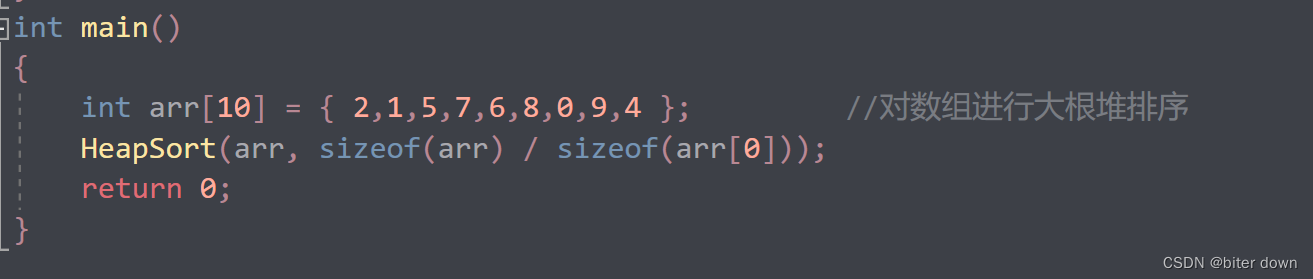
首先我们先创建一个数组:
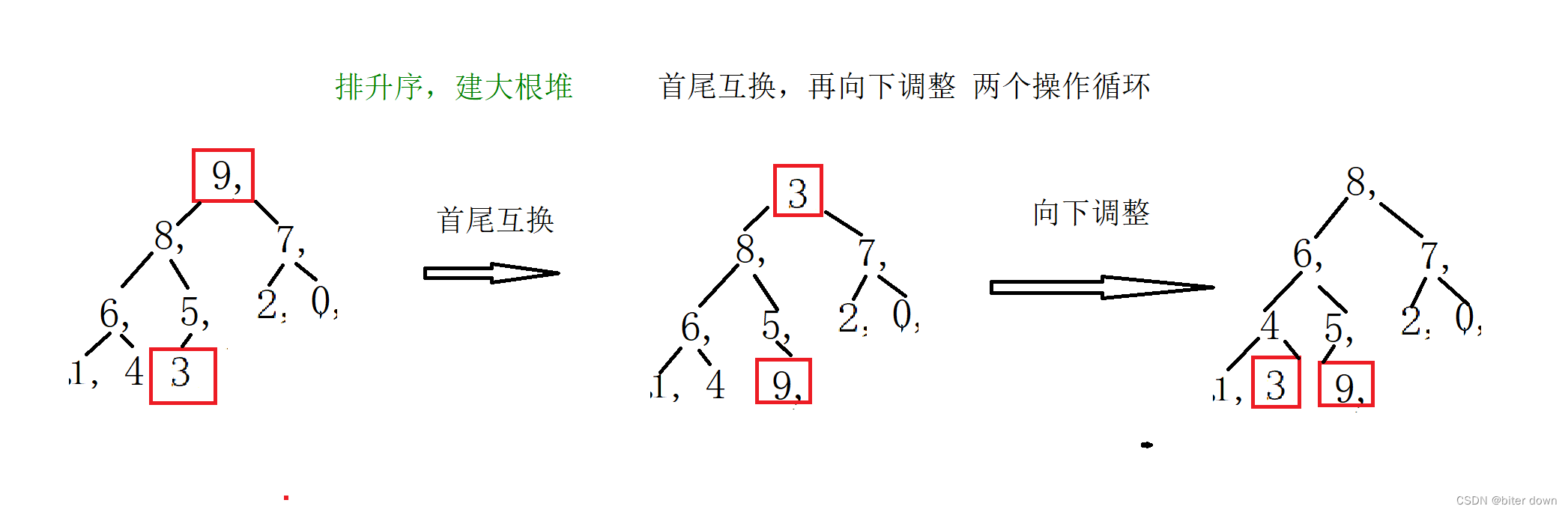
1: 首先我们将数组中的值建立成大根堆
2:首尾换位,向下调整成为循环
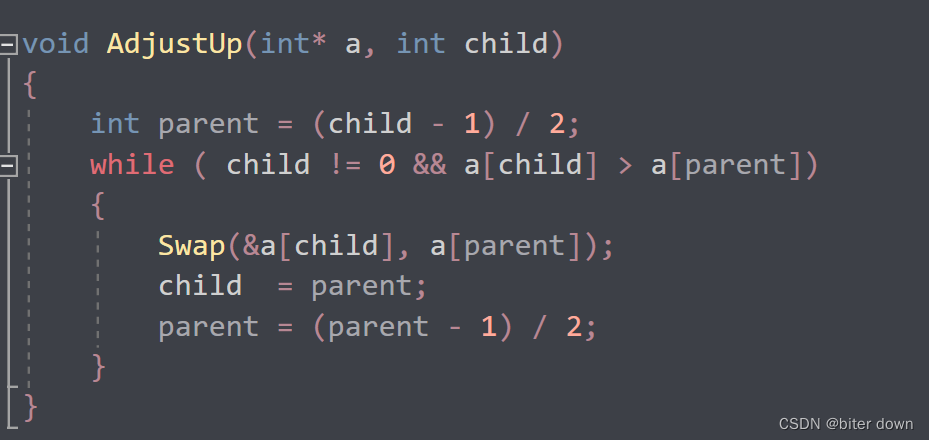
我们将数组中的值建立成大根堆的Adjustup函数的实现
Adjustup函数的实现的空间复杂度(3条消息) 堆的向下调整与向上调整的时间复杂度_biter down的博客-CSDN博客
我们将数组中的值建立成大根堆的Adjustup函数的实现
Adjustdown函数的实现的空间复杂度(3条消息) 堆的向下调整与向上调整的时间复杂度_biter down的博客-CSDN博客
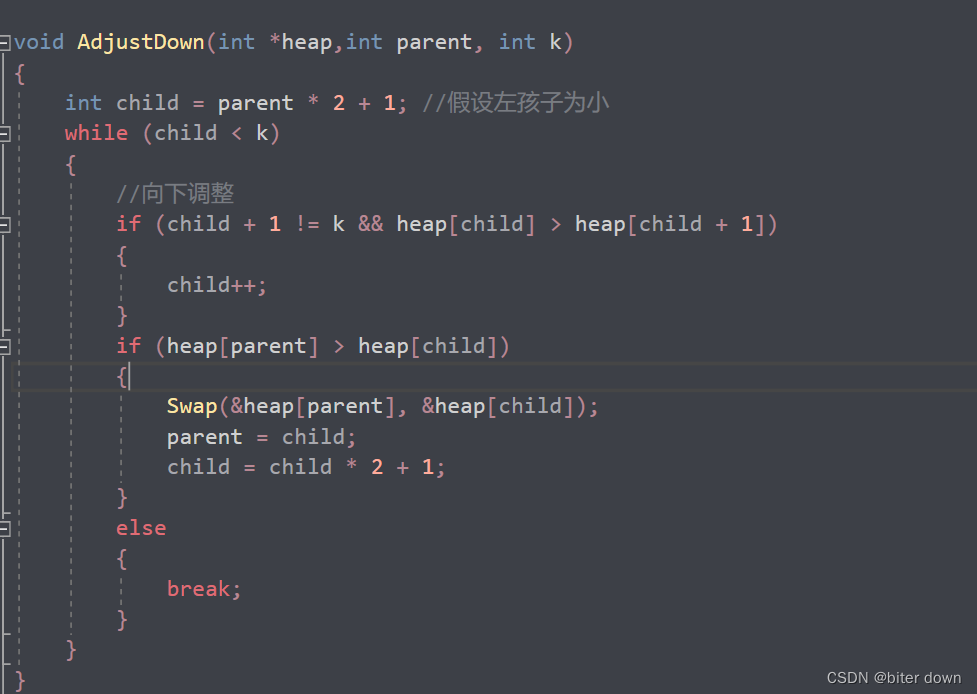
源码提供参考:
#include<stdio.h>
void Swap(int* p1, int* p2) {
int t = *p1;
*p1 = *p2;
*p2 = t;
}
void AdjustDown(int* a, int size) {
int parent = 0;
//将leftchild作为最大的孩子
int child = parent * 2 + 1;
while (child < size)
{
//当leftchild的值小于rightchlid时,child的值应该为较大值的右孩子
if (child + 1 < size && a[child + 1] > a[child])
{
child++;
}
Swap(&a[child], a[parent]);
parent = child;
child = child * 2 + 1;
}
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
while ( child != 0 && a[child] > a[parent])
{
Swap(&a[child], a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
}
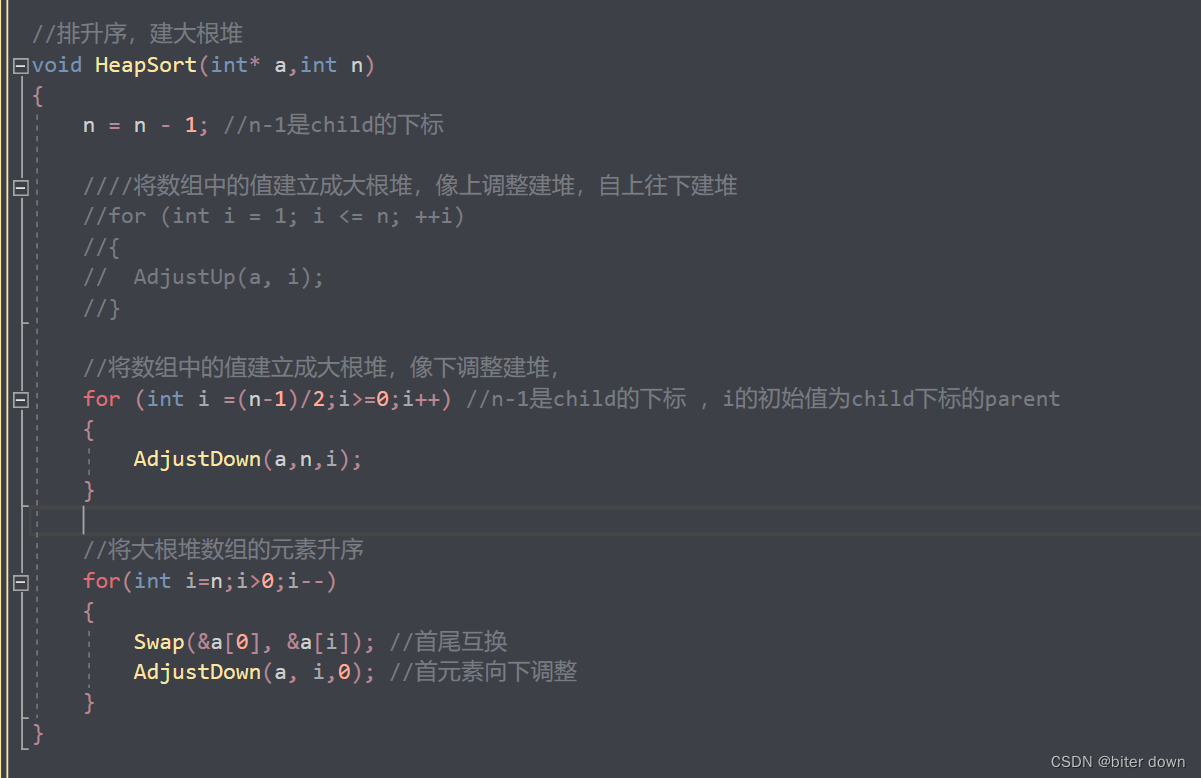
//排升序,建大根堆
void HeapSort(int* a,int n)
{
//将数组中的值建立成大根堆
for (int i = 1; i < n; ++i)
{
AdjustUp(a, i);
}
//将大根堆数组的元素升序
for(int i=n;i>0;i--)
{
Swap(&a[0], &a[i]); //首尾互换
AdjustDown(a, i); //向下调整
}
}
int main()
{
int arr[10] = { 2,1,5,7,6,8,0,9,4 }; //对数组进行大根堆排序
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
return 0;
}
相关文章:

Heap堆的升序排序
在heap堆中,大根堆是一种特殊的堆,它满足下列性质:对于任意一个非叶子节点i,其左右子节点的值均小于等于它本身的值。 在大根堆中,堆顶元素永远是值最大的元素,所以将堆顶元素不断取出来,就相当…...
小程序开发收费价目表
小程序作为一种新兴应用形式,正在逐渐成为企业和个人推广、运营的重要手段。然而,小程序开发的价格因项目规模和复杂程度差异较大,令不少人望而却步。本文将从小程序开发的相关因素入手,探讨小程序开发的价格范围和算法。 一、小…...

Dubbo服务暴露步骤详解
文章目录Dubbo服务暴露步骤详解背景介绍理论知识讲解什么是服务暴露?Dubbo 服务暴露的基本原理操作步骤具体实现环境准备实现服务接口实现服务提供者配置 Dubbo 服务提供者启动服务提供者实现服务消费者配置 Dubbo 服务消费者测试总结Dubbo服务暴露步骤详解 背景介…...

第十四届蓝桥杯编程题部分代码题解
C. 冶炼金属 最大值就是取 a/ba / ba/b 的最小值,最小值就是二分找到满足 mid∗(bi1)≥aimid * (b_i 1) ≥ a_imid∗(bi1)≥ai 的最小值 #include<bits/stdc.h> #define int long long #define x first #define y second using namespace std;void sol…...
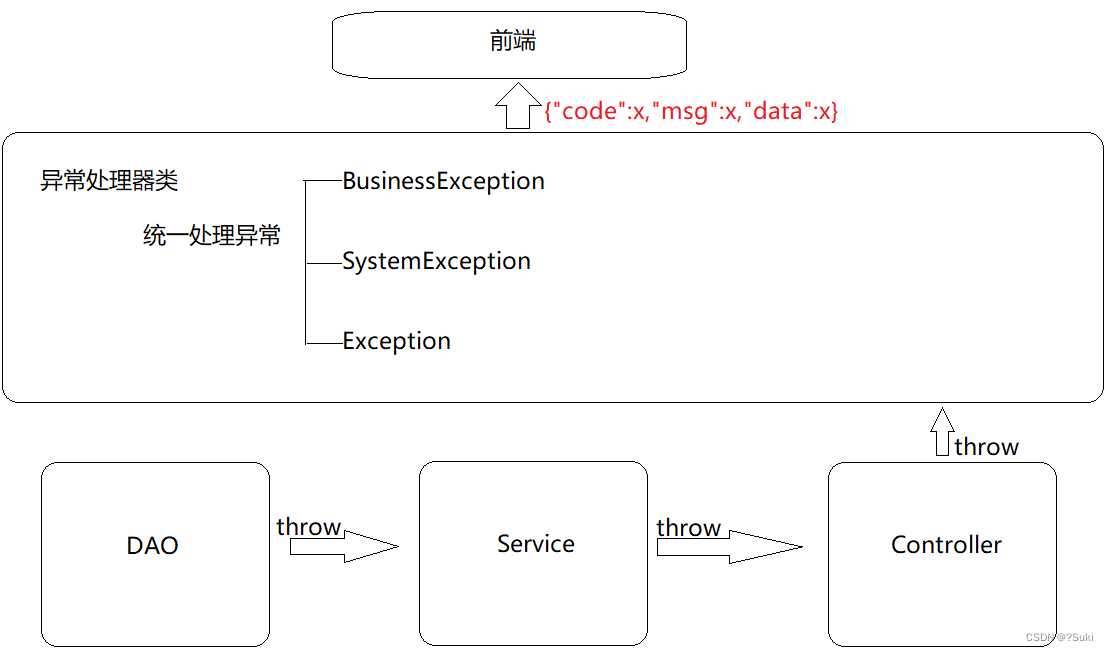
统一结果封装异常处理
统一结果封装&异常处理2,统一结果封装2.1 表现层与前端数据传输协议定义2.2 表现层与前端数据传输协议实现2.2.1 环境准备2.2.2 结果封装步骤1:创建Result类步骤2:定义返回码Code类步骤3:修改Controller类的返回值步骤4:启动服务测试3,统一异常处理3…...

数字藏品平台的发展趋势是什么?
1、数字藏品平台具体内容生产模式将在PGC(专业生产制造具体内容)方式向PUGC(技术专业用户生产内容)方式变化。 目前,中国热门的数字藏品平台都在PGC模式中持续发展的,而国外流行NFT平台则比较多选用UGC&am…...
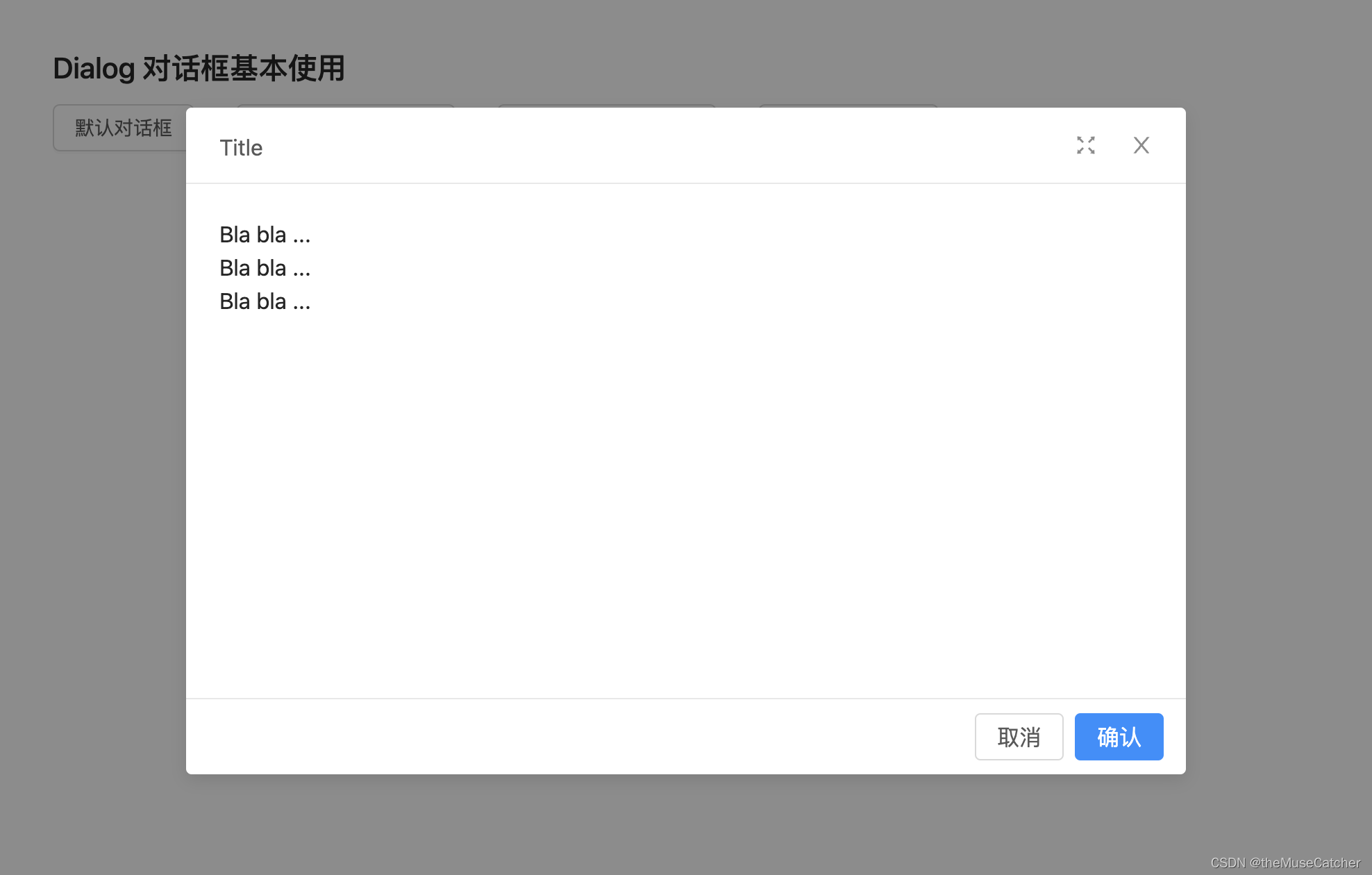
Vue3对话框(Dialog)
Vue2对话框(Dialog) 可自定义设置以下属性: 标题(title),类型:string | slot,默认 提示 内容(content),类型:string | slot…...

【深度强化学习】(5) DDPG 模型解析,附Pytorch完整代码
大家好,今天和各位分享一下深度确定性策略梯度算法 (Deterministic Policy Gradient,DDPG)。并基于 OpenAI 的 gym 环境完成一个小游戏。完整代码在我的 GitHub 中获得: https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Mod…...

unity,Color.Lerp函数
介绍 Color.Lerp函数是Unity引擎中的一个静态函数,用于在两个颜色值之间进行线性插值,从而实现颜色渐变效果 方法 Color.Lerp函数是Unity引擎中的一个静态函数,用于在两个颜色值之间进行线性插值,从而实现颜色渐变效果。该函数的…...
洛谷P8799 [蓝桥杯 2022 国 B] 齿轮 C语言/C++
[蓝桥杯 2022 国 B] 齿轮 题目描述 这天,小明在组装齿轮。 他一共有 nnn 个齿轮,第 iii 个齿轮的半径为 rir_{i}ri, 他需要把这 nnn 个齿轮按一定顺序从左到右组装起来,这样最左边的齿轮转起来之后,可以传递到最右边的齿轮&a…...

景区在线售票系统功能开发介绍
目前游客线上订票已经普及,景区开通线上购票渠道,方便游客购票,对于还没有开通线上购票的景区来说,需要提前了解一下景区线上售票系统的一些功能,下面给大家详细介绍一下景区在线售票需要哪些功能。 1、在线售票 包含门…...

webService的底层调用方式
webservice中采用协议Http,是指什么意思 WebService使用的是 SOAP (Simple Object Access Protocol)协议 Soap协议只是用来封装消息用的。封装后的消息你可以通过各种已有的协议来传输,比如http,tcp/ip,smtp,等等,你甚至还一次用自定义的协议…...
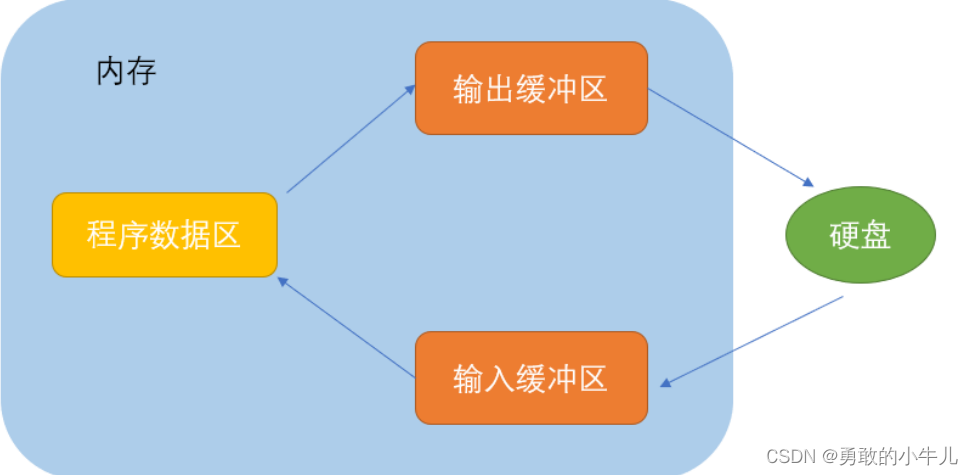
关于文件的一些小知识下
🍍个人主页🍍:🔜勇敢的小牛儿🚩 🔱推荐专栏🔱:C语言知识点 ⚠️座右铭⚠️:敢于尝试才有机会 🐒今日鸡汤🐒: 你受的苦 吃的亏 担的责 扛的罪 忍的…...

使用Cheat Engine与DnSpy破解Unity游戏
题目连接: https://play.picoctf.org/practice/challenge/361?originalEvent72&page3我们是windows系统,所以点击windows game下载游戏 双击运行pico.exe 屏幕上方的一串英文是叫我们找flag,我在这个小地图里走来走去也没flagÿ…...
溯源取证-内存取证基础篇
使用工具: volatility_2.6_lin64_standalone 镜像文件: CYBERDEF-567078-20230213-171333.raw 使用环境: kali linux 2022.02 我们只有一个RAW映像文件,如何从该映像文件中提取出我们想要的东西呢? 1.Which volatili…...
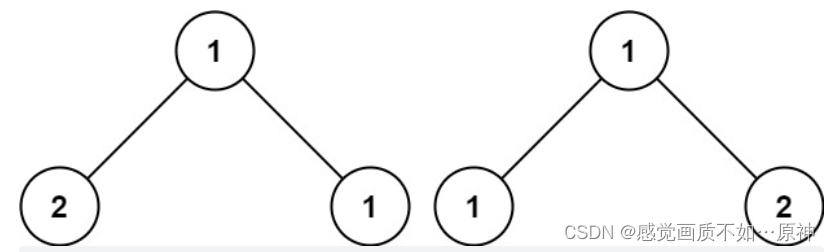
Leetcode.100 相同的树
题目链接 Leetcode.100 相同的树 easy 题目描述 给你两棵二叉树的根节点 p和 q,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 示例 1: 输入:p [1,2,3…...

每个程序员都应该知道的8大算法
在编程开发中,算法是用于解决特定问题或完成特定任务的一组指令或过程。算法可以用任何编程语言表示,可以像一系列基本操作一样简单,也可以像涉及不同数据结构和逻辑的多步骤过程一样复杂。 算法的主要目标是接收输入、处理它并提供预期的输…...
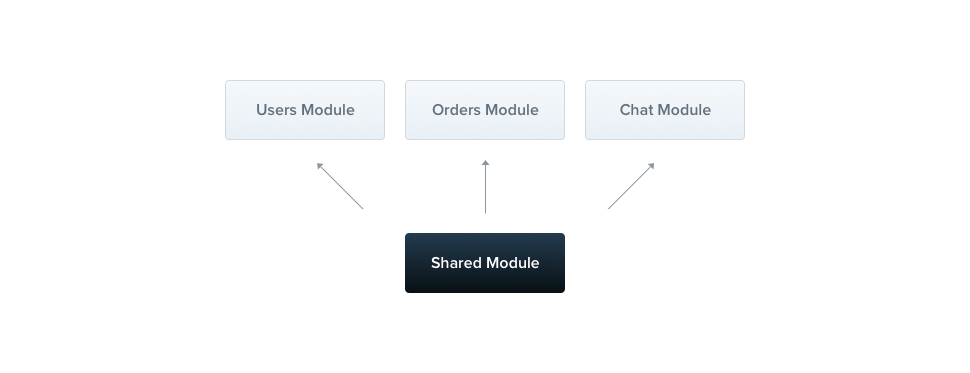
Nestjs实战超干货-概况-模块-Modules
模块 模块就是一个声明了装饰器Module()的类。装饰器Module()提供了元数据,以便让Nest组织应用程序结构。 每个应用程序至少有一个模块,即根模块。根模块是 Nest 用来构建应用程序图的起点,应用程序图是 Nest 用来解析模块和提供者关系和依赖…...

template
模板 模板注意事项 模板的函数体和声明一定要在一起,即放在同一个.h文件中,而不能将其分开到cpp和h文件中模板的编译技巧就是尽量多编译,模板很难查找错误模板的报错一般只有第一行有作用模板指定类型从左到右依次指定 模板推导 #pragma #…...
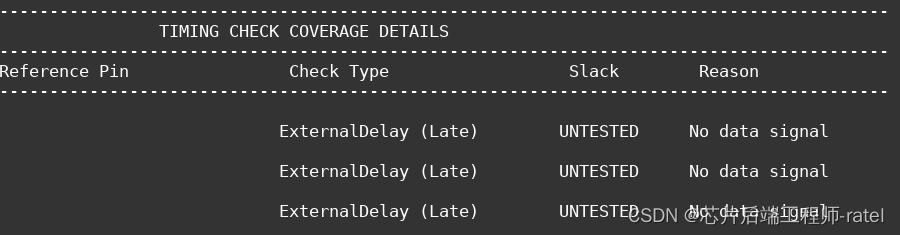
innovus中时序路径debug及命令使用详解?
写在前面:发现place结果所有与outport相关的timing check都找不到? 刚开始怀疑是sdc约束问题,check了input sdc文件及enc.dat/mmmc/mode/func.sdc 看一下是否设置了set_false_path.当然也可以用命令报出来: report_timing -unconstrained …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
