探索LeetCode【0005】最长回文子串(未搞懂,未练习)
目录
- 0、题目
- 1、第一个官方答案
- 1.1 动态规划(未懂)
- 1.2 中心扩展(已懂)
- 1.3 Manacher(未懂)
- 2、第二个参考答案
- 2.1 暴力求法(已懂)
- 2.2 反转法(未懂)
- 2.3 动态规划(未懂)
- 2.4 中心扩展(已懂)
0、题目
题目链接:【0005】最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
提示:
- 1 <= s.length <= 1000
s仅由数字和英文字母组成
1、第一个官方答案
链接
视频中的暴力解法是java代码,仅供一瞥~
class Solution {
public:string longestPalindrome(string s) {int len = s.length();if (len < 2) {return s;}int maxLen = 1;int begin = 0;// s.charAt(i) 每次都会检查数组下标越界,因此先转换成字符数组,这一步非必须char[] charArray = s.toCharArray();// 枚举所有长度严格大于1的子串 charArray[i..j]for (int i = 0; i < len - 1; i++) {for (int j = i + 1; j < len; j++) {if (j - i + 1 > maxLen && validPalindromic(charArray, i, j)) {maxLen = j - i + 1;begin = i;}}}return s.substring(begin, begin + maxLen);}private:bool validPalindromic(char[] charArray, int left, int right) {while (left < right) {if (charArray[left] != charArray[right]) {return false;}left+1;right-1;}return true;}
};
1.1 动态规划(未懂)
从视频05:35开始
#include <iostream>
#include <string>
#include <vector>using namespace std;class Solution {
public:string longestPalindrome(string s) {int n = s.size();if (n < 2) {return s;}int maxLen = 1;int begin = 0;// dp[i][j] 表示 s[i..j] 是否是回文串vector<vector<int>> dp(n, vector<int>(n));// 初始化:所有长度为 1 的子串都是回文串for (int i = 0; i < n; i++) {dp[i][i] = true;}// 递推开始// 先枚举子串长度for (int L = 2; L <= n; L++) {// 枚举左边界,左边界的上限设置可以宽松一些for (int i = 0; i < n; i++) {// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得int j = L + i - 1;// 如果右边界越界,就可以退出当前循环if (j >= n) {break;}if (s[i] != s[j]) {dp[i][j] = false;} else {if (j - i < 3) {dp[i][j] = true;} else {dp[i][j] = dp[i + 1][j - 1];}}// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置if (dp[i][j] && j - i + 1 > maxLen) {maxLen = j - i + 1;begin = i;}}}return s.substr(begin, maxLen);}
};
1.2 中心扩展(已懂)
从视频01:55开始
class Solution {
public:pair<int, int> expandAroundCenter(const string& s, int left, int right) {while (left >= 0 && right < s.size() && s[left] == s[right]) {--left;++right;}return {left + 1, right - 1};}string longestPalindrome(string s) {int start = 0, end = 0;for (int i = 0; i < s.size(); ++i) {auto [left1, right1] = expandAroundCenter(s, i, i);auto [left2, right2] = expandAroundCenter(s, i, i + 1);if (right1 - left1 > end - start) {start = left1;end = right1;}if (right2 - left2 > end - start) {start = left2;end = right2;}}return s.substr(start, end - start + 1);}
};
1.3 Manacher(未懂)
class Solution {
public:int expand(const string& s, int left, int right) {while (left >= 0 && right < s.size() && s[left] == s[right]) {--left;++right;}return (right - left - 2) / 2;}string longestPalindrome(string s) {int start = 0, end = -1;string t = "#";for (char c: s) {t += c;t += '#';}t += '#';s = t;vector<int> arm_len;int right = -1, j = -1;for (int i = 0; i < s.size(); ++i) {int cur_arm_len;if (right >= i) {int i_sym = j * 2 - i;int min_arm_len = min(arm_len[i_sym], right - i);cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);} else {cur_arm_len = expand(s, i, i);}arm_len.push_back(cur_arm_len);if (i + cur_arm_len > right) {j = i;right = i + cur_arm_len;}if (cur_arm_len * 2 + 1 > end - start) {start = i - cur_arm_len;end = i + cur_arm_len;}}string ans;for (int i = start; i <= end; ++i) {if (s[i] != '#') {ans += s[i];}}return ans;}
};
2、第二个参考答案
链接
估计和前面有些重复,搞清楚后需要予以精简!
2.1 暴力求法(已懂)
class Solution {
public:string longestPalindrome(string s) {string res="";//存放结果string temp="";//存放子串for(int i=0;i<s.length();i++){for(int j=i;j<s.length();j++){temp=temp+s[j];string tem=temp;//tem存放子串反转结果std::reverse(tem.begin(),tem.end());//反转if(temp==tem)res=res.length()>temp.length()?res:temp;}temp="";}return res;}
};
2.2 反转法(未懂)
class Solution {
public:string longestPalindrome(string s) {if(s.length()==1) return s;//大小为1的字符串必为回文串string rev=s;//rev存放s反转结果string res;//存放结果std::reverse(rev.begin(),rev.end());if(rev==s) return s;int len=0;//存放回文子串的长度for(int i=0;i<s.length();i++)//查找s与rev的最长公共子串{string temp;//存放待验证子串for(int j=i;j<s.length();j++){temp=temp+s[j];if(len>=temp.length())continue;else if(rev.find(temp)!=-1)//在rev中找到temp{string q=temp;//q用来验证temp是否是回文子串std::reverse(q.begin(),q.end());if(q==temp){len=temp.length();res=temp;}}else break;}temp="";}return res;}
};
2.3 动态规划(未懂)
class Solution {
public:string longestPalindrome(string s) {int len=s.size();if(len==0||len==1)return s;int start=0;//回文串起始位置int max=1;//回文串最大长度vector<vector<int>> dp(len,vector<int>(len));//定义二维动态数组for(int i=0;i<len;i++)//初始化状态{dp[i][i]=1;if(i<len-1&&s[i]==s[i+1]){dp[i][i+1]=1;max=2;start=i;}}for(int l=3;l<=len;l++)//l表示检索的子串长度,等于3表示先检索长度为3的子串{for(int i=0;i+l-1<len;i++){int j=l+i-1;//终止字符位置if(s[i]==s[j]&&dp[i+1][j-1]==1)//状态转移{dp[i][j]=1;start=i;max=l;}}}return s.substr(start,max);//获取最长回文子串}
};
2.4 中心扩展(已懂)
class Solution {
public:string longestPalindrome(string s) {int len=s.size();if(len==0||len==1)return s;int start=0;//记录回文子串起始位置int end=0;//记录回文子串终止位置int mlen=0;//记录最大回文子串的长度for(int i=0;i<len;i++){int len1=expendaroundcenter(s,i,i);//一个元素为中心int len2=expendaroundcenter(s,i,i+1);//两个元素为中心mlen=max(max(len1,len2),mlen);if(mlen>end-start+1){start=i-(mlen-1)/2;end=i+mlen/2;}}return s.substr(start,mlen);//该函数的意思是获取从start开始长度为mlen长度的字符串}
private:int expendaroundcenter(string s,int left,int right)//计算以left和right为中心的回文串长度{int L=left;int R=right;while(L>=0 && R<s.length() && s[R]==s[L]){L--;R++;}return R-L-1;}
};
相关文章:
)
探索LeetCode【0005】最长回文子串(未搞懂,未练习)
目录0、题目1、第一个官方答案1.1 动态规划(未懂)1.2 中心扩展(已懂)1.3 Manacher(未懂)2、第二个参考答案2.1 暴力求法(已懂)2.2 反转法(未懂)2.3 动态规划&…...

使用 Docker run 命令简化容器化
使用 Docker run 命令简化容器化 Docker run 是在 Docker 容器中运行应用程序的基本命令。在开始使用 Docker 之前,了解一些重要的命令非常重要。 在本博客中,我们将解释 Docker run 命令的基本语法,并探索其一些最常见的选项,以…...
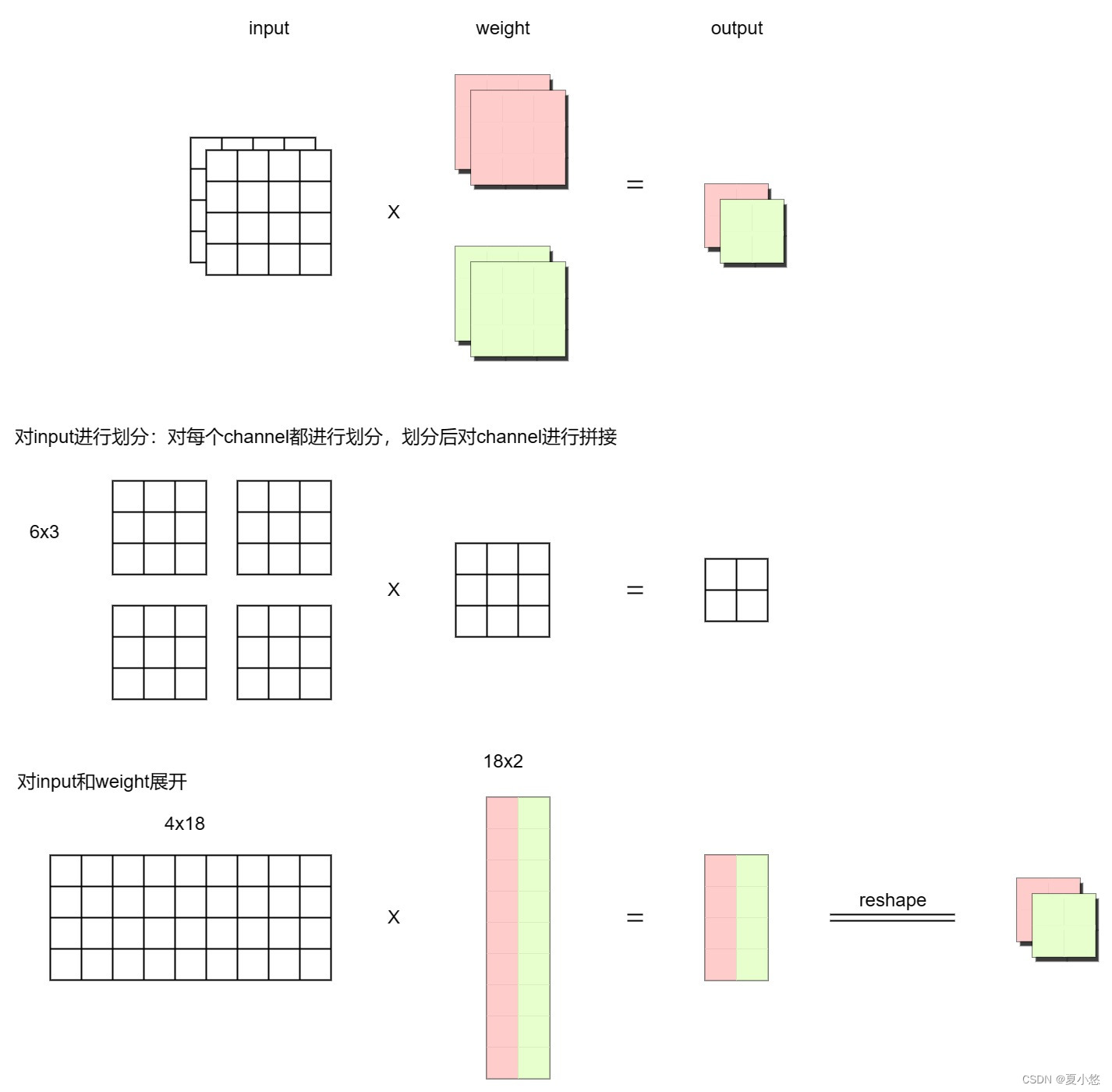
腾讯TNN神经网络推理框架手动实现多设备单算子卷积推理
文章目录前言1. 简介2. 快速开始2.1 onnx转tnn2.2 编译目标平台的 TNN 引擎2.3 使用编译好的 TNN 引擎进行推理3. 手动实现单算子卷积推理(浮点)4. 代码解析4.1 构建模型(单卷积层)4.2 构建解释器4.3 初始化tnn5. 模型量化5.1 编译量化工具5.2 量化scale的计算5.3 量化流程6. i…...

基础解惑:Linux 下文件描述符标志和文件状态标志区别
简述 文件描述符标志,是体现进程的文件描述符的状态,fork进程时,文件描述符被复制;目前只有一种文件描述符:FD_CLOEXEC文件状态标志,是体现进程打开文件的一些标志,fork时不会复制file 结构&am…...

学弟:如何在3个月内学会自动化测试?
有小学弟问:如何在3个月内学会自动化测试? 老实说如果你现在上班,之前主要在做功能测试,或者编程基础比较弱的话,三个月够呛。 如果你是脱产学习,每天能保持6~8小时学习时间的话,可…...

C-NCAP 2025主动安全ADAS测试研究
中汽中心汽车测评管理中心(简称“中汽测评”)是负责运营C-NCAP、CCRT等测评项目的管理机构。中汽测评以引领汽车行业进步、支撑汽车强国建设为使命,通过独立、公正、专业、开放的测试评价,服务消费者,当好选车购车参谋…...
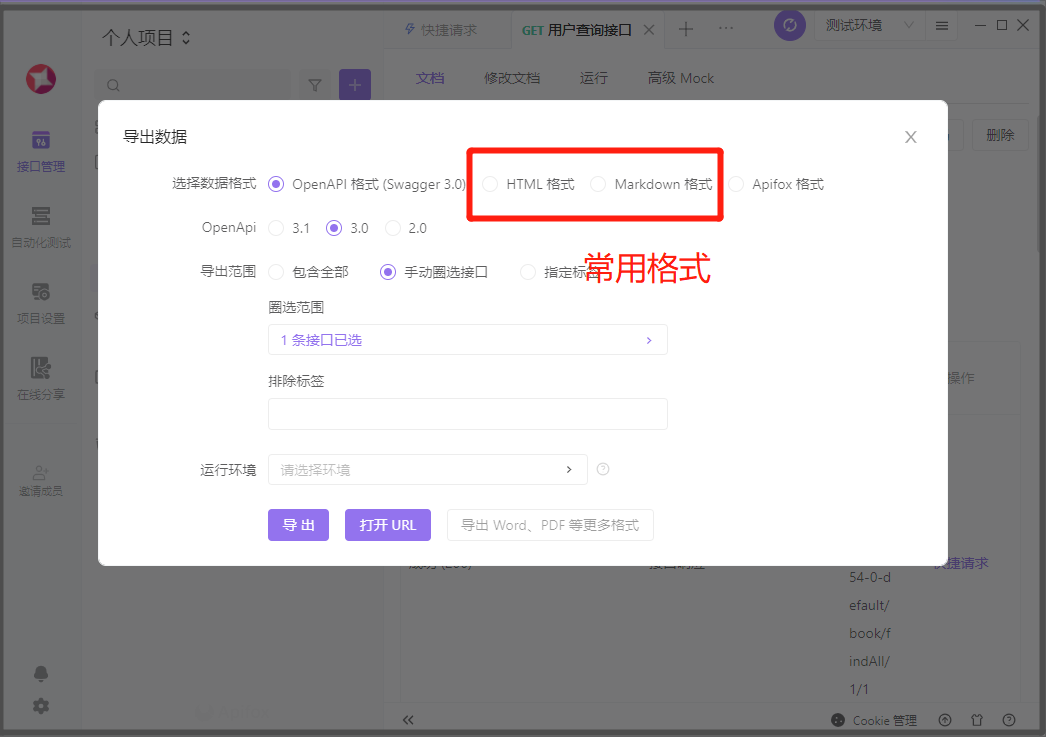
【Apifox】测试工具自动编写接口文档
在开发过程中,我们总是避免不了进行接口的测试, 而相比手动敲测试代码,使用测试工具进行测试更为便捷,高效 今天发现了一个非常好用的接口测试工具Apifox 相比于Postman,他还拥有一个非常nb的功能, 在接…...

解决brew安装opencv报错问题
目录1.报错12. 解决方案3. 报错24. 解决方案4.1 原因分析4.2 手动下载portable-ruby-2.6.8_1.el_capitan.bottle.tar.gz4.3 拷贝portable-ruby-2.6.8_1.el_capitan.bottle.tar.gz到指定目录1.报错1 mac本用brew报如下错误: xialiangzhideMacBook-Pro:~ xialz$ bre…...

Linux软件安装---Tomcat安装
安装Tomcat 操作步骤: 使用xftp上传工具将tomcat的 二进制发布包上传到Linux解压安装包,命令为tar -zxvf apache-tomcat*** -C /usr/local进入Tomcat的bin的启动目录,命令为sh startup.sh或者./startup.sh 验证Tomcat启动是否成功࿰…...

提示工程师是什么工作?
提示工程师是什么工作? 因为ChatGPT的爆火,大家都把眼光锁定在这个号称“ChatGPT新兴职业” 的“提示工程师”上。“提示工程师”是什么工作?为什么说未来所有职业 都需要提示工程的能力? 先解释一下“提示”,它最早…...

WXSS-WXML-WXS语法
目录: 1 WXSS编写程序样式 2 Mustache语法绑定 3 WXML的条件渲染 4 WXML的列表渲染 5 WXS语法基本使用 6 WXS语法案例练习 小程序的自适应单位rpx。在设计稿为iPhone6的时候1px2rpx wxml必须是闭合标签,或者单标签加/,否则会报错&#…...
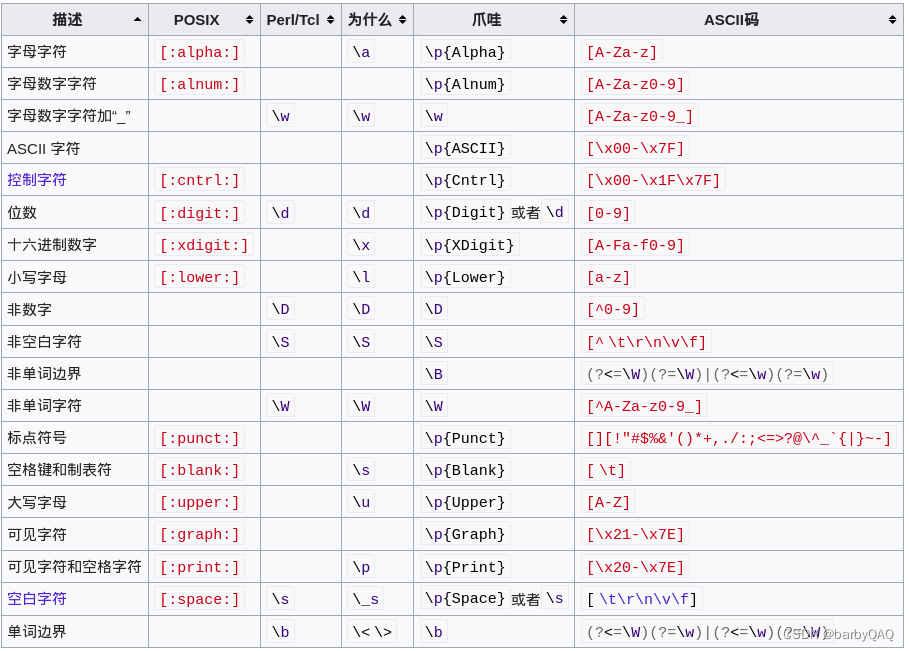
POSIX正则表达式
维基百科 POSIX基本表达式 https://en.wikibooks.org/wiki/Regular_Expressions/POSIX_Basic_Regular_Expressions POSIX扩展正则表达式 https://en.wikibooks.org/wiki/Regular_Expressions/POSIX-Extended_Regular_Expressions 正则表达式 https://en.wikipedia.org/wiki/R…...

数据分析工具集合:Tableau入门及其他工具简介
目录 一、Tableau简介 1、下载链接 2、使用技巧 二、其他常用数据分析工具 1、Microsoft Excel简介 1.1、下载链接 1.2、使用技巧 2、Python简介 2.1、下载链接 2.2、常用库的安装方式和使用技巧 2.2.1、Pandas 2.2.2、NumPy 2.2.3、Matplotlib 3、R语言简介 3.…...

响应式布局的五种方法
响应式布局的五种方法1.百分比布局2.rem布局3. 媒体查询 media screen4. flex布局5.vw 和 vh响应式布局是同一页面在不同的屏幕上有不同的布局,即只需要一套代码使页面适应不同的屏幕。 1.百分比布局 1.有父元素就相对于父元素 2.没有父元素就相对于视口的大小 举一…...

Javase学习文档------数组
Java 数组是 Java 编程中非常基础和重要的一个知识点。 以下是 Java 数组的主要学习内容: 数组的几个特点 数组在声明时必须指定长度,且长度不可变:数组的长度在声明时就需要确定,一旦确定就不能修改。因此,在使用数组…...

百度高德地图JS-API学习手记:地图基本设置与省市区数据加载
无论是百度还是高德地图开发,还是高德地图开发。官方的给的案例启示很多,copy再修改下,就完成了 概述-地图 JS API | 高德地图API 地图 JS API | 百度地图API SDK 这个大致看一下,我想。有点GIS基础都能完成地图开发。 个人认…...

c语言—指针详解***内存地址***指针字节数***注意事项
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...

VMware虚拟机之WindowsXP系统超详细下载安装与使用教程
文章目录前言一、WindowsXP虚拟机系统下载二、WindowsXP虚拟机系统安装三、WindowsXP虚拟机系统使用总结前言 本博客的主要内容为使用VMware虚拟机下载安装与使用WindowsXP系统,WindowsXP系统虽然早已过时,但是仍对我们的学习有着很大的帮助,…...

【VMD-SSA-LSSVM】基于变分模态分解与麻雀优化Lssvm的负荷预测【多变量】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

积极心态,助力人生成功
无论生活中遇到多少困难和挫折,只要我们保持积极心态、努力拼搏,就有望最终实现自己的梦想和目标。...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
