算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集
0-1背包理论
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
在下面的讲解中,我举一个例子:
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
二维dp数组
- 确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
看下面这个图:

- 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由
dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。) - 放物品i:由
dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]]为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i](物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0;
在看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
此时dp数组初始化情况如图所示:

- 确定遍历顺序
在如下图中,可以看出,有两个遍历的维度
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
要理解递归的本质和递推的方向。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:

再来看看先遍历背包,再遍历物品呢,如图:

大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!
- 举例推导dp数组
来看一下对应的dp数组的数值,如图:

class Main {public static void main(String[] args) {int[] weight = {1,3,4};int[] value = {15,20,30};int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){// 创建dp数组int goods = weight.length; // 获取物品的数量int[][] dp = new int[goods][bagSize + 1];// 初始化dp数组// 创建数组后,其中默认的值就是0for (int j = weight[0]; j <= bagSize; j++) {dp[0][j] = value[0];}// 填充dp数组for (int i = 1; i < weight.length; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]) {/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/dp[i][j] = dp[i-1][j];} else {/*** 当前背包的容量可以放下物品i* 那么此时分两种情况:* 1、不放物品i* 2、放物品i* 比较这两种情况下,哪种背包中物品的最大价值最大*/dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);}}}// 打印dp数组for (int i = 0; i < goods; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}}
}
一维dp数组
对于背包问题其实状态都是可以压缩的。
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
- 确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
- 一维dp数组的递推公式
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 + 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
- 一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
- 一维dp数组遍历顺序
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
- 举例推导dp数组
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:

public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWight = 4;testWeightBagProblem(weight, value, bagWight);}public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++){for (int j = bagWeight; j >= weight[i]; j--){dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}//打印dp数组for (int j = 0; j <= bagWeight; j++){System.out.print(dp[j] + " ");}}
分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
以上分析完,我们就可以套用01背包,来解决这个问题了。
-
确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
-
确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
-
dp数组如何初始化
在01背包,一维dp如何初始化,已经讲过,
从dp[j]的定义来看,首先dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
-
确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
-
举例推导dp数组
dp[j]的数值一定是小于等于j的。
如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
用例1,输入[1,5,11,5] 为例,如图:

最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
一维dp数组
class Solution {public static boolean canPartition(int[] nums) {int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}if(sum % 2 != 0) return false;int target = sum / 2;int[] dp = new int[target+1];for (int i = 0; i < nums.length; i++) {for (int j = target;j>=nums[i];j--) {if (j < nums[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}}return dp[target]==target;}
}
二维dp数组
class Solution {public boolean canPartition(int[] nums) {int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}if(sum % 2 != 0) return false;int target = sum / 2;int[][] dp = new int[nums.length][target+1];for (int j = nums[0]; j <= target; j++) {dp[0][j] = nums[0];}for (int i = 1; i < nums.length; i++) {for (int j = 1; j <= target; j++) {if (j < nums[i]) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);}}}return dp[nums.length-1][target]==target;}
}
相关文章:

算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集 0-1背包理论 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 在下面的讲解中&…...

SSM框架
1.mybatis的底层原理 本质上就是使用反射和动态代理来实现对应的映射关系 2.日志级别 3.传递参数 单个参数的传递和多个参数的传递 Emp selectOne(Param(“xingming”) String name); List selectByCondition(Param(“name”) String name,Param(“sal”) double sal); 4.#和…...

教育行业需要什么样的客服系统?
某教育公司拥有素质教育、成人教育、智慧教育等多个业务板块,日常通过电商、线上媒体、线上线下授课等方式进行业务开展和品牌宣传,取得了非常不错的成绩,受到了很多人的好评反馈。 对于这样一个教育公司,客户来源广泛࿰…...

花房集团任命新首席财务官:已跌破IPO发行价,活跃用户下滑
上市刚满2个月,花椒母公司花房集团(HK:03611)的高管就发生了变更。2023年2月12日,花房集团披露的公告显示,董事会宣布赵磊为该公司首席财务官(CFO),自2023年2月10日起生效。 据贝多…...

儿童绘本馆图书借阅租赁知识付费小程序源码交流
1.分类图书 2.书单推荐 4.会员卡次、期限购买 5.借阅时间选择 6.积分签到 7.优惠Q领取 前端uniapp开发 后端thinkphp开发 完全开源 <template> <view class"sp-section sp-index"> <!-- search --> <view class&qu…...

Vue3 中 axios 的安装及使用
目录前言:一、什么是 axios ?二、Axios 的配置项三、Axios 的请求方式四、自定义创建实例五、Axios 请求错误处理六、Axios 解决跨域问题七、Axios 请求案例随机笑话大全总结:前言: 在编写vue里的项目时,必须要用和后台…...

Django设计模式以及模板层介绍
MVC和MTV 传统的MVC作用:降低模块间的耦合度(解耦)Django的MTV模式 作用:降低模块间的耦合度(解耦)什么是模板 1、模板是可以根据字典数据动态变化的html网页2、模板可以根据视图中传递的字典数据动态生成相…...

Linux信号一门搞定
1.信号是什么? 信号其实就是一个软件中断。 例: 输入命令,在Shell下启动一个前台进程。用户按下Ctrl-C,键盘输入产生一个硬件中断。如果CPU当前正在执行这个进程的代码,则该进程的用户空间代码暂停执行,…...

手撸一个动态Feign,实现一个“万能”接口调用
Feign,在微服务框架中,是的服务直接的调用变得很简洁、简单,而不需要再编写Java Http调用其他微服务的接口。 动态feign 对于fegin调用,我们一般的用法:为每个微服务都创建对应的feignclient接口,然后为每…...
Linux Capabilities 入门
目录 Linux capabilities 是什么? capabilities 的赋予和继承 线程的 capabilities Permitted Effective Inheritable Bounding Ambient 文件的 capabilities Permitted Inheritable Effective 运行 execve() 后 capabilities 的变化 案例 Linux capab…...

驱动 day6
关于设备树的理解: 设备树(Device Tree)是一种用于特定硬件设备的解释语法树。它用来表示存储有关主板硬件和CPU架构信息的数据在内核中的传递格式,使内核可以更好地了解硬件并支持它们,而不必编写固定的代码。设备节点…...
附录2-tensorflow目标检测
源码来自作者Bubbliiiing,我对参考链接的代码略有修改,网盘地址 链接:百度网盘 请输入提取码 提取码:dvb1 目录 1 参考链接 2 环境 3 数据集准备 3.1 VOCdevkit/VOC2007 3.2 model_data/voc_classes.txt 3.3 voc_an…...

常见的EMC问题
电磁兼容设计的目的就在于满足产品功能要求、减少调试时间,使产品满足电磁兼容标准的要求,并且使产品不会对系统中的其它设备产生电磁干扰。 电磁兼容设计中常见的问题有哪些? 1、电磁兼容设计可以从电路设计(包括器件选择&…...

Redis内存存储效率问题
目录 内存碎片是如何形成的? 如何判断是否有内存碎片? 如何清理内存碎片? INFO命令 面向 Prometheus 的 Redis-exporter 监控 实习期间,了解到,企业级开发中多个项目使用Redis,运行Redis实例的有可能是…...
3.28 haas506 2.0开发教程-example-蓝牙多设备扫描(仅支持M320,HD1)
haas506 2.0开发教程-example-蓝牙多设备扫描案例说明蓝牙信息克隆1.手机蓝牙改名信息克隆代码测试案例说明 开发板扫描蓝牙设备,获取并打印蓝牙设备mac地址。mac地址每个设备不同,且不能更改。本案例仅适用于M320开发板和HD1-RTU。案例使用手机与iBeac…...
C语言经典编程题100例(41~60)
目录41、习题4-4 特殊a串数列求和42、习题4-6 水仙花数43、习题4-7 最大公约数和最小公倍数44、习题7-5 找鞍点45、练习5-1 求m到n之和46、练习5-2 找两个数中最大者47、练习5-3 数字金字塔48、习题5-1 符号函数49、习题5-2 使用函数求奇数和50、习题5-3 使用函数计算两点间的距…...
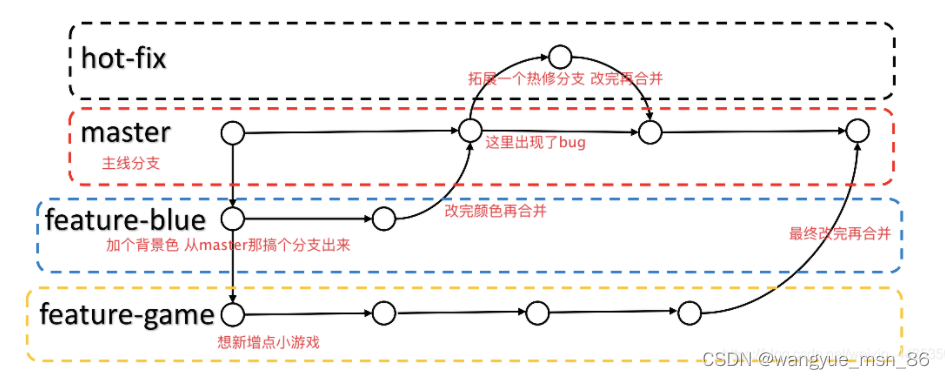
git日常使用命令
实习这段时间使用了很多git指令来提交代码,简单记录一下日常使用的指令: 提交代码通常顺序: 1.git status 查看本地修改项 2.git add . 提交全部文件 (这个 .是全部文件)到暂存区 3.git commit -m ‘本次提交的说明’…...

ES6对象展开运算符浅拷贝or深拷贝
ES6中提出的对象展开运算符“…”就是用来展开元素的。有了它就不用代码循环遍历了,偷懒专用。 1. 合并数组 展开原有数组中的所有元素,可以合并成一个新的数组。 var a[1,2,3]; var b[4,5,6]; var c[...a,...b]; console.log(c) // 输出:…...

leaflet 上传包含shp的zip文件,在map上解析显示图形(059)
第059个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中本地上传包含shp的zip文件,利用shapefile读取shp数据,并在地图上显示图形。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果 文章目录 示例效果加载shapefile.js方式安装引用jszip(…...
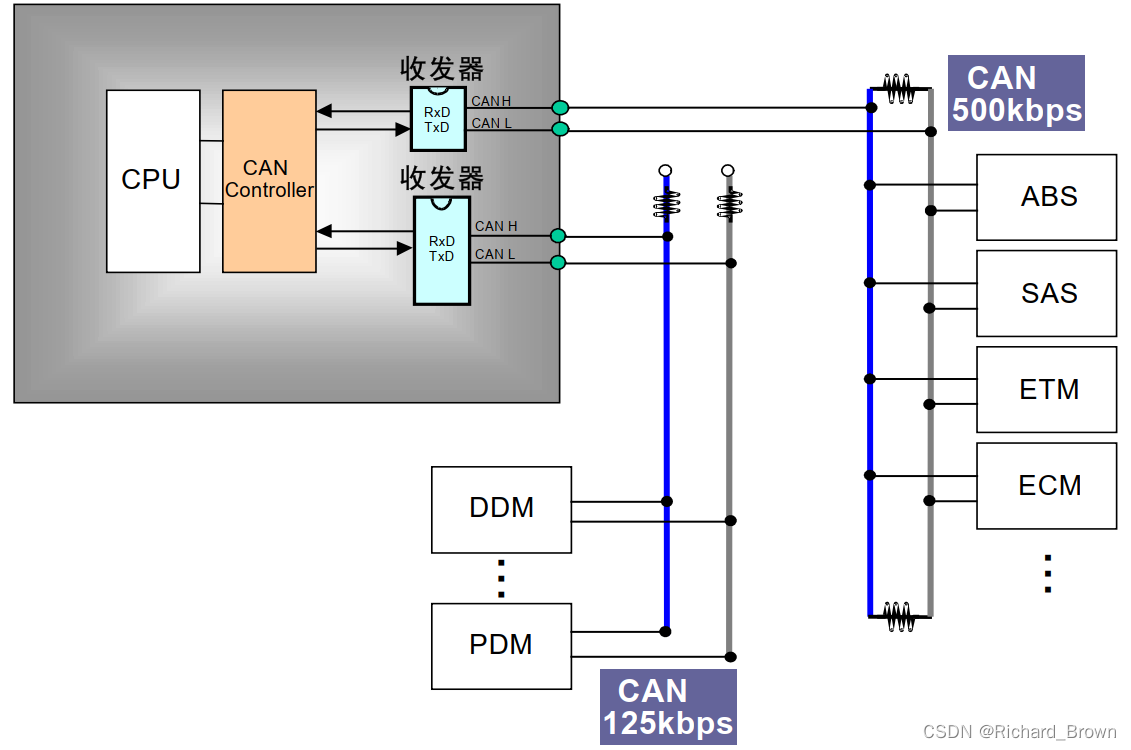
CAN总线详细介绍
1.1 CAN是什么? CAN 最终成为国际标准 ( ISO11898(高速应用)和 ISO11519(低速应用)),是国际上应用最广泛的现场总线之一。 1.2 CAN总线特点 多主方式: 可以多主方式工作,网络上任意一个节点…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
