机器学习中的数学原理——过拟合、正则化与惩罚函数
通过这篇博客,你将清晰的明白什么是过拟合、正则化、惩罚函数。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一下我在 机器学习中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言!这一篇就更新一下《 白话机器学习中的数学——过拟合、正则化与惩罚函数》
文章目录
- 一、过拟合
- 二、正则化
- 2.1 正则化的方法
- 2.2 正则化的效果
- 三、惩罚函数
一、过拟合
之前我们提到过的模型只能拟合训练数据的状态被称为过拟合,英文是 overfitting。记得在学习回归的时候,过度增加函数 fθ(x)的次数会导致过拟合。过拟合不止在回归时出现,在分类时也经常发生,我们要时常留意它。
避免过拟合有以下方法:
- 增加全部训练数据的数量
- 使用简单的模型
- 正则化
首先,重要的是增加全部训练数据的数量。之前我也讲过,机器学习是从数据中学习的,所以数据最重要。另外,使用更简单的模型也有助于防止过拟合。
二、正则化
2.1 正则化的方法
还记得我们在讲解回归的时候提到的目标函数吗?
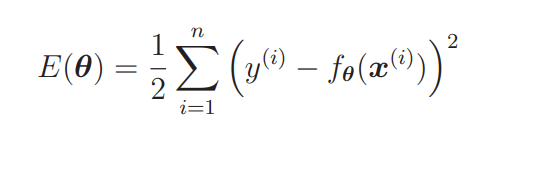
我们要向这个目标函数增加下面这样的正则化项:
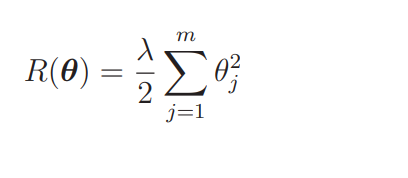
那么现在的E(θ)E(\boldsymbol{\theta})E(θ)就变为:
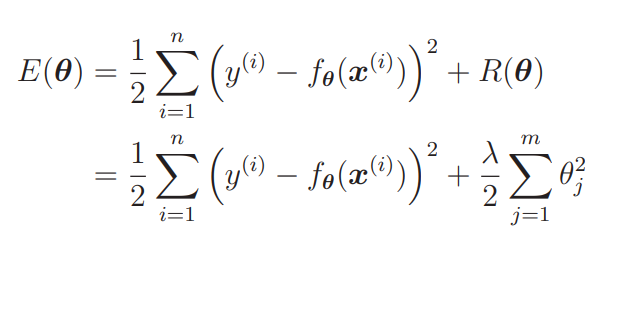
我们要对这个新的目标函数进行最小化,这种方法就称为正则化。
m 是参数的个数,不过一般来说不对 θ0 应用正则化。所以仔细看会发现 j 的取值是从 1 开始的。也就是说,假如预测函数的表达式为 fθ(x) = θ0 + θ1x + θ2x2,那么 m = 2 就意味着正则化的对象参数为 θ1 和 θ2,θ0 这种只有参数的项称为偏置项,一般不对它进行正则化。λ 是决定正则化项影响程度的正的常数。这个值需要我们自己来定。
2.2 正则化的效果
光看表达式可能不容易理解。我们结合图来想象一下吧:首先把目标函数分成两个部分。
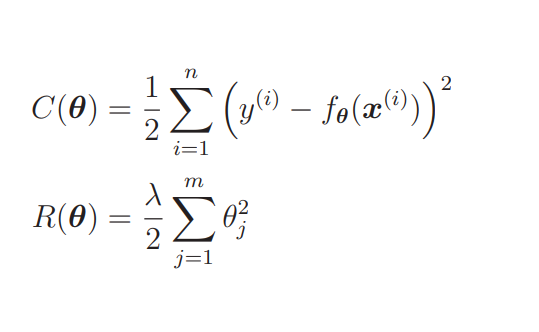
C(θ) 是本来就有的目标函数项,R(θ) 是正则化项。 C(θ) 和 R(θ) 相加之后就是新的目标函数,所以我们实际地把这两个函数的图形画出来,加起来看看。不过参数太多就画不出图来了,所以这里我们只关注 θ1。而且为了更加易懂,先不考虑 λ。
我们先从C(θ) 开始画起,不用太在意形状是否精确。在讲回归的时候,我们说过这个目
标函数开口向上,还记得吗?所以,我们假设它的形状是这样的:
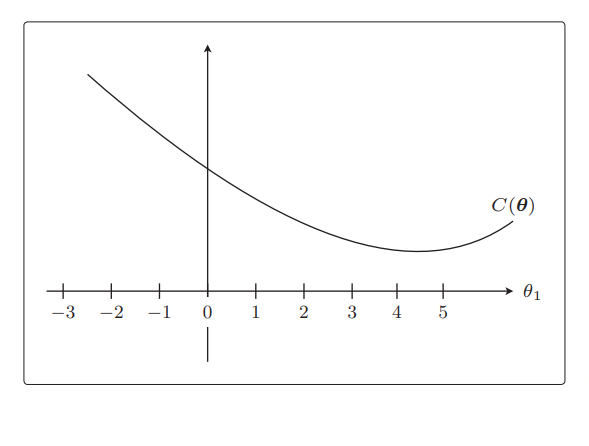
从图中马上就可以看出最小值在哪里,是在θ1 = 4.5 附近。
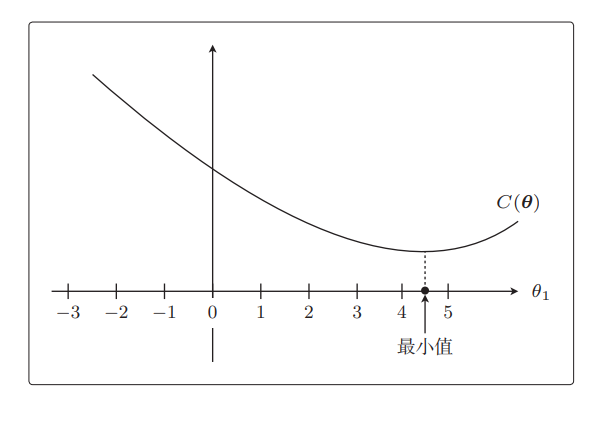
从这个目标函数在没有正则化项时的形状来看,θ1 = 4.5 附近是最小值。接下来是 R(θ),它就相当于12θ12\frac{1}{2} \theta_1^221θ12所以是过原点的简单二次函数。
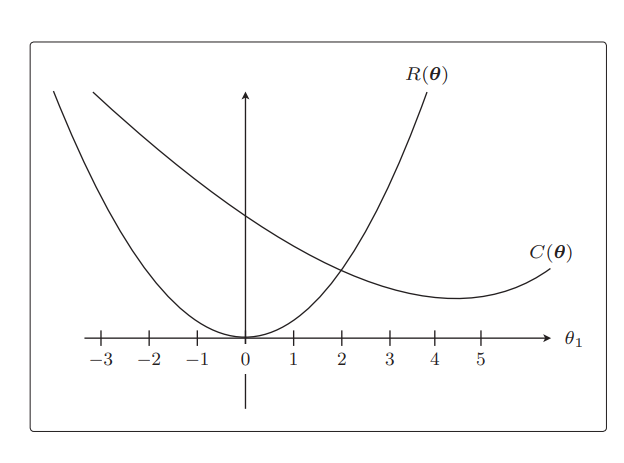
实际的目标函数是这两个函数之和E(θ) = C(θ) + R(θ),我们来画一下它的图形。顺便考虑一下最小值在哪里。把 θ1 各点上的 C(θ) 和 R(θ) 的高相加,然后用线把它们相连就好:
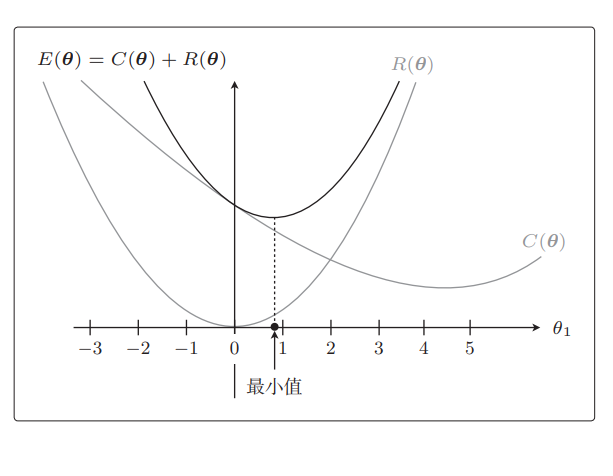
从图中我们可以看出来最小值是 θ1 = 0.9,与加正则化项之前相比,θ1 更接近 0 了。本来是在 θ1 = 4.5 处最小,现在是在 θ1 = 0.9 处最小,的确更接近 0 了。这就是正则化的效果。它可以防止参数变得过大,有助于参数接近较小的值。虽然我们只考虑了 θ1,但其他 θj 参数的情况也是类似的。
参数的值变小,意味着该参数的影响也会相应地变小。比如,有这样的一个预测函数 fθ(x):fθ(x)=θ0+θ1x+θ2x2f_{\boldsymbol{\theta}}(\boldsymbol{x})=\theta_0+\theta_1 x+\theta_2 x^2 fθ(x)=θ0+θ1x+θ2x2
极端一点,假设 θ2 = 0,这个表达式就从二次变为一次了,这就意味着本来是曲线的预测函数变为直线了:
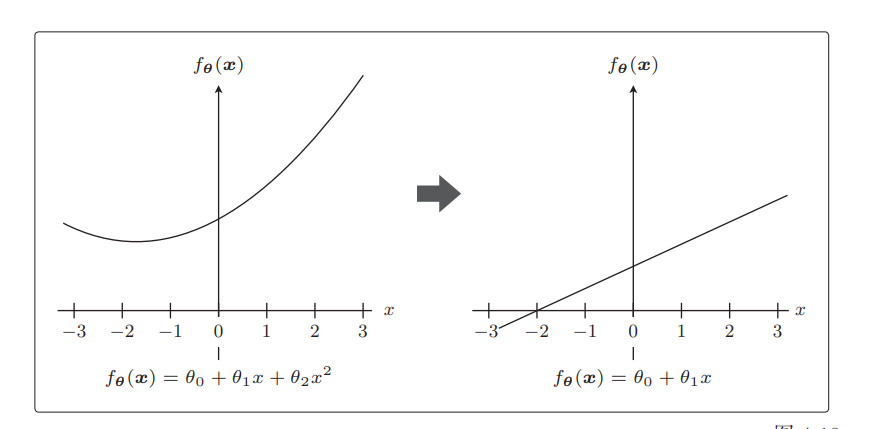
这正是通过减小不需要的参数的影响,将复杂模型替换为简单模型来防止过拟合的方式。
三、惩罚函数
为了防止参数的影响过大,在训练时要对参数施加一些惩罚。比如上面提到的 λ,可以控制正则化惩罚的强度。C(θ)=12∑i=1n(y(i)−fθ(x(i)))2R(θ)=λ2∑j=1mθj2\begin{aligned} & C(\boldsymbol{\theta})=\frac{1}{2} \sum_{i=1}^n\left(y^{(i)}-f_{\boldsymbol{\theta}}\left(\boldsymbol{x}^{(i)}\right)\right)^2 \\ & R(\boldsymbol{\theta})=\frac{\lambda}{2} \sum_{j=1}^m \theta_j^2 \end{aligned} C(θ)=21i=1∑n(y(i)−fθ(x(i)))2R(θ)=2λj=1∑mθj2
比如令 λ = 0,那就相当于不使用正则化
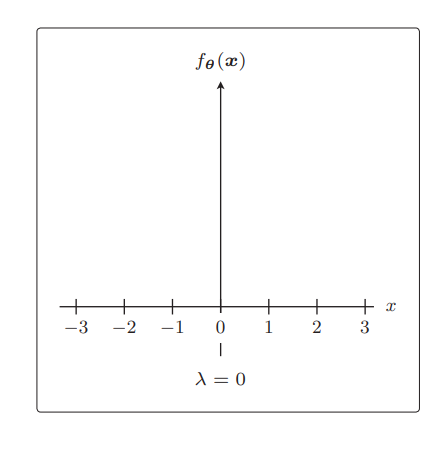
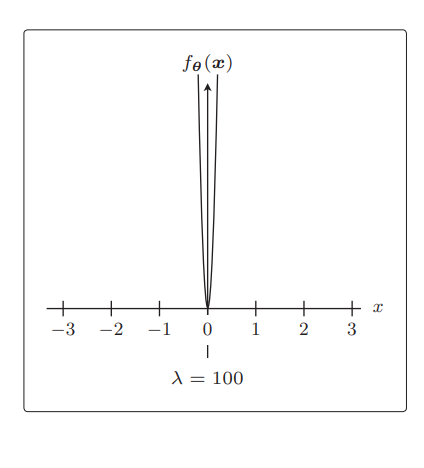
λ 越大,正则化的惩罚也就越严厉:
相关文章:

机器学习中的数学原理——过拟合、正则化与惩罚函数
通过这篇博客,你将清晰的明白什么是过拟合、正则化、惩罚函数。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一下我在 机器学习中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言…...

RK3588S imx415摄像头调试
一、环境 soc:rk3588sensor:imx415board: AIO-3588SJDlinux:rk3588_linux_release_20230301_v1.0.6e 二、imx415简介 品牌:SONY型号:IMX415接口:MIPI CSI 三、驱动移植 瑞芯微支持的摄像头,有…...

「SAP ABAP」OPEN SQL(七)【GROUP BY | HAVING | ORDER BY】
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后端的开发语言A…...

容器-LinkedList
LinkedList LinkedList的概述 LinkedList的底层使用双向链表实现。 链表是一种线性数据结构,其中每个元素都是一个单独的对象,包含一个指向列表中下一个节点的引用。 它可以用于实现各种抽象数据类型,例如列表、堆栈、队列等。 LinkedLis…...

Flask 路由和视图函数
Flask 路由和视图函数一、路由 (Routing)二、视图函数 (View Functions)三、动态路由四、HTTP方法五、总结在Flask中,路由和视图函数是两个核心概念,它们协同工作以处理用户请求并生成响应。一、路由 (Routing) 路由是URL到Python函数的映射。当用户访问…...
Linux主机 SSH 通过密钥登录
我们一般使用 PuTTY 等 SSH 客户端来远程管理 Linux 服务器。但是,一般的密码方式登录,容易有密码被暴力破解的问题。所以,一般我们会将 SSH 的端口设置为默认的 22 以外的端口,或者禁用 root 账户登录。其实,有一个更…...

中国信息安全测评中心-自主原创测评
信息技术产品自主原创测评是适应我国经济社会发展的需要,是适应国际知识产权保护的发展趋势,鼓励信息技术产业的自主创新和维护权利人合法权益的重要举措。 信息技术产品自主原创测评业务是指在开发者自主声明的基础上,通过对关键技术实现的全…...

redis杂谈之部分重同步的实现
背景: 部分重同步则用于处理断线后重复制情况:当从服务器在断线 后重新连接主服务器时,如果条件允许,主服务器可以将主从服务器连 接断开期间执行的写命令发送给从服务器,从服务器只要接收并执行这 些写命令ÿ…...

多态部分参考答案
一、选择题 1、下列关于动态联编的描述中,错误的是()。 A.动态联编是以虚函数为基础 B.动态联编是运行时确定所调用的函数代码的 C.动态联编调用函数操作是指向对象的指针或对象引用 D.动态联编…...

【高项】项目人力资源管理,沟通管理与干系人管理(十大管理)
【高项】项目人力资源管理,沟通管理与干系人管理(十大管理) 文章目录1、人力资源管理1.1 什么是人力资源管理?1.2 如何进行人力资源管理?(过程)1.3 人力资源管理工具1.4 人力资源管理文件2、沟通…...

Wikijs简介-强大可扩展的开源维基软件
Wikijs - 最强大 最可扩展的开源维基软件 使用 wiki.js 美丽直观的界面,让文档成为写作的乐趣! 优点 🔧 随时随地安装 几乎适用于任何平台,并与PostgreSQL、MySQL、MariaDB、MS SQL Server 或 SQLite 兼容! ⚙️ 管…...
)
微博舆情分析系统的设计与实现(python)
背景分析 随着互联网大趋势的到来,社会的方方面面,各行各业都在考虑利用互联网作为媒介将自己的信息更及时有效地推广出去,而其中最好的方式就是建立网络管理系统,并对其进行信息管理。由于现在网络的发达,微博舆情分析系统的资讯信息通过网络进行信息管理掀起了热潮,所…...

【AUTOSAR】【Lin通信】LinTrcv
目录 一、概述 二、功能说明 2.1 LIN收发器驱动程序操作模式 2.2 LIN收发器硬件操作模式 2.3 LIN收发器唤醒类型 2.4 LIN收发器唤醒模式 2.5 错误分类 2.5.1 开发错误 三、API接口 3.1 API定义 一、概述 该规范规定了模块LIN收发器驱动程序的功能、API和配置。它负责…...
UE4C++学习篇(十九)-- 动画蒙太奇初级使用
用一个第三人称的射击案例来简单介绍一下动画蒙太奇的使用,动画蒙太奇的具体介绍这里就不多说了,不知道的小伙伴可以去搜一下了解。 这里介绍角色射击,射击的时候播放一个射击动画。 选中需要创建出动画蒙太奇的动画,点击创建&am…...

子集和问题
目录 子集和问题 程序设计 程序分析 子集和问题 【问题描述】子集和问题的一个实例为〈S,c〉。其中,S={ x1 , x2 ,…,xn }是一个正整数的集合,c是一个正整数。子集和问题判定是否存在S的一个子集S1,使得: 试设计一个解子集和问题的回溯法。 对于给定的正整数的集…...

苹果蓝牙耳机太贵了买哪个替代?苹果蓝牙耳机平替推荐
随着人们生活水平的提高,蓝牙耳机已经遍布在我们生活的各个角落。同时随着科技的发展,许多人果粉选择苹果耳机平替。下面我们一起来看看2023年有哪些适用于苹果的平替蓝牙耳机吧! 一、南卡小音舱Lite2蓝牙耳机 蓝牙版本:5.3 售…...

CK-UR05-US桌面式超高频RFID发卡器开发手册之USB控制命令格式
CK-UR05-US桌面式超高频RFID发卡器支持USB控制命令格式,本文重点就此格式展开说明! CK-UR05-US桌面式超高频RFID发卡器1、取版本号(GetReaderVersion) 功能:取读写器的硬件、软件版本 命令码: 02H 命令参数:无 命令包: 『40H 02H 02H BCH』 举例: 如…...

【华为OD机试】1025 - 字符串加解密
文章目录一、题目🔸题目描述🔸输入输出🔸样例1二、代码参考作者:KJ.JK🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 &#x…...

阿里云版GPT官宣,我们问了它10个问题
4月7日,阿里云宣布自研大模型“通义千问”,目前已开始邀请用户测试体验。 阿里达摩院在NLP自然语言处理等前沿科研领域早已布局多年,并于2019年启动大模型研发,通义千问便是其最新成果,相当于阿里云版的“ChatGPT”。 …...

ORM框架之NHibernate
什么是NHibernate NHibernate是一个开源的对象关系映射(ORM)框架,它允许开发人员使用面向对象的方式来访问关系型数据库。它是Hibernate框架的C#版本,Hibernate框架是Java平台上的ORM框架。 使用NHibernate,您可以将…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
