feign技巧 - form方式传值
feign技巧 - form方式传值。
0. 文章目录
- 1. 前言
- 2. 调用样例
- 3. 原理解析
- 3.1 feign端序列化参数
- 3.2 SpringMVC服务端解析参数
- 3.3 补充 - 继承关系不会被传递的原因
- 3.4 补充 - 不能使用GET。
- 4. 总结
1. 前言
直接正题。 如何使用feign进行fom表单方式的请求调用,以及其中的注意事项。
2. 调用样例
// =============================================== feign调用端// 注意事项:// 1. 两个参数都要使用@RequestPart注解进行标注.// 2. consumes属性配置为必选.// 3. 代表参数载体对象的params字段, 不能存在继承关系, 所有字段都必须直接定义在KDeployParams中. 如果存在基类, 那么处理流程中,只有在`KDeployParams`中直接定义的字段才能被正确解析并传递给服务端,基类的字段不会被feign解析传递. @PostMapping(value = "/projectB/postWithFormData", consumes = MediaType.MULTIPART_FORM_DATA_VALUE)String postWithFormData(@RequestPart("file") MultipartFile file, @RequestPart KDeployParams params);// =============================================== 对应的服务端 // 注意事项:// 1. 第二个参数params前面没有任何注解, 或者使用@ModelAttribute。千万不要使用@RequestPart.@PostMapping("/projectB/postWithFormData")public String postWithFormData(@RequestPart(required = false, name = "file") MultipartFile file,KDeployParams params) throws InterruptedException, IOException { ... } 3. 原理解析
分为两部分 —— 发送端的feign,以及服务端的SpringMVC。
3.1 feign端序列化参数
整条请求链路中,feign端的调用层级最终会来到位于feign-form-xx.jar中的MultipartFormContentProcessor.process (...) 。
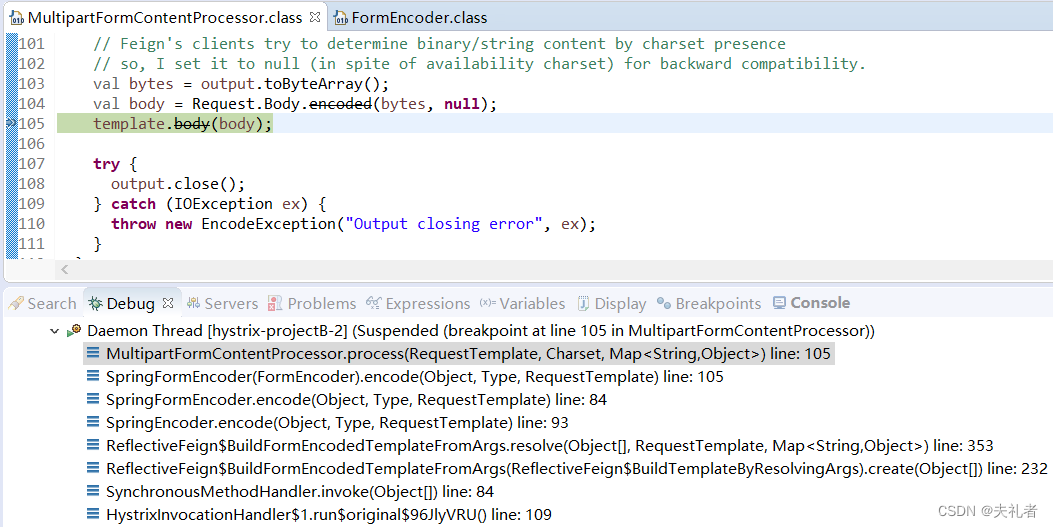
3.2 SpringMVC服务端解析参数
针对上文例子中,在服务端接收层面,SpringMVC中负责传递过来的参数还原/反序列化为KDeployParams的是ServletModelAttributeMethodProcessor(该类实现了大名鼎鼎的HandlerMethodArgumentResolver)。
3.3 补充 - 继承关系不会被传递的原因
PojoUtil的坑,下面这里只会检索出当前类直接声明的字段。
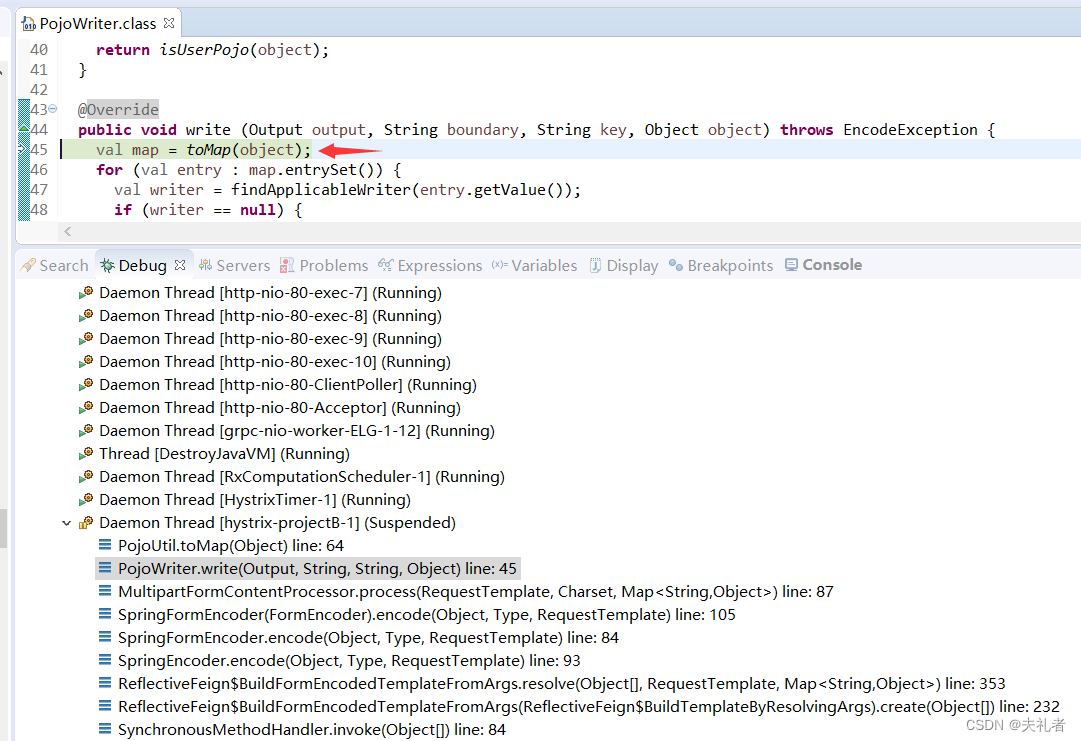
3.4 补充 - 不能使用GET。
否则报如下错误:

4. 总结
神在细节之中。
细节是魔鬼。
相关文章:

feign技巧 - form方式传值
feign技巧 - form方式传值。 0. 文章目录1. 前言2. 调用样例3. 原理解析3.1 feign端序列化参数3.2 SpringMVC服务端解析参数3.3 补充 - 继承关系不会被传递的原因3.4 补充 - 不能使用GET。4. 总结1. 前言 直接正题。 如何使用feign进行fom表单方式的请求调用,以及其…...

MATLAB | 情人节来绘制更立体的玫瑰花吧
又是一年情人节,今年带来一款更有立体感的玫瑰: 曲面的函数表达式来自: http://www.bugman123.com/Math/index.html 这个网站,上面还有很多其他帅气的玩意。 基础绘制 xlinspace(0,1,300); thetalinspace(-2*pi,15*pi,300); [x,theta]meshg…...

【Python表白代码】 2.14“Valentine‘s Day”“没别的意思 就是借着特殊日子说声喜欢你”你在哪儿?我去见你~(各种玫瑰源码合集)
导语 Valentines Day Every man is a poet when he is in love 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 哈喽!我是你们的木木子吖~ 情人节又到了,礼物备好了没&am…...

压力应变电桥信号隔离放大变送器差分输入0-±10mV/0-±20mV转0-20mA/0-10v
概述:DIN11 IPO 压力应变桥信号处理系列隔离放大器是一种将差分输入信号隔离放大、转换成按比例输出的直流信号导轨安装变送模块。产品广泛应用在电力、远程监控、仪器仪表、医疗设备、工业自控等行业。此系列模块内部嵌入了一个高效微功率的电源,向输入…...

Linux系统之部署个人导航页
Linux系统之部署个人导航页 一、本次导航页工具介绍二、检查本地系统环境1.检查系统版本2.检查系统内核版本三、下载导航页软件包1.创建下载目录2.下载导航页软件包四、部署前环境准备工作1.安装python32.安装pipenv3.创建虚拟环境①创建环境②修改base.py文件③修改settings.p…...

四、Windows 平台安装 MongoDB
MongoDB 提供 64 位系统的预编译二进制包 我们可以从 MongoDB 官网下载安装 MongoDB 预编译二进制包下载地址:Try MongoDB Atlas Products | MongoDB 在 MongoDB 2.2 版本后已经不再支持 Windows XP 系统 最新版本也已经没有了 32 位系统的安装文件 MongoDB for W…...
浅谈应用安全测试工具
正确的应用程序安全测试工具可以改善企业安全态势和开发工作流程。如今,应用程序安全从一开始就内置在整个软件生命周期中,即使是具有成熟开发实践的组织也需要自动化工具来在复杂、快速变化的环境中成功地保护他们的软件。以下比较了三个广泛使用的应用…...

四类(七种)排序算法总结
一、插入排序 基本思想: 每次将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。即边插入边排序,保证子序列中随时都是排好序的。 基本操作——有序插入ÿ…...

[oeasy]python0083_十进制数如何存入计算机_八卦纪事_BCD编码_Binary_Coded_Decimal
编码进化 回忆上次内容 上次 研究了 视频终端的 演化 从VT05 到 VT100从 黑底绿字 到 RGB 24位真彩色形成了 VT100选项 从而 将颜色 数字化 了 生活中我们更常用 10个数字 但是 计算机中 用二进制 日常计数的十进制数 是如何存储进计算机的呢?🤔 从10进制到2进…...

理解框架的编译时与运行时
首先我们需要先理解一下什么事编译时和运行时 在语言层面,先来聊一下前端开发者最常遇见的两种语言JavaScript和Java Java的代码就是被编译为.class 文件才能运行,这个编译过程就是编译时,运行 .class 文件就是运行时我们在浏览器直接输入一…...
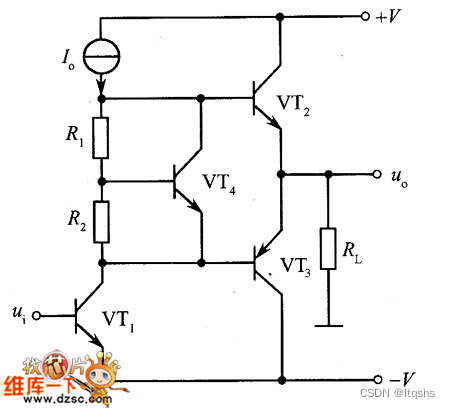
推挽电路---采用二极管消除交越失真----克服交越失真的互补推挽输出电路图
交越失真产生的原因及消除方法 由于晶体管的门限电压不为零,比如一般的硅三极管,NPN型在0.7V以上才导通,这样在00.7就存在死区,不能完全模拟出输入信号波形,PNP型小于-0.7V才导通,比如当输入的交流的正弦波…...

day11_面向对象
今日内容 零、 复习昨日 一、一日一题(数组,OOP) 二、面向对象练习(方法参数返回值) 三、局部变量&成员变量 四、this关键字 五、构造方法 六、重载 七、封装 小破站同步上课视频: https://space.bilibili.com/402601570/channel/collectiondetail?…...
大数据处理学习笔记1.1 搭建Scala开发环境
文章目录零、本讲学习目标一、Scala简介(一)Scala概述(二)函数式编程(三)Scala特性1、一切都是对象2、一切都是函数3、一切都是表达式(四)在线运行Scala二、选择Scala版本三、Window…...

VSCODE C++ 调用matplotlibcpp画图
使用VSCODE编写C程序,想在调试过程中看中间数据的波形,于是找到了python的matplotlibcpp库,参考文章链接是:https://blog.csdn.net/weixin_43769166/article/details/118365416;按照他的步骤配置好之后,跳出…...
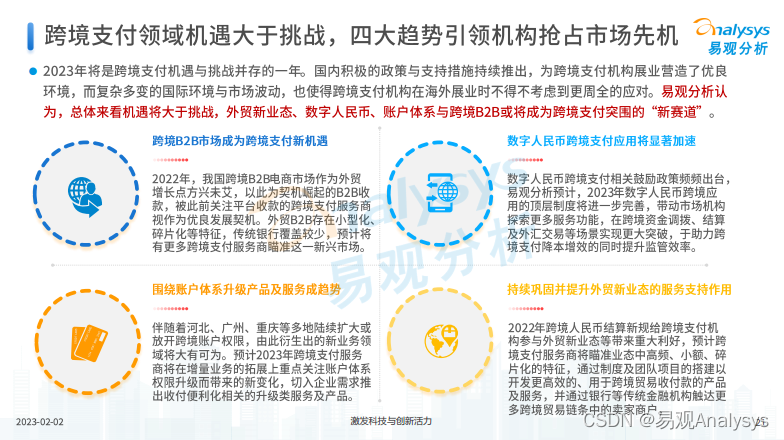
面对“开门红”,跨境支付如何寻求新增长曲线?
易观:2022年是第三方支付行业洗牌加剧的一年,在部分机构选择退出的过程中,也有机构开始瞄准跨境业务,成为了支付机构转型的重要方向之一。跨境支付是指两个或及其以上的国家或地区进行国际贸易、国际投资或其他经济活动࿰…...
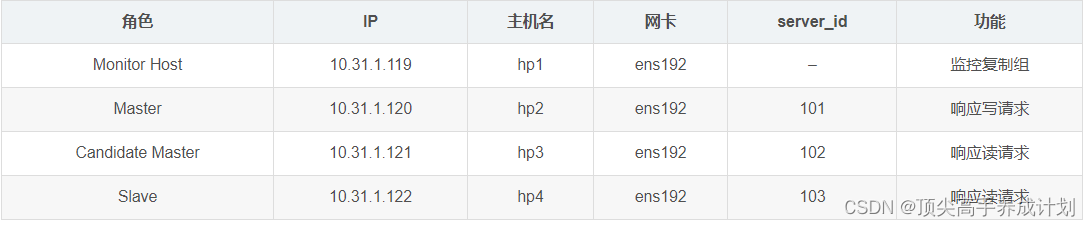
MySQL入门篇-MySQL MHA高可用实战
MHA简介 MHA(Master High Availability)目前在MySQL高可用方面是一个相对成熟的解决方案,它由日本DeNA公司的youshimaton(现就职于Facebook公司)开发,是一套优秀的作为MySQL高可用性环境下故障切换和主从提…...
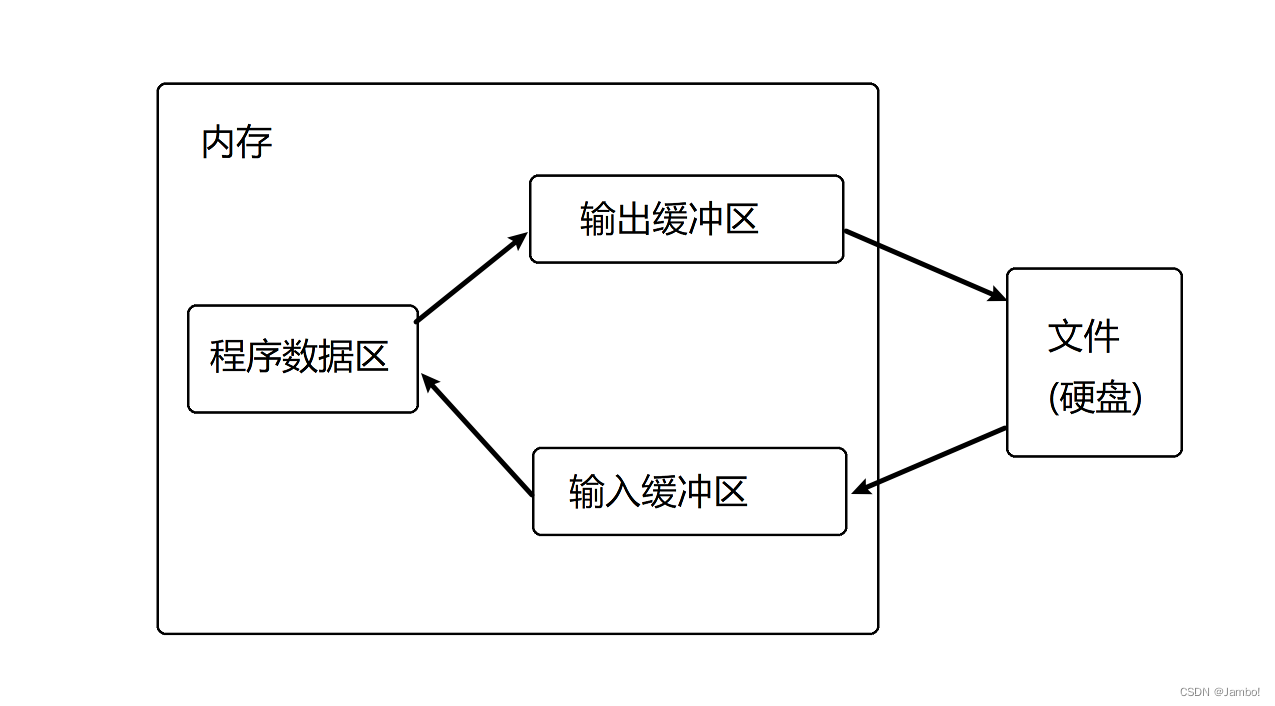
C语言文件操作
目录1.文件指针2.文件的打开和关闭3.文件的读写3.1文件的顺序读写fgetc和fputcfgets和fputsfscanf和fprintffread和fwrite3.2文件的随机读写fseekftellrewind4.文本文件和二进制文件5.文件读取结束的判定6.文件缓冲区1.文件指针 在文件操作中,一个关键的概念是文件…...
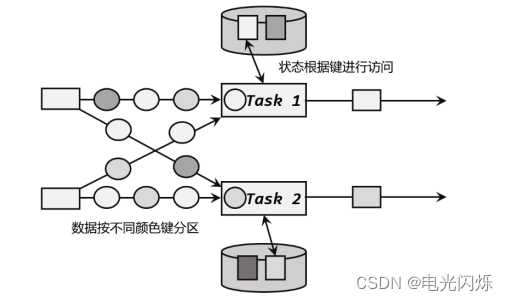
Flink中核心重点总结
目录 1. 算子链 1.1. 一对一(One-to-one, forwarding) 1.2. 重分区(Redistributing) 1.3. 为什么有算子链 2. 物理分区(Physical Partitioning) 2.1. 什么是分区 2.2. 随机分区ÿ…...

gismo中NURBS的相关函数的使用---待完善
文章目录 前言一、B样条的求值1.1 节点向量的生成1.2 基函数的调用1.3 函数里面的T指的是系数类型二、以等几何两个单元12个控制点为例输出的控制点坐标有误1.4二、#pic_center <table><tr><td bgcolor=PowderBlue>二维数2.12.22.32.4三、3.13.23.33.4四、4.…...

5.数据共享与持久化
数据共享与持久化 在容器中管理数据主要有两种方式: 数据卷(Data Volumes)挂载主机目录 (Bind mounts) 数据卷 数据卷是一个可供一个或多个容器使用的特殊目录,它绕过UFS,可以提供很多有用的特性: 数据…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
