高频算法:Leetcode53 最大子数组和
今天讲的是Leetcode第53题,最大子数组和
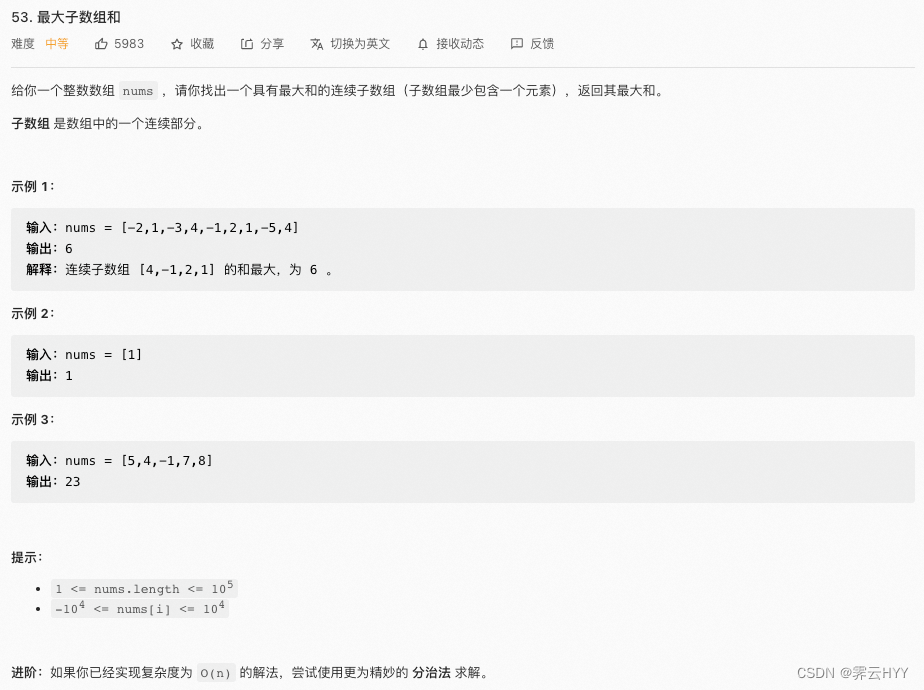
首先观察题目,题目需要我们找出具有最大和的连续子数组,直接拿题目中的示例来做一个演示,找一找什么规律下的连续子数组才能得到最大的和
先从-2开始,-2 + 1 = -1 此时我们的和是一个负数,那么无论后面的数是什么,这个数加上-1一定是更小了,所以-2这个值我们不应该加入到我们的结果子数组中
接下来是1 - 3 = -2,还是一个负数,跟上面一样,我们不需要负数,接下来的-3我们也不要了
此时从4开始找连续的子数组,4 - 1 = 3,是个正数,还能接受,就接着往后加
3 + 2 + 1 = 6,到这里为止,我们得到了迄今为止最大的子数组和
6 - 5 = 1,还是一个正数,还可以接着往后加,1 + 4 = 5,到这里为止整个数组都遍历完了
我们发现最大的子数组和是6,连续子数组为[4, -1, 2, 1]
通过我们对于示例的拆解,我们可以发现一个规律,那就是如果我们在遍历数组的时候,一旦加和为负数的话,这个和就对我们最终的解存在负面效果,所以当前遍历的数组元素就不会在我们的最大连续子数组中
同时我们在得到更大的和时,需要记录下来这个最大的值,因为后面的加和过程中,虽然整体是正数,但也不一定就是最大的,通过这两个条件我们就可以得到我们想要的最大和了
此时我们就可以得到本道题的第一个解法
public int maxSubArray(int[] nums) {int result = Integer.MIN_VALUE, sum = 0;for (int i = 0; i < nums.length; i++) {// 遍历数组并进行元素的累加sum += nums[i];// 如果返回的解小于当前我们当前子数组累加的和的话,就重新对解赋值,保证这个解一直是最大的if (result < sum) {result = sum;}// 如果子数组的和是负数的话,就舍弃掉当前已经遍历过的子数组,清零后接着往后遍历if (sum < 0) {sum = 0;}}return result;
}
通过上面发现的规律,我们还可以使用动态规划来解决这道题,首先需要明确的是状态转移方程是怎样的,先将当前的问题进行一下拆解,如果我们要得到最大子数组和,我们需要知道哪些子问题(依旧使用示例来描述)
- 如果我们的最大子数组包含-2,最大子数组是什么样的
- 如果我们的最大子数组包含1,最大子数组是什么样的
- 如果我们的最大子数组包含-3,最大子数组是什么样的
依次类推,直到数组中的最后一个元素… - 如果我们的最大子数组包含4,最大子数组是什么样的
但是这样定义的话,又不能明确当前这个元素是在数组的哪个位置,不满足动态规划的「无后效性」,简单来说就是有不确定性,这个时候,就需要将子问题定义的更加严格,直接指定子问题中的元素是子数组的最后一个元素,那么我们的子问题就变成了:
- 如果我们的最大子数组的最后一个元素是-2,最大子数组是什么样的
- 如果我们的最大子数组的最后一个元素是1,最大子数组是什么样的
- 如果我们的最大子数组的最后一个元素是-3,最大子数组是什么样的
… - 如果我们的最大子数组的最后一个元素是4,最大子数组是什么样的
子问题定义完了,那么我们的状态转移方程应该是什么样的呢?我们从第一个子问题出发梳理一下:
如果最后一个元素是-2,那么这个最大子数组其实就是[-2],因为也只有一个元素
如果最后一个元素是1,最大子数组和是 -2 + 1 = -1,这个情况下我们的状态转移方程是dp[i] = dp[i - 1] + nums[i];如果我们将1这个元素换成一个负数,比如说 -1,那么这个子数组和是 -2 - 1 = -3,所以最大子数组和就是 -1,-2就被舍弃掉了
最终我们得到的状态转移方程是dp[i] = Math.max(dp[i - 1] + nums[i], nums[i ])
通过上面的分析,我们可以写出使用动态规划来解决问题的代码
public int maxSubArray(int[] nums) {// 将第一个元素先赋值,这样即使数组只有一个元素也不会出问题int result = nums[0];int[] dp = new int[nums.length];// dp[0]的解是确定的dp[0] = nums[0];for (int i = 1; i < nums.length; i++) {// 状态转移方程dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);// 将子问题中最大的和存起来作为结果返回result = Math.max(result, dp[i]);}return result;
}
本人能力有限,可能理解表达不太到位,建议还是看Leetcode上大佬的题解来理解动态规划的思路官网题解
最后一种是题目中提到的分治法,分治法的核心思路也是将一个父问题拆成多个子问题来解决,还是拿题目的示例画一张图来理解一下
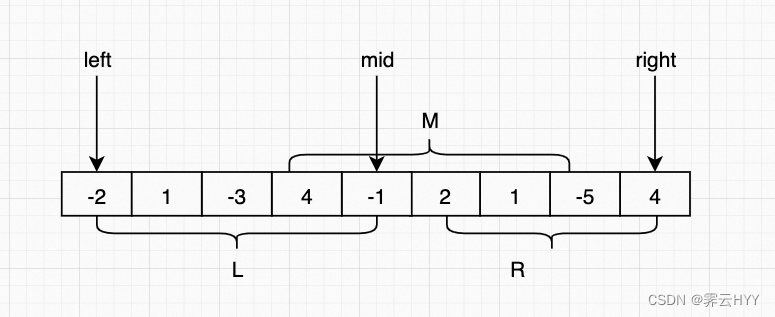
[-2,1,-3,4,-1,2,1,-5,4]作为一个完整的数组被分为3部分分别计算最大子数组和:
- L部分计算[left, mid]
- R部分计算[mid + 1, right]
- M部分计算包含mid和mid + 1这两个元素的部分,左边最长延伸到left,右边最长延伸到right
同时对于L和R这两个部分,又可以递归的往下计算分别的最大子数组和,比如L部分,[-2,1,-3,4,-1]这个数组可以继续往下进行分治,直到计算出结果为止
public int maxSubArray(int[] nums) {return maxSubArrayDivide(nums, 0, nums.length - 1);
}private int maxSubArrayDivide(int[] nums, int left, int right) {if (left == right) {return nums[left];}int mid = (right - left) / 2 + left;// 三个部分取最大的子数组和进行返回return Math.max(maxMid(nums, left, mid, right), Math.max(maxSubArrayDivide(nums, left, mid), maxSubArrayDivide(nums, mid + 1, right)));
}private int maxMid(int[] nums, int left, int mid, int right) {int sum = 0, leftSum = Integer.MIN_VALUE, rightSum = Integer.MIN_VALUE;// 遍历[left, mid]这个范围内最大的子数组和for (int i = mid; i >= left; i--) {sum += nums[i];if (leftSum < sum) {leftSum = sum;}}sum = 0;// 遍历[mid + 1, right]这个范围内最大的子数组和for (int i = mid + 1; i <= right; i++) {sum += nums[i];if (rightSum < sum) {rightSum = sum;}}return leftSum + rightSum;
}
相关文章:

高频算法:Leetcode53 最大子数组和
今天讲的是Leetcode第53题,最大子数组和 首先观察题目,题目需要我们找出具有最大和的连续子数组,直接拿题目中的示例来做一个演示,找一找什么规律下的连续子数组才能得到最大的和 先从-2开始,-2 1 -1 此时我们的和…...
如何编写接口自动化测试框架、
编写接口自动化测试框架需要注意以下几点: 接口选择:首先确定需要测试的接口,包括请求方式、URL、参数、返回值等信息。 框架设计:设计一个灵活的框架,可以根据接口类型(RESTful API、SOAP API等ÿ…...

【Java面试八股文宝典之RabbitMQ篇】备战2023 查缺补漏 你越早准备 越早成功!!!——Day17
大家好,我是陶然同学,软件工程大三即将实习。认识我的朋友们知道,我是科班出身,学的还行,但是对面试掌握不够,所以我将用这100多天更新Java面试题🙃🙃。 不敢苟同,相信大…...
ESP32开发(1)----Espressif-IDE开发环境配置
Espressif-IDE开发环境配置前言一、ESP32-WROOM-32介绍二、IDE环境搭建三、建立第一个项目总结前言 最近得到一块ESP32-WROOM-32的开发板,没有原理图,但板子走线比较简单,看着板子上的布线大致猜一猜连接,然后试玩了一下…...
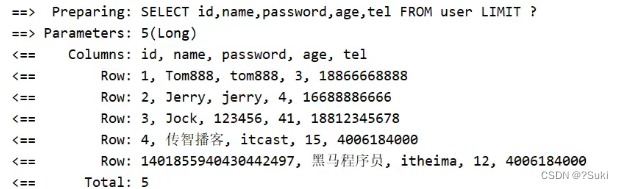
MyBatisPlus标准数据层开发
MyBatisPlus标准数据层开发2,标准数据层开发2.1 标准CRUD使用2.2 新增2.3 删除2.4 修改2.5 根据ID查询2.6 查询所有2.7 Lombok概念使用步骤步骤1:添加lombok依赖步骤2:安装Lombok的插件步骤3:模型类上添加注解2.8 分页功能步骤1:调用方法传入参数获取返回值步骤2:设…...

C/C++每日一练(20230412)
目录 1. 二维数组找最值 🌟🌟 2. 排序 🌟 3. 二叉树展开为链表 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 二维…...
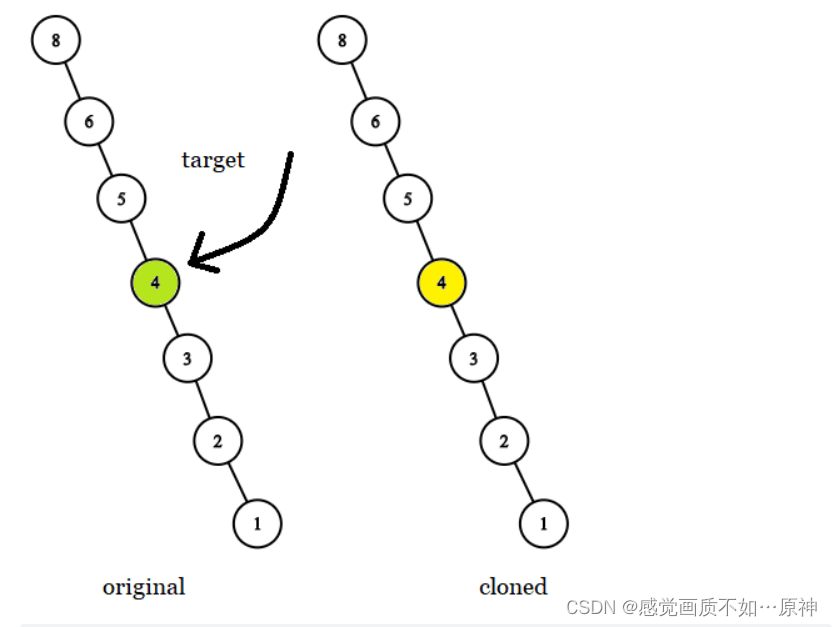
Leetcode.1379 找出克隆二叉树中的相同节点
题目链接 Leetcode.1379 找出克隆二叉树中的相同节点 easy 题目描述 给你两棵二叉树,原始树 original和克隆树 cloned,以及一个位于原始树 original中的目标节点 target。 其中,克隆树 cloned是原始树 original的一个 副本 。 请找出在树 …...

2022年团体程序设计天梯赛-总决赛
目录 一、L1-1 今天我要赢 二、L1-2 种钻石 三、L1-3 谁能进图书馆 四、L1-4 拯救外星人 五、L1-5 试试手气 六、L1-6 斯德哥尔摩火车上的题 七、L1-7 机工士姆斯塔迪奥 八、L1-8 静静的推荐 九、L2-1 插松枝 十、L2-2 老板的作息表 十一、L2-3 龙龙送外卖 十二、L…...
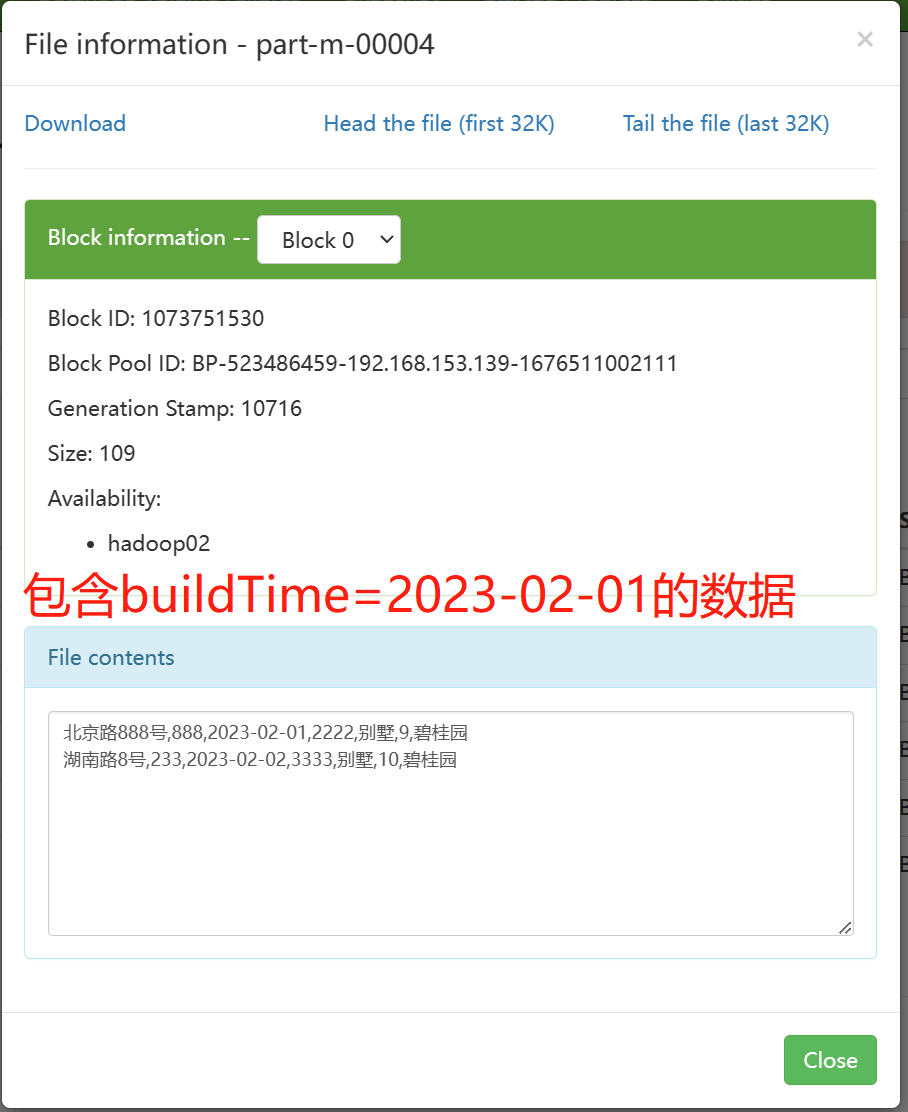
大数据技术之Sqoop——SQL to Hadoop
一、简介sqoop (sql to hadoop)是一款开源的工具,主要用于在 Hadoop(Hive)与传统的数据库(mysql、postgresql...)间进行数据的传递,可以将一个关系型数据库(例如 : MSQL,Oracle,Post…...

Java议题
序号议题 解释MyBatis官网1mapper文件中什么时候使用 # 什么时候必须用 $ 1、关键字作为参数,使用"$",两边不加""。 2、非关键字作为参数,使用"#"防注入。 其他情况优先使用"#" 2主键回填࿰…...
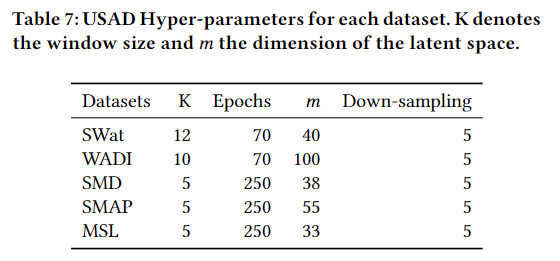
【阅读论文】USAD:多变量时间序列上的无监督异常检测
USAD : UnSupervised Anomaly Detection on Multivariate Time Series 摘要 IT系统的自动监控是Orange目前面临的挑战。考虑到其IT运营所达到的规模和复杂性,随着时间的推移,用于推断正常和异常行为的测量所需的传感器数量急剧增加,使得传统…...

Java多线程:ReentrantLock中的方法
公平锁与非公平锁 ReentrantLock有一个很大的特点,就是可以指定锁是公平锁还是非公平锁,公平锁表示线程获取锁的顺序是按照线程排队的顺序来分配的,而非公平锁就是一种获取锁的抢占机制,是随机获得锁的,先来的未必就一…...

RabbitMQ初识快速入门
RabbitMQ初识&快速入门1.初识MQ1.1.同步和异步通讯1.1.1.同步通讯1.1.2.异步通讯1.2.技术对比:2.快速入门2.1.安装RabbitMQ2.1.1 下载镜像2.1.2 安装MQ2.2.RabbitMQ消息模型2.3.导入Demo工程2.4.入门案例2.4.1.publisher实现2.4.2.consumer实现2.5.总结1.初识MQ…...
由浅入深了解HashMap源码
由经典面试题引入,讲解一下HashMap的底层数据结构?这个面试题你当然可以只答,HashMap底层的数据结构是由(数组链表红黑树)实现的,但是显然面试官不太满意这个答案,毕竟这里有一个坑需要你去填&a…...
P5318 【深基18.例3】查找文献
题目描述 小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个(也有可能没有)参考文献的链接指向别的博客文章。小K 求知欲旺盛,如果他看了某篇文章,那么他一定会去看这篇文章的参考文献(如果他之前已经看过这篇参考…...

Error caught was: No module named ‘triton‘
虽然报错但是不影响程序运行: A matching Triton is not available, some optimizations will not be enabled. Error caught was: No module named triton解决: pip install -i https://pypi.tuna.tsinghua.edu.cn/simple triton2.0.0.dev20221120...

Ruby设计-开发日志
Log 1 产品 Product 1.1 创建 Product 创建名为 project 的 rails 应用 rails new project创建 Product 模型 rails generate scaffold Product title:string description:text image_url:string price:decimal这会生成一个 migration ,我们需要进一步修改这个…...

SpringBoot 调用外部接口的三种方式
方式一:使用原始httpClient请求 /** description get方式获取入参,插入数据并发起流程* params documentId* return String*/ RequestMapping("/submit/{documentId}") public String submit1(PathVariable String documentId) throws ParseE…...
C 中的结构体
C 中的结构体 C 数组允许定义可存储相同类型数据项的变量,结构是 C 编程中另一种用户自定义的可用的数据类型,它允许您存储不同类型的数据项。 结构体中的数据成员可以是基本数据类型(如 int、float、char 等),也可以…...

nodejs安装教程
Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行时,可以用于在服务器端运行 JavaScript 代码。以下是 Node.js 的安装教程: 步骤 1:下载 Node.js 访问 Node.js 的官方网站 https://nodejs.org/,进入官方下载页面。 在下载页…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
