算法学习day51
算法学习day51
- 1.力扣309.最佳买卖股票时机含冷冻期
- 1.1 题目描述
- 1.2分析
- 1.3 代码
- 2.力扣714.买卖股票的最佳时机含手续费
- 2.1 题目描述
- 2.2 分析
- 2.3 代码
- 3.参考资料
1.力扣309.最佳买卖股票时机含冷冻期
1.1 题目描述
题目描述
给定一个整数数组,其中第i个元素代表了第i天的股票价格。
设计一个算法求最大利润。在满足以下约束条件下,尽可能多的完成交易:
(1)你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
(2)卖出股票后,你无法在第二天买入股票(冷冻期为1天)
例:
输入:[1,2,3,0,2]
输出:3
解释:对应的交易状态为:[买入,卖出,冷冻期,买入,卖出]
1.2分析
动规五部曲
1.确定dp数组以及下标的含义
dp[i] [j]:第i天状态为j,所剩的最多现金为dp[i] [j]
dp[i] [0]: 持有股票(今天买入股票,或者之前买入后没有操作了,一直持有)
dp[i] [1]:保持卖出股票的状态(度过了冷冻起之后,一直没有操作)
dp[i] [2]:今天卖出股票
dp[i] [3]: 今天为冷冻期,但冷冻期状态不可持续
2.确定递推公式
dp[i] [0]: 持有股票(今天买入股票,或者之前买入后没有操作了,一直持有)
(1)前一天持有股票的状态,dp[i] [0] = dp[i - 1] [0]
(2)今天买入:
(2.1)前一天是冷冻期,然后今天买入,dp[i - 1] [3] - prices[i]
(2.2)前一天保持卖出股票状态,dp[ i -1] [1] - prices[i]
递推公式: dp[i] [0] = max(dp[i - 1] [0] , dp[i - 1] [3] - prices[i] , dp[ i -1] [1] - prices[i])
**dp[i] [1]:**保持卖出股票的状态(度过了冷冻起之后,一直没有操作)
(1) 前一天就卖出股票了
(2) 前一天是冷冻期
递推公式: dp[i] [1] = max(dp[i - 1] [1], dp[i - 1] [3])
**dp[i] [2]:**今天卖出股票
今天卖出,说明昨天一定持有
递推公式:dp[i] [2] = dp[i - 1] [0] + prices[i]
dp[i] [3]: 今天为冷冻期,但冷冻期状态不可持续
到达冷淡期,说明昨天卖出了股票
递推公式:dp[i] [3] = dp[i - 1] [2]
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
3.dp数组如何初始化
dp[0] [0] = -prices[0]
dp[0] [1] = 0
dp[0] [2] = 0
dp[0] [3] = 0
4.确定遍历顺序
显然从前往后遍历
5.举例推导dp数组

1.3 代码
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();if (n == 0) return 0;vector<vector<int>> dp(n, vector<int>(4, 0)); // 创建一个 n 行 4 列的二维数组 dp,用于记录各个状态下的最大收益dp[0][0] -= prices[0]; // 初始状态为持有股票状态,因此要减去第一天股票价格for (int i = 1; i < n; i++) { // 从第二天开始遍历// 当前状态为持有股票状态,可以是前一天就持有股票状态,也可以是今天买入了股票,要选择收益最大的一种情况dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i])); // 当前状态为保持卖出股票状态,可以是两天前就卖出了股票,也可以是前一天就是卖出股票状态,要选择收益最大的一种情况dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]); // 当前状态为今天卖出股票状态,由于前一天必须持有股票状态,因此从持有股票状态转移过来dp[i][2] = dp[i - 1][0] + prices[i]; // 当前状态为今天为冷冻期状态,前一天必须是卖出股票状态,因此从卖出股票状态转移过来dp[i][3] = dp[i - 1][2];}// 最终收益可能来自于保持卖出股票状态、今天卖出股票状态或今天为冷冻期状态,取最大值return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2])); }
};2.力扣714.买卖股票的最佳时机含手续费
2.1 题目描述
题目描述:
给定一个整数数组prices , 其中第i个元素代表了第i天的股票价格;非负整数fee代表了交易的手续费。
可以无限次交易,但是每一笔交易都需要手续费。如果你已经购买了一个股票,在卖出它之前不能在继续购买股票了。
返回获得利润的最大值。
例:
输入:prices = [1, 3, 2, 8, 4, 9] , fee= 2
输出: 8
- 在此处买入 prices[0] = 1
- 在此处卖出 prices[3] = 8
- 在此处买入 prices[4] = 4
- 在此处卖出 prices[5] = 9
- 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
2.2 分析
dp[i] [0] 表示第i天持有股票所省最多现金。dp[i] [1] 表示第i天不持有股票所得最多现金
1.dp[i] [0] 表示第i天持有股票所省最多现金由以下状态推导出来:
(1) 第i -1 就持有股票,保持现状,所得现金就是昨天持有股票所得现金,dp[i- 1] [0]
(2) 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去今天的股票价格,dp[i - 1] [1] - prices[i]
递推公式:dp[i] [0] = max(dp[i-1] [0], dp[i - 1] [1] - prices[i])
2.dp[i] [1] 表示第i天不持有股票所得最多现金
(1)如果第i -1 就不持有股票,保持现状,所得现金就是昨天不持有股票的现金,dp[i-1] [1]
(2) 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金,需要手续费,dp[i - 1] [0] + prices[i] - fee
递推公式:dp[ i ] [1] = max(dp[i - 1] [1] , dp[ i- 1] [0] + prices[i] - fee)
2.3 代码
class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();// 定义 dp 数组,dp[i][0/1] 表示第 i 天结束时,// 持有股票/不持有股票的最大收益vector<vector<int>> dp(n, vector<int>(2, 0));dp[0][0] -= prices[0]; // 第一天持股,花费 prices[0] 的成本for (int i = 1; i < n; i++) {// 第 i 天结束时持有股票的最大收益分两种情况:// 1. 前一天也持有股票,今天不进行任何操作,所以今天的最大收益就是昨天的最大收益// 2. 前一天不持有股票,今天买入股票,所以今天的最大收益就是前一天不持有股票时的最大收益减去今天的股票价格dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);// 第 i 天结束时不持有股票的最大收益也分两种情况:// 1. 前一天也不持有股票,今天不进行任何操作,所以今天的最大收益就是昨天的最大收益// 2. 前一天持有股票,今天卖出股票,所以今天的最大收益就是前一天持有股票时的最大收益加上今天的股票价格减去手续费dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);}// 返回最后一天结束时,持有股票和不持有股票两种状态中的最大收益return max(dp[n - 1][0], dp[n - 1][1]);}
};3.参考资料
[代码随想录]
相关文章:

算法学习day51
算法学习day511.力扣309.最佳买卖股票时机含冷冻期1.1 题目描述1.2分析1.3 代码2.力扣714.买卖股票的最佳时机含手续费2.1 题目描述2.2 分析2.3 代码3.参考资料1.力扣309.最佳买卖股票时机含冷冻期 1.1 题目描述 题目描述 给定一个整数数组,其中第i个元素代表了第…...

10 JS01——初识JS
目标: 1、初识JavaScript 2、JavaScript注释 3、JavaScript输入输出语句 一、初识JavaScript 1、JavaScript是什么 JavaScript是世界上最流行的语言之一,是一种运行在客户端的脚本语言(Script是脚本的意思) 脚本语言:不需要编译,运行过程…...

【软考备考-综合知识】安全性、可靠性与系统性能评测基础知识
计算机的安全性 安全等级 计算机系统中的三类安全性是指技术安全性、管理安全性和政策法律安全性。 信息安全五要素 机密性:全包信息不暴露给未授权的实体或进程。 完整性:只有得到允许的人才能够修改数据,并能够判别出数据是否已被篡改。…...

匆忙之间难免疏忽,写代码更加如此
一个方法包含了多个知识点的合计,合计起来用。实战开发特点1; 基础知识点不牢固,您必定就会感觉寸步难行啊 public class AddJiChuShu{int a 1;int b 2;int c 0;int d 0;string str "";string str2 "张三";//mothe…...
低代码平台后端技术选型2.0)
低代码(七)低代码平台后端技术选型2.0
JWT 登录token Json web token (JWT), 是为了在网络应用环境间传递声明而执行的一种基于JSON的开放标准((RFC 7519).该token被设计为紧凑且安全的,特别适用于分布式站点的单点登录(SSO)场景。JWT的声明一般被用来在身份提供者和服…...

UDS介绍
首先要有网络网络七层的概念: 学习链接: 七层网络模型-CSDN博客 UDS网络层/TP层(ISO 15765-2)的解读 - 知乎 (zhihu.com) 概念: UDS(Unified Diagnostic Services,统一的诊断服务。 标准名是《…...
ASP.NET Core MVC 从入门到精通之初窥门径
随着技术的发展,ASP.NET Core MVC也推出了好长时间,经过不断的版本更新迭代,已经越来越完善,本系列文章主要讲解ASP.NET Core MVC开发B/S系统过程中所涉及到的相关内容,适用于初学者,在校毕业生,…...

英码科技智慧环卫:构建宜居城市新篇章
随着城市化进程的加快,城市环境卫生问题日益凸显。如何提高城市环境卫生管理水平,提升城市品质,成为了各级政府和社会各界关注的焦点。智慧环卫作为一种结合现代信息技术的环境卫生管理方式,正在逐渐成为解决城市环境卫生问题的有…...

在Spring Boot微服务使用HashOperations操作Redis Hash哈希散列
记录:403 场景:在Spring Boot微服务使用RedisTemplate的HashOperations操作Redis Hash哈希散列。 版本:JDK 1.8,Spring Boot 2.6.3,redis-6.2.5 1.微服务中Redis配置信息 1.1在application.yml中Redis配置信息 spring:redis:host: 192.1…...

innobackupex备份mysql产生returned OS error 124
解决使用innobackupex备份mysql产生returned OS error 124 xtrabackup 报错Too many open files 故障处理 一、背景 客户反馈数据库备份失败。 二、环境描述 [rootmes-node1 ~]# mysql -V mysql Ver 14.14 Distrib 5.7.24, for Linux (x86_64) using EditLine wrapper [root…...
明明有index.jsp文件访问的时候却显示404
重建一下项目...

人工智能前沿——「全域全知全能」人类新宇宙ChatGPT
🚀🚀🚀OpenAI聊天机器人ChatGPT——「全域全知全能」人类全宇宙大爆炸!!🔥🔥🔥 一、什么是ChatGPT?🍀🍀 ChatGPT是生成型预训练变换模型(Chat G…...

eslint-plugin-import - import/order
eslint-plugin-import是什么? 该插件目的在于支持ES6以上的导入/导出语法,并防止文件路径和导入名称拼写错误的问题。 import/order是什么? 按照约定的规则对引入的模块进行排序。 import/order常用规则介绍 groups 约定引入模块顺序的…...

selenium知识点大全
selenium知识点大全 在使用selenium之前必须先配置浏览器对应版本的webdriver。 1. 初始化浏览器对象 from selenium.webdriver import Chrome# 创建浏览器对象,并且打开一个空的页面 browser Chrome()# 关闭浏览器 browser.close()2. 访问指定网页 from selen…...
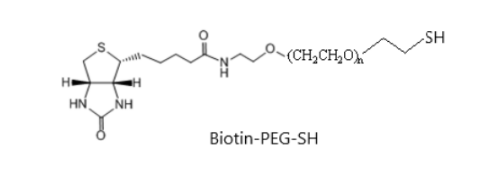
Biotin-PEG-SH生物素-聚乙二醇-巯基结构式;SH-PEG-Biotin
Biotin-PEG-SH 生物素-聚乙二醇-巯基 中文名称:生物素-聚乙二醇-巯基 英文名称:Biotin-PEG-SH Biotin-PEG-Thiol 性状:粘稠液体或者固体粉末,取决于分子量 溶剂:溶于水和DCM、DMF等大部分有机溶剂 分子式&#x…...
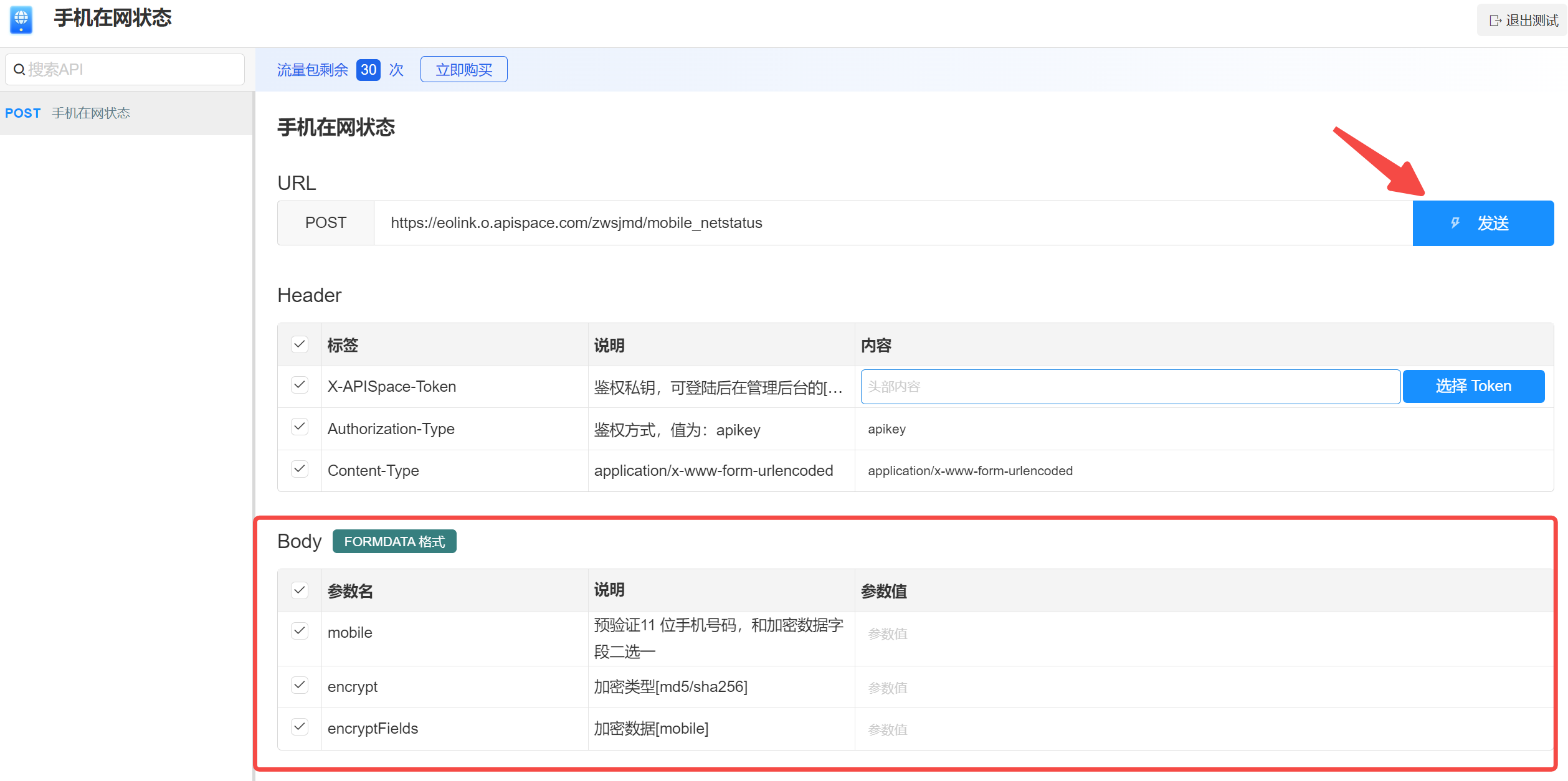
【防止恶意用户注册】-- 手机在网状态 API 的防欺诈应用解析
简介 手机在网状态 API 支持传入手机号码,查询手机号在网状态,返回在网、在网不可用、不在网(销号/未启用/停机)等多种状态,查询手机号在网状态之后,可以根据具体的业务需求来进行不同的处理。 本文主要介…...

Python json 数据提取 jsonpath 详解
一、JsonPath JsonPath 是一种信息抽取类库,是从JSON文档中抽取指定信息的工具,提供多种语言实现版本,包括:Javascript, Python, PHP 和 Java。也就是独立的可以配合多种语言进行匹配的目标值的一种类库,和…...
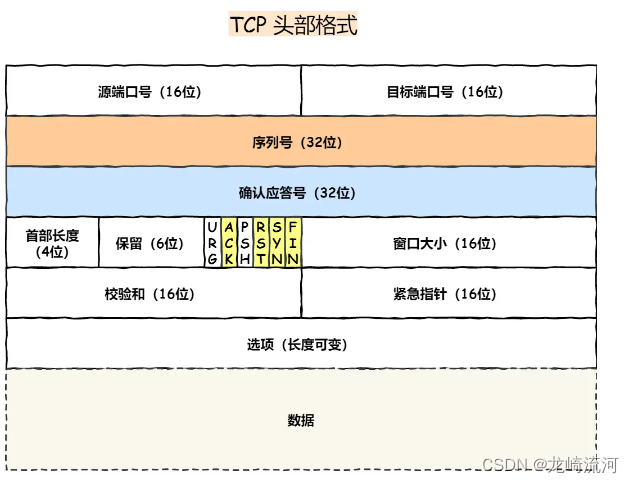
TCP和UDP的区别以及应用场景
区别 首先UDP协议非常简单,头部只有8个字节: 校验和为了提供可靠的UDP首部和数据而设计,防止收到在网络传输中受损的UDP包。 再对比下TCP协议: 传输层有两个传输协议分别是 TCP 和 UDP,在内核中是两个完全独立的软件…...

高铁轮毂表面缺陷的<视觉显著性>超像素图像检测方法
内容:提出一种基于视觉显著性注意机制的超像素自适应检测方法; 设计视觉显著性注意机制滤波器用于粗略定位出缺陷空间范围,结合超像素分块图像分割方法消除光照不均匀引起的噪声干扰,有效地完成缺陷区域的边界分割和实时特征提取&…...

纺织工业库房如何有效防潮?恒温恒湿真的有效吗?
纺织工业库房中的设备或存放的货物对温度或湿度的变化又非常敏感,温度或湿度的波动可能会产生一些问题。 针对库房环境温湿度的监测,若采用人工检测的方式,很难管控精准且工作效率低;其次,人工综合成本高。那么该如何实…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
