初级算法-栈与队列
主要记录算法和数据结构学习笔记,新的一年更上一层楼!
初级算法-栈与队列
- 一、栈实现队列
- 二、队列实现栈
- 三、有效的括号
- 四、删除字符串中的所有相邻重复项
- 五、逆波兰表达式求值
- 六、滑动窗口最大值
- 七、前K个高频元素
- 栈先进后出,不提供走访功能和迭代器
- 递归、表达式求值、括号匹配、进制转换一般利用栈
- 队列先进先出
- 满队列:front==(rear+1)%m
- 循环队列出队操作 front = (front+1) % (m+1)
- 循环队列,f 队头,r 队尾,队列中的元素个数为 (r-f+MAX+1) % MAX
- 循环队列队空:rear==front;队满:front == (rear+1) % MAX
- 链接方式存储队列,进行插入运算时 常修改尾指针,插入前为空,头尾都需修改。
- 循环队列:尾指针-头指针+容量,front小于rear时N-front+rear
一、栈实现队列
1.题目:使用栈实现队列的下列操作:
push(x) – 将一个元素放入队列的尾部。
pop() – 从队列首部移除元素。
peek() – 返回队列首部的元素。
empty() – 返回队列是否为空。
示例
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // 返回 1
queue.pop(); // 返回 1
queue.empty(); // 返回 false
说明:
你只能使用标准的栈操作 – 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)。
2.解题思路:
// 使用两个数组的栈方法(push, pop) 实现队列
/**
* Initialize your data structure here.
*/
var MyQueue = function() {this.stackIn = [];this.stackOut = [];
};/**
* Push element x to the back of queue.
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {this.stackIn.push(x);
};/**
* Removes the element from in front of queue and returns that element.
* @return {number}
*/
MyQueue.prototype.pop = function() {const size = this.stackOut.length;if(size) {return this.stackOut.pop();}while(this.stackIn.length) {this.stackOut.push(this.stackIn.pop());}return this.stackOut.pop();
};/**
* Get the front element.
* @return {number}
*/
MyQueue.prototype.peek = function() {const x = this.pop();this.stackOut.push(x);return x;
};/**
* Returns whether the queue is empty.
* @return {boolean}
*/
MyQueue.prototype.empty = function() {return !this.stackIn.length && !this.stackOut.length
};
// 运行时间:60ms
// 内存消耗:40.8MB
二、队列实现栈
1.题目:使用队列实现栈的下列操作:
push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空
注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
2.解题思路:
// 使用两个队列实现
/*** Initialize your data structure here.*/
var MyStack = function() {this.queue1 = [];this.queue2 = [];
};/*** Push element x onto stack. * @param {number} x* @return {void}*/
MyStack.prototype.push = function(x) {this.queue1.push(x);
};/*** Removes the element on top of the stack and returns that element.* @return {number}*/
MyStack.prototype.pop = function() {// 减少两个队列交换的次数, 只有当queue1为空时,交换两个队列if(!this.queue1.length) {[this.queue1, this.queue2] = [this.queue2, this.queue1];}while(this.queue1.length > 1) {this.queue2.push(this.queue1.shift());}return this.queue1.shift();
};/*** Get the top element.* @return {number}*/
MyStack.prototype.top = function() {const x = this.pop();this.queue1.push(x);return x;
};/*** Returns whether the stack is empty.* @return {boolean}*/
MyStack.prototype.empty = function() {return !this.queue1.length && !this.queue2.length;
};// 运行时间:64ms
// 内存消耗:40.9MB
// 使用一个队列实现
/*** Initialize your data structure here.*/
var MyStack = function() {this.queue = [];
};/*** Push element x onto stack. * @param {number} x* @return {void}*/
MyStack.prototype.push = function(x) {this.queue.push(x);
};/*** Removes the element on top of the stack and returns that element.* @return {number}*/
MyStack.prototype.pop = function() {let size = this.queue.length;while(size-- > 1) {this.queue.push(this.queue.shift());}return this.queue.shift();
};/*** Get the top element.* @return {number}*/
MyStack.prototype.top = function() {const x = this.pop();this.queue.push(x);return x;
};/*** Returns whether the stack is empty.* @return {boolean}*/
MyStack.prototype.empty = function() {return !this.queue.length;
};// 运行时间:76ms
// 内存消耗:41.1MB
三、有效的括号
1.题目:
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例
示例 1:输入: "()"
输出: true
示例 2:输入: "()[]{}"
输出: true
示例 3:输入: "(]"
输出: false
示例 4:输入: "([)]"
输出: false
示例 5:输入: "{[]}"
输出: true
2.解题思路:
var isValid = function (s) {const stack = [];for (let i = 0; i < s.length; i++) {let c = s[i];switch (c) {case '(':stack.push(')');break;case '[':stack.push(']');break;case '{':stack.push('}');break;default:if (c !== stack.pop()) {return false;}}}return stack.length === 0;
};
// 简化版本
var isValid = function(s) {const stack = [], map = {"(":")","{":"}","[":"]"};for(const x of s) {if(x in map) {stack.push(x);continue;};if(map[stack.pop()] !== x) return false;}return !stack.length;
};
// 运行时间:52ms
// 内存消耗:41.6MB
四、删除字符串中的所有相邻重复项
1.题目:
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例
输入:"abbaca"
输出:"ca"
解释:例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
提示:
1 <= S.length <= 20000
S 仅由小写英文字母组成。
2.解题思路:
// 使用栈
var removeDuplicates = function(s) {const stack = [];for(const x of s) {let c = null;if(stack.length && x === (c = stack.pop())) continue;c && stack.push(c);stack.push(x);}return stack.join("");
};
// 运行时间:76ms
// 内存消耗:51.1MB
// 原地解法(双指针模拟栈)
var removeDuplicates = function(s) {s = [...s];let top = -1; // 指向栈顶元素的下标for(let i = 0; i < s.length; i++) {if(top === -1 || s[top] !== s[i]) { // top === -1 即空栈s[++top] = s[i]; // 入栈} else {top--; // 推出栈}}s.length = top + 1; // 栈顶元素下标 + 1 为栈的长度return s.join('');
};
// 运行时间:64ms
// 内存消耗:46.8MB
五、逆波兰表达式求值
1.题目
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 + , - , * , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例
示例 1:输入: ["2", "1", "+", "3", " * "]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:输入: ["4", "13", "5", "/", "+"]
输出: 6
解释: 该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:输入: ["10", "6", "9", "3", "+", "-11", " * ", "/", " * ", "17", "+", "5", "+"]输出: 22解释:该算式转化为常见的中缀算术表达式为:((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
逆波兰表达式:是一种后缀表达式,所谓后缀就是指运算符写在后面。平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。逆波兰表达式主要有以下两个优点:-去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。-适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中。
2.解题思路:
var evalRPN = function (tokens) {const stack = [];for (const token of tokens) {if (isNaN(Number(token))) { // 非数字const n2 = stack.pop(); // 出栈两个数字const n1 = stack.pop();switch (token) { // 判断运算符类型,算出新数入栈case "+":stack.push(n1 + n2);break;case "-":stack.push(n1 - n2);break;case "*":stack.push(n1 * n2);break;case "/":stack.push(n1 / n2 | 0);break;}} else { // 数字stack.push(Number(token));}}return stack[0]; // 因没有遇到运算符而待在栈中的结果
};
// 运行时间:64ms
// 内存消耗:43.8MB
六、滑动窗口最大值
1.题目:给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例
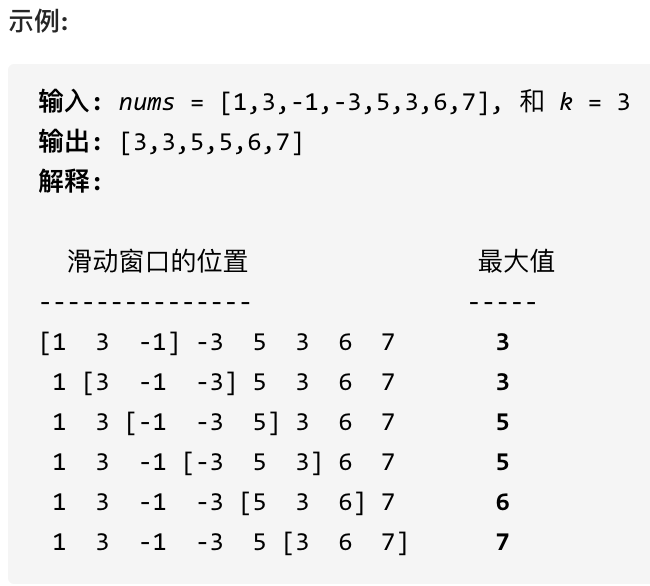
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length
2.解题思路:
/*** @param {number[]} nums* @param {number} k* @return {number[]}*/
var maxSlidingWindow = function (nums, k) {class MonoQueue {queue;constructor() {this.queue = [];}enqueue(value) {let back = this.queue[this.queue.length - 1];while (back !== undefined && back < value) {this.queue.pop();back = this.queue[this.queue.length - 1];}this.queue.push(value);}dequeue(value) {let front = this.front();if (front === value) {this.queue.shift();}}front() {return this.queue[0];}}let helperQueue = new MonoQueue();let i = 0, j = 0;let resArr = [];while (j < k) {helperQueue.enqueue(nums[j++]);}resArr.push(helperQueue.front());while (j < nums.length) {helperQueue.enqueue(nums[j]);helperQueue.dequeue(nums[i]);resArr.push(helperQueue.front());i++, j++;}return resArr;
};
#运行时间:8528ms
#内存消耗:75.3MB
七、前K个高频元素
1.题目:
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例
示例 1:输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:输入: nums = [1], k = 1
输出: [1]
提示:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(nlogn)O(n \log n)O(nlogn) , n 是数组的大小。
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
你可以按任意顺序返回答案。
// js 没有堆 需要自己构造
class Heap {constructor(compareFn) {this.compareFn = compareFn;this.queue = [];}// 添加push(item) {// 推入元素this.queue.push(item);// 上浮let index = this.size() - 1; // 记录推入元素下标let parent = Math.floor((index - 1) / 2); // 记录父节点下标while (parent >= 0 && this.compare(parent, index) > 0) { // 注意compare参数顺序[this.queue[index], this.queue[parent]] = [this.queue[parent], this.queue[index]];// 更新下标index = parent;parent = Math.floor((index - 1) / 2);}}// 获取堆顶元素并移除pop() {// 堆顶元素const out = this.queue[0];// 移除堆顶元素 填入最后一个元素this.queue[0] = this.queue.pop();// 下沉let index = 0; // 记录下沉元素下标let left = 1; // left 是左子节点下标 left + 1 则是右子节点下标let searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;while (searchChild !== undefined && this.compare(index, searchChild) > 0) { // 注意compare参数顺序[this.queue[index], this.queue[searchChild]] = [this.queue[searchChild], this.queue[index]];// 更新下标index = searchChild;left = 2 * index + 1;searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;}return out;}size() {return this.queue.length;}// 使用传入的 compareFn 比较两个位置的元素compare(index1, index2) {// 处理下标越界问题if (this.queue[index1] === undefined) return 1;if (this.queue[index2] === undefined) return -1;return this.compareFn(this.queue[index1], this.queue[index2]);}}const topKFrequent = function (nums, k) {const map = new Map();for (const num of nums) {map.set(num, (map.get(num) || 0) + 1);}// 创建小顶堆const heap= new Heap((a, b) => a[1] - b[1]);// entry 是一个长度为2的数组,0位置存储key,1位置存储valuefor (const entry of map.entries()) {heap.push(entry);if (heap.size() > k) {heap.pop();}}// return heap.queue.map(e => e[0]);const res = [];for (let i = heap.size() - 1; i >= 0; i--) {res[i] = heap.pop()[0];}return res;
};
#运行时间:88ms
#内存消耗:44.4MB
相关文章:

初级算法-栈与队列
主要记录算法和数据结构学习笔记,新的一年更上一层楼! 初级算法-栈与队列一、栈实现队列二、队列实现栈三、有效的括号四、删除字符串中的所有相邻重复项五、逆波兰表达式求值六、滑动窗口最大值七、前K个高频元素栈先进后出,不提供走访功能…...

菜鸟教程之Android学习笔记Service
Service初步 一、StartService启动Service的调用顺序 MainActivity.java package com.example.test2;import androidx.appcompat.app.AppCompatActivity;import android.app.Activity; import android.content.Intent; import android.os.Bundle; import android.view.View;…...

半个月狂飙1000亿,ChatGPT概念股凭什么?
ChatGPT 掀起了AI股历史上最疯狂的一轮市值狂飙。 自春节后至今,ChatGPT概念股开始了暴走模式,短短半月时间,海天瑞声、开普云等ChatGPT概念股市值累计增加了近1400亿。 如此的爆炸效应,得益于ChatGPT所展现出商业化落地的巨大潜…...

linux使用systemctl
要使用 systemd 来控制 frps,需要先安装 systemd,然后在 /etc/systemd/system 目录下创建一个 frps.service 文件 安装systemd # yum yum install systemd # apt apt install systemd创建并编辑 frps.service 文件 [Unit] DescriptionFrp Server Serv…...

交换机和VLAN简介
一.二层设备(交换机和网桥)的区别简介 1.交换机: 2.网桥: 二.交换机原理介绍 三.VLAN概念介绍 1.VLAN将一个物理区域LAN划分为多个区域 2.作用: 3.标识方式VLAN ID 4.VLAN配置下MAC地址表的三元素 5.交换中的…...

想要拯救丢失的海康威视硬盘录像数据?可采用这三种恢复方法
海康威视作为全球领先的视频监控产品及解决方案提供商,其硬盘录像机可用于对大型公共场所、企事业单位及个人住宅等场所的安全监控。然而在实际使用中,有时会发生硬盘录像数据丢失的情况,这将对用户带来不小的损失和困扰。 硬盘录像数据丢失…...
大整数乘整数)
每周一算法:高精度乘法(一)大整数乘整数
高精度乘法 乘法是我们在比赛中常用到运算之一,但在利用C++进行乘方或者阶乘计算时,由于其结果的增长速度很快,很容易就溢出了。例如: 13 ! = 6 , 227 , 020 , 800 13!=6,227,020,800 13!=6...

c++华为od面经
手撕代码: 力扣1004 最大连续1的个数 给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 输入:nums [1,1,1,0,0,0,1,1,1,1,0], K 2 输出:6 解释:[1,1,1…...
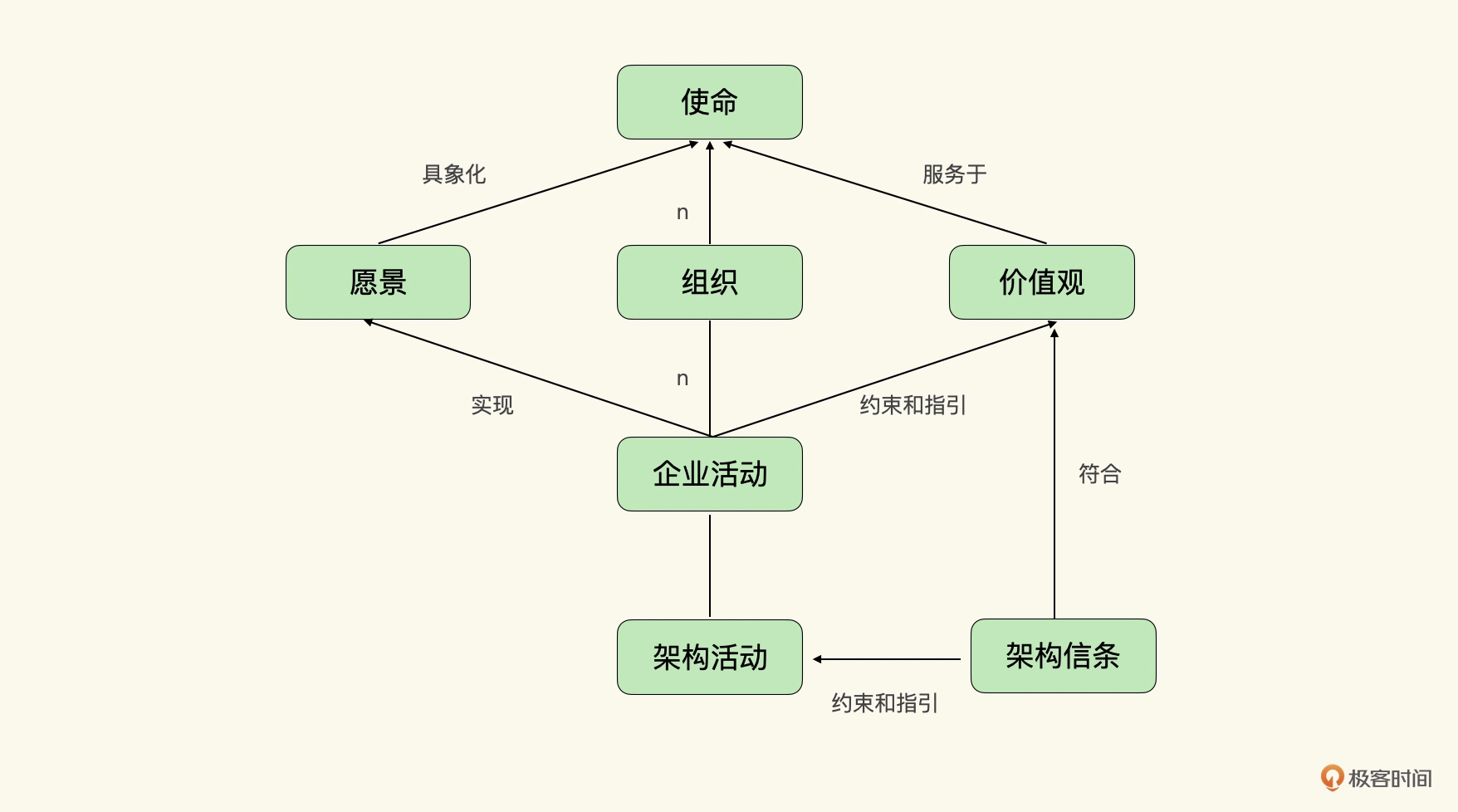
【郭东白架构课 模块二:创造价值】18|节点一:架构活动中为什么要做环境搭建?
你好,我是郭东白。在第 16、17 讲,我们讲解了架构师在架构活动中要起的作用,主要有达成共识、控制风险、保障交付和沉淀知识这四个方面。这是从架构师创造价值的维度来拆解的。 那么从这节课开始,我将从架构活动生命周期的维度上…...
15个awk的经典实战案例
目录 一、插入几个新字段 二、格式化个空白 三、筛选IPV4地址 命令及结果 第一种查询方式 第二种查询方式 第三种查询方式 四、读取.ini配置文件中的某段 命令及结果 第一种查询方式 第二种查询方式 五、根据某字段去重 命令及结果 第一种方式 第二种方式 六、…...
【JAVA】本地代码获取路径乱码
本地代码获取路径乱码 获取resources下资源乱码 解决方法: 获取路径后把返回值decode下就可以了. 用utf-8编码 String path this.getClass().getResource("").getPath();...
自然机器人最新发布:智能流程助手,与GPT深度融合
ChatGPT自2022年11月上线后就受到现象级地广泛关注,5天时间用户就已经突破百万,仅2个月时间月活用户就突破1亿,成为史上增速最快的消费级应用,远超TikTok、Facebook、Google等全球应用。它展现了类似人类的语言理解和对话交互能力…...

【Mybatis】4—动态SQL
⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/Code_Learning ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点个star~😊 如果文章对你有所帮助,可以点赞👍…...
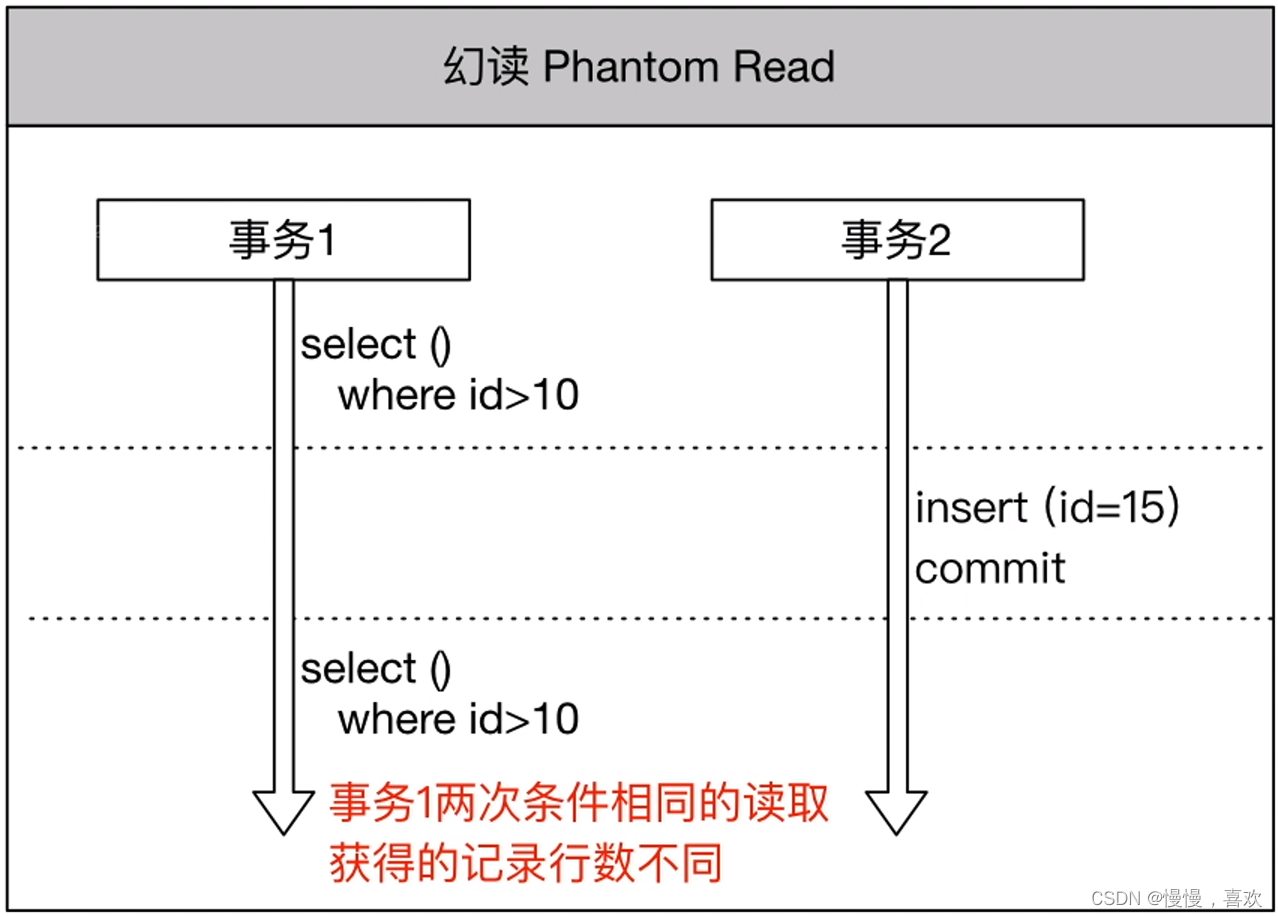
事务传播特性和隔离级别
事务的四大特性 1.原子性(Atomicity):事务不可再分,要么都执行,要么都不执行。 2.一致性(Consistency):事务执行前后,数据的完整性保持一致,即修改前后数据总…...
socket网络编程
端口 :主机上一个应用程序的代号(端口不变) 为什么不用PID来表示一个应用 因为PID会变化,而端口是不变的 套接字进程间通信——跨越主机 1、主机字节序列和网络字节序列 主机字节序列分为大端字节序和小端字节序,不同…...
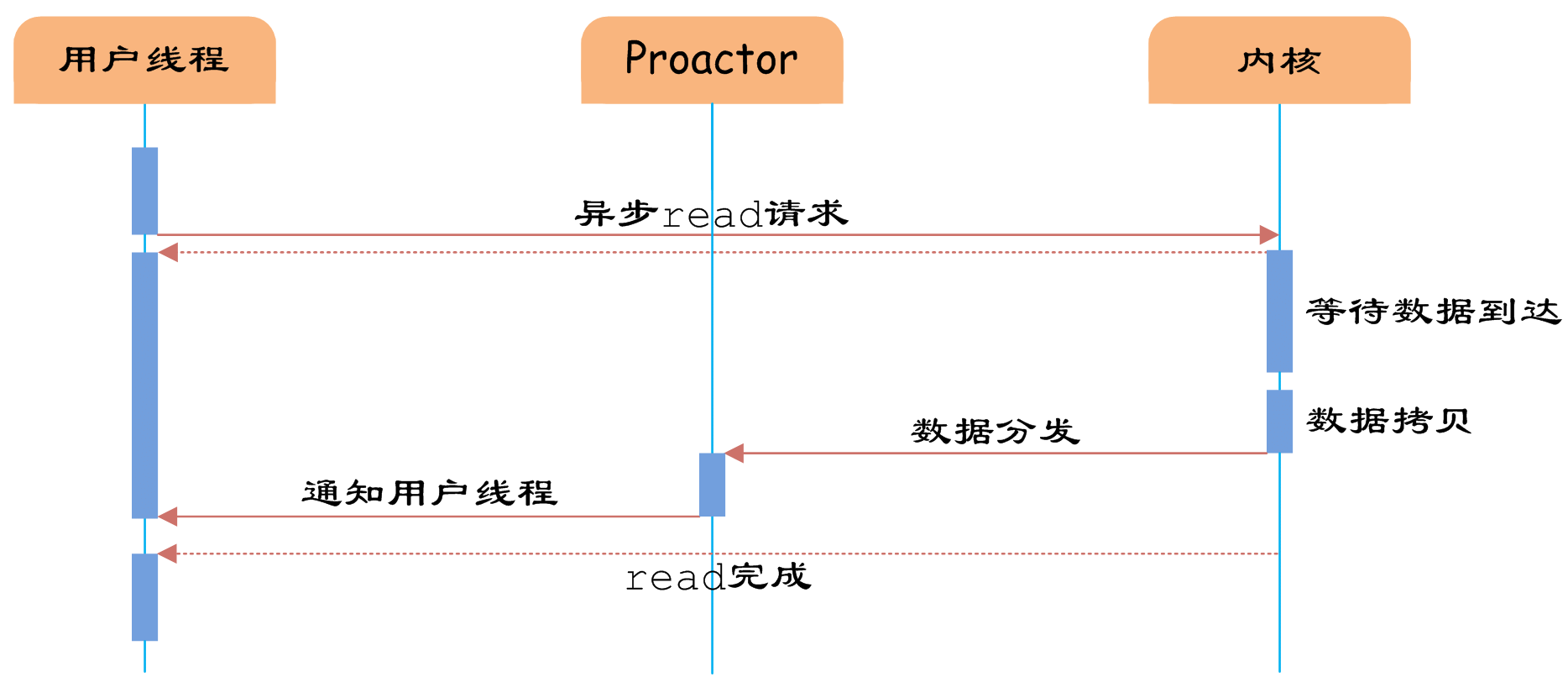
IO多路复用机制详解
高性能IO模型浅析 服务器端编程经常需要构造高性能的IO模型,常见的IO模型有四种: (1)同步阻塞IO(Blocking IO):即传统的IO模型。 (2)同步非阻塞IO(Non-blo…...

选择一款好用的营销项目管理可以更好帮您解决任何问题
营销项目管理软件哪个好用?使用Zoho Projects营销项目管理软件,您可以从营销活动中获得最佳结果,并获得可执行的见解。Zoho Projects的营销项目管理软件可让您和您的团队全面了解您的所有活动。监控您的社交渠道、跟踪结果并在一处进行交流。…...
第三章知识总结(期末复习可用))
计算机网络(第八版)第三章知识总结(期末复习可用)
本笔记来源于博主上课所记笔记整理,可能不全,欢迎大家批评指正,如果觉得有用记得点个赞,给博主点个关注...该笔记将会持续更新...整理不易,希望大家多多点赞。 第一章 第三章 数据链路层 数据链路层属于计算机网络的低…...
VScode配置8086汇编环境
目录 0、感慨 1、VScode的安装 2、下载MASM/TASM插件 3、测试汇编环境 新建文件 汇编文件配置 汇编代码的运行 0、感慨 搭配一个简单些的环境,对于我们汇编的学习很有帮助,在这里又不得不感叹vscode的强大,使用VScodeMASM/TASM插件就…...

银行数字化转型导师坚鹏:银行同业核心产品与营销策略解读
数字化背景下银行同业核心产品与营销策略解读课程背景: 数字化背景下,很多银行存在以下问题:不清楚银行同业核心产品发展现状?不清楚如何银行同业产品营销策略?不知道如何更好地挖掘他行优质客户? 课…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
