NumPy 秘籍中文第二版:二、高级索引和数组概念
原文:NumPy Cookbook - Second Edition
协议:CC BY-NC-SA 4.0
译者:飞龙
在本章中,我们将介绍以下秘籍:
- 安装 SciPy
- 安装 PIL
- 调整图像大小
- 比较视图和副本
- 翻转 Lena
- 花式索引
- 位置列表索引
- 布尔值索引
- 数独的步幅技巧
- 广播数组
简介
NumPy 以其高效的数组而闻名。 之所以成名,部分原因是索引容易。 我们将演示使用图像的高级索引技巧。 在深入研究索引之前,我们将安装必要的软件 – SciPy 和 PIL。 如果您认为有此需要,请参阅第 1 章“使用 IPython”的“安装 matplotlib”秘籍。
在本章和其他章中,我们将使用以下导入:
import numpy as np
import matplotlib.pyplot as plt
import scipy
我们还将尽可能为print() Python 函数使用最新的语法。
注意
Python2 是仍然很流行的主要 Python 版本,但与 Python3 不兼容。Python2 直到 2020 年才正式失去支持。主要区别之一是print()函数的语法。 本书使用的代码尽可能与 Python2 和 Python3 兼容。
本章中的一些示例涉及图像处理。 为此,我们将需要 Python 图像库(PIL),但不要担心; 必要时会在本章中提供帮助您安装 PIL 和其他必要 Python 软件的说明和指示。
安装 SciPy
SciPy 是科学的 Python 库,与 NumPy 密切相关。 实际上,SciPy 和 NumPy 在很多年前曾经是同一项目。 就像 NumPy 一样,SciPy 是一个开放源代码项目,已获得 BSD 许可。 在此秘籍中,我们将安装 SciPy。 SciPy 提供高级功能,包括统计,信号处理,线性代数,优化,FFT,ODE 求解器,插值,特殊功能和积分。 NumPy 有一些重叠,但是 NumPy 主要提供数组功能。
准备
在第 1 章,“使用 IPython”中,我们讨论了如何安装setuptools和pip。 如有必要,请重新阅读秘籍。
操作步骤
在此秘籍中,我们将完成安装 SciPy 的步骤:
-
从源安装:如果已安装 Git,则可以使用以下命令克隆 SciPy 存储库:
$ git clone https://github.com/scipy/scipy.git$ python setup.py build $ python setup.py install --user这会将 SciPy 安装到您的主目录。 它需要 Python 2.6 或更高版本。
在构建之前,您还需要安装 SciPy 依赖的以下包:
BLAS和LAPACK库- C 和 Fortran 编译器
您可能已经在 NumPy 安装过程中安装了此软件。
-
在 Linux 上安装 SciPy:大多数 Linux 发行版都包含 SciPy 包。 我们将遵循一些流行的 Linux 发行版中的必要步骤(您可能需要以 root 用户身份登录或具有
sudo权限):-
为了在 RedHat,Fedora 和 CentOS 上安装 SciPy,请从命令行运行以下指令:
$ yum install python-scipy -
为了在 Mandriva 上安装 SciPy,请运行以下命令行指令:
$ urpmi python-scipy -
为了在 Gentoo 上安装 SciPy,请运行以下命令行指令:
$ sudo emerge scipy -
在 Debian 或 Ubuntu 上,我们需要输入以下指令:
$ sudo apt-get install python-scipy
-
-
在 MacOSX 上安装 SciPy:需要 Apple Developer Tools(XCode),因为它包含
BLAS和LAPACK库。 可以在 App Store 或 Mac 随附的安装 DVD 中找到它。 或者您可以从 Apple Developer 的连接网站获取最新版本。 确保已安装所有内容,包括所有可选包。您可能已经为 NumPy 安装了 Fortran 编译器。
gfortran的二进制文件可以在这个链接中找到。 -
使用
easy_install或pip安装 SciPy:您可以使用以下两个命令中的任何一个来安装 SciPy(sudo的需要取决于权限):$ [sudo] pip install scipy $ [sudo] easy_install scipy```** -
在 Windows 上安装:如果已经安装 Python,则首选方法是下载并使用二进制发行版。 或者,您可以安装 Anaconda 或 Enthought Python 发行版,该发行版与其他科学 Python 包一起提供。
-
检查安装:使用以下代码检查 SciPy 安装:
import scipy print(scipy.__version__) print(scipy.__file__)这应该打印正确的 SciPy 版本。
工作原理
大多数包管理器都会为您解决依赖项(如果有)。 但是,在某些情况下,您需要手动安装它们。 这超出了本书的范围。
另见
如果遇到问题,可以在以下位置寻求帮助:
freenode的#scipyIRC 频道- SciPy 邮件列表
安装 PIL
PIL(Python 图像库)是本章中进行图像处理的先决条件。 如果愿意,可以安装 Pillow,它是 PIL 的分支。 有些人喜欢 Pillow API; 但是,我们不会在本书中介绍其安装。
操作步骤
让我们看看如何安装 PIL:
-
在 Windows 上安装 PIL:使用 Windows 中的 PIL 可执行文件安装 PIL。
-
在 Debian 或 Ubuntu 上安装:在 Debian 或 Ubuntu 上,使用以下命令安装 PIL:
$ sudo apt-get install python-imaging -
使用
easy_install或pip安装:在编写本书时,似乎 RedHat,Fedora 和 CentOS 的包管理器没有对 PIL 的直接支持。 因此,如果您使用的是这些 Linux 发行版之一,请执行此步骤。使用以下任一命令安装 :
$ easy_install PIL $ sudo pip install PIL
另见
- 可在这里 找到有关 PILLOW(PIL 的分支)的说明。
调整图像大小
在此秘籍中,我们将把 Lena 的样例图像(在 SciPy 发行版中可用)加载到数组中。 顺便说一下,本章不是关于图像操作的。 我们将只使用图像数据作为输入。
注意
Lena Soderberg 出现在 1972 年的《花花公子》杂志中。 由于历史原因,这些图像之一经常用于图像处理领域。 不用担心,该图像完全可以安全工作。
我们将使用repeat()函数调整图像大小。 此函数重复一个数组,这意味着在我们的用例中按一定的大小调整图像大小。
准备
此秘籍的前提条件是必须安装 SciPy,matplotlib 和 PIL。 看看本章和第 1 章,“使用 IPython”的相应秘籍。
操作步骤
通过以下步骤调整图像大小:
-
首先,导入
SciPy。 SciPy 具有lena()函数。 它用于将图像加载到 NumPy 数组中:lena = scipy.misc.lena()从 0.10 版本开始发生了一些重构,因此,如果您使用的是旧版本,则正确的代码如下:
lena = scipy.lena() -
使用
numpy.testing包中的assert_equal()函数检查 Lena 数组的形状-这是可选的完整性检查测试:np.testing.assert_equal((LENA_X, LENA_Y), lena.shape) -
使用
repeat()函数调整 Lena 数组的大小。 我们在x和y方向上给此函数一个调整大小的因子:resized = lena.repeat(yfactor, axis=0).repeat(xfactor, axis=1) -
我们将在同一网格的两个子图中绘制 Lena 图像和调整大小后的图像。 使用以下代码在子图中绘制 Lena 数组:
plt.subplot(211) plt.title("Lena") plt.axis("off") plt.imshow(lena)matplotlib
subplot()函数创建一个子图。 此函数接受一个三位整数作为参数,其中第一位是行数,第二位是列数,最后一位是子图的索引,从 1 开始。imshow()函数显示图像。 最后,show()函数显示最终结果。将调整大小后的数组绘制在另一个子图中并显示它。 索引现在为 2:
plt.subplot(212) plt.title("Resized") plt.axis("off") plt.imshow(resized) plt.show()以下屏幕截图显示了结果,以及原始图像(第一幅)和调整大小后的图像(第二幅):
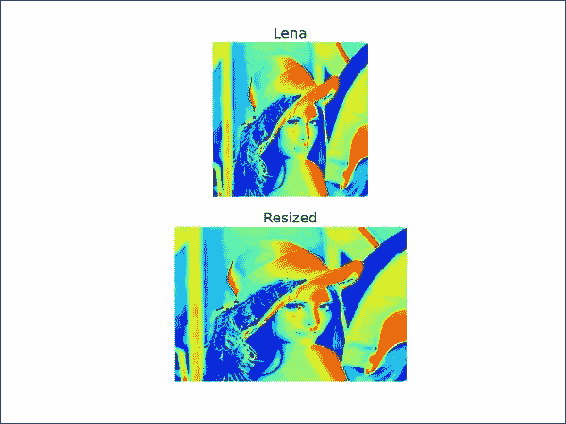
以下是本书代码包中
resize_lena.py文件中该秘籍的完整代码:import scipy.misc import matplotlib.pyplot as plt import numpy as np# This script resizes the Lena image from Scipy.# Loads the Lena image into an array lena = scipy.misc.lena()#Lena's dimensions LENA_X = 512 LENA_Y = 512#Check the shape of the Lena array np.testing.assert_equal((LENA_X, LENA_Y), lena.shape)# Set the resize factors yfactor = 2 xfactor = 3# Resize the Lena array resized = lena.repeat(yfactor, axis=0).repeat(xfactor, axis=1)#Check the shape of the resized array np.testing.assert_equal((yfactor * LENA_Y, xfactor * LENA_Y), resized.shape)# Plot the Lena array plt.subplot(211) plt.title("Lena") plt.axis("off") plt.imshow(lena)#Plot the resized array plt.subplot(212) plt.title("Resized") plt.axis("off") plt.imshow(resized) plt.show()
工作原理
repeat()函数重复数组,在这种情况下,这会导致原始图像的大小改变。 subplot() matplotlib 函数创建一个子图。 imshow()函数显示图像。 最后,show()函数显示最终结果。
另见
- 第 1 章“使用 IPython”中的“安装 matplotlib”
- 本章中的“安装 SciPy”
- 本章中的“安装 PIL”
- 这个页面中介绍了
repeat()函数。
创建视图和副本
了解何时处理共享数组视图以及何时具有数组数据的副本,这一点很重要。 例如,切片将创建一个视图。 这意味着,如果您将切片分配给变量,然后更改基础数组,则此变量的值将更改。 我们将根据著名的 Lena 图像创建一个数组,复制该数组,创建一个视图,最后修改视图。
准备
前提条件与先前的秘籍相同。
操作步骤
让我们创建 Lena 数组的副本和视图:
-
创建 Lena 数组的副本:
acopy = lena.copy() -
创建数组的视图:
aview = lena.view() -
使用
flat迭代器将视图的所有值设置为0:aview.flat = 0最终结果是只有一个图像(与副本相关的图像)显示了花花公子模型。 其他图像完全消失:
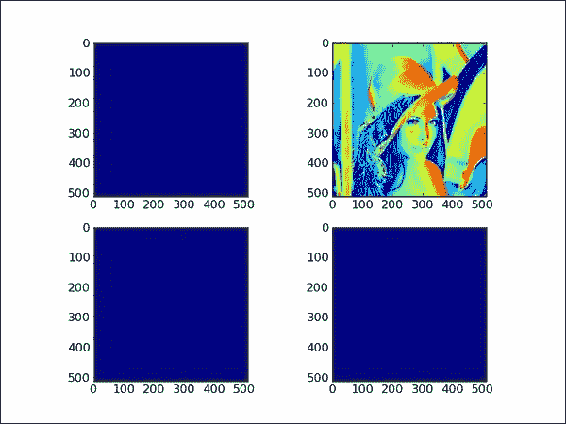
以下是本教程的代码,显示了本书代码包中
copy_view.py文件中数组视图和副本的行为:import scipy.misc import matplotlib.pyplot as pltlena = scipy.misc.lena() acopy = lena.copy() aview = lena.view()# Plot the Lena array plt.subplot(221) plt.imshow(lena)#Plot the copy plt.subplot(222) plt.imshow(acopy)#Plot the view plt.subplot(223) plt.imshow(aview)# Plot the view after changes aview.flat = 0 plt.subplot(224) plt.imshow(aview)plt.show()
工作原理
如您所见,通过在程序结尾处更改视图,我们更改了原始 Lena 数组。 这样就产生了三张蓝色(如果您正在查看黑白图像,则为空白)图像-复制的数组不受影响。 重要的是要记住,视图不是只读的。
另见
- NumPy
view()函数的文档位于这里
翻转 Lena
我们将翻转 SciPy Lena 图像-当然,所有这些都是以科学的名义,或者至少是作为演示。 除了翻转图像,我们还将对其进行切片并对其应用遮罩。
操作步骤
步骤如下:
-
使用以下代码围绕垂直轴翻转 Lena 数组:
plt.imshow(lena[:,::-1]) -
从图像中切出一部分并将其绘制出来。 在这一步中,我们将看一下 Lena 数组的形状。 该形状是表示数组大小的元组。 以下代码有效地选择了花花公子图片的左上象限:
plt.imshow(lena[:lena.shape[0]/2,:lena.shape[1]/2]) -
通过在 Lena 数组中找到所有偶数的值,对图像应用遮罩(这对于演示目的来说是任意的)。 复制数组并将偶数值更改为 0。 这样会在图像上放置很多蓝点(如果您正在查看黑白图像,则会出现暗点):
mask = lena % 2 == 0 masked_lena = lena.copy() masked_lena[mask] = 0所有这些工作都会产生
2 x 2的图像网格,如以下屏幕截图所示:
这是本书代码包中
flip_lena.py文件中此秘籍的完整代码:import scipy.misc import matplotlib.pyplot as plt# Load the Lena array lena = scipy.misc.lena()# Plot the Lena array plt.subplot(221) plt.title('Original') plt.axis('off') plt.imshow(lena)#Plot the flipped array plt.subplot(222) plt.title('Flipped') plt.axis('off') plt.imshow(lena[:,::-1])#Plot a slice array plt.subplot(223) plt.title('Sliced') plt.axis('off') plt.imshow(lena[:lena.shape[0]/2,:lena.shape[1]/2])# Apply a mask mask = lena % 2 == 0 masked_lena = lena.copy() masked_lena[mask] = 0 plt.subplot(224) plt.title('Masked') plt.axis('off') plt.imshow(masked_lena)plt.show()
另见
- 第 1 章“使用 IPython”中的“安装 matplotlib”
- 本章中的“安装 SciPy”
- 本章中的“安装 PIL”
花式索引
在本教程中,我们将应用花式索引将 Lena 图像的对角线值设置为 0。这将沿着对角线绘制黑线并交叉,这不是因为图像有问题,而仅仅作为练习。 花式索引是不涉及整数或切片的索引; 这是正常的索引编制。
操作步骤
我们将从第一个对角线开始:
-
将第一个对角线的值设置为
0。要将对角线值设置为
0,我们需要为x和y值定义两个不同的范围:lena[range(xmax), range(ymax)] = 0 -
将另一个对角线的值设置为
0。要设置另一个对角线的值,我们需要一组不同的范围,但是原理保持不变:
lena[range(xmax-1,-1,-1), range(ymax)] = 0最后,我们得到带有对角线标记的图像,如以下屏幕截图所示:
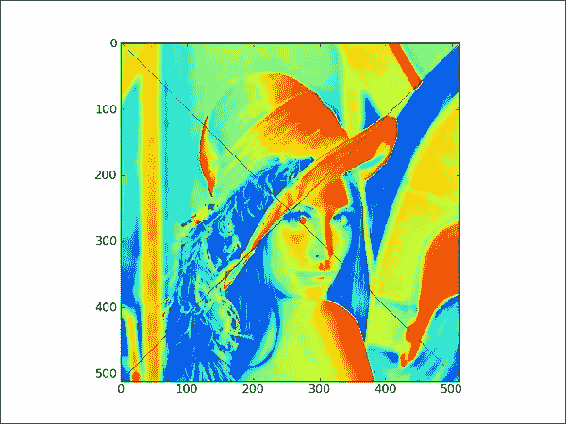
以下是本书代码集中
fancy.py文件中该秘籍的完整代码:import scipy.misc import matplotlib.pyplot as plt# This script demonstrates fancy indexing by setting values # on the diagonals to 0.# Load the Lena array lena = scipy.misc.lena() xmax = lena.shape[0] ymax = lena.shape[1]# Fancy indexing # Set values on diagonal to 0 # x 0-xmax # y 0-ymax lena[range(xmax), range(ymax)] = 0# Set values on other diagonal to 0 # x xmax-0 # y 0-ymax lena[range(xmax-1,-1,-1), range(ymax)] = 0# Plot Lena with diagonal lines set to 0 plt.imshow(lena) plt.show()
工作原理
我们为x值和y值定义了单独的范围。 这些范围用于索引 Lena 数组。 花式索引是基于内部 NumPy 迭代器对象执行的。 执行以下步骤:
- 创建迭代器对象。
- 迭代器对象绑定到数组。
- 数组元素通过迭代器访问。
另见
- 花式索引的实现文档
位置列表索引
让我们使用ix_()函数来随机播放 Lena 图像。 此函数根据多个序列创建网格。
操作步骤
我们将从随机改组数组索引开始:
-
使用
numpy.random模块的shuffle()函数创建随机索引数组:def shuffle_indices(size):arr = np.arange(size)np.random.shuffle(arr)return arr -
绘制乱序的索引:
plt.imshow(lena[np.ix_(xindices, yindices)])我们得到的是一张完全打乱的 Lena 图像,如以下屏幕截图所示:
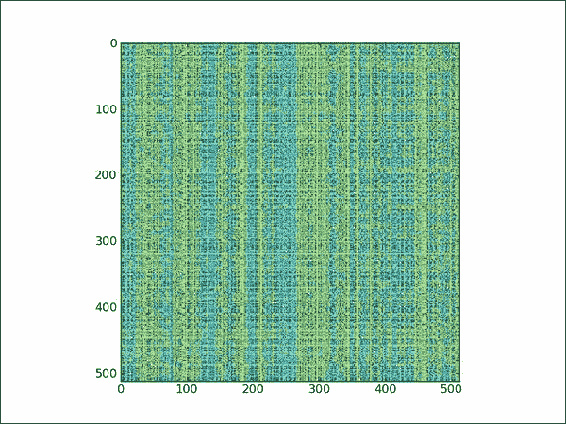
这是本书代码包中
ix.py文件中秘籍的完整代码:import scipy.misc import matplotlib.pyplot as plt import numpy as np# Load the Lena array lena = scipy.misc.lena() xmax = lena.shape[0] ymax = lena.shape[1]def shuffle_indices(size):'''Shuffles an array with values 0 - size'''arr = np.arange(size)np.random.shuffle(arr)return arrxindices = shuffle_indices(xmax) np.testing.assert_equal(len(xindices), xmax) yindices = shuffle_indices(ymax) np.testing.assert_equal(len(yindices), ymax)# Plot Lena plt.imshow(lena[np.ix_(xindices, yindices)]) plt.show()
另见
ix_()函数的文档页面
布尔值索引
布尔索引是基于布尔数组的索引 ,属于奇特索引的类别。
操作步骤
我们将这种索引技术应用于图像:
-
在对角线上带有点的图像。
这在某种程度上类似于本章中的“花式索引”秘籍。 这次,我们在图像的对角线上选择模
4:def get_indices(size):arr = np.arange(size)return arr % 4 == 0然后,我们只需应用此选择并绘制点:
lena1 = lena.copy() xindices = get_indices(lena.shape[0]) yindices = get_indices(lena.shape[1]) lena1[xindices, yindices] = 0 plt.subplot(211) plt.imshow(lena1) -
在最大值的四分之一到四分之三之间选择数组值,并将它们设置为
0:lena2[(lena > lena.max()/4) & (lena < 3 * lena.max()/4)] = 0带有两个新图像的图看起来类似于以下屏幕截图所示:
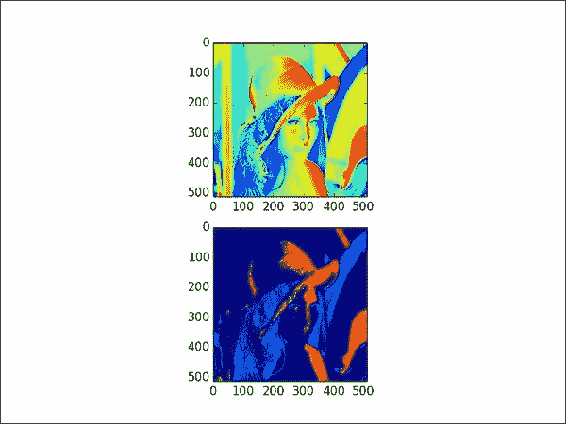
这是本书代码包中
boolean_indexing.py文件中该秘籍的完整代码:import scipy.misc import matplotlib.pyplot as plt import numpy as np# Load the Lena array lena = scipy.misc.lena()def get_indices(size):arr = np.arange(size)return arr % 4 == 0# Plot Lena lena1 = lena.copy() xindices = get_indices(lena.shape[0]) yindices = get_indices(lena.shape[1]) lena1[xindices, yindices] = 0 plt.subplot(211) plt.imshow(lena1)lena2 = lena.copy() # Between quarter and 3 quarters of the max value lena2[(lena > lena.max()/4) & (lena < 3 * lena.max()/4)] = 0 plt.subplot(212) plt.imshow(lena2)plt.show()
工作原理
由于布尔值索引是一种花式索引,因此它的工作方式基本相同。 这意味着索引是在特殊的迭代器对象的帮助下发生的。
另见
- “花式索引”
数独的步幅技巧
ndarray 类具有strides字段,它是一个元组,指示通过数组时要在每个维中步进的字节数。 让我们对将数独谜题拆分为3 x 3正方形的问题应用一些大步技巧。
注意
对数独的规则进行解释超出了本书的范围。 简而言之,数独谜题由3 x 3的正方形组成。 这些正方形均包含九个数字。 有关更多信息,请参见这里。
操作步骤
应用如下的跨步技巧:
-
让我们定义
sudoku数组。 此数组充满了一个实际的已解决的数独难题的内容:sudoku = np.array([[2, 8, 7, 1, 6, 5, 9, 4, 3],[9, 5, 4, 7, 3, 2, 1, 6, 8],[6, 1, 3, 8, 4, 9, 7, 5, 2],[8, 7, 9, 6, 5, 1, 2, 3, 4],[4, 2, 1, 3, 9, 8, 6, 7, 5],[3, 6, 5, 4, 2, 7, 8, 9, 1],[1, 9, 8, 5, 7, 3, 4, 2, 6],[5, 4, 2, 9, 1, 6, 3, 8, 7],[7, 3, 6, 2, 8, 4, 5, 1, 9]]) -
ndarray的itemsize字段为我们提供了数组中的字节数。 给定itemsize,请计算步幅:strides = sudoku.itemsize * np.array([27, 3, 9, 1]) -
现在我们可以使用
np.lib.stride_tricks模块的as_strided()函数将拼图分解成正方形:squares = np.lib.stride_tricks.as_strided(sudoku, shape=shape, strides=strides) print(squares)该代码打印单独的数独正方形,如下所示:
[[[[2 8 7][9 5 4][6 1 3]][[1 6 5][7 3 2][8 4 9]][[9 4 3][1 6 8][7 5 2]]][[[8 7 9][4 2 1][3 6 5]][[6 5 1][3 9 8][4 2 7]][[2 3 4][6 7 5][8 9 1]]][[[1 9 8][5 4 2][7 3 6]][[5 7 3][9 1 6][2 8 4]][[4 2 6][3 8 7][5 1 9]]]]以下是本书代码包中
strides.py文件中此秘籍的完整源代码:import numpy as npsudoku = np.array([[2, 8, 7, 1, 6, 5, 9, 4, 3],[9, 5, 4, 7, 3, 2, 1, 6, 8],[6, 1, 3, 8, 4, 9, 7, 5, 2],[8, 7, 9, 6, 5, 1, 2, 3, 4],[4, 2, 1, 3, 9, 8, 6, 7, 5],[3, 6, 5, 4, 2, 7, 8, 9, 1],[1, 9, 8, 5, 7, 3, 4, 2, 6],[5, 4, 2, 9, 1, 6, 3, 8, 7],[7, 3, 6, 2, 8, 4, 5, 1, 9]])shape = (3, 3, 3, 3)strides = sudoku.itemsize * np.array([27, 3, 9, 1])squares = np.lib.stride_tricks.as_strided(sudoku, shape=shape, strides=strides) print(squares)
工作原理
我们应用了跨步技巧,将数独谜题拆分为3 x 3的正方形。 步幅告诉我们通过数独数组时每一步需要跳过的字节数。
另见
strides属性的文档在这里
广播数组
在不知道的情况下,您可能已经广播了数组。 简而言之,即使操作数的形状不同,NumPy 也会尝试执行操作。 在此秘籍中,我们将一个数组和一个标量相乘。 标量被扩展为数组操作数的形状,然后执行乘法。 我们将下载一个音频文件并制作一个更安静的新版本。
操作步骤
让我们从读取 WAV 文件开始:
-
我们将使用标准的 Python 代码下载 Austin Powers 的音频文件。 SciPy 具有 WAV 文件模块,可让您加载声音数据或生成 WAV 文件。 如果已安装 SciPy,则我们应该已经有此模块。
read()函数返回data数组和采样率。 在此示例中,我们仅关心数据:sample_rate, data = scipy.io.wavfile.read(WAV_FILE) -
使用 matplotlib 绘制原始 WAV 数据。 将子图命名为
Original:plt.subplot(2, 1, 1) plt.title("Original") plt.plot(data) -
现在,我们将使用 NumPy 制作更安静的音频样本。 这只是通过与常量相乘来创建具有较小值的新数组的问题。 这就是广播魔术发生的地方。 最后,由于 WAV 格式,我们需要确保与原始数组具有相同的数据类型:
newdata = data * 0.2 newdata = newdata.astype(np.uint8) -
可以将新数组写入新的 WAV 文件,如下所示:
scipy.io.wavfile.write("quiet.wav",sample_rate, newdata) -
使用 matplotlib 绘制新数据数组:
plt.subplot(2, 1, 2) plt.title("Quiet") plt.plot(newdata)plt.show()结果是原始 WAV 文件数据和具有较小值的新数组的图,如以下屏幕快照所示:
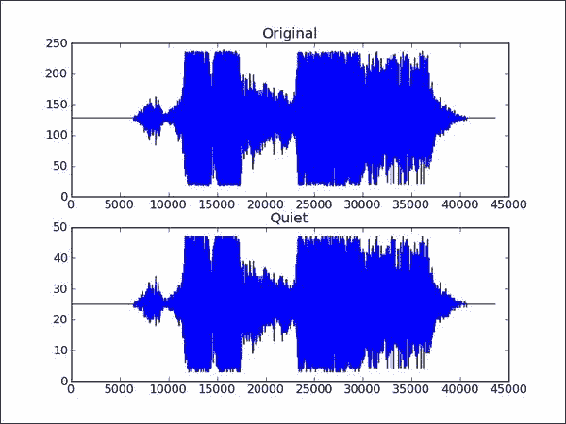
这是本书代码包中
broadcasting.py文件中该秘籍的完整代码:import scipy.io.wavfile import matplotlib.pyplot as plt import urllib2 import numpy as np# Download audio file response = urllib2.urlopen('http://www.thesoundarchive.com/austinpowers/smashingbaby.wav') print(response.info()) WAV_FILE = 'smashingbaby.wav' filehandle = open(WAV_FILE, 'w') filehandle.write(response.read()) filehandle.close() sample_rate, data = scipy.io.wavfile.read(WAV_FILE) print("Data type", data.dtype, "Shape", data.shape)# Plot values original audio plt.subplot(2, 1, 1) plt.title("Original") plt.plot(data)# Create quieter audio newdata = data * 0.2 newdata = newdata.astype(np.uint8) print("Data type", newdata.dtype, "Shape", newdata.shape)# Save quieter audio file scipy.io.wavfile.write("quiet.wav",sample_rate, newdata)# Plot values quieter file plt.subplot(2, 1, 2) plt.title("Quiet") plt.plot(newdata)plt.show()
另见
以下链接提供了更多背景信息:
scipy.io.read()函数scipy.io.write()函数- 在这个链接中解释了广播概念。
相关文章:

NumPy 秘籍中文第二版:二、高级索引和数组概念
原文:NumPy Cookbook - Second Edition 协议:CC BY-NC-SA 4.0 译者:飞龙 在本章中,我们将介绍以下秘籍: 安装 SciPy安装 PIL调整图像大小比较视图和副本翻转 Lena花式索引位置列表索引布尔值索引数独的步幅技巧广播数…...

新品-图灵超频工作站GT430M介绍
曾经历史 UltraLAB GTxxxM系列是西安坤隆公司专注于超频高速计算应用的图形工作站。 2008年 获取排名第一、二的中国象棋软件均采用该机型。 2019年 推出采用Intel 超频Xeon(28核4.8GHz)显著提升电磁仿真频域算法求解、第一个解决8K视频解码与渲染。 今…...

js时间格式化精确到毫秒
/*** 数字前置补零* param value 值* param length 位数* returns {string}*/ export function digit(value, length 2) {if (typeof value "undefined" ||value null ||String(value).length > length) {return value;}return (Array(length).join("0&qu…...

QT样式表详解
本文详细介绍qt的样式表,包含样式表如何使用,常见语句和选择器。 背景说明 样式表用于设置外观,他是设置控件外观的方式之一。其他方式如下: 控件的成员函数,如QWidget::setBackground样式表调色板 优先级依次提高…...

最值得入手的好物有哪些,推荐几款实用的数码好物
随着科技的进步,越来越多的数码产品不断的出现在我们的生活中,这其中也不乏一些实用的数码产品,让我们可以享受更舒适的生活,提高我们的工作效率。下面就给大家分享几款我最近使用过的一些数码产品,它们不仅功能强大而…...
【20230407】NVIDIA显卡算力、Jetson比较
1 基本概念 1.1 算力单位 TOPS:指的是每秒钟可以执行的整数运算次数,它代表着计算机在处理图像、音频等任务时的处理能力。TOPS的单位是万亿次每秒(trillion operations per second)。一般是指整数运算能力INT8。 TFLOPS&#…...

dsl语法
查询 1.查询所有(默认有分页查询) #查询所有 GET /hotel/_search {"query": {"match_all": {}} } 2.match查询(条件查询)-----包含四川和外滩的信息,信息匹配度越高越靠前,两者存在一…...
不让CPU偷懒
文章资料摘自——《程序员的自我修养》 为了防止cpu执行完该程序后需要等待程序员手动加入下一个程序,才可以继续运行,这里大大浪费了cpu的效率,要知道cpu是十分昂贵的。 多道程序 在计算机发展的早期,CPU使用十分不方便&#x…...
动力节点王鹤SpringBoot3笔记——第七章 视图技术Thymeleaf
目录 第七章 视图技术Thymeleaf 前言 7.1 表达式 7.2 if-for 第七章 视图技术Thymeleaf 前言 Thymeleaf 是一个表现层的模板引擎, 一般被使用在 Web 环境中,它可以处理 HTML, XML、 JS 等文档,简单来说,它可以将 JSP 作…...

从比特保存和信息保存看数字资源长期保存
引用IBM以色列海法实验室的观点,数字资源长期保存包含两个层面含义,即比特保存与信息保存。也就是说,要实现数字资源的长期保存,必须同时做到比特保存和信息保存。 一 概念 01 比特保存,也叫物理保存,主…...

兰伯特光照模型(Lambert Lighting)和半兰伯特光照模型(Half-Lanbert)
关于漫反射 光打到凹凸不平的平面上,光线会被反射到四面八方,被称为漫反射 关于这种模型,由于光线由于分散,所以进入人眼的光线强度和观察角度没有区别 在A点和B点接收到的光线强度是一样的 在漫反射下,光线强度只和光…...
Python 进阶指南(编程轻松进阶):二、环境配置和命令行
原文:http://inventwithpython.com/beyond/chapter2.html 环境配置是配置你的计算机环境,以便你写代码的过程。这包括安装任何必要的工具,配置它们,以及处理安装过程中的任何问题。没有一键配置这种傻瓜式操作过程,因为…...

求职半年,三月成功拿到阿里offer,分享一波面经...
前言 不论是校招还是社招都避免不了各种⾯试、笔试,如何去准备这些东⻄就显得格外重要。不论是笔试还是⾯试都是有章可循的,我这个“有章可循”说的意思只是说应对技术⾯试是可以提前准备,所谓不打无准备的仗就是这个道理。 以下为大家&…...

餐饮店的运营需要考虑哪些方面
餐饮店的运营需要多方面的考虑和规划,以下是传递宝APP上一些常用的餐饮店运营方法: 1.定位:明确餐饮店的定位和目标客户群体,针对不同的客户需求,提供个性化的服务和产品,比如是附近的上班族,还…...

Multi-modal Alignment using Representation Codebook
Multi-modal Alignment using Representation Codebook 题目Multi-modal Alignment using Representation Codebook译题使用表示代码集的多模态对齐期刊/会议CVPR 摘要:对齐来自不同模态的信号是视觉语言表征学习(representation learning)的…...

关于vector的emplace_back和push_back的区别
实验代码: class A { public:A(int x) {x x;cout << "construct A" << endl;}A(const A& a) {x a.x;cout << "copy construct A" << endl;}A(const A&& a) {cout << "Move construct A"…...

Vue——表单输入绑定
目录 基本用法 文本 多行文本 复选框 选择器 值绑定 复选框 单选按钮 选择器选项 修饰符 .lazy .number .trim 组件上的 v-model 在前端处理表单时,我们常常需要将表单输入框的内容同步给 JavaScript 中相应的变量。手动连接值绑定…...
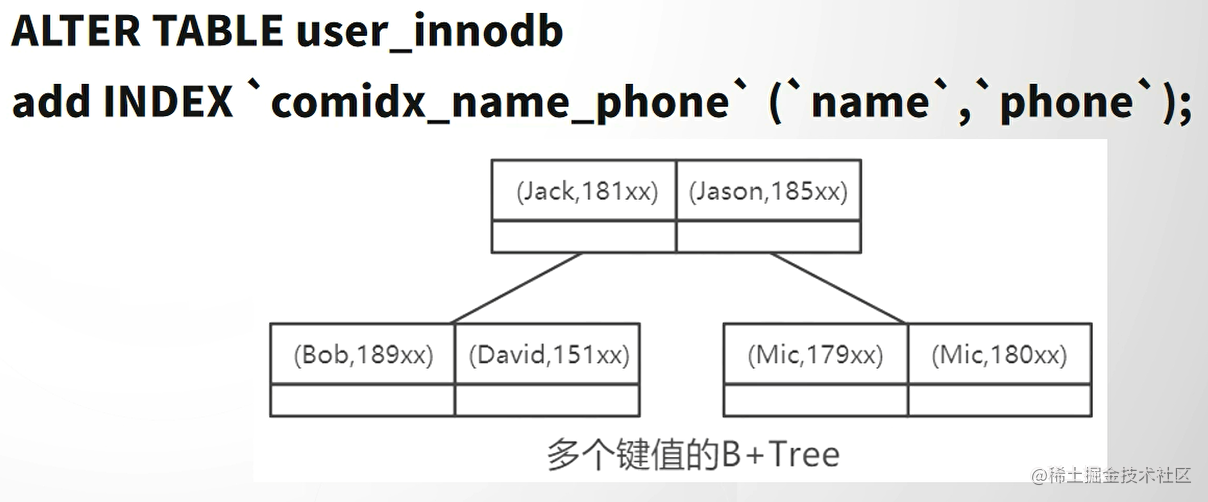
MySQL性能优化(二)索引
文章目录优化手段准备案例索引的本质索引的数据结构不同存储引擎中索引的实践MyIsam (索引没有主次之分、都存放在MYI文件)主键索引其他索引InnoDB(数据即索引、索引即数据)主键索引——聚集索引聚集索引其他索引没有主键的情况&a…...
< 每日闲谈:你真的了解 “ ChatGPT ” 嘛 ? >
< 每日闲谈:你真的了解 “ ChatGPT ” 嘛 ? >👉 前言👉 OpenAI的创立👉 ChatGPT有何过人之处?> 效果演示👉 OpenAI看家之作 — GPT自然语言模型> GPT发展史> 里程碑-GPT3> 从…...
改善Instagram客户服务的6个技巧
Instagram仍然是全球前四大社交网络,按用户数量排名。它通过其创新的过滤器、内容创建工具、视频和卷轴选项继续增长并推动流量。这是一个平台,世界顶级名人和有影响力的人可以为全球用户提供有趣和令人印象深刻的内容。 但不仅仅是一个娱乐平台…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
