当前位置： 首页 > news >正文

兰伯特光照模型(Lambert Lighting)和半兰伯特光照模型（Half-Lanbert）

news 2026/2/11 2:39:30

关于漫反射

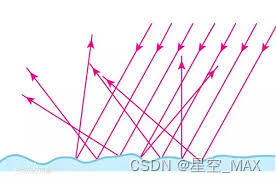
光打到凹凸不平的平面上，光线会被反射到四面八方，被称为漫反射

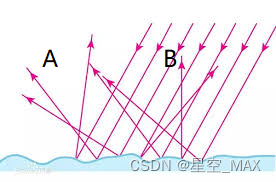
 关于这种模型，由于光线由于分散，所以进入人眼的光线强度和观察角度没有区别

 在A点和B点接收到的光线强度是一样的

在漫反射下，光线强度只和光的入射角度有关

关于法线和叉乘

法线，是指始终垂直于某平面的虚线，这是在二维平面下的法线

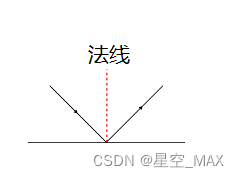
叉乘是求一条垂直于平面的向量

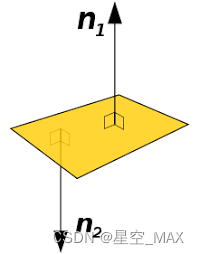
 可以用叉乘求出物体的法线

关于点乘

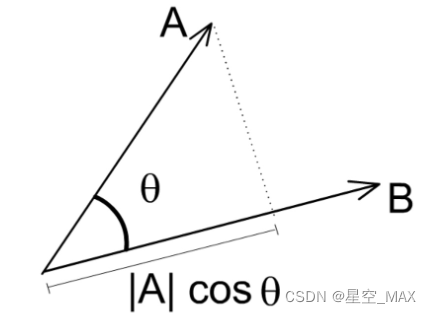
点乘表示A在B方向上的投影与B方向的乘机，反映了两个向量在方向上的相似度

计算公式为：

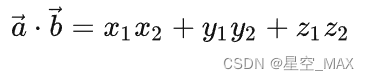
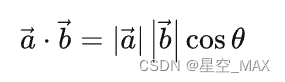
兰伯特光照模型(Lambert Lighting)

diffuse = I*cosθ

其中I为入射光强度

cosθ为光源方向和顶点法线的余弦，也就是两者的点乘，这个值越大，则cosθ越大

但是如果光在物体背面，则这个值为负数，于是就归为0就可以了

然后再乘上材质的颜色就是最后的颜色值了，也就是下面的完全公式

Diffuse = 直射光颜色 *材质颜色 * max(0,cos夹角(光和法线的夹角))

在辐射度量学之前，图形学一直处于一个想当然的境地

这个公式是在1760年提出来的，这个公式完全是经验公式，看起来像那么回事就可以了

但是兰伯特光照模型有个弊端，就是在物体打不着光的一面完全是黑色的，会“不那么好看”

于是就有了半兰伯特光照模型

半兰伯特光照模型（Half-Lanbert）

在1998的《半条命》的游戏引擎中，提出了半兰伯特的光照模型

在半兰伯特光照模型公式中

Diffuse = 直射光颜色 * 材质颜色 * (dot(光源方向, 法线方向) * 0.5 + 0.5)

在光在物体的背面的时候，最后的计算结果也会有明暗变化

这样物体就会”好看多了“

相关文章：

兰伯特光照模型(Lambert Lighting)和半兰伯特光照模型（Half-Lanbert）

关于漫反射 光打到凹凸不平的平面上，光线会被反射到四面八方，被称为漫反射 关于这种模型，由于光线由于分散，所以进入人眼的光线强度和观察角度没有区别 在A点和B点接收到的光线强度是一样的 在漫反射下，光线强度只和光…...

编程日记 2023/4/14 7:07:39

Python 进阶指南（编程轻松进阶）：二、环境配置和命令行

原文：http://inventwithpython.com/beyond/chapter2.html 环境配置是配置你的计算机环境，以便你写代码的过程。这包括安装任何必要的工具，配置它们，以及处理安装过程中的任何问题。没有一键配置这种傻瓜式操作过程，因为…...

编程日记 2023/4/14 7:02:38

求职半年，三月成功拿到阿里offer，分享一波面经...

前言 不论是校招还是社招都避免不了各种⾯试、笔试，如何去准备这些东⻄就显得格外重要。不论是笔试还是⾯试都是有章可循的，我这个“有章可循”说的意思只是说应对技术⾯试是可以提前准备，所谓不打无准备的仗就是这个道理。 以下为大家&…...

编程日记 2023/4/14 6:57:37

餐饮店的运营需要考虑哪些方面

餐饮店的运营需要多方面的考虑和规划，以下是传递宝APP上一些常用的餐饮店运营方法： 1.定位：明确餐饮店的定位和目标客户群体，针对不同的客户需求，提供个性化的服务和产品，比如是附近的上班族，还…...

编程日记 2023/4/14 6:52:36

Multi-modal Alignment using Representation Codebook

Multi-modal Alignment using Representation Codebook 题目Multi-modal Alignment using Representation Codebook译题使用表示代码集的多模态对齐期刊/会议CVPR 摘要：对齐来自不同模态的信号是视觉语言表征学习（representation learning）的…...

编程日记 2023/4/14 6:47:35

关于vector的emplace_back和push_back的区别

实验代码&#xff1a; class A { public:A(int x) {x x;cout << "construct A" << endl;}A(const A& a) {x a.x;cout << "copy construct A" << endl;}A(const A&& a) {cout << "Move construct A"…...

编程日记 2023/5/31 12:23:14

Vue——表单输入绑定

目录 基本用法​ 文本 多行文本 复选框​ 选择器​ 值绑定​ 复选框 单选按钮 选择器选项 修饰符​ .lazy​ .number​ .trim​ 组件上的 v-model​ 在前端处理表单时&#xff0c;我们常常需要将表单输入框的内容同步给 JavaScript 中相应的变量。手动连接值绑定…...

编程日记 2023/4/14 6:37:33

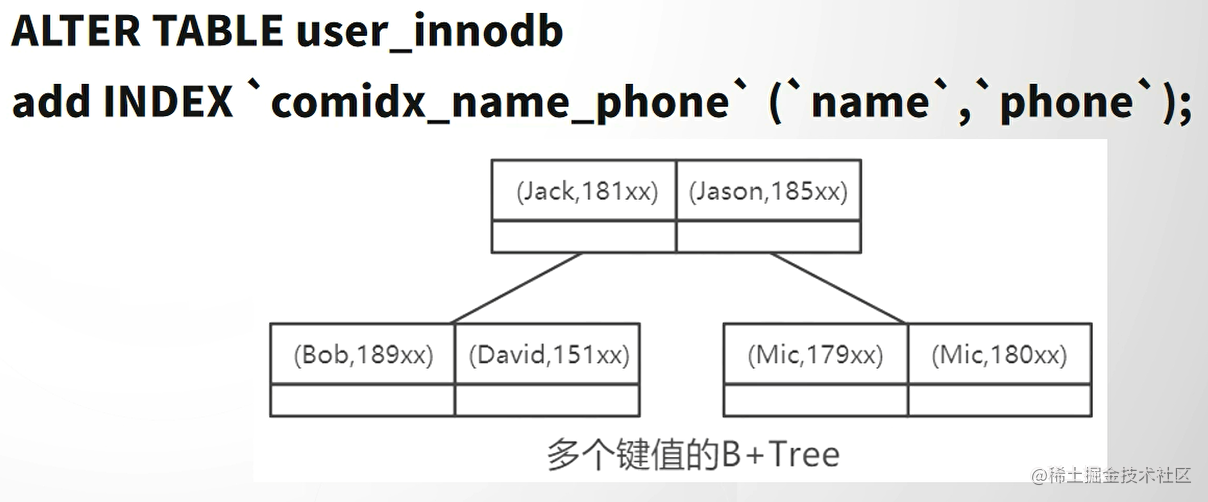
MySQL性能优化（二）索引

文章目录优化手段准备案例索引的本质索引的数据结构不同存储引擎中索引的实践MyIsam &#xff08;索引没有主次之分、都存放在MYI文件&#xff09;主键索引其他索引InnoDB&#xff08;数据即索引、索引即数据&#xff09;主键索引——聚集索引聚集索引其他索引没有主键的情况&a…...

编程日记 2023/5/31 12:23:31

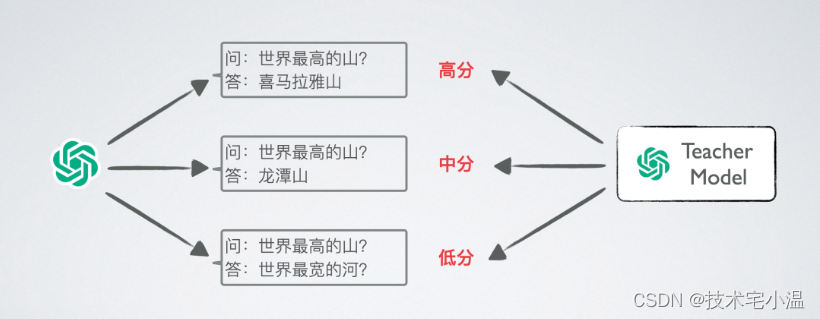
＜ 每日闲谈：你真的了解 “ ChatGPT ” 嘛 ？ ＞

< 每日闲谈&#xff1a;你真的了解 “ ChatGPT ” 嘛 &#xff1f; >&#x1f449; 前言&#x1f449; OpenAI的创立&#x1f449; ChatGPT有何过人之处&#xff1f;> 效果演示&#x1f449; OpenAI看家之作 — GPT自然语言模型> GPT发展史> 里程碑-GPT3> 从…...

编程日记 2023/5/31 14:35:55

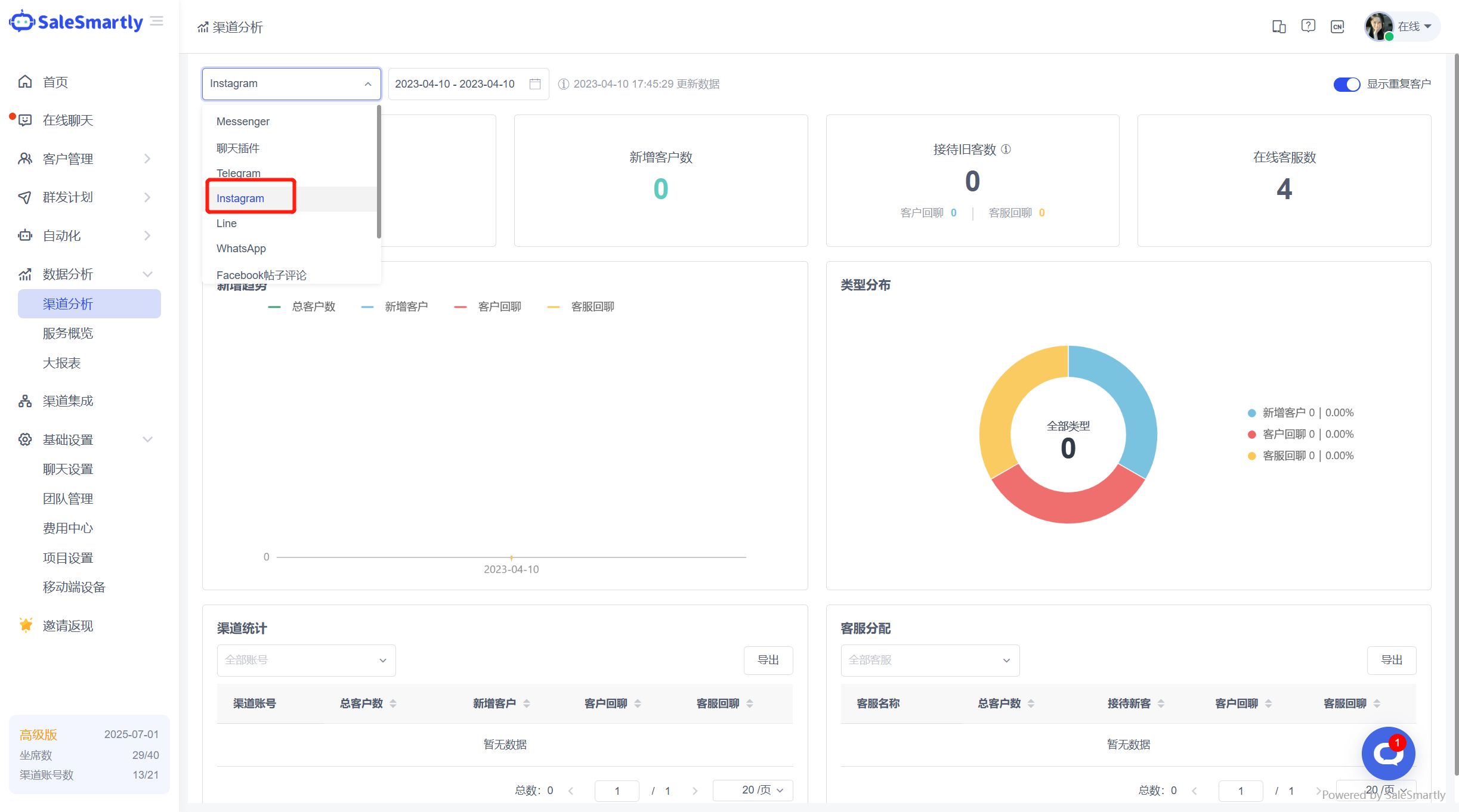
改善Instagram客户服务的6个技巧

Instagram仍然是全球前四大社交网络&#xff0c;按用户数量排名。它通过其创新的过滤器、内容创建工具、视频和卷轴选项继续增长并推动流量。这是一个平台&#xff0c;世界顶级名人和有影响力的人可以为全球用户提供有趣和令人印象深刻的内容。 但不仅仅是一个娱乐平台&#xf…...

编程日记 2023/4/14 6:22:29

8年经验之谈：4步解决测试与开发人员有争议的bug问题...

“开发认为不是bug&#xff0c;测试如何处理&#xff1f;”很多面试中&#xff0c;测试工程师都会被问到这个问题&#xff0c;不仅仅是面试&#xff0c;工作中测试人员也会遇到这类问题&#xff0c;甚至可能由于某种原因&#xff0c;无论是开发人员还是开发经理就是不愿修改程序…...

编程日记 2023/5/29 22:38:39

Linux日常小技巧shell脚本

在工作中我们常用shell脚本处理一些问题，这里整理了一些工作中常用的简单shell脚本。 定时备份文件 #!/bin/bash backup_dir="/data1/backup" src_dir="/data1/app" date_time=$(date +%Y%m%d_%H%M%S) tar -czvf ${backup_dir}/${date_time}.tar.gz ${sr…...

编程日记 2023/5/29 22:39:32

技术创业者必读：从验证想法到技术产品商业化的全方位解析

导语 | 技术创业之路往往充满着挑战和不确定性&#xff0c;对于初入创业领域的人来说&#xff0c;如何验证自己的创业想法是否有空间、如何选择靠谱的投资人、如何将技术产品商业化等问题都需要认真思考和解决。在「TVP 技术夜未眠」第六期直播中&#xff0c;正马软件 CTO、腾讯…...

编程日记 2023/4/14 6:07:25

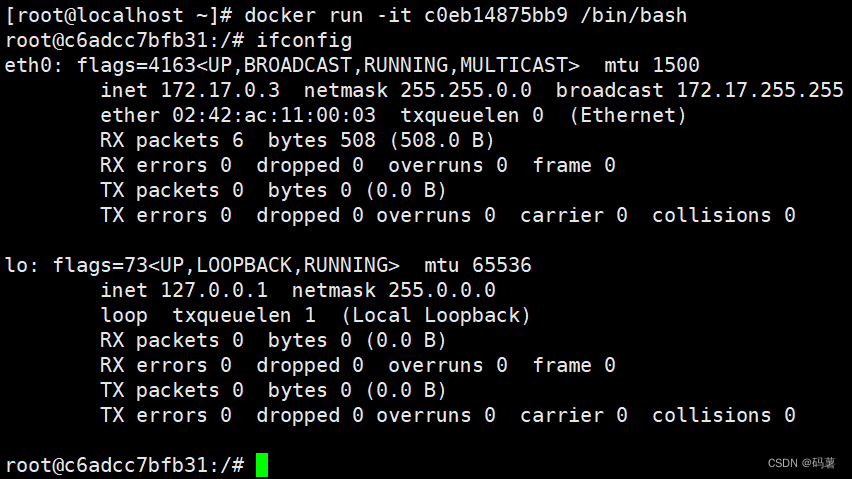
Docker Registry 本地镜像发布到私有库

本地镜像发布到私有库流程 是什么1 官方Docker Hub地址&#xff1a;https://hub.docker.com/&#xff0c;中国大陆访问太慢了且准备被阿里云取代的趋势&#xff0c;不太主流。2 Dockerhub、阿里云这样的公共镜像仓库可能不太方便&#xff0c;涉及机密的公司不可能提供镜像给公…...

编程日记 2023/5/30 7:23:21

Pytorch构建ResNet-50V2

&#x1f368; 本文为&#x1f517;365天深度学习训练营 中的学习记录博客 &#x1f366; 参考文章地址&#xff1a; 365天深度学习训练营-第J2周&#xff1a;ResNet-50V2算法实战与解析 &#x1f356; 作者&#xff1a;K同学啊 一、ResNetV2与ResNet结构对比 改进点 (a)origi…...

编程日记 2023/5/31 12:25:16

【01】PointNet论文解析

PointNet的应用 1.点云图像的分类&#xff08;整片点云是什么物体&#xff09; 2.点云图像的部件分割&#xff08;整片点云所代表的物体能拆分的结构&#xff09; 3.点云图像的语义分割&#xff08;将三维点云环境中不同的物体用不同的颜色区分开&#xff09; 补充 PointN…...

编程日记 2023/5/29 22:41:27

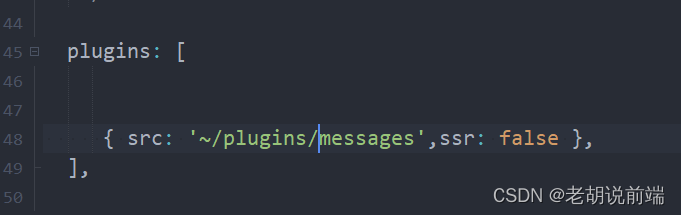
nuxt.js 在IE浏览器||其他浏览不识别document/window 情况处理

1 第一步注册到nuxt.config.js文件 2 第二步建立js 文件 import Vue from vue (function(){ if(process.client){ console.log(process.client) }else{ console.log(process.client) } if (!!window.ActiveXObject || "ActiveXObject" i…...

编程日记 2023/4/14 5:47:21

JavaEE简单示例——基于注解的SSM整合

基于注解的SSM整合 在之前我们进行了基于XML配置文件的整合&#xff0c;这次我们介绍基于注解的SSM框架的整合。基于注解的含义是将我们之前所有的配置文件用java类来代替&#xff0c;也就是我们会在Java类中编写之前我们之前在配置文件中编写的内容。 首先我们将之前我们编写…...

编程日记 2023/4/14 5:42:20

EFBG-06-250双比例阀放大器

EFBG-06-250双比例阀放大器特点&#xff1a; 1.本阀系仅供应驱动元件所需最低的压力及流量的入口节流式节能阀。 2.本阀可使油泵及马达侧的压力随时维持大于负载压0.6-0.9MPa的压差&#xff0c;因而可节省能耗。 3.外置比例放大器参数可调&#xff0c;维修更换简单。...

编程日记 2023/4/14 5:37:19

初级算法-栈与队列

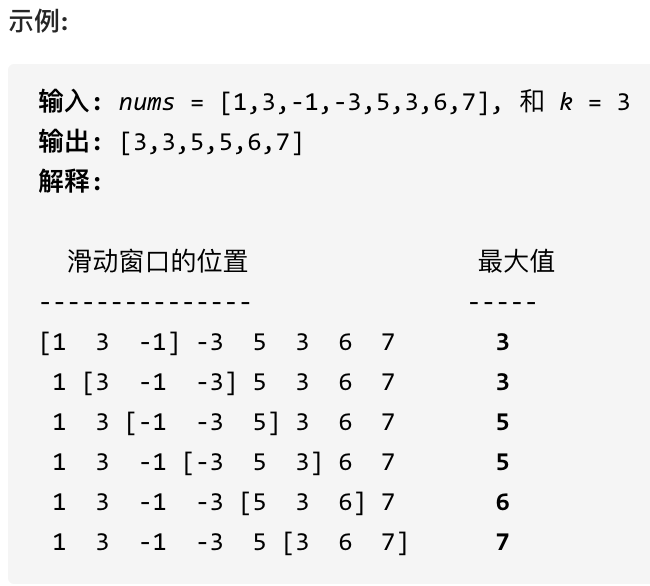
主要记录算法和数据结构学习笔记&#xff0c;新的一年更上一层楼&#xff01; 初级算法-栈与队列一、栈实现队列二、队列实现栈三、有效的括号四、删除字符串中的所有相邻重复项五、逆波兰表达式求值六、滑动窗口最大值七、前K个高频元素栈先进后出&#xff0c;不提供走访功能…...

编程日记 2023/5/31 21:40:33

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)

说明&#xff1a; 想象一下&#xff0c;你正在用eNSP搭建一个虚拟的网络世界&#xff0c;里面有虚拟的路由器、交换机、电脑&#xff08;PC&#xff09;等等。这些设备都在你的电脑里面“运行”&#xff0c;它们之间可以互相通信&#xff0c;就像一个封闭的小王国。 但是&#…...

编程新知 2026/2/8 4:37:17

【WiFi帧结构】

文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成&#xff1a;MAC头部frame bodyFCS&#xff0c;其中MAC是固定格式的&#xff0c;frame body是可变长度。 MAC头部有frame control&#xff0c;duration&#xff0c;address1&#xff0c;address2&#xff0c;addre…...

编程新知 2026/2/7 17:33:19

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

智能在线客服平台：数字化时代企业连接用户的 AI 中枢

随着互联网技术的飞速发展&#xff0c;消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁&#xff0c;不仅优化了客户体验&#xff0c;还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用&#xff0c;并…...

编程新知 2026/2/4 17:51:19

跨链模式：多链互操作架构与性能扩展方案

跨链模式&#xff1a;多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈&#xff1a;模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展&#xff08;H2Cross架构&#xff09;&#xff1a; 适配层&#xf…...

编程新知 2026/2/5 14:15:13

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

C++中string流知识详解和示例

一、概览与类体系 C 提供三种基于内存字符串的流&#xff0c;定义在 <sstream> 中&#xff1a; std::istringstream&#xff1a;输入流&#xff0c;从已有字符串中读取并解析。std::ostringstream&#xff1a;输出流&#xff0c;向内部缓冲区写入内容&#xff0c;最终取…...

编程新知 2025/11/30 11:30:47

并发编程 - go版

1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程&#xff0c;系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

编程新知 2026/1/31 6:50:52

基于Springboot+Vue的办公管理系统

角色&#xff1a; 管理员、员工 技术&#xff1a; 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能&#xff1a; 该办公管理系统是一个综合性的企业内部管理平台&#xff0c;旨在提升企业运营效率和员工管理水…...

编程新知 2026/1/31 8:55:37

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2026/1/28 4:50:33