C++之AVL树
文章目录
- 前言
- 一、概念
- 二、AVL树结点的定义
- 三、AVL树的插入
- 四、AVL树的旋转
- 1.右单旋的情况以及具体操作
- 抽象图
- h = 0
- h = 1
- h = 2
- 代码实现
- 2.左单旋的情况以及具体操作
- 抽象图
- 代码实现
- 3.右左双旋的情况以及具体操作
- 抽象图
- h = 0
- h = 1
- h = 2
- 3.左右双旋的情况以及具体操作
- 抽象图
- 5.总结
- 6.完整实现代码
- 7.验证
- 概念
- 主程序代码
- 8.性能
- 总结
前言
前面我们介绍了STL中的关联式容器map/set/multimap/mutiset等,我们可以发现它们的底层都是按照二叉搜索树来实现的,但是二叉搜索树自身有一些缺陷,当往二叉搜索树中插入的元素有序或者接近有序二叉搜索树就会退化为单支,其检索的时间复杂度就会退化为O(n)。因此map、set等关联式容器的底层结构是对搜索二叉树进行平衡处理的平衡二叉搜索树。
本节我们就来了解平衡搜索二叉树AVL树的相关概念。
一、概念
普通的搜索二叉树一旦数据有序或者接近有序就会造成二叉搜索树退化为单支,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:
**当向二叉搜索树中插入新结点后,如果能保证每个节点的左右子树高度之差不超过1(需要对树中结点进行调整)**即可降低树的高度,从而减少平均搜索长度。
一棵AVL树要具有以下性质:
- 该树如果是空树,那么它是AVL树;
- 它的左右子树是AVL树;
- 左右子树的高度差(命名为平衡因子)的绝对值不超过1(可以是1/0/-1)
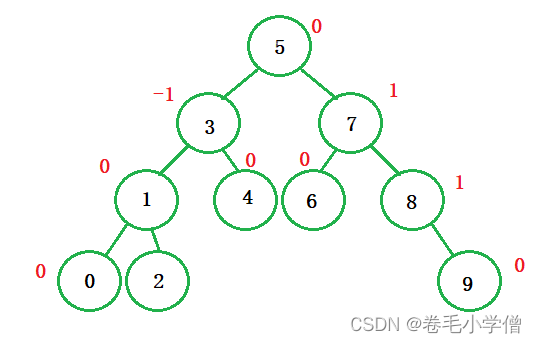
上图的红色标识的是该结点的平衡因子(这里的平衡因子使用右子树的高度减左子树的高度计算的)。
如果一棵二叉搜索树是高度平衡的,那么他就是AVL树。
假设该树有n个结点,其高度应保持在O(log2n)O(log_2 n)O(log2n),搜索时间复杂度为O(log2nlog_2 nlog2n)。
二、AVL树结点的定义
template<class K,class V>struct AVLnode//三叉链{pair<K, V> _kv;AVLnode(const pair<K,V>& kv):_kv(kv), _bf(0), _pleft(nullptr), _pright(nullptr), _pparent(nullptr){}AVLnode<K, V>* _pleft;//左孩子AVLnode<K, V>* _pright;//右孩子AVLnode<K, V>* _pparent;//双亲结点int _bf;//平衡因子};
三、AVL树的插入
实际上,AVL树就是在二叉搜索树的基础上增加了平衡因子,因此AVL树的插入可以分为两步:
- 按照二叉搜索树的插入方式插入新结点
- 调整结点的平衡因子
bool insert(const pair<K,V>& kv){//1.按照二叉搜索树的规则将节点插入到AVL树中node* newnode = new node(kv);node* cur = _root;if (_root == nullptr)//如果该树为空树,直接插入新节点,此时新节点是该树的根节点{_root = newnode;return true;}node* prev = nullptr;while (cur){prev = cur;if (cur->_kv.first > data){cur = cur->_pleft;}else if (cur->_kv.first < data){cur = cur->_pright;}else return false;//树中已经存在该元素,插入失败}if (prev->_kv.first > data){prev->_pleft = newnode;newnode->_pparent = prev;}else{prev->_pright = newnode;newnode->_pparent = prev;}node* pParent = prev;cur =newnode;//2.对结点的平衡因子进行更新,并检测新插入的结点是否破坏了AVL树的平衡性//调节平衡因子,在插入新结点前pparent的平衡因子有以下三种情况:-1, 0, 1//如果cur插在pparent的左边,给pparent的结点的平衡因子-1;//如果cur插在pparent的右边,给pparent的结点的平衡因子+1;//此时,pparent的平衡因子有以下三种情况,0,±1,±2//pparent平衡因子为0,说明新插入结点不影响该子树的高度,满足AVL树的性质,不再进行调整//pparent平衡因子为±1,说明插入前pparent的平衡因子为0,此时以pparent为根的子树的高度加1,需要继续向上更新平衡因子//pparent平衡因子为±2,说明插入前pparent的平衡因子为±1,此时pparent的平衡因子违反了AVL树的性质需要进行旋转操作while (pParent)//当pParent为空时,pParent就是根节点的父节点,就不需要再进行调整了{//更新父节点的平衡因子if (cur == pParent->_pleft){pParent->_bf--;}else if (cur == pParent->_pright){pParent->_bf++;}//检测更新后的平衡因子if (0 == pParent->_bf)//该子树的高度没变化,不用调整{break;}else if (1 == pParent->_bf || -1 == pParent->_bf)//该子树的高度增加了1,因此要继续向上调整平衡因子{cur = pParent;pParent = pParent->_pparent;}//3.破坏了AVL树的平衡性,我们就要对以pparent为根的子树就地旋转处理//旋转的目的://1)让这棵子树的左右高度差不超过1//2)旋转过程中保持它是搜索树//3)更新旋转后的平衡因子//4)让这棵树的高度与插入前保持一致(不会继续影响上层,不用继续向上调整)else if (2 == pParent->_bf || -2 == pParent->_bf){//右单旋//我的平衡因子为-1;父节点的平衡因子为-2.if (-2 == pParent->_bf && -1 == cur->_bf){RotateR(pParent);//更新平衡因子cur->_bf = 0;pParent->_bf = 0;}//左单旋else if (2 == pParent->_bf && 1 == cur->_bf){RotateL(pParent);//更新平衡因子cur->_bf = 0;pParent->_bf = 0;}//左右双旋else if (-2 == pParent->_bf && 1 == cur->_bf){node* SubR = cur->_pright;RotateL(cur);RotateR(pParent);//更新平衡因子//新增结点就是SubRif (SubR ->_bf == 0){cur->_bf = 0;pParent->_bf = 0;}//新增结点在SubR结点的左子树else if (SubR->_bf == -1){SubR->_bf = cur->_bf = 0;pParent->_bf = 1;}//新增结点在SubR结点的右子树else if (SubR->_bf == 1){SubR->_bf = pParent->_bf = 0;cur->_bf = -1;}else{assert(false);}}//右左双旋else if (2 == pParent->_bf && -1 == cur->_bf){node* SubL = cur->_pleft;RotateR(cur);RotateL(pParent);//更新平衡因子//新增结点就是SubLif (SubL->_bf == 0){cur->_bf = 0;pParent->_bf = 0;}//新增结点在SubL结点的左子树else if (SubL ->_bf == -1){SubL->_bf = pParent->_bf = 0;cur->_bf = 1;}//新增结点在SubL结点的右子树else if (SubL->_bf == 1){SubL->_bf = cur->_bf = 0;pParent->_bf = -1;}else{assert(false);}}return true;}else//如果以上的程序哪里出现问题就会直接报错{assert(false);}}return true;}private:AVLnode<T>* _root;};
四、AVL树的旋转
1.右单旋的情况以及具体操作
抽象图
先看如下的抽象图:

图中a,b,c是高度为h的子树,红色数字是插入前该节点的平衡因子。
新增结点导致要向上更新平衡因子,如果父节点的平衡因子为-2,且当前结点的平衡因子为-1时,我们就要进行右单旋。
那么如何进行右单旋呢?旋转处理之后平衡因子又是如何更新的呢?
要由具体的解决方法推出抽象的解决方法,因此下面我们具体分析当h分别为0/1/2时,我们的解决方法:
h = 0
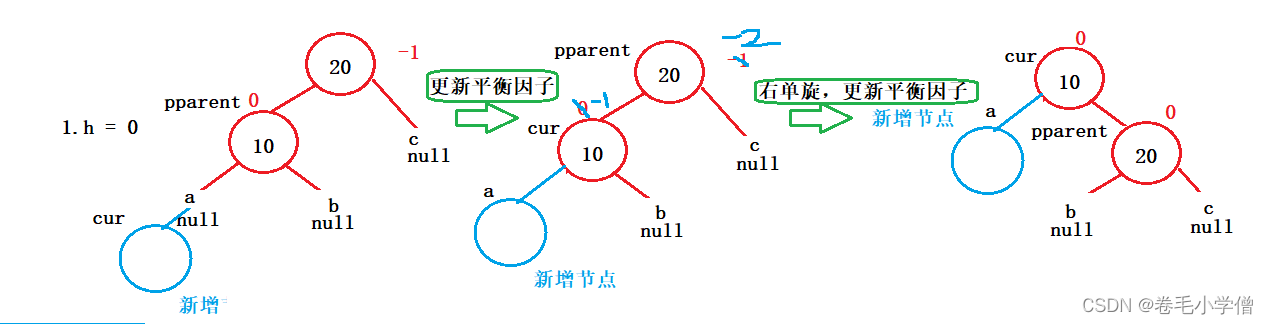
如图,当h = 0时,在a处新增节点,按照图中步骤使用右单旋对该子树进行调整,最后更新平衡因子即可。
h = 1
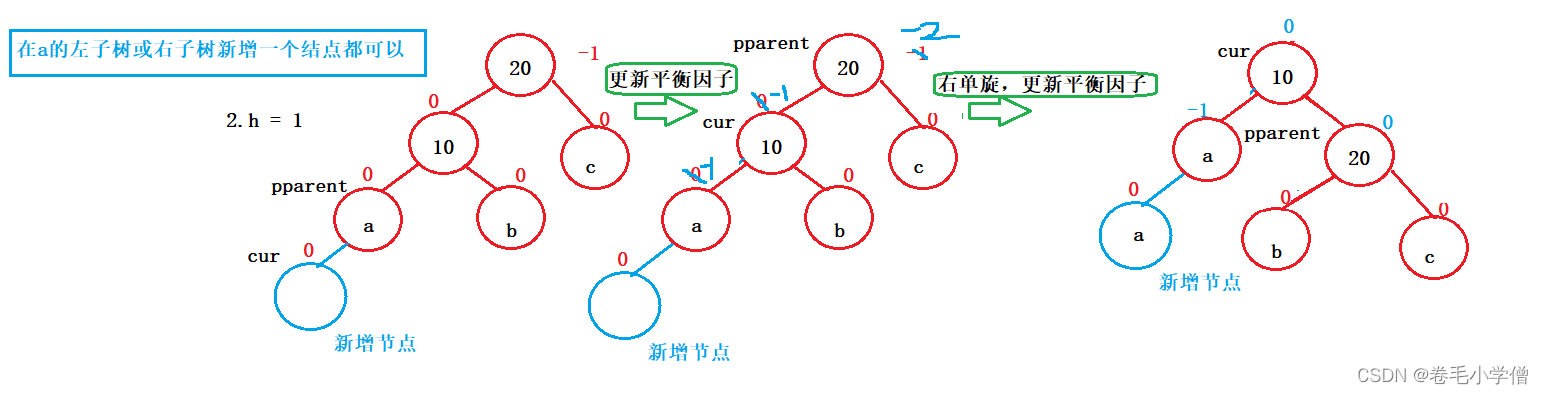
如图,当h = 1时,在a结点的左右子结点任意一个位置新增节点,按照图中步骤使用右单旋对该子树进行调整,最后更新平衡因子即可。
h = 2
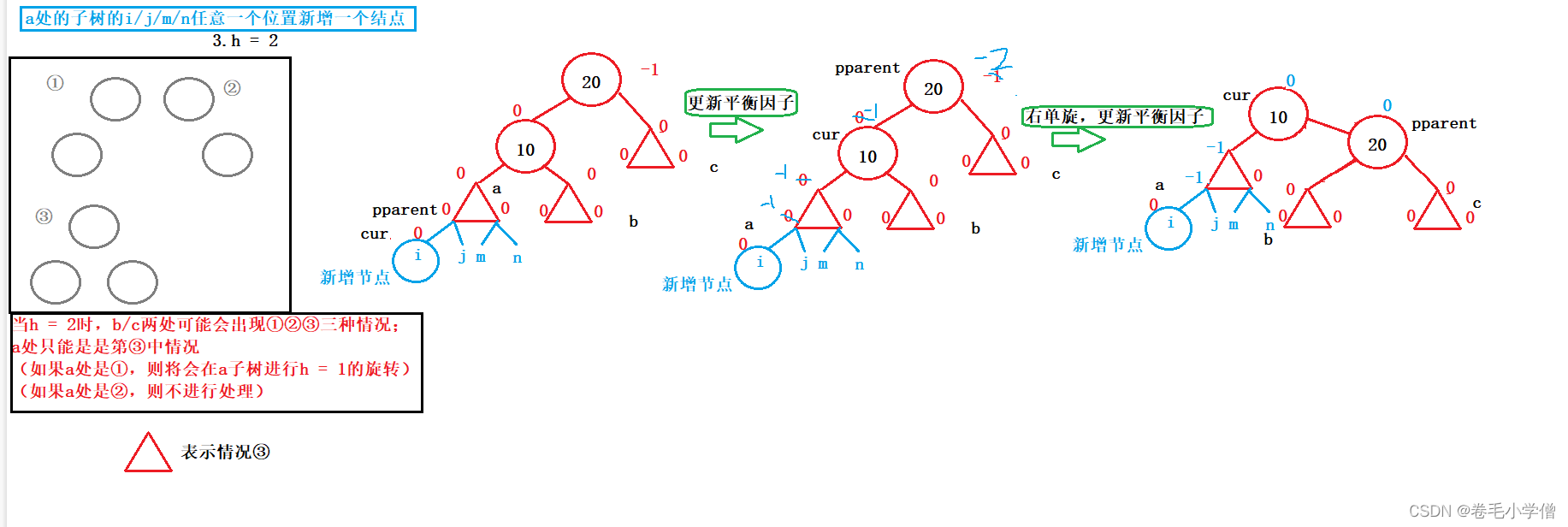
如图,当h = 2时,在a子树的i/j/m/n等四个位置的任意一个位置新增节点,按照图中步骤使用右单旋对该子树进行调整,最后更新平衡因子即可。
总结:根据以上三种情况我们可以得出,新增节点向上调整平衡因子的过程中,如果出现父节点的平衡因子为-2,当前结点的平衡因子为-1的情况,就以父节点为轴进行右单旋,之后更新父节点和当前结点的平衡因子为0即可。
代码实现
//左单旋(父节点平衡因子为2,右孩子平衡因子为1)void RotateL(node* parent){node* SubR = parent->_pright;node* SubRL = SubR->_pleft;node* Grandpa = parent->_pparent;//祖父parent->_pright = SubRL;if (SubRL){SubRL->_pparent = parent;}SubR->_pleft = parent;parent->_pparent = SubR;SubR->_pparent = Grandpa;//更新祖父的孩子结点if (Grandpa == nullptr)//pParent此时是根节点{_root = SubR;//更新cur为根节点_root ->_pparent = nullptr;}else{if (parent == Grandpa->_pleft){Grandpa->_pleft = SubR;}else{Grandpa->_pright = SubR;}}}
2.左单旋的情况以及具体操作
抽象图

图中a,b,c是高度为h的子树,红色数字是插入前该节点的平衡因子。
新增结点导致要向上更新平衡因子,如果父节点的平衡因子为2,且当前结点的平衡因子为1时,我们就要进行左单旋。
左单旋与右单旋的方法类似,没有特殊情况,因此这里只介绍当h = 0时的情况:
当h = 0时,在c位置新增结点
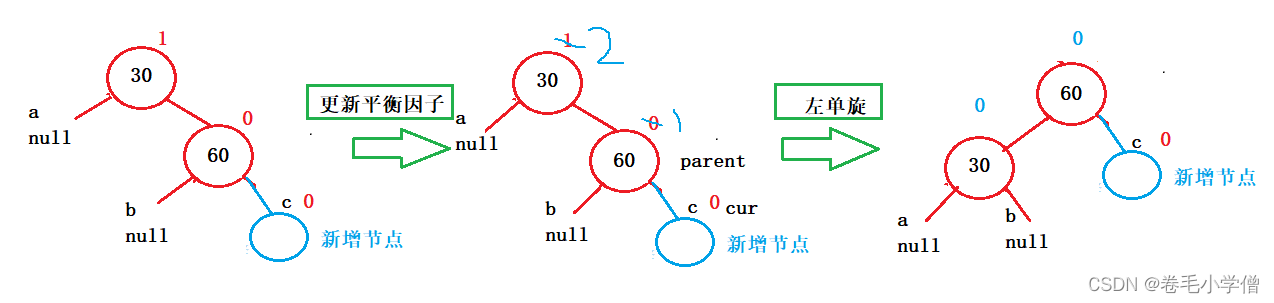
可以看出,当父节点为2且当前结点为1时,需要以父节点为轴进行左单旋,最后更新平衡因子。
代码实现
//右单旋(父节点平衡因子为-2,左孩子平衡因子为-1)void RotateR(node* parent){node* SubL = parent->_pleft;node* SubLR = SubL->_pright;node* Grandpa = parent->_pparent;//祖父parent->_pparent = SubL;SubL->_pright = parent;parent->_pleft = SubLR;if (SubLR)SubLR->_pparent = parent;SubL->_pparent = Grandpa;//更新祖父的孩子结点if (Grandpa == nullptr)//pParent此时是根节点{_root = SubL;SubL->_pparent = nullptr;}else{if (parent == Grandpa->_pleft){Grandpa->_pleft = SubL;}else{Grandpa->_pright = SubL;}}}
3.右左双旋的情况以及具体操作
我们设定:结点值为30的结点是parent,结点值为90的结点是pR,结点值为60的结点是pRL(起名字后方便操作)
抽象图
右左双旋的抽象图,其中a/d是高度为h的子树,b/c是高度为h-1的子树

先以pR结点为轴进行右单旋,再以parent结点为轴进行左单旋,最后更新平衡因子即可。
h = 0

h = 1
如果在b处新增结点(在60的左子树新增结点)

旋转后平衡因子的更新如下:
30结点的平衡因子为0;
60结点的平衡因子为0;
90结点的平衡因子为-1.
如果在c处新增结点(在60的右子树新增结点)
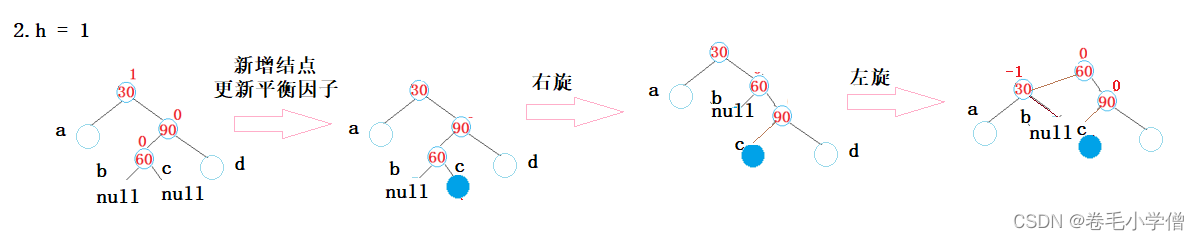
旋转后平衡因子的更新如下:
30结点的平衡因子为0;
60结点的平衡因子为0;
90结点的平衡因子为-1.
h = 2
在60的左右子树新增节点导致的旋转后的平衡因子的更新情况与h = 1时是一致的,因此只简单介绍在e处新增的情况。
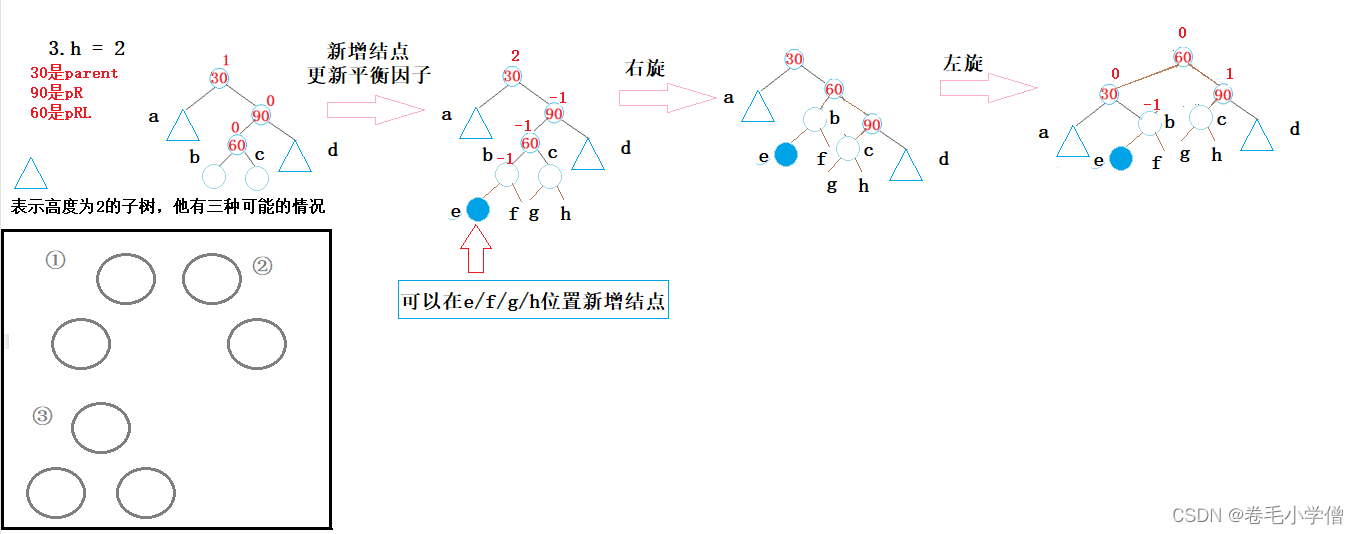
3.左右双旋的情况以及具体操作
我们设定:结点值为90的结点是parent,结点值为30的结点是pL,结点值为60的结点是pLR(起名字后方便操作)
抽象图

先以pL结点为轴进行左单旋,再以parent结点为轴进行右单旋,最后更新平衡因子即可。
如果新增的节点就是60,那么旋转后的平衡因子更新如下:
30结点/60结点/90结点的平衡因子都为0;
如果新增的节点在60结点的左子树,那么旋转后的平衡因子更新如下:
30结点的平衡因子为1;
60结点的平衡因子为0;
90结点的平衡因子为0。
如果新增的节点在60结点的右子树,那么旋转后的平衡因子更新如下:
30结点的平衡因子为0;
60结点的平衡因子为0;
90结点的平衡因子为-1。
左右双旋与右左双旋类似,可以参考理解,这里就不多赘述了。
5.总结
假如以parent为根的子树不平衡,即parent的平衡因子为2/-2,有以下几种情况:
- parent的平衡因子为2,说明parent的右子树高,设parent的右子树的根节点为pR
- 当pR的平衡因子为1时,执行左单旋;
- 当pR的平衡因子为-1时,执行右左双旋。
- parent的平衡因子为-2,说明parent的左子树高,设parent的左子树的根节点为pL
- 当pL的平衡因子为-1,执行右单旋;
- 当pL的平衡因子为1,执行左右双旋。
旋转结束后,原parent为根的子树高度已平衡,不需要再向上更新。
6.完整实现代码
namespace Jinger
{template<class K,class V>struct AVLnode//三叉链{pair<K, V> _kv;AVLnode(const pair<K,V>& kv):_kv(kv), _bf(0), _pleft(nullptr), _pright(nullptr), _pparent(nullptr){}AVLnode<K, V>* _pleft;//左孩子AVLnode<K, V>* _pright;//右孩子AVLnode<K, V>* _pparent;//双亲结点int _bf;//平衡因子};template<class K, class V>struct AVLTree{typedef AVLnode<K, V> node;AVLTree():_root(nullptr){}//左单旋(父节点平衡因子为2,右孩子平衡因子为1)void RotateL(node* parent){node* SubR = parent->_pright;node* SubRL = SubR->_pleft;node* Grandpa = parent->_pparent;//祖父parent->_pright = SubRL;if (SubRL){SubRL->_pparent = parent;}SubR->_pleft = parent;parent->_pparent = SubR;SubR->_pparent = Grandpa;//更新祖父的孩子结点if (Grandpa == nullptr)//pParent此时是根节点{_root = SubR;//更新cur为根节点_root ->_pparent = nullptr;}else{if (parent == Grandpa->_pleft){Grandpa->_pleft = SubR;}else{Grandpa->_pright = SubR;}}}//右单旋(父节点平衡因子为-2,左孩子平衡因子为-1)void RotateR(node* parent){node* SubL = parent->_pleft;node* SubLR = SubL->_pright;node* Grandpa = parent->_pparent;//祖父parent->_pparent = SubL;SubL->_pright = parent;parent->_pleft = SubLR;if (SubLR)SubLR->_pparent = parent;SubL->_pparent = Grandpa;//更新祖父的孩子结点if (Grandpa == nullptr)//pParent此时是根节点{_root = SubL;SubL->_pparent = nullptr;}else{if (parent == Grandpa->_pleft){Grandpa->_pleft = SubL;}else{Grandpa->_pright = SubL;}}}bool insert(const pair<K,V>& kv){//1.按照二叉搜索树的规则将节点插入到AVL树中node* newnode = new node(kv);node* cur = _root;if (_root == nullptr)//如果该树为空树,直接插入新节点,此时新节点是该树的根节点{_root = newnode;return true;}node* prev = nullptr;while (cur){prev = cur;if (cur->_kv.first > kv.first){cur = cur->_pleft;}else if (cur->_kv.first < kv.first){cur = cur->_pright;}else return false;//树中已经存在该元素,插入失败}if (prev->_kv.first > kv.first){prev->_pleft = newnode;newnode->_pparent = prev;}else{prev->_pright = newnode;newnode->_pparent = prev;}node* pParent = prev;cur =newnode;//2.对结点的平衡因子进行更新,并检测新插入的结点是否破坏了AVL树的平衡性//调节平衡因子,在插入新结点前pparent的平衡因子有以下三种情况:-1, 0, 1//如果cur插在pparent的左边,给pparent的结点的平衡因子-1;//如果cur插在pparent的右边,给pparent的结点的平衡因子+1;//此时,pparent的平衡因子有以下三种情况,0,±1,±2//pparent平衡因子为0,说明新插入结点不影响该子树的高度,满足AVL树的性质,不再进行调整//pparent平衡因子为±1,说明插入前pparent的平衡因子为0,此时以pparent为根的子树的高度加1,需要继续向上更新平衡因子//pparent平衡因子为±2,说明插入前pparent的平衡因子为±1,此时pparent的平衡因子违反了AVL树的性质需要进行旋转操作while (pParent)//当pParent为空时,pParent就是根节点的父节点,就不需要再进行调整了{//更新父节点的平衡因子if (cur == pParent->_pleft){pParent->_bf--;}else if (cur == pParent->_pright){pParent->_bf++;}//检测更新后的平衡因子if (0 == pParent->_bf)//该子树的高度没变化,不用调整{break;}else if (1 == pParent->_bf || -1 == pParent->_bf)//该子树的高度增加了1,因此要继续向上调整平衡因子{cur = pParent;pParent = pParent->_pparent;}//3.破坏了AVL树的平衡性,我们就要对以pparent为根的子树就地旋转处理//旋转的目的://1)让这棵子树的左右高度差不超过1//2)旋转过程中保持它是搜索树//3)更新旋转后的平衡因子//4)让这棵树的高度与插入前保持一致(不会继续影响上层,不用继续向上调整)else if (2 == pParent->_bf || -2 == pParent->_bf){//右单旋//我的平衡因子为-1;父节点的平衡因子为-2.if (-2 == pParent->_bf && -1 == cur->_bf){RotateR(pParent);//更新平衡因子cur->_bf = 0;pParent->_bf = 0;}//左单旋else if (2 == pParent->_bf && 1 == cur->_bf){RotateL(pParent);//更新平衡因子cur->_bf = 0;pParent->_bf = 0;}//左右双旋else if (-2 == pParent->_bf && 1 == cur->_bf){node* SubR = cur->_pright;RotateL(cur);RotateR(pParent);//更新平衡因子//新增结点就是SubRif (SubR ->_bf == 0){cur->_bf = 0;pParent->_bf = 0;}//新增结点在SubR结点的左子树else if (SubR->_bf == -1){SubR->_bf = cur->_bf = 0;pParent->_bf = 1;}//新增结点在SubR结点的右子树else if (SubR->_bf == 1){SubR->_bf = pParent->_bf = 0;cur->_bf = -1;}else{assert(false);}}//右左双旋else if (2 == pParent->_bf && -1 == cur->_bf){node* SubL = cur->_pleft;RotateR(cur);RotateL(pParent);//更新平衡因子//新增结点就是SubLif (SubL->_bf == 0){cur->_bf = 0;pParent->_bf = 0;}//新增结点在SubL结点的左子树else if (SubL ->_bf == -1){SubL->_bf = pParent->_bf = 0;cur->_bf = 1;}//新增结点在SubL结点的右子树else if (SubL->_bf == 1){SubL->_bf = cur->_bf = 0;pParent->_bf = -1;}else{assert(false);}}return true;}else//如果以上的程序哪里出现问题就会直接报错{assert(false);}}return true;}//获取根节点node* Getroot(){return _root;}private:node* _root;};
}
7.验证
概念
AVL树是在搜索二叉树的基础上加入了平衡因子的限制,因此要验证AVL树可以分为以下两个步骤:
- 验证其是否为搜索二叉树
- 验证其是否为平衡树(平衡因子)
- 每个结点子树高度差的绝对值不超过1
- 判断结点中的平衡因子计算是否正确
- 验证用例:
一般情况(仅进行单旋)
{16, 3, 7, 11, 9, 26, 18, 14, 15}
特殊情况(进行双旋)
{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}
主程序代码
下面是测试用的主程序代码,大家可以用它来检验AVL树实现代码的正确性:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<assert.h>
#include"AVL.h"
int _Height(Jinger::AVLnode<int,int>* pRoot)//计算树的最大高度
{if (pRoot == nullptr) return 0;return 1 + max(_Height(pRoot->_pleft), _Height(pRoot->_pright));
}
bool _IsBalanceTree(Jinger::AVLnode<int,int>* pRoot)
{// 空树也是AVL树if (nullptr == pRoot) return true;// 计算pRoot节点的平衡因子:即pRoot左右子树的高度差int leftHeight = _Height(pRoot->_pleft);int rightHeight = _Height(pRoot->_pright);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != pRoot->_bf || (diff > 1 || diff < -1))return false;// pRoot的左和右如果都是AVL树,则该树一定是AVL树return _IsBalanceTree(pRoot->_pleft) && _IsBalanceTree(pRoot ->_pright);
}
int main()
{Jinger::AVLTree<int,int> tree;vector<int> v{ 16, 3, 7, 11, 9, 26, 18, 14, 15};//vector<int> v{ 4, 2, 6, 1, 3, 5, 15, 7, 16, 14};for (auto it : v){cout << it << " ";tree.insert(make_pair(it,it));}int a = 0;bool ret = _IsBalanceTree(tree.Getroot());if (ret == 0) cout << "该树不是AVL树" << endl;else cout << "该树是AVL树" << endl;return 0;
}
8.性能
AVL树是一棵绝对平衡的搜索二叉树,它要求每个结点的左右子树的高度差的绝对值不超过1,这样可以保证查询时的时间复杂度(log2(N)log_2(N)log2(N))。但是如果对AVL树做一些结构修改的操作,它的性能就会比较低下,例如,插入元素时要维护其绝对平衡的性质,旋转的次数会比较多。其中删除的效果最差,有可能让旋转一直持续到根节点。
因此,如果需要一种查询高效且有序的数据结构,并且数据结构的个数为静态的(不会发生改变),可以考虑使用AVL树,但是如果该结构需要经常被修改AVL树就不太适合了。
总结
以上就是今天要讲的内容,本文介绍了C++中的AVL树的相关概念。本文作者目前也是正在学习C++相关的知识,如果文章中的内容有错误或者不严谨的部分,欢迎大家在评论区指出,也欢迎大家在评论区提问、交流。
最后,如果本篇文章对你有所启发的话,希望可以多多支持作者,谢谢大家!
相关文章:

C++之AVL树
文章目录前言一、概念二、AVL树结点的定义三、AVL树的插入四、AVL树的旋转1.右单旋的情况以及具体操作抽象图h 0h 1h 2代码实现2.左单旋的情况以及具体操作抽象图代码实现3.右左双旋的情况以及具体操作抽象图h 0h 1h 23.左右双旋的情况以及具体操作抽象图5.总结6.完整实现…...
【ROS2指南-2】入门 turtlesim 和 rqt
目标:安装并使用 turtlesim 包和 rqt 工具为即将到来的教程做准备。 教程级别:初学者 时间: 15分钟 内容 背景 先决条件 任务 1 安装turtlesim 2 启动turtlesim 3 使用turtlesim 4 安装rqt 5 使用 rqt 6 重新映射 7 关闭turtlesim …...

Python 进阶指南(编程轻松进阶):四、起个好名字
原文:http://inventwithpython.com/beyond/chapter4.html 计算机科学中最困难的两个问题是命名事物、缓存失效引起错误."这个经典的笑话,出自利昂班布里克之手,并基于菲尔卡尔顿的一句话,包含了一个真理的核心:很…...

STL容器适配器之<priority_queue>
文章目录测试环境priority_queue介绍头文件模块类定义对象构造元素访问元素插入和删除容器大小迭代器其他函数测试环境 系统:ubuntu 22.04.2 LTS 64位 gcc版本:11.3.0 编辑器:vsCode 1.76.2 priority_queue介绍 容器适配器。支持在末端插入…...

线程——线程同步
案例:卖票 需求:某电影院目前正在上映国产大片,共有100张票,而它有三个窗口卖票,请设计一个程序模拟该电影院卖票 思路: 定义一个类SellTicket实现Runnable接口,里面定义一个成员变量ÿ…...

安卓录屏使用VirtualDisplay虚拟屏幕;MediaRecorder,媒体录影机;
1.跟截屏一样,判断权限,然后在onActivityResult里面给mediaProjection赋能; 2.初始化录像机: //初始化Recorder录像机 fun initRecorderStart() { //新建Recorder val displayMetrics DisplayMetrics() val width displayMetri…...
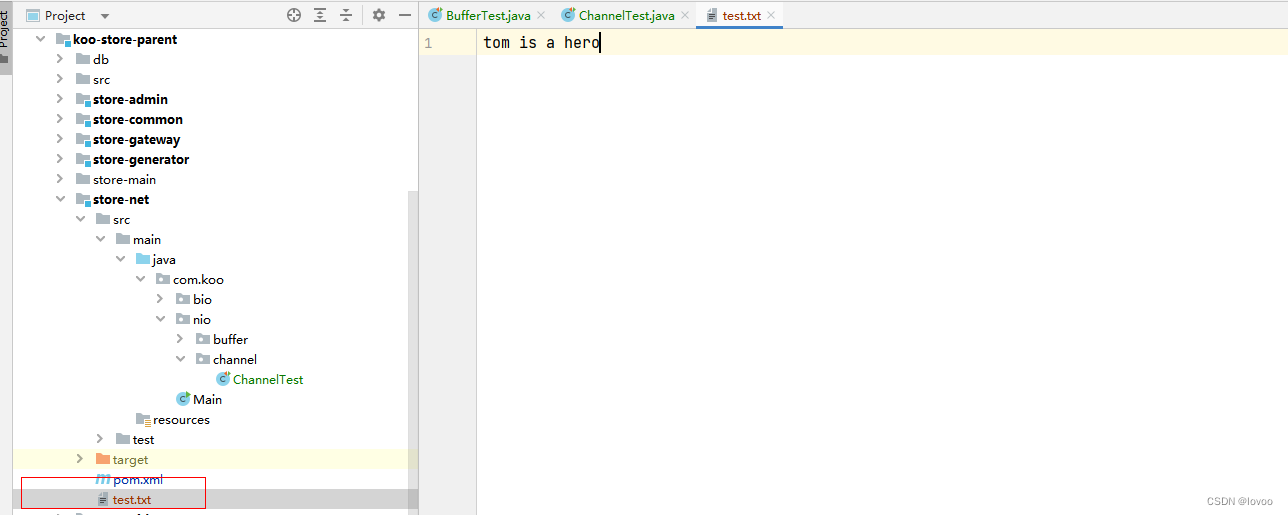
Java FileChannel文件的读写实例
一、概述: 文件通道FileChannel是用于读取,写入,文件的通道。FileChannel只能被InputStream、OutputStream、RandomAccessFile创建。使用fileChannel.transferTo()可以极大的提高文件的复制效率,他们读和写直接建立了通道&#x…...

2023 年男生还推荐报计算机专业吗?
计算机专业确实是一个非常热门的专业,就业前景也很广阔。 但是,近些年随着各个大学对计算机专业及其相关专业疯狂扩招,而且每年的毕业人口都在增多,行业是根本容纳不下的,就业竞争力度也急剧上升。因此,选…...
(javapython))
【华为OD机试真题】积木最远距离(相同数字的积木游戏1)(javapython)
相同数字的积木游戏1 知识点数组循环map 时间限制:1s 空间限制:256MB 限制语言:不限 题目描述: 小华和小薇一起通过玩积木游戏学习数学。 他们有很多积木,每个积木块上都有一个数字,积木块上的数字可能相同。 小华随机拿一些积木挨着排成一排,请小薇找到这排积木中数…...

STM32F103RCT6驱动SG90舵机-完成正反转角度控制
一、SG90舵机介绍 SG90是一种微型舵机,也被称为伺服电机。它是一种小型、低成本的直流电机,通常用于模型和机器人控制等应用中。SG90舵机可以通过电子信号来控制其精确的位置和速度。它具有体积小、重量轻、响应快等特点,因此在各种小型机械…...
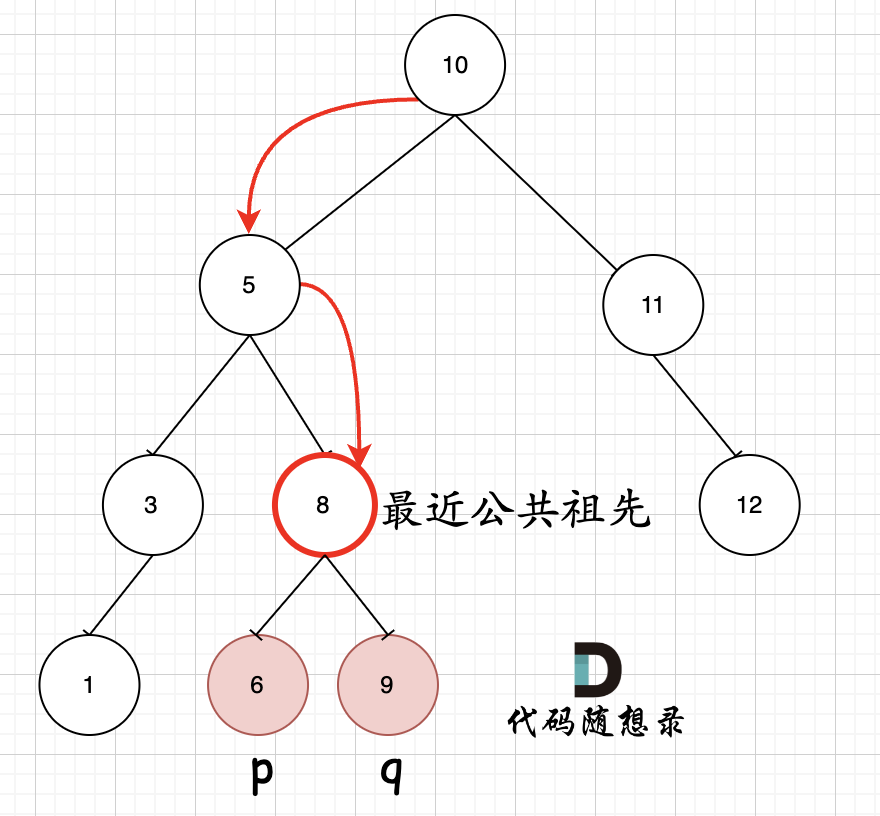
【4.13(补)】二叉搜索树的遍历、插入、删除
文章目录二叉搜索树的最近公共祖先二叉搜索树中的插入操作删除二叉搜索树中的节点二叉搜索树的最近公共祖先 235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode) 因为二叉搜索树是有序的,第一次找到p和q中间的值,就是最近的公共祖先…...

Web 攻防之业务安全:Callback自定义测试(触发XSS漏洞)
Web 攻防之业务安全:Callback自定义测试 业务安全是指保护业务系统免受安全威胁的措施或手段。广义的业务安全应包括业务运行的软硬件平台(操作系统、数据库,中间件等)、业务系统自身(软件或设备)、业务所提…...

Java访问底层操作系统
native方法定义: 简单地讲,一个Native Method就是一个java调用非java代码的接口。一个Native Method是这样一个java的方法:该方法的实现由非java语言实现,比如C。这个特征并非java所特有,很多其它的编程语言都有这一机…...
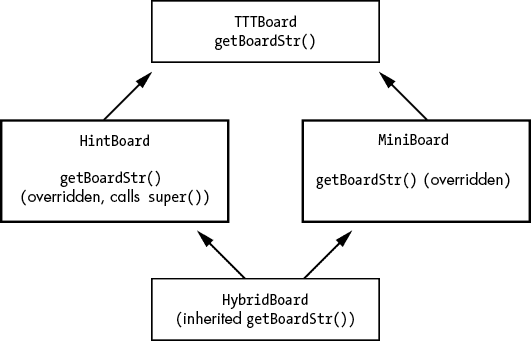
Python 进阶指南(编程轻松进阶):十六、面向对象编程和继承
原文:http://inventwithpython.com/beyond/chapter16.html 定义一个函数,并从几个地方调用它,可以省去复制和粘贴源代码的麻烦。不复制代码是一个很好的实践,因为如果你需要修改它(无论是为了修复一个错误还是添加新特…...

【计算机系统结构】第一章 计算机系统结构基本概念
文章目录第一章 计算机系统结构基本概念1.1 计算机系统结构的概念1.2 计算机体系结构的发展1.3 系统结构中并行性的发展1.4 系统结构的设计1.5 定量分析技术基础第一章 计算机系统结构基本概念 课程内容 A I P S N 工业革命 1.1 计算机系统结构的概念 引言 第一台通用计算机 …...

e2fsprogs logsave Ubuntu 安装失败 unable to make backup link of ‘./usr/bin/chattr‘
最近给服务器从 Ubuntu 18.04 LTS 升级到 20.04 LTS,过程中崩溃,重新尝试执行,提示依赖错误。这时候 apt install 所有的东西都会报错,提示依赖不满足。(这里的报错忘了复制了)执行 apt upgrade 也是一样。…...
)
在排序数组中查找元素的第一个和最后一个位置(二分查找进阶)
在写这个题目之前需要大家自行看一下我之前写的博客有关二分查找思想,如何判断什么时候使用二分查找以及边界值的确定:二分查找思想力扣实例_徐憨憨!的博客-CSDN博客 题目:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定…...
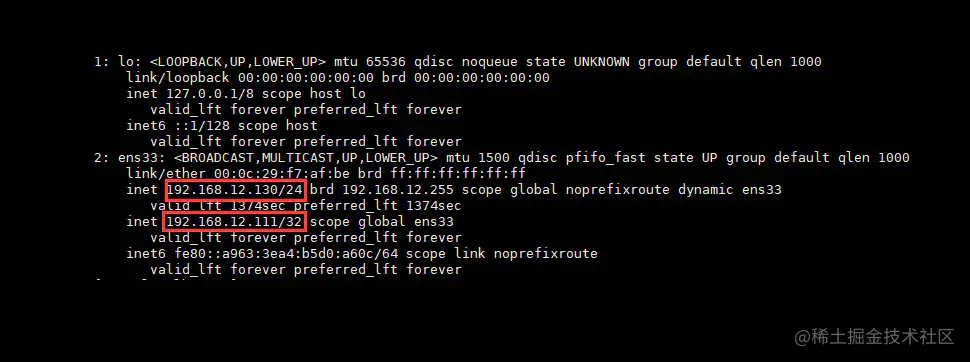
1 Nginx跨域配置
跨域问题在之前的单体架构开发中,其实是比较少见的问题,除非是需要接入第三方SDK时,才需要处理此问题。但随着现在前后端分离、分布式架构的流行,跨域问题也成为了每个Java开发必须要懂得解决的一个问题。 跨域问题产生的原因 产…...
ChatGTP如此强大,我们普通人如何利用它来赚钱?
我从效率提升的角度,分享了我这段时间看到的、用到的,以及思考的一些内容。 最近这段时间,我算是密集的学习。不得不说,优质的资料在推特和油管上特别多,看科技大佬的分享真是一种享受。 很多大神也会录制各种详细的…...
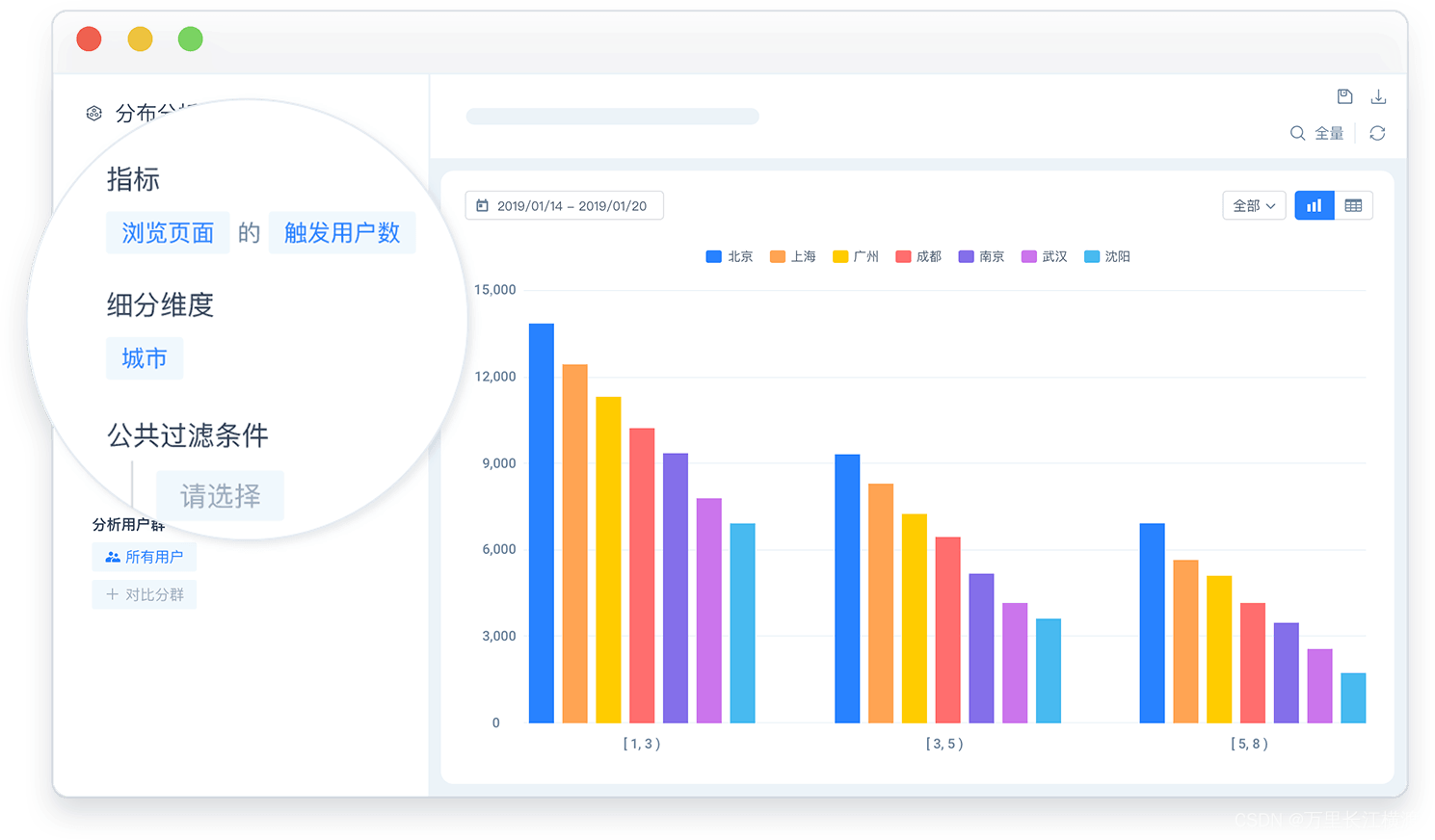
常见的九种大数据分析模型
常见的9种大数据分析模型分别为: 事件分析、 属性分析、 渠道分析、 Session分析、 留存分析、 归因分析、 漏斗分析、 路径分析、 分布分析 1、【事件分析】 事件分析,是指用户在 APP、网站等应用上发生的行为,即何人,何时&…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
