【4.13(补)】二叉搜索树的遍历、插入、删除
文章目录
- 二叉搜索树的最近公共祖先
- 二叉搜索树中的插入操作
- 删除二叉搜索树中的节点
二叉搜索树的最近公共祖先
-
235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
因为二叉搜索树是有序的,第一次找到p和q中间的值,就是最近的公共祖先。
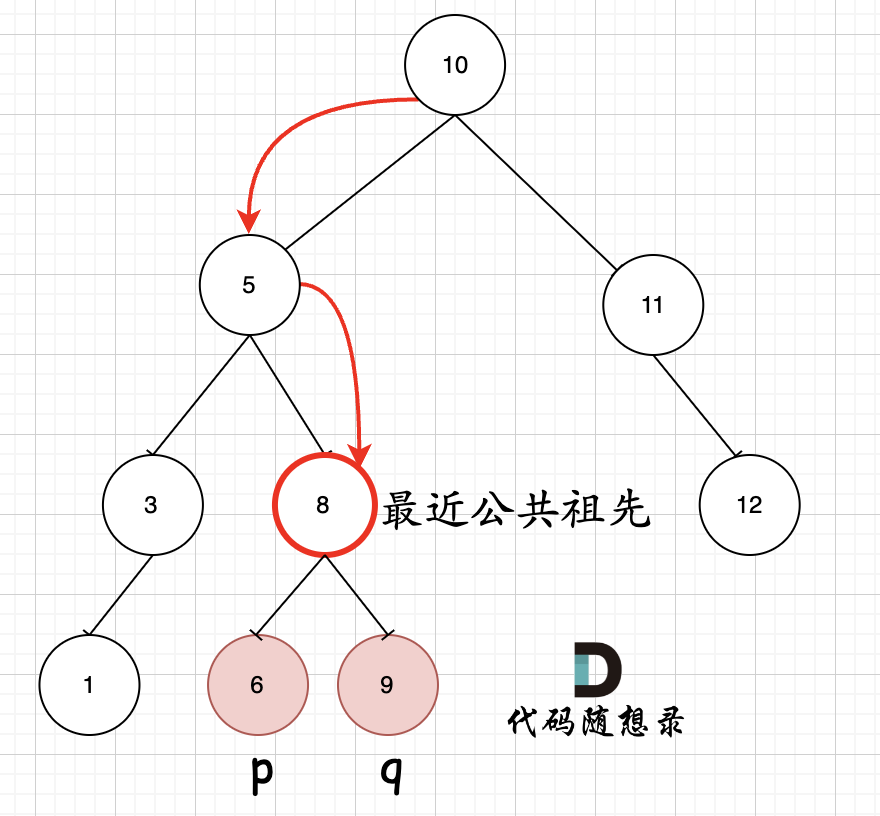
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(p.val > q.val){return traverse(root , q , p);}else{return traverse(root , p , q);}}TreeNode traverse(TreeNode root , TreeNode p , TreeNode q){if(root == null) return null;if(root.val >= p.val && root.val <= q.val){return root;}TreeNode left = traverse(root.left , p , q);TreeNode right = traverse(root.right , p , q);return left == null ? right : left;} }
二叉搜索树中的插入操作
-
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
本题只需要找到空的节点进行插入即可。
-
通过函数的返回值,进行插入操作。
class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {if(root == null){TreeNode node = new TreeNode(val);return node;}if(root.val > val) root.left = insertIntoBST(root.left , val);if(root.val < val) root.right = insertIntoBST(root.right , val);return root;} } -
通过保存父节点的值,进行插入操作。
class Solution {TreeNode parent;public TreeNode insertIntoBST(TreeNode root, int val) {if(root == null) return new TreeNode(val);traverse(root , val);return root;}void traverse(TreeNode root , int val){if(root == null){TreeNode node = new TreeNode(val);if(parent.val > val){parent.left = node;}else{parent.right = node;}return ;}parent = root;if(root.val > val) traverse(root.left , val);if(root.val < val) traverse(root.right , val);} }
-
删除二叉搜索树中的节点
-
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
二叉搜索树的删除涉及到五个方面,尤其要注意,当删除的节点左右都有子节点时,要将左子节点放到右子节点的最左边。这才符合二叉搜索树的原则。class Solution {public TreeNode deleteNode(TreeNode root, int key) {//说明删除的节点不在二叉树内,直接返回null。if(root == null) return root;//root为当前要删除的节点if(root.val == key){//2:如果左右孩子都为空,直接返回nullif(root.left == null && root.right == null){return null;}//3:删除节点的左孩子为空,右孩子不为空else if(root.left == null){//返回右孩子的根节点补位。return root.right;}//4:删除节点的左孩子不为空,右孩子为空。else if(root.right == null){return root.left;}//5:左右都不为空else if(root.left != null && root.right != null){//找到左孩子节点TreeNode left = root.left;//将左孩子节点放在删除节点的右子树最左面的左孩子上。TreeNode right_left = root.right;while(right_left.left != null){right_left = right_left.left; }right_left.left = left;return root.right;}}if(root.val > key) root.left = deleteNode(root.left , key);if(root.val < key) root.right = deleteNode(root.right , key);//说明不是我要找的节点,返回rootreturn root;} }
相关文章:

【4.13(补)】二叉搜索树的遍历、插入、删除
文章目录二叉搜索树的最近公共祖先二叉搜索树中的插入操作删除二叉搜索树中的节点二叉搜索树的最近公共祖先 235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode) 因为二叉搜索树是有序的,第一次找到p和q中间的值,就是最近的公共祖先…...

Web 攻防之业务安全:Callback自定义测试(触发XSS漏洞)
Web 攻防之业务安全:Callback自定义测试 业务安全是指保护业务系统免受安全威胁的措施或手段。广义的业务安全应包括业务运行的软硬件平台(操作系统、数据库,中间件等)、业务系统自身(软件或设备)、业务所提…...

Java访问底层操作系统
native方法定义: 简单地讲,一个Native Method就是一个java调用非java代码的接口。一个Native Method是这样一个java的方法:该方法的实现由非java语言实现,比如C。这个特征并非java所特有,很多其它的编程语言都有这一机…...
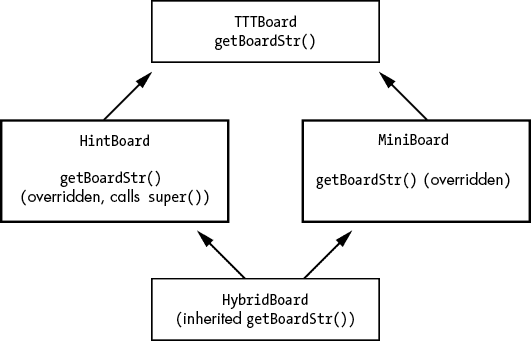
Python 进阶指南(编程轻松进阶):十六、面向对象编程和继承
原文:http://inventwithpython.com/beyond/chapter16.html 定义一个函数,并从几个地方调用它,可以省去复制和粘贴源代码的麻烦。不复制代码是一个很好的实践,因为如果你需要修改它(无论是为了修复一个错误还是添加新特…...

【计算机系统结构】第一章 计算机系统结构基本概念
文章目录第一章 计算机系统结构基本概念1.1 计算机系统结构的概念1.2 计算机体系结构的发展1.3 系统结构中并行性的发展1.4 系统结构的设计1.5 定量分析技术基础第一章 计算机系统结构基本概念 课程内容 A I P S N 工业革命 1.1 计算机系统结构的概念 引言 第一台通用计算机 …...

e2fsprogs logsave Ubuntu 安装失败 unable to make backup link of ‘./usr/bin/chattr‘
最近给服务器从 Ubuntu 18.04 LTS 升级到 20.04 LTS,过程中崩溃,重新尝试执行,提示依赖错误。这时候 apt install 所有的东西都会报错,提示依赖不满足。(这里的报错忘了复制了)执行 apt upgrade 也是一样。…...
)
在排序数组中查找元素的第一个和最后一个位置(二分查找进阶)
在写这个题目之前需要大家自行看一下我之前写的博客有关二分查找思想,如何判断什么时候使用二分查找以及边界值的确定:二分查找思想力扣实例_徐憨憨!的博客-CSDN博客 题目:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定…...
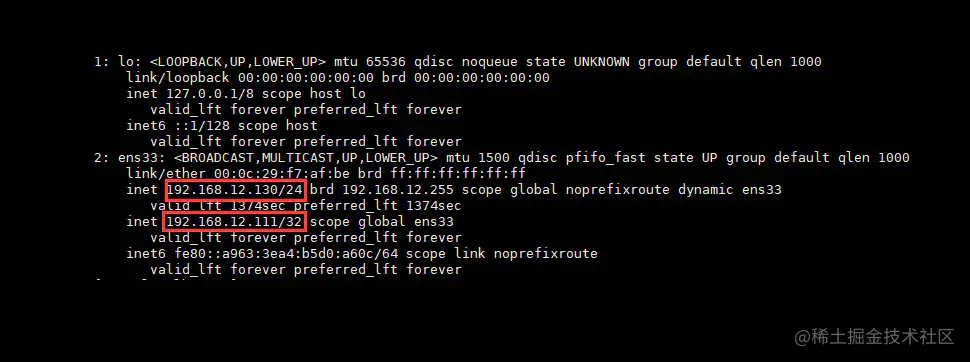
1 Nginx跨域配置
跨域问题在之前的单体架构开发中,其实是比较少见的问题,除非是需要接入第三方SDK时,才需要处理此问题。但随着现在前后端分离、分布式架构的流行,跨域问题也成为了每个Java开发必须要懂得解决的一个问题。 跨域问题产生的原因 产…...
ChatGTP如此强大,我们普通人如何利用它来赚钱?
我从效率提升的角度,分享了我这段时间看到的、用到的,以及思考的一些内容。 最近这段时间,我算是密集的学习。不得不说,优质的资料在推特和油管上特别多,看科技大佬的分享真是一种享受。 很多大神也会录制各种详细的…...
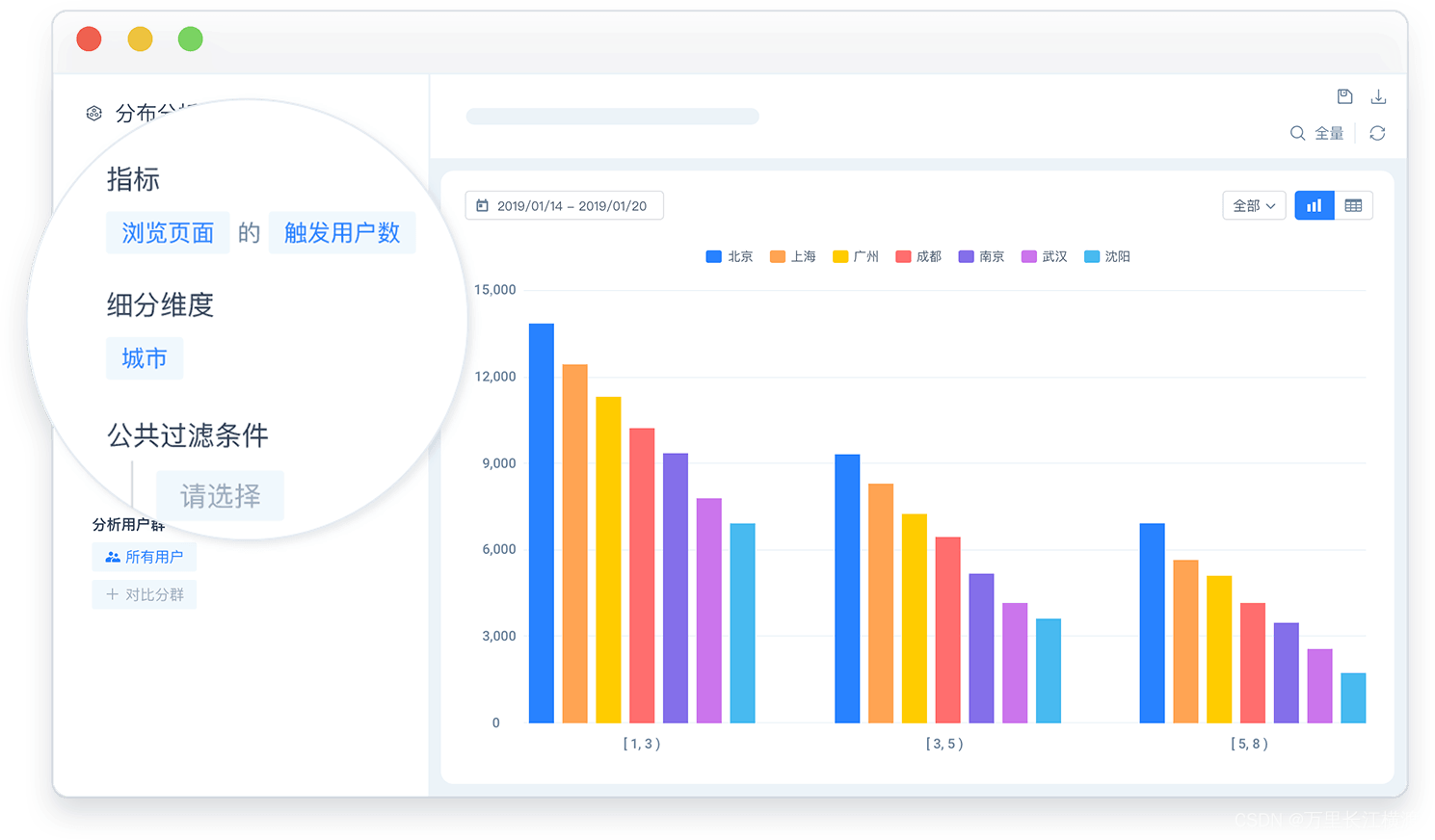
常见的九种大数据分析模型
常见的9种大数据分析模型分别为: 事件分析、 属性分析、 渠道分析、 Session分析、 留存分析、 归因分析、 漏斗分析、 路径分析、 分布分析 1、【事件分析】 事件分析,是指用户在 APP、网站等应用上发生的行为,即何人,何时&…...
技术的基本原理、特性、发展和应用)
射频识别(RFID)技术的基本原理、特性、发展和应用
何谓射频识别 随着高科技的蓬勃发展,智能化管理已经走进了人们的社会生活,一些门禁卡、第二代身份证、公交卡、超市的物品标签等,这些卡片正在改变人们的生活方式。其实秘密就在这些卡片都使用了射频识别技术,可以说射频识别已成…...

3.3 二维随机变量条件分布
学习目标: 要学习二维随机变量的条件分布,我可能会采取以下步骤: 复习边缘分布和联合分布:首先需要了解二维随机变量的边缘分布和联合分布的概念以及相应的公式。 复习条件概率:学习条件概率的定义和计算公式&#x…...

Kafka——概述、安装及命令行操作
文章目录一、概述1.1、定义1.2、如何运作?1.3、传统消息队列的应用场景1.4、消息队列的两种模式1.5、Kafka的基础架构二、安装(需要安装zookeeper)三、常用命令行操作3.1、主题命令行操作3.2、生产者命令行操作3.3、消费者命令行操作一、概述…...

怎么控制ERP企业管理系统开发的价格
企业资源规划(ERP)是一种广泛使用的商业软件系统,用于管理企业的各个方面,包括财务、供应链、客户关系、人力资源等等。开发一个适合企业的ERP系统可能是一项昂贵的任务,但控制ERP企业管理系统开发的价格是可行的。以下…...
我在“Now In Android”中学到的 9 件事
我在“Now In Android”中学到的 9 件事 Now in Android是一款功能齐全的 Android 应用程序,完全使用 Kotlin 和 Jetpack Compose 构建。它遵循 Android 设计和开发最佳实践,旨在为开发人员提供有用的参考。 https://github.com/android/nowinandroid UI…...
ChatGPT宝藏插件丨装上之后,上网、语音聊天、一键分享对话……简直让你爽到起飞!
今天分享4个让你的 ChatGPT 功能更强大的浏览器插件,装上就能用,每一个都是精挑细选。 1. WebChatGPT 很多小伙伴在用 ChatGPT查阅信息时,发现它有一个致命的问题: ChatGPT的知识库全部截止到 2021年9月,正常情况下…...
私有句柄表
私有句柄表 实验环境 win7 x86 什么是私有句柄表? 私有句柄表是操作系统内部的一种数据结构,用于存储一个进程所拥有的句柄(或称为句柄对象)的信息。在操作系统中,句柄是一个标识符,用于唯一标识一个对…...

Vue——类与样式绑定
目录 Class 与 Style 绑定 绑定 HTML class 绑定对象 绑定数组 在组件上使用 绑定内联样式 绑定对象 绑定数组 自动前缀 样式多值 Class 与 Style 绑定 数据绑定的一个常见需求场景是操纵元素的 CSS class 列表和内联样式。因为 class 和 styl…...

软考中项计算题总结
计算题在下午的考试属于重中之重,可以说得计算题得天下,先把计算题搞定,再看案例找错题,这2个是最容易得分的,所以对于进度、成本类的计算题一定要搞懂: 所属项目过程计算计算公式说明进度管理三点估算&am…...
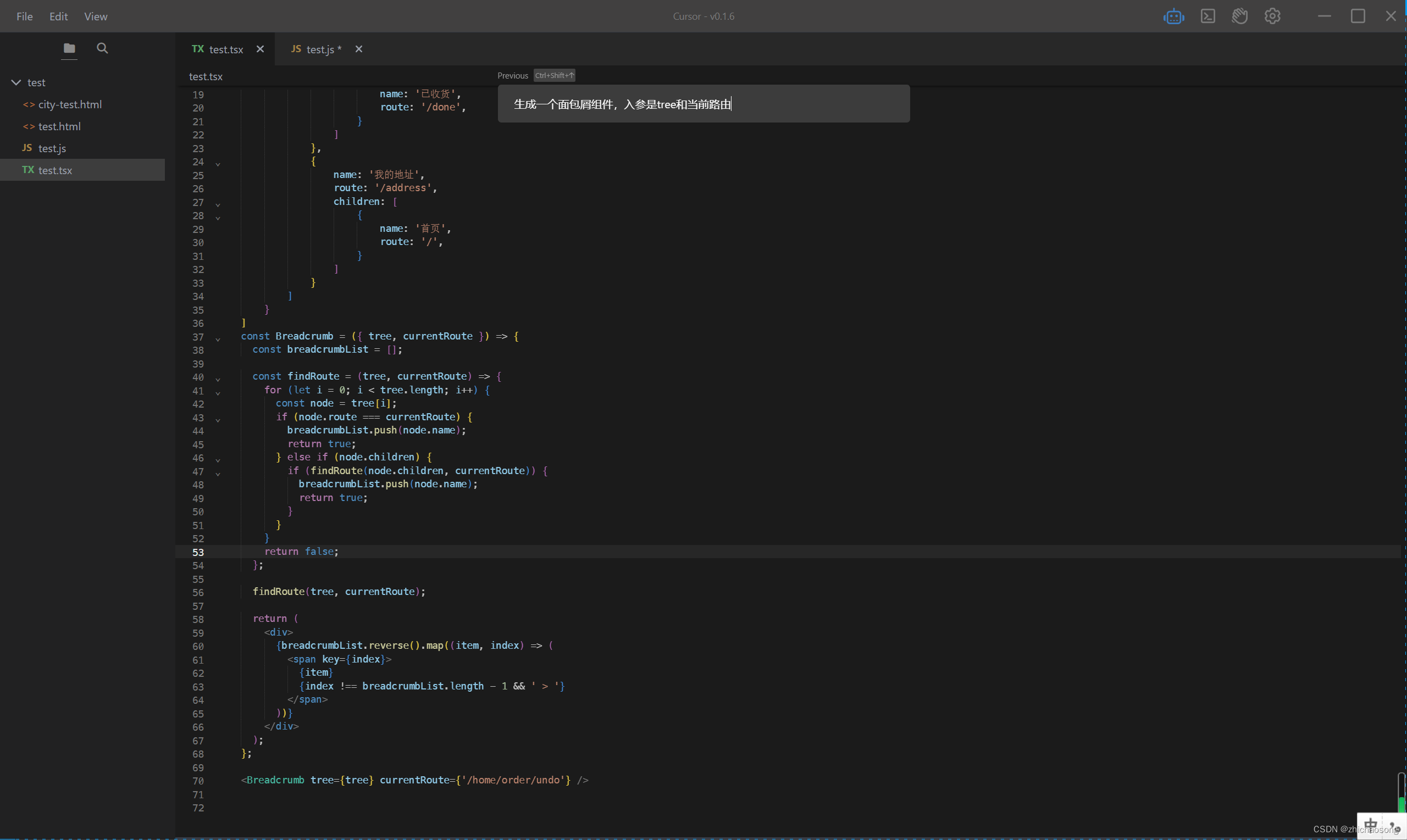
如何使用基于GPT-4的Cursor编辑器提升开发效率
程序员最恨两件事情:一是别人代码不写文档,二是要让自己写文档。随着 GPT-4 的到来这些都不是问题了,顺带可能连程序员都解决了。。。 之前一直觉得 AI 生成的代码也就写个面试题的水平,小打小闹,现在时代可变了。Curs…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
