在排序数组中查找元素的第一个和最后一个位置(二分查找进阶)
在写这个题目之前需要大家自行看一下我之前写的博客有关二分查找思想,如何判断什么时候使用二分查找以及边界值的确定:二分查找思想+力扣实例_徐憨憨!的博客-CSDN博客
题目:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置;如果数组中不存在目标值 target,返回 [-1, -1];你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题.
题目链接:力扣
思路分析:
1. 题目给出了在有序数组中查找目标元素target下标的位置且要求时间复杂度是O(logn),此时想到的就是利用二分查找;
2.目标元素target可能存在于数组中也可能不存在于数组中,需要分情况讨论,可以分成target在数组的左边,在数组的右边,和数组的内部:
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
3.当数组中有target这个元素时,需要分别求出target的左边界(即第一次出现的位置)和右边界(即最后一次出现的位置),又因为时间复杂度要求是O(logn),所以在找左右边界的时候依然采用二分查找的策略,只是判断条件和下标更新的时候需要稍作调整;
4.因为给出的区间是左闭右闭的,所以在while循环中的判断语句使用left <= right,当调出循环时,left一定大于right,所以得到的左右边界都是不包含target的.
寻找右边界:
//找右边界值private int findRightBorder(int[] nums, int target) {int left = 0;int right = nums.length - 1;int rightBorder = -2; //如果返回的rightBorder为-2说明没有查找到右边界while (left <= right) {int mid= left + ((right - left) / 2);//防止数据溢出if (nums[mid] > target) {//此时说明右边界一定在mid的左边right = middle - 1;} else { //nums[mid]=target时,说明右边界>=mid//nums[mid<target时,说明右边界>midleft = mid+ 1;rightBorder = left;}}return rightBorder;}
寻找左边界:
//找左边界值private int findLeftBorder(int[] nums, int target) {int left = 0;int right = nums.length - 1;int leftBorder = -2;//如果返回-2,说明没有找到左边界值while (left <= right) {int middle = left + ((right - left) / 2);//防止数据溢出if (nums[middle] >= target) { //当nums[mid]=target时,说明左边界<=mid//当nums[mid]>target时,说明左边界<midright = middle - 1;leftBorder = right;} else {//当nus[mid]<target时,说明左边界>midleft = middle + 1;}}return leftBorder;}主方法中:
public int[] searchRange(int[] nums, int target) {int leftBorder = findLeftBorder(nums, target);int rightBorder = findRightBorder(nums, target);//表示target在数组的左边和右边if (leftBorder == -2 || rightBorder == -2) return new int[]{-1, -1};//说明target在存在于数组内部if (rightBorder - leftBorder > 1) {//因为leftBorder和rightBorder都不包含边界值target//所以需要给leftBorder+1 rightBorder-1return new int[]{leftBorder + 1, rightBorder - 1};}return new int[]{-1, -1};}完整代码如下:
class Solution {public int[] searchRange(int[] nums, int target) {int leftBorder = findLeftBorder(nums, target);int rightBorder = findRightBorder(nums, target);//表示target在数组的左边和右边if (leftBorder == -2 || rightBorder == -2) return new int[]{-1, -1};//说明target在存在于数组内部if (rightBorder - leftBorder > 1) {//因为leftBorder和rightBorder都不包含边界值target//所以需要给leftBorder+1 rightBorder-1return new int[]{leftBorder + 1, rightBorder - 1};}return new int[]{-1, -1};}//找右边界值private int findRightBorder(int[] nums, int target) {int left = 0;int right = nums.length - 1;int rightBorder = -2; while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] > target) {right = middle - 1;} else { left = middle + 1;rightBorder = left;}}return rightBorder;}//找左边界值private int findLeftBorder(int[] nums, int target) {int left = 0;int right = nums.length - 1;int leftBorder = -2;while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] >= target) { right = middle - 1;leftBorder = right;} else {left = middle + 1;}}return leftBorder;}}相关文章:
)
在排序数组中查找元素的第一个和最后一个位置(二分查找进阶)
在写这个题目之前需要大家自行看一下我之前写的博客有关二分查找思想,如何判断什么时候使用二分查找以及边界值的确定:二分查找思想力扣实例_徐憨憨!的博客-CSDN博客 题目:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定…...
1 Nginx跨域配置
跨域问题在之前的单体架构开发中,其实是比较少见的问题,除非是需要接入第三方SDK时,才需要处理此问题。但随着现在前后端分离、分布式架构的流行,跨域问题也成为了每个Java开发必须要懂得解决的一个问题。 跨域问题产生的原因 产…...
ChatGTP如此强大,我们普通人如何利用它来赚钱?
我从效率提升的角度,分享了我这段时间看到的、用到的,以及思考的一些内容。 最近这段时间,我算是密集的学习。不得不说,优质的资料在推特和油管上特别多,看科技大佬的分享真是一种享受。 很多大神也会录制各种详细的…...
常见的九种大数据分析模型
常见的9种大数据分析模型分别为: 事件分析、 属性分析、 渠道分析、 Session分析、 留存分析、 归因分析、 漏斗分析、 路径分析、 分布分析 1、【事件分析】 事件分析,是指用户在 APP、网站等应用上发生的行为,即何人,何时&…...
技术的基本原理、特性、发展和应用)
射频识别(RFID)技术的基本原理、特性、发展和应用
何谓射频识别 随着高科技的蓬勃发展,智能化管理已经走进了人们的社会生活,一些门禁卡、第二代身份证、公交卡、超市的物品标签等,这些卡片正在改变人们的生活方式。其实秘密就在这些卡片都使用了射频识别技术,可以说射频识别已成…...

3.3 二维随机变量条件分布
学习目标: 要学习二维随机变量的条件分布,我可能会采取以下步骤: 复习边缘分布和联合分布:首先需要了解二维随机变量的边缘分布和联合分布的概念以及相应的公式。 复习条件概率:学习条件概率的定义和计算公式&#x…...

Kafka——概述、安装及命令行操作
文章目录一、概述1.1、定义1.2、如何运作?1.3、传统消息队列的应用场景1.4、消息队列的两种模式1.5、Kafka的基础架构二、安装(需要安装zookeeper)三、常用命令行操作3.1、主题命令行操作3.2、生产者命令行操作3.3、消费者命令行操作一、概述…...

怎么控制ERP企业管理系统开发的价格
企业资源规划(ERP)是一种广泛使用的商业软件系统,用于管理企业的各个方面,包括财务、供应链、客户关系、人力资源等等。开发一个适合企业的ERP系统可能是一项昂贵的任务,但控制ERP企业管理系统开发的价格是可行的。以下…...
我在“Now In Android”中学到的 9 件事
我在“Now In Android”中学到的 9 件事 Now in Android是一款功能齐全的 Android 应用程序,完全使用 Kotlin 和 Jetpack Compose 构建。它遵循 Android 设计和开发最佳实践,旨在为开发人员提供有用的参考。 https://github.com/android/nowinandroid UI…...
ChatGPT宝藏插件丨装上之后,上网、语音聊天、一键分享对话……简直让你爽到起飞!
今天分享4个让你的 ChatGPT 功能更强大的浏览器插件,装上就能用,每一个都是精挑细选。 1. WebChatGPT 很多小伙伴在用 ChatGPT查阅信息时,发现它有一个致命的问题: ChatGPT的知识库全部截止到 2021年9月,正常情况下…...
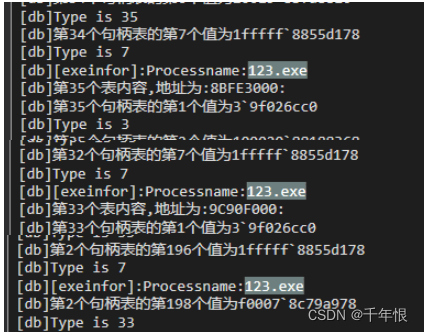
私有句柄表
私有句柄表 实验环境 win7 x86 什么是私有句柄表? 私有句柄表是操作系统内部的一种数据结构,用于存储一个进程所拥有的句柄(或称为句柄对象)的信息。在操作系统中,句柄是一个标识符,用于唯一标识一个对…...

Vue——类与样式绑定
目录 Class 与 Style 绑定 绑定 HTML class 绑定对象 绑定数组 在组件上使用 绑定内联样式 绑定对象 绑定数组 自动前缀 样式多值 Class 与 Style 绑定 数据绑定的一个常见需求场景是操纵元素的 CSS class 列表和内联样式。因为 class 和 styl…...

软考中项计算题总结
计算题在下午的考试属于重中之重,可以说得计算题得天下,先把计算题搞定,再看案例找错题,这2个是最容易得分的,所以对于进度、成本类的计算题一定要搞懂: 所属项目过程计算计算公式说明进度管理三点估算&am…...
如何使用基于GPT-4的Cursor编辑器提升开发效率
程序员最恨两件事情:一是别人代码不写文档,二是要让自己写文档。随着 GPT-4 的到来这些都不是问题了,顺带可能连程序员都解决了。。。 之前一直觉得 AI 生成的代码也就写个面试题的水平,小打小闹,现在时代可变了。Curs…...
压箱底教程分享,手把手教会你如何注册target账号和下单
喜欢套利的朋友肯定都认识target这个平台吧,它是美国热门的综合性海淘网站之一。东哥近日收到私信有朋友向我请教在注册target账号时遇到的一些问题,所以今天东哥想跟大家分享的就是就是target账号注册教程和下单流程,让也想注册target账号的…...
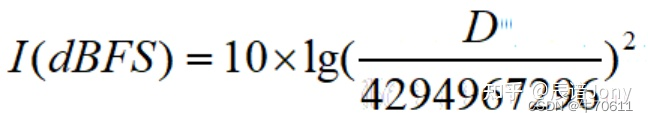
一次性搞懂dBSPL、dBm、dBu、dBV、dBFS的区别!
相信学习音乐制作的同学在混音阶段经常会碰到各种关于声音的单位,其中最具代表性的可能就是分贝家族的单位了,如dBSPL、dBm、dBu、dBV、dBFS等。 那么,这些单位分别表示什么,又有什么区别呢? 描述声音信号强弱的单位…...

漂亮实用的15个脑图模板,你知道哪些是AI做的吗?
对于很多第一次接触到思维导图的朋友,看到软件的时候往往找不到方向,不知道如何创作? 今天大家的好助手来了。 一是有大量的思维导图模板,大家看着模板做,慢慢就会做了。 二是ProcessOn 思维导图已经可以用AI 做思维…...

历代程序员都无法逃脱的诅咒 -- 低代码
1764年5月4日星期四 愤怒的纺织工人 纵火烧毁了哈格里夫斯的家 因为他发明的珍妮纺织机 让很多当地的手工纺织工人失业了 这也被认为是第一次工业革命的开端 由于事发的星期四 所以这一事件也被称作疯狂星期四 类似的变革 也一次次的出现在软件行业 他是历代程序员都无法逃脱的…...

14Exceptional Control Flow Exceptions and Process(异常控制流,异常和进程)
异常控制流 异常控制流出现的地方: 异常控制流(Exceptional Control Flow,ECF)是程序执行过程中由于某些特殊事件或条件而导致的控制流的改变。异常控制流通常出现在以下几种情况: 硬件异常和中断:硬件异…...

LeetCode - 两数之和
题目信息 源地址:两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
