3.3 二维随机变量条件分布
学习目标:
要学习二维随机变量的条件分布,我可能会采取以下步骤:
-
复习边缘分布和联合分布:首先需要了解二维随机变量的边缘分布和联合分布的概念以及相应的公式。
-
复习条件概率:学习条件概率的定义和计算公式,理解条件概率的含义和作用。
-
掌握条件分布的定义:理解条件分布的概念和定义,了解条件分布的性质和特点。
-
学习条件分布的计算方法:学习如何计算条件分布,包括离散型随机变量和连续型随机变量的条件分布。
-
练习例题:通过大量的例题来巩固所学知识,并掌握如何应用条件分布解决实际问题。
-
拓展应用:探究条件分布在其他领域中的应用,如机器学习中的贝叶斯分类器等。
在学习过程中,需要注意以下重点、难点和易错点:
-
熟练掌握边缘分布和联合分布的概念和公式,理解二维随机变量的含义和作用。
-
理解条件概率的概念和计算方法,能够熟练地计算条件概率。
-
了解条件分布的定义和性质,能够判断条件分布的类型并计算其概率密度或概率分布律。
-
注意离散型随机变量和连续型随机变量在条件分布中的区别,掌握它们的计算方法。
-
注意条件分布与边缘分布和联合分布之间的关系,理解它们之间的联系和作用。
-
在解决实际问题时,要注意问题的描述和条件的转换,避免出现计算错误。
-
多做练习,提高对条件分布的理解和应用能力。

我的理解:
离散型随机变量的条件分布指在给定另一随机变量的取值条件下,该随机变量的取值的概率分布。假设 X 和 Y是两个离散型随机变量,P(X=x,Y=y) 是它们的联合概率分布,则在给定 Y=y 的条件下,X的条件概率分布为:
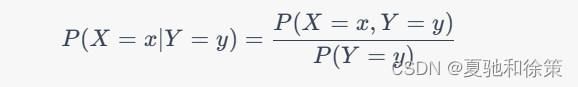
其中,P(Y=y)称为边缘概率分布。类似地,给定 X=x的条件下Y的条件概率分布为:
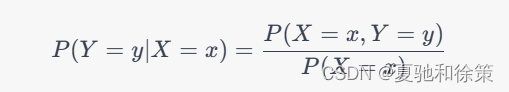
其中,P(X=x)也称为边缘概率分布。
需要注意的是,条件分布只有在 P(Y=y)>0或 P(X=x)>0 的条件下才有定义。



我的理解:
对于连续型二维随机变量 (X,Y),给定条件 Y=y下X的条件分布为:
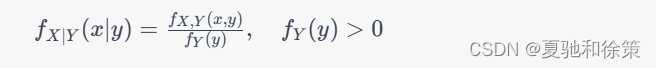
其中 f_{X,Y}(x,y)为 (X,Y)的联合概率密度函数,f_Y(y)为 Y的概率密度函数。
类似地,给定条件 X=x 下 Y 的条件分布为:
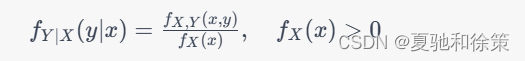
其中 f_X(x)为X的概率密度函数。
在实际应用中,我们常常需要求解一些与条件分布相关的问题,例如求解条件期望、条件方差、条件概率等等。对于这些问题,我们可以根据条件分布的定义,将其转化为单变量随机变量的问题来求解。
总结:
二维随机变量的条件分布是概率论中的重要概念之一。其重点在于理解条件概率的概念和公式,以及在不同类型的二维随机变量中如何求解条件分布。下面是一些可能的重点、难点和易错点的总结:
重点:
- 理解条件概率的概念和公式:条件概率是指在已知某些条件下,另一事件发生的概率。它的公式是 P(A|B) = P(A∩B) / P(B),其中 A∩B 表示事件 A 和事件 B 的交集。
- 理解条件分布的概念:条件分布是指在已知某些条件下,另一随机变量的分布。它的公式是 P(Y=y|X=x) = P(X=x,Y=y) / P(X=x),其中 X 和 Y 是两个随机变量。
- 熟练掌握边缘分布和联合分布的概念和计算方法:边缘分布是指一个随机变量的概率分布,而联合分布是指多个随机变量的概率分布。在求解条件分布时,需要用到这些概念和计算方法。
难点:
- 确定条件分布的类型:在不同的二维随机变量中,条件分布的类型有所不同,比如连续型二维随机变量的条件分布通常是概率密度函数,而离散型二维随机变量的条件分布通常是概率分布律。因此,需要针对不同类型的随机变量进行分类讨论。
- 掌握条件分布的计算方法:在求解条件分布时,需要根据条件概率的公式和边缘分布、联合分布的计算方法,确定条件分布的公式或计算步骤。这通常需要一定的数学技巧和思维灵活性。
- 确定条件变量的范围:在求解条件分布时,需要确定条件变量的取值范围,以便进行条件概率和条件分布的计算。如果条件变量的取值范围不确定或计算错误,可能会导致条件分布的计算错误。
易错点:
- 混淆条件概率和条件分布:有时候容易混淆条件概率和条件分布的概念和计算方法,导致计算错误。
- 忘记考虑条件变量的范围:在求解条件分布时,有时候会忘记考虑条件变量的取值范围,导致条件分布的计算错误。
- 求解边缘分布和联合分布时出错

相关文章:

3.3 二维随机变量条件分布
学习目标: 要学习二维随机变量的条件分布,我可能会采取以下步骤: 复习边缘分布和联合分布:首先需要了解二维随机变量的边缘分布和联合分布的概念以及相应的公式。 复习条件概率:学习条件概率的定义和计算公式&#x…...

Kafka——概述、安装及命令行操作
文章目录一、概述1.1、定义1.2、如何运作?1.3、传统消息队列的应用场景1.4、消息队列的两种模式1.5、Kafka的基础架构二、安装(需要安装zookeeper)三、常用命令行操作3.1、主题命令行操作3.2、生产者命令行操作3.3、消费者命令行操作一、概述…...

怎么控制ERP企业管理系统开发的价格
企业资源规划(ERP)是一种广泛使用的商业软件系统,用于管理企业的各个方面,包括财务、供应链、客户关系、人力资源等等。开发一个适合企业的ERP系统可能是一项昂贵的任务,但控制ERP企业管理系统开发的价格是可行的。以下…...
我在“Now In Android”中学到的 9 件事
我在“Now In Android”中学到的 9 件事 Now in Android是一款功能齐全的 Android 应用程序,完全使用 Kotlin 和 Jetpack Compose 构建。它遵循 Android 设计和开发最佳实践,旨在为开发人员提供有用的参考。 https://github.com/android/nowinandroid UI…...
ChatGPT宝藏插件丨装上之后,上网、语音聊天、一键分享对话……简直让你爽到起飞!
今天分享4个让你的 ChatGPT 功能更强大的浏览器插件,装上就能用,每一个都是精挑细选。 1. WebChatGPT 很多小伙伴在用 ChatGPT查阅信息时,发现它有一个致命的问题: ChatGPT的知识库全部截止到 2021年9月,正常情况下…...
私有句柄表
私有句柄表 实验环境 win7 x86 什么是私有句柄表? 私有句柄表是操作系统内部的一种数据结构,用于存储一个进程所拥有的句柄(或称为句柄对象)的信息。在操作系统中,句柄是一个标识符,用于唯一标识一个对…...

Vue——类与样式绑定
目录 Class 与 Style 绑定 绑定 HTML class 绑定对象 绑定数组 在组件上使用 绑定内联样式 绑定对象 绑定数组 自动前缀 样式多值 Class 与 Style 绑定 数据绑定的一个常见需求场景是操纵元素的 CSS class 列表和内联样式。因为 class 和 styl…...

软考中项计算题总结
计算题在下午的考试属于重中之重,可以说得计算题得天下,先把计算题搞定,再看案例找错题,这2个是最容易得分的,所以对于进度、成本类的计算题一定要搞懂: 所属项目过程计算计算公式说明进度管理三点估算&am…...
如何使用基于GPT-4的Cursor编辑器提升开发效率
程序员最恨两件事情:一是别人代码不写文档,二是要让自己写文档。随着 GPT-4 的到来这些都不是问题了,顺带可能连程序员都解决了。。。 之前一直觉得 AI 生成的代码也就写个面试题的水平,小打小闹,现在时代可变了。Curs…...
压箱底教程分享,手把手教会你如何注册target账号和下单
喜欢套利的朋友肯定都认识target这个平台吧,它是美国热门的综合性海淘网站之一。东哥近日收到私信有朋友向我请教在注册target账号时遇到的一些问题,所以今天东哥想跟大家分享的就是就是target账号注册教程和下单流程,让也想注册target账号的…...
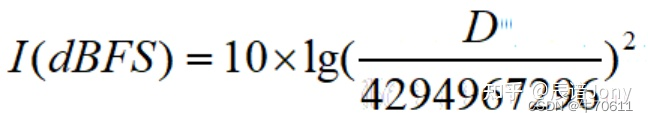
一次性搞懂dBSPL、dBm、dBu、dBV、dBFS的区别!
相信学习音乐制作的同学在混音阶段经常会碰到各种关于声音的单位,其中最具代表性的可能就是分贝家族的单位了,如dBSPL、dBm、dBu、dBV、dBFS等。 那么,这些单位分别表示什么,又有什么区别呢? 描述声音信号强弱的单位…...

漂亮实用的15个脑图模板,你知道哪些是AI做的吗?
对于很多第一次接触到思维导图的朋友,看到软件的时候往往找不到方向,不知道如何创作? 今天大家的好助手来了。 一是有大量的思维导图模板,大家看着模板做,慢慢就会做了。 二是ProcessOn 思维导图已经可以用AI 做思维…...

历代程序员都无法逃脱的诅咒 -- 低代码
1764年5月4日星期四 愤怒的纺织工人 纵火烧毁了哈格里夫斯的家 因为他发明的珍妮纺织机 让很多当地的手工纺织工人失业了 这也被认为是第一次工业革命的开端 由于事发的星期四 所以这一事件也被称作疯狂星期四 类似的变革 也一次次的出现在软件行业 他是历代程序员都无法逃脱的…...

14Exceptional Control Flow Exceptions and Process(异常控制流,异常和进程)
异常控制流 异常控制流出现的地方: 异常控制流(Exceptional Control Flow,ECF)是程序执行过程中由于某些特殊事件或条件而导致的控制流的改变。异常控制流通常出现在以下几种情况: 硬件异常和中断:硬件异…...

LeetCode - 两数之和
题目信息 源地址:两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不…...

Python 小型项目大全 31~35
三十一、猜数字 原文:http://inventwithpython.com/bigbookpython/project31.html 猜数字是初学者练习基本编程技术的经典游戏。在这个游戏中,电脑会想到一个介于 1 到 100 之间的随机数。玩家有 10 次机会猜出数字。每次猜中后,电脑会告诉玩…...

他又赚了一万美金
有一些学员真的挺能干的,收了一万刀,感到欣慰,毕竟在国外lead这条路,有很多人被骗,也有很多人赚钱。 但是大部分人跟着某一些所谓的大佬,最后自己却不动手操作。 从一开始怕跟我学习,到最后选…...

企业工程项目管理系统+spring cloud 系统管理+java 系统设置+二次开发
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

教你使用Apache搭建Http
Apache2默认采用的是80端口号,因此直接通过公网ip或域名就能访问。现实中,很多服务器本身就部署了许多其它服务,80端口号往往被占用,因此就需要将Apache2改成其它访问端口。 修改端口,首先需要修改/etc/apache2/ports…...
ZooKeeper+Kafka+ELK+Filebeat集群搭建实现大批量日志收集和展示
文章目录一、集群环境准备二、搭建 ZooKeeper 集群和配置三、搭建 Kafka 集群对接zk四、搭建 ES 集群和配置五、部署 Logstash 消费 Kafka数据写入至ES六、部署 Filebeat 收集日志七、安装 Kibana 展示日志信息一、集群环境准备 1.1 因为资源原因这里我就暂时先一台机器部署多…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

